从一道研究生入学考试试题的多种解法探讨积分学教学*

王 飞,南梦迪

(1.新疆农业大学 数理学院,新疆 乌鲁木齐 830052;2.江南大学 理学院,江苏 无锡 214122)

全国硕士研究生入学考试是我国的一项高级别的选拔性考试,已有许多学者对其命题进行了研究[1-6].曲线积分和曲面积分是高等数学中的难点,涉及曲线、曲面的定义,格林公式、高斯公式和斯托克斯公式,曲线、曲面积分的关系,曲线积分与路径的无关性,曲线、曲面积分转化为定积分或重积分等知识点,综合性强且计算量大,历年来考生在此考点的得分率都较低.本文以2022年全国研究生入学考试数学一的第二型曲线积分试题为例,对这类题的解法进行多角度的探讨,并结合多年的高等数学教学经验提出积分学教学方面的一些建议:深刻理解概念表达的物理意义;注意区分概念的共性与个性;构建知识网络结构图;加强对一题多解能力的训练.

1 试题及其解法

试题L是曲面Σ:4x2+y2+z2=1,x≥0,y≥0,z≥0的边界,曲面方向朝上,已知曲线L的方向和曲面的方向符合右手法则,求

I=∮L(yz2-cosz)dx+2xz2dy+(2xyz+xsinz)dz.

解法一由Stokes公式可得

由两类曲面积分的关系可得

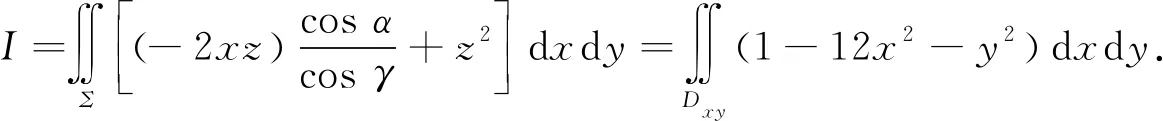
评注(1) 该解法先利用Stokes公式将第二型曲线积分化为第二型曲面积分,然后运用两类曲面积分的关系转化为仅对含变量x,y的曲面积分,再利用投影法转化为二重积分计算.求解过程涉及知识点较多,技巧性较高,计算量大,因而得分率比较低.

(2) 在利用Stokes公式将原积分化为第二型曲面积分后,也可以直接用投影法计算,具体过程如下.

记

Dyz={(y,z)|y2+z2≤1,y≥0,z≥0},Dxy={(x,y)|4x2+y2≤1,x≥0,y≥0},

则

由于

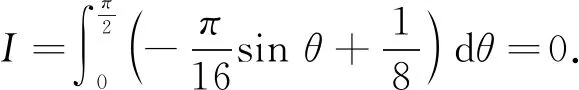
可见,这样求解计算量仍相当大.

解法二由Stokes公式可得

由两类曲面积分的关系,有

从而

由于

评注这里先用Stokes公式将第二型曲线积分化为第二型曲面积分,进一步再由两类曲面积分的关系转化为第一型曲面积分,最后化为二重积分.该解法的计算量也非常大.

解法三将L表为L=L1+L2+L3,其中

L1={(x,y,z)|x=0,y2+z2=1,y≥0,z≥0},方向从点(0,1,0)到(0,0,1);

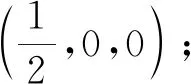
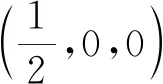
由第二型曲线积分的定义易知

故

补充曲线

L5={(x,y,z)|x=0,y=0,0≤z≤1},方向从点(0,0,0)到(0,0,1);

则由Green公式得

评注(1) 该解法借助第二型曲线积分的定义,将曲线方程代入被积函数化简,把较复杂的曲线积分转化为仅在L2上的积分,再利用Green公式快速得到了结果.该解法的计算量较小.(2) 注意到∮L2xz2dy=0,本题还可利用曲线积分与路径的无关性求解.

解法四由Stokes公式可得

记

Σ1={(x,y,z)|x=0,y2+z2≤1,y≥0,z≥0},

Σ2={(x,y,z)|y=0,z2+4x2≤1,z≥0,x≥0},

Σ3={(x,y,z)|z=0,4x2+y2≤1,x≥0,y≥0},

其中Σ1取后侧,Σ2取左侧,Σ3取下侧.

由第二型曲面积分的定义可知

于是由Gauss公式得

评注该解法先用Stokes公式将第二型曲线积分化为第二型曲面积分,然后由第二型曲面积分定义,通过补面法构造了封闭曲面,从而可利用Gauss公式快速求解.

2 对积分学教学的一些建议

结合上节给出的四种主要解法和教学经验,笔者对积分学教学提出一些建议.

2.1 注重理解概念的物理意义

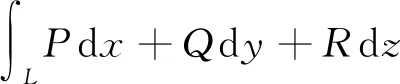
2.2 注意区分概念的共性与个性

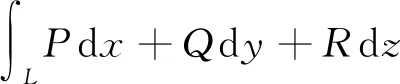
2.3 构建知识网络结构图

从解法一到解法四涉及的知识点有Green公式、Gauss公式和Stokes公式,曲线积分与曲面积分之间的关系,曲线积分和曲面积分转化为重积分等,综合性很强.因此,构建知识网络结构图十分重要.例如对于第二型空间曲线积分,我们可以构建如下的知识结构图.

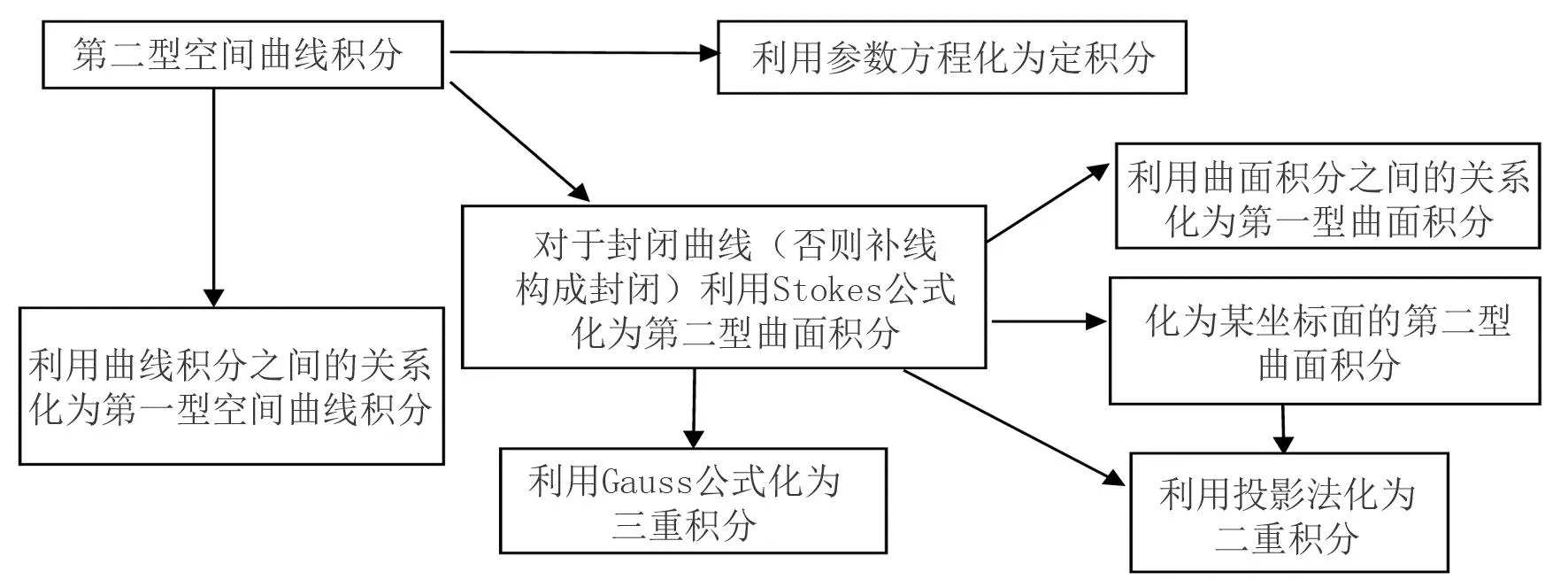
图1 第二型空间曲线积分计算的知识网络

2.4 注意一题多解能力的训练

一题多解可以启发学生从多角度分析问题,找准突破口,从而解决问题.这样的训练能使学生掌握更多知识,能提升学生多知识的运用能力,提升学生思维的品质.例如,学生进行本题多种解法的探究,可以熟悉曲线、曲面积分的知识点和技巧,获得发现简明解答方法的机会,提高解题能力与数学素养,增强创新意识,培养热爱探索的优良品质.