用Hirota双线性方法构造的高维sine-Gordon方程的新型精确解*

黎倍祯,毛 辉

(南宁师范大学 数学与统计学院, 广西 南宁 530100)

1971年Hirota提出一种用于求解各种非线性偏微分方程精确解的直接方法[1,2]:首先通过适当的函数变换将非线性偏微分方程化成由D算子来表示的双线性形式的方程,然后将函数的扰动展开式代入,在一定条件下将展开式在有限项处截断,由此得到具有指数形式的精确解.

非线性偏微分方程

uxx-utt=sinu

(1)

称为sine-Gordon方程.该方程可用于描述一维原子链模型、超导约瑟夫逊结、晶格错位的传播等诸多物理问题．另一方面,该方程所具有的纽结型孤立子、呼吸子等丰富的精确解类型可用于解释许多物理现象[3].因而sine-Gordon方程及其精确解受到了国内外学者的广泛关注[4,5].随着研究的深入,sine-Gordon方程的高维推广也进入了人们的视野[6,7,8],如二维sine-Gordon方程

uxx+uyy-utt=sinu

(2)

和一般的n维sine-Gordon方程

ux1x1+ux2x2+ux3x3+…+uxnxn-utt=sinu.

(3)

由于一维方程只能描述一维空间中的问题和规律, 因此对高维偏微分方程的研究无论在理论上还是在应用上都有重要的意义.目前关于高维sine-Gordon方程的精确解的研究尚不多,且结果多集中在纽结解的情况[6].本文利用Hirota双线性方法来构造二维sine-Gordon方程的新型精确解,然后将此类型的解推广到一般的n维sine-Gordon方程中.

1 Hirota双线性方法

设a(x,y,t)和b(x,y,t)是变量x,y和t的可微函数;Dx,Dy和Dt是微分算子;m,n和k为非负整数.双线性算子定义为

该算子有如下一些性质[2]:

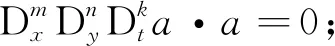
2 二维sine-Gordon方程的精确解

要用Hirota双线性方法来求解方程(2),需要先将方程(2)化为双线性形式.为此作函数变换

(4)

其中F和G为待定函数.对u求各阶导数,有

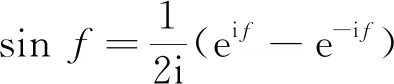
FG(F2-G2).

运用双线性算子可将上式整理为

于是可得到方程(2)的如下双线性形式:

(5)

为了得到方程(2)的精确解,假设F(x,y,t),G(x,y,t)具有形式

F(x,y,t)=a1eξ1+a2eξ2+a3eξ1+ξ2,G(x,y,t)=b0+b1eξ1+b2eξ2+b3eξ1+ξ2,

其中ξi=αix+βiy+γit,i=1,2.直接计算可得

F·G=a1b0eξ1+a1b1e2ξ1+a1b2eξ1+ξ2+a1b3e2ξ1+ξ2+a2b0eξ2+a2b1eξ1+ξ2+a2b2e2ξ2+a2b3eξ1+2ξ2+

a3b0eξ1+ξ2+a3b1e2ξ1+ξ2+a3b2eξ1+2ξ2+a3b3e2ξ1+2ξ2,

将上述结果代入(5)的第一式,比较函数的系数,有

e2ξ1:a1b1=0, e2ξ2:a2b2=0, e2ξ1+2ξ2:a3b3=0,

a1b2+a2b1+a3b0,

a1b3+a3b1,

a2b3+a3b2.

类似地,由(5)的第二式可得

通过求解上述方程组我们得到如下两种情况的解:

①a3≠0,b1≠0,b2≠0,a1=a2=b0=b3=0,且满足限制条件

此时方程(2)的解形如

u=4arctan e-x-y-t.

(6)

图1给出了该纽结解的三维图像以及剖面图.

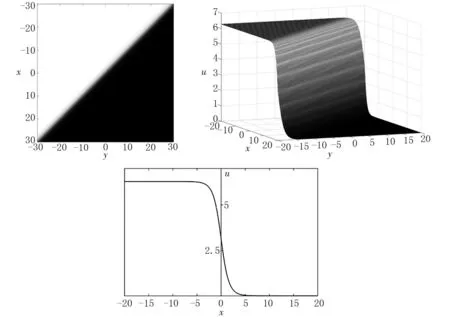
图1 方程(2)的纽结解(6)在t=0时刻的三维图像以及剖面图

②a1≠0,a2≠0,b0≠0,b3≠0,a3=b1=b2=0,且满足限制条件

此时方程(2)的解为

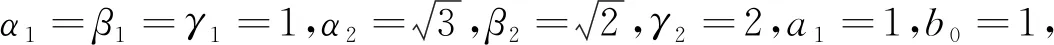
(7)

注意到存在使表达式(7)中分式部分的分子为正而分母为零的点,因此根据反正切函数的性质可知该解会在使分母为零的点出现“跳跃”现象.图2给出了该孤立子解的三维图像以及剖面图.

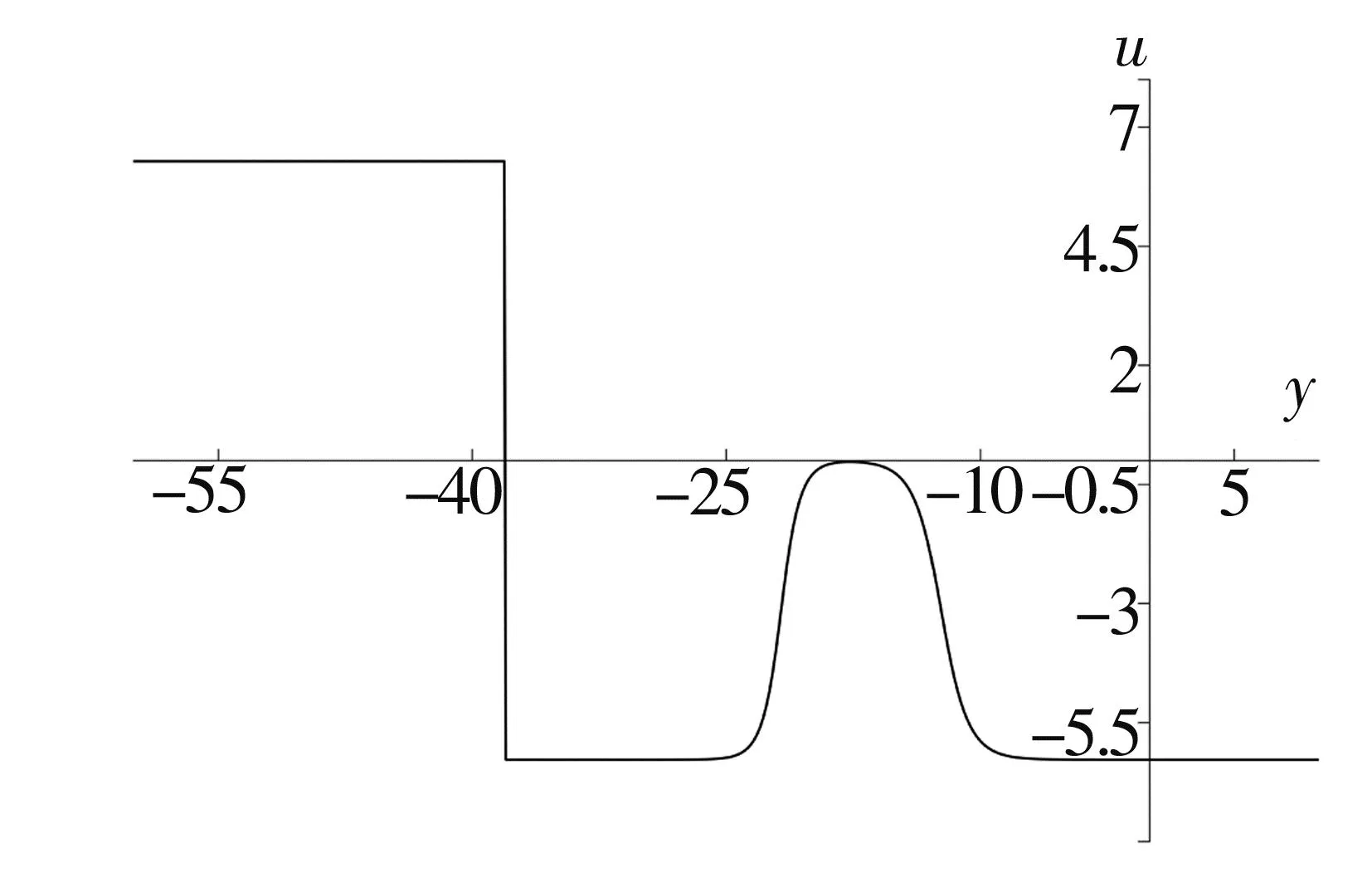
图2 方程(2)的孤立子型精确解(7)在t=0时刻的三维图像

3 n维sine-Gordon方程的孤立子型精确解

在上一节中我们利用Hirota双线性方法,通过对待定函数做拟设求出了方程(2)的两类精确解,其中孤立子类型的精确解与以往我们熟悉的有所不同.本节我们说明n维sine-Gordon方程(3)也有这两种类型的精确解.

定理1方程(3)有以下两类精确解:

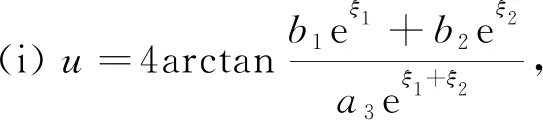
此时参数需满足限制条件

(ω11-ω21)2+(ω12-ω22)2+(ω13-ω23)2+…+(ω1n-ω2n)2-(υ1-υ2)2=0.

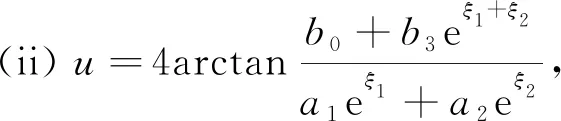
于是方程(3)化为

即

ux1x1+uyy-utt=sinu.

由上一节的结论可知方程(2)有如下解:

其中ξi=αix1+βiy+γit,i=1,2.此时参数需满足限制条件