阵元位置互质的线性阵列：阵列校正和波束形成

梁梦薇 何 劲 舒 汀 郁文贤

(上海交通大学电子信息与电气工程学院 上海 200240)

1 引言

自适应波束形成技术是传感器阵列信号处理的重要研究内容之一，被广泛应用于雷达、声呐、通信等领域，用于增强感兴趣信号(Signal-Of-Interest, SOI)和/或抑制干扰信号。近年来，国内外学者发展了大量稳健的自适应波束形成(Robust Adaptive Beamforming, RAB)算法，以解决非理想条件下的自适应波束形成问题。根据不同的设计准则，RAB算法主要分为以下几类：(1)基于对角加载的算法[1-3]；(2)基于特征空间的算法[4,5]；(3)基于高阶累积量的算法[6,7]；(4)基于最坏情况优化的算法[8,9]；(5)基于主瓣控制的算法[10,11]；(6)基于干扰噪声协方差矩阵(Interference-plus-Noise Covariance Matrix, INCM)重建的算法[12-14]。这些算法在阵列流形失配较小的情况下可以取得良好的性能。然而，实际应用中的天线阵列往往受到单元间互耦、通道幅相不一致等影响，使得实际与理想情况下的阵列流形存在较大失配，从而导致以上算法性能的急剧下降。

由于天线单元间的互耦与单元间距成反比，近年来提出的嵌套阵列[15,16]和互质阵列[17-19]等稀疏阵列结构可以有效地降低天线单元间的互耦影响。但是，考虑到嵌套阵列的第一级子阵的单元间距定义为半波长，互质阵列在阵列规模较小时的单元间距也较小，实际使用中的嵌套阵列和互质阵列仍然会受到天线单元间互耦的影响。为了进一步降低天线间互耦对阵列系统性能的影响，文献[20]中提出了阵元位置互质的线性阵列(Coprime Location Arrays,CLA)结构。与经典稀疏阵列相比，CLA具有以下两点性质和优势：(1)CLA任意阵元间距可不受半波长限制，可通过灵活设置阵元间距形成完全稀疏的阵列，从而可以将互耦效应降低至可忽略的水平；(2)由于不存在结构约束，所以相同阵元个数时，CLA可具有更大的阵列孔径，理论上可获得更高的测角精度。

CLA阵列校正本质上属于阵列校正问题。在过去十几年中，学者提出许多有效的阵列校正的方法，这些方法大致可以分为自校正方法和有源校正方法两类。自校正算法通过优化算法实时完成信号源方向和阵列误差联合估计，但通常需要较大的运算量；有源校正方法需要布设方向信息精确已知的辅助信号源，计算量较小，但对辅助信号源要求很高。而同时干扰定位与阵列校正(Simultaneous Interference Localization and Array Calibration,SILAC)技术[21]既不需要复杂的优化过程，也不需要设置辅助信号源。但这种算法基于阵元间距不大于半波长的线性阵列，未考虑校准子阵存在稀疏性时可能造成的相位模糊问题。根据定义，CLA属于完全稀疏阵列(阵列中任意两个阵元的间距均大于半波长)，CLA阵列校正的主要挑战是如何克服阵列稀疏性造成的相位模糊问题。由于CLA的概念是近期在文献[20]提出的，目前尚未有关于CLA阵列校正的相关工作报道。

本文从理论上证明了对于CLA，任意包含Lc≥3个阵元的子阵，其导向矢量均与信号角度构成一对一的映射关系。针对CLA中部分天线单元存在通道幅相不一致的情况，本文提出一种基于同时干扰定位与阵列校正技术的干扰噪声协方差矩阵重建波束形成方法：CLA-SILAC-INCM算法，来研究CLA的阵列校正和波束形成问题。算法思路概述如下：首先，定义两个4阶累积量矩阵并构造一矩阵束；其次，通过该矩阵束广义特征值得到一组高精度但模糊的干扰源角度估计值；随后，对每个模糊的角度值，计算得到与其对应的阵列误差矢量估计；然后，从理论上证明了当CLA中包含Lc≥3个完全校准的单元时，这两组模糊估计(干扰源角度估计和阵列误差矢量估计)可以彼此解模糊，从而得到高精度无模糊的干扰源定位和阵列校正；最后，利用SILAC的结果，完成INCM的重建和最优波束形成权向量的构造。CLA-SILAC-INCM算法无需积分/求和、优化等运算，且具有比其他常用算法更好的性能，尤其是信噪比接近干噪比时，性能优势更为明显。

文中的符号使用说明如下。斜体字母表示变量，斜体加粗的大写字母和小写字母分别表示矩阵和向量，I表示单位矩阵，0表示零矩阵或零向量，1表示元素均为1的列向量。[.]T、[.]*、[.]H分别表示转置、复共轭和共轭转置运算，[.]†表示伪逆运算，diag[.]表示以括号中的元素为主对角线元素构成的对角矩阵。 E [.]表示求数学期望。

2 模型与问题描述

考虑一个由L个天线单元组成的线性阵列，第一个天线单元为坐标原点，第l个天线单元的坐标dl=ml×λ/2, l = 2, 3, ···, L，λ为信号波长。若对任意l1, l2∈[2,L]，ml1与ml2互质，则该阵列为阵元位置互质的线性阵列，即CLA。有K ＜ L个远场窄带信号，分别从θk∈[- π/2, π/2]方向入射到阵列上。不失一般性，令第K个信号为期望信号，剩余K - 1个信号为干扰信号。阵列接收信号模型如图1所示。

图1 阵列的信号接收示意图

在时刻t，阵列接收信号可以表示为

其中，A=[a1,a2, ···,aK-1,aK]为阵列流形矩阵，ak=a(θk),k = 1, 2, ···, K - 1，为干扰信号的导向矢量；aK=a(θK)为期望信号的导向矢量，为与干扰信号导向矢量进行区别，通常将aK记为as，θK记为θs。s(t) = [s1(t), s2(t), ···, sK(t)]T为信号矢量。n(t)表示噪声矢量，xs(t) =assK(t)表示期望信号分量，表示干扰信号分量。对于完全校正的阵列，入射方向为θ的信号的导向矢量为

若阵列没有完全校正，接收通道间会存在幅度-相位不一致性。此时，接收信号修正为

式中，G= diag[g],g= [g1, g2, ···, gL]T表示阵列误差矢量，该矢量与入射信号方向无关，gl为复数，其模和幅角分别表示第l个接收通道的幅度误差和相位误差，若该接收通道已校正，则gl= 1。B=GA表示考虑接收通道幅相误差后的阵列流形矩阵。

波束形成的目标是设计权向量w= [w1, w2, ···,wL]T，使得输出信号干扰噪声比(Signal-to-Interference plus-Noise Ratio, SINR)最大。其中最常用的一种算法是最小方差无失真响应(Minimum Variance Distortionless Response, MVDR) 波束形成器，最优权向量表示为

本文的目标是：(1) 估计干扰源方向θk, k = 1,2, ···, K - 1和阵列误差矢量g，实现干扰源定位和阵列校正；(2) 精确重建干扰噪声协方差矩阵Ri+n和期望信号导向矢量bs，实现最优波束形成权向量的估计。本文后续算法的发展基于以下假设：

(a)信号到达方向互不相等，即当k1̸=k2时，θk1̸=θk2，且干扰信号在期望信号的主瓣波束之外。

(b)信号源s1(t), s2(t), ···, sK(t)是相互独立的非高斯信号。

(c)噪声假设为加性复高斯白噪声，与期望信号和干扰信号间统计独立。

(d)信号总个数K已通过预处理方法，如信息论方法[22]、平滑秩序列法[23]、盖式圆方法[24]、正则相关方法[25]等正确估计。

(e)已校正阵元的序号i1, i2, ···, iLc及个数Lc明确已知。

3 同时干扰源定位与阵列校正

当天线阵列间存在通道幅相不一致性时，会因导向矢量失配造成参数估计精度降低，波束形成性能变差。为对阵列进行校正，本节提出一种针对CLA的同时干扰源定位与阵列校正算法。该算法包含3个主要步骤：首先，构造1个4阶累积量矩阵束，通过计算矩阵束的广义特征值得到一组高精度但模糊的干扰源角度估计值；随后，对每个模糊的角度估计值，计算得到与其对应的阵列误差矢量估计；最后，通过解模糊处理得到高精度且无模糊的干扰源角度和阵列误差矢量估计。

为了更好地理解算法的核心思想，首先给出累积量的定义。累积量衡量了任意随机变量偏离正态(高斯)分布的程度，高斯随机过程大于2阶的累积量均为零。根据中心极限定理，阵列接收信号中的噪声为随机的，可以建模为高斯白噪声。而期望信号往往是确定性的，具有非高斯特性。因此，使用高阶累积量可以自动抑制高斯噪声并提取出有用的非高斯信号。此外，高阶累积量具有过程相位可检测性[26]，可保留接收信号中的相位信息，因此，使用累积量可以提取到干扰源的位置(角度)信息。本文算法基于4阶累积量来发展，信号xm(t), xn(t),xp(t), xq(t)的4阶累积量定义为[27]

其中，xl(t)表示x(t)中的第l个元素，将xl(t)简写为xl。假设第1个阵元和第l个阵元已校正，式(5)中令m=n=1,p,q=1,2,...,L，可以得到一个L×L维矩阵C1，表示为第1个天线单元对应的虚拟子阵的4 阶累积量矩阵。同样，令m=l,n=1,p,q=1,2,...,L，得到另一个L×L维矩阵Cl，表示为第l个天线单元对应的4阶累积量矩阵。由于s1(t),s2(t), ···, sK(t)彼此独立，根据文献[27]中累积量的性质推导出

3.1 信号方向的模糊估计

利用累积量矩阵C1和Cl可以构造矩阵束C1-zCl，其中z表示一复数。根据式(6)和式(7)可以推断出该矩阵束的广义特征值为Pl的所有对角元素。因此，可以通过使用ESPRIT算法[28]的思想求解上述矩阵束问题来获得Pl和B的估计。算法可通过对矩阵C=进行奇异值分解实现，具体描述如下。对C进行奇异值分解，得到K个主左奇异矢量(与K个较大奇异值对应的奇异矢量)，记为u1,u2, ···,uK。这些左奇异矢量共同构成信号子空间Us= [u1,u2, ···,uK]，且满足

其中，T表示一K×K维非奇异矩阵。令U1和Ul分别表示Us的前L列和后L列，可以得到U1=BT，Ul=BPlT。进一步计算可以得到Ul=U1T-1PlT，利用此式可以得到

根据式(9)，矩阵D的特征值和特征矢量分别为矩阵Pl和矩阵T的估计值。在得到T的估计之后，利用式(8)，可以得到矩阵B的估计。

3.2 阵列误差矢量的模糊估计

矢量bk可以表示成

根据式(12)，可以得到一组模糊的阵列误差矢量估计，表示为

其中，n的取值范围与式(10)中的定义相同。

3.3 解模糊处理

同时干扰源定位与阵列校正的最后一步是对得到信号方向的模糊估计和阵列误差矢量的模糊估计进行解模糊处理。为推导解模糊算法，先给出以下定理。

定理1对CLA，正确解模糊的充分条件是已校正天线单元个数Lc≥3。

首先证明，对于CLA，当Lc≥3时，任取Lc-1个天线单元与第一个天线单元构成Lc元子阵，其导向矢量不存在模糊。采用反证法证明。不妨设任意Lc元子阵的天线单元在C L A 中的序号为1,i2,...,iLc，假设存在θ1̸=θ2使得该子阵上的导向矢量相同，即

可以推出

对k = 1, 2, ···, K - 1依次进行以上处理，可估计出所有干扰信号的来波方向。在此基础上建立方程

4 波束形成权向量设计

通过第3节的分析，得到了干扰源方向和阵列误差矢量的估计。本节在此基础上，利用校正后的阵列导向矢量重建干扰噪声协方差矩阵，并设计波束形成权向量。

基于噪声与干扰信号相互独立这一假设，可以得到

在得到干扰信号功率和噪声功率的估计后，可以重建INCM为

利用3.3节得到的阵列误差矢量估计，可以重构SOI导向矢量为

综合以上分析，可以设计波束形成算法的权向量为

提出的算法与其他相关算法相比，具有以下优势：(1)对阵列误差进行了校正，可以更精准地实现对干扰源的定位；(2)对阵列误差进行补偿后，利用校正后的干扰信号导向矢量代替其他相关算法中使用的理想情况下的导向矢量，能够精确重建干扰噪声协方差矩阵，降低了阵列流形失配对波束形成算法造成的性能损失；(3)在重构干扰噪声协方差矩阵时，所提算法无需积分、求和、优化等运算，计算复杂度低。

5 仿真分析

本节将通过计算机仿真对提出算法的性能进行分析。假设CLA是由10个天线单元组成的部分校正阵列，ml从l = 2开始取相邻质数，m1取0，第1, 2,8, 10个天线单元为已校正阵元。考虑空间中有3个信号，第1个信号和第2个信号为干扰信号，分别从θ1=35°和θ2=-25°方向入射到阵列上，干噪比(Interference-to-Noise Ratio, INR)设置为30 dB，第3个信号为期望信号，从θs=10°方向入射到阵列上。考虑噪声为零均值的复高斯白噪声，归一化功率为1。采样数设置为200，除图2外，本节所有结果图上的点均通过200次独立蒙特卡罗模拟获得。

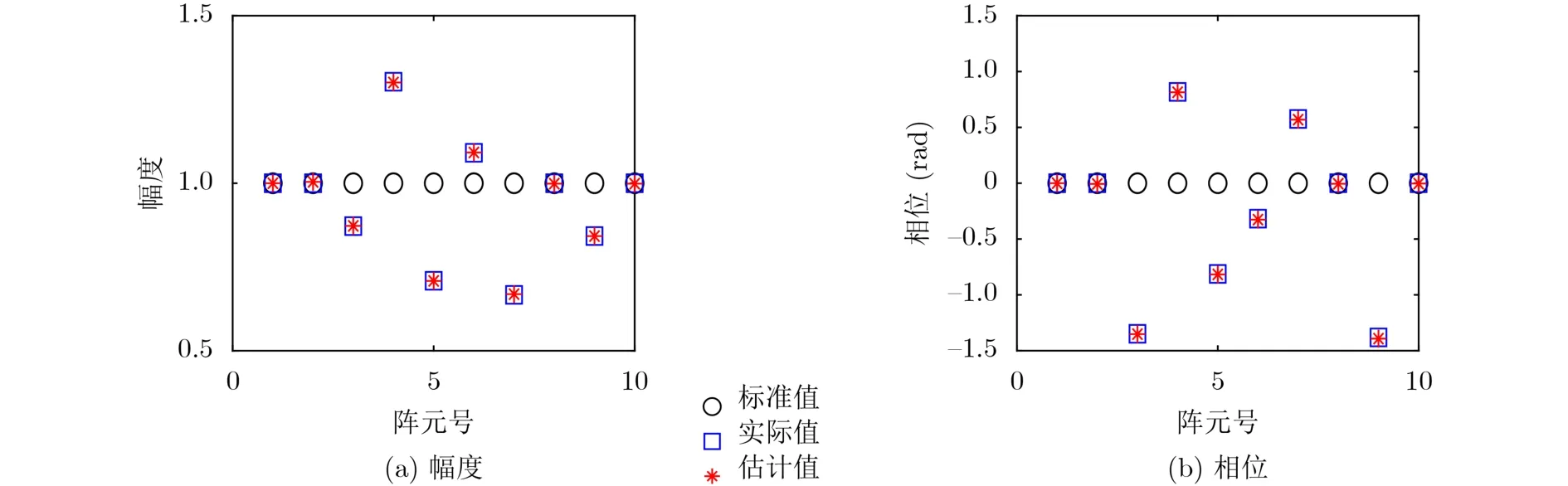
图2 CLA各天线单元幅度和相位的标准值、实际值和估计值

为了对比分析CLA-SILAC-INCM算法的性能，将其与采样矩阵求逆(Sample Matrix Inversion, SMI)算法[29]、对角加载SMI(Diagonal Loading SMI, LSMI)算法[1]、特征空间分解(Eigen-Space Decomposition, ESD)算法[4]、最差情况下性能优化(the Worst-Case Performance Optimization, WCPO)算法[8]、INCM-INT(the INCM reconstruction beamformer using INTegral)算法[12]、INCM-SPE(the INCM reconstruction beamformer using Simplified Power Estimation)算法[13]、INCM-RMT(the INCM reconstruction beamformer using the Random Matrix Theory)算法[14]的性能进行比较。其中LSMI算法中的加载因子设置为噪声功率的2倍，WCPO算法中失配因子的上界设置为阵元数的0.3倍，并使用MATLAB中的CVX软件包来求解优化问题，INCM-INT算法中期望信号所在方向覆盖的角度范围设置为Θ=[θs-5°,θs+5°]，则对应的干扰信号方向所在区间为Θ¯ =[-90°,θs-5°)∪(θs+5°,90°]，网格间隔设置为0.1°。为了评估波束形成性能，将最优波束形成器的性能也绘制在图中作为参考。

5.1 阵列校正性能

在理想条件下，测量通道不存在幅相误差，g=1，此时gl的幅度和相位分别为各阵元幅度和相位的标准值。实际应用中，阵列天线会存在通道不一致性，为了验证提出算法对阵列校正的有效性，在仿真实验中用提出算法估计阵元的实际幅度和相位。假设阵列幅度误差和相位误差服从相互独立的均匀分布，从均匀分布U(0.5,1.5)和U(- π/2, π/2)中产生随机数分别作为未校正阵元幅度和相位的实际值，第1, 2, 8, 10个天线单元为已校正阵元，g1=g2=g8=g10=1。空间中存在3个远场窄带信号，分别从35°,-25°,10°方向入射到阵列上，且3个信号与噪声的功率比SNR均为30 dB。采样数设置为200。图2绘制了各阵元幅度和相位的标准值、实际值和提出算法计算得到的估计值。可以看到，当CLA的阵元存在随机的幅度和相位误差时，提出的算法能够正确估计这些误差，从而实现阵列校正。

5.2 阵列完全校正时的性能

考虑阵列完全校正的情况，此时不存在导向矢量失配，即G=I。图3给出了不同算法的输出SINR随输入SNR的变化关系曲线。可以看出，当SNR较小时，除ESD算法外，其他算法都能近似达到最优算法的性能。而当SNR较大时，SMI, LSMI,WCPO算法的性能都有较大程度的损失。ESD算法在SNR大于-10 dB小于10 dB时性能良好，而SNR过小或过大时性能都较差。由于不存在导向矢量失配，所以基于协方差矩阵重建的INCM-INT,INCM-SPE, INCM-RMT和提出的算法均能有效消除期望信号分量，精确重建Rˆi+n，所以4种算法的形成性能几乎相同，能在整个SNR范围内近似达到最优性能。

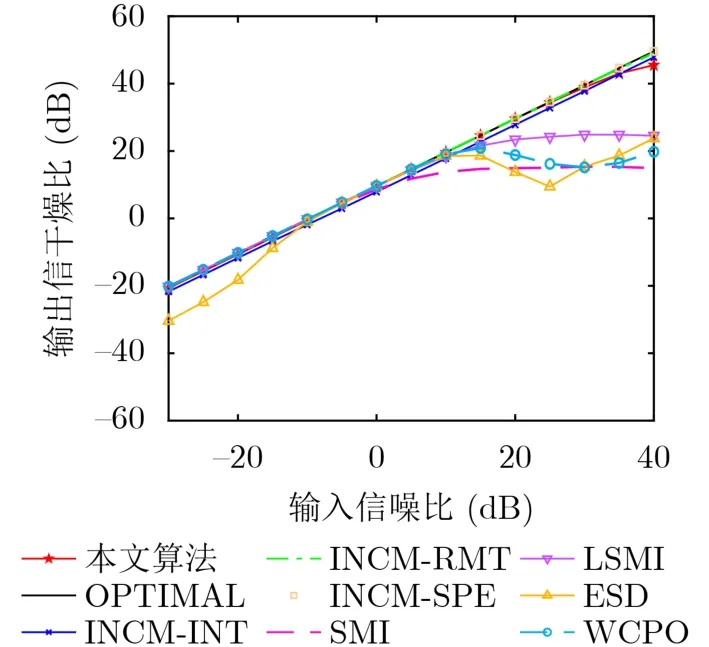
图3 阵列完全校正时的波束形成

5.3 存在方向误差时的性能

考虑阵列存在δθ的方向失配，这种失配可以是由于天线没有指向δθ=0°导致的。对于从θ方向入射的信号，阵列方向失配导致它看上去是从θ+δθ方向入射的，所以在第l个天线单元上产生一个固定的相位失配e-j2πdℓsinδθ/λ。对部分校正阵列，仿真中假设方向误差只出现在未校正的天线单元上。

假设阵列方向失配δθ=2°，不同算法的输出SINR性能如图4所示。由于存在导向矢量失配，所以提出的算法外的其他算法都出现性能损失，尤其在SNR较高时性能损失明显，其中INCM-SPE算法无法对部分校正的CLA阵列做波束形成，故未画出。INCM-INT算法重建INCM时依赖于完全校正的导向矢量，所以当阵列存在失配时，INCMINT算法有严重的性能损失。ESD算法将假设的导向矢量向样本的信号加干扰子空间做了投影，一定程度上降低了失配对波束形成性能的影响。提出的算法能够对阵列失配进行校正，故在存在阵列方向失配时能保持良好的波束形成性能。当SNR小于INR时，提出算法的性能非常接近最优性能，性能差距不超过0.5 dB；当SNR大于INR时，提出算法的性能较最优性能略有降低。

图4 阵列存在方向误差时的波束形成

5.4 阵列存在随机幅度和相位误差时的性能

考虑未校正阵元上存在随机的幅度和相位误差。假设幅度误差和相位误差分别服从[-0.1,0.1]和[- π/2, π/2]上的均匀分布。图5给出了不同算法的输出SINR性能，结果与5.3节中阵列存在方向误差时的结果相似，提出算法的性能依旧接近最优性能，具有很高的鲁棒性。

图5 存在随机幅度相位误差时波束形成

5.5 复杂环境下的波束形成性能

信号在复杂的环境中传播时可能会发生散射、波前失真等现象，期望信号的方向也可能发生失配。这一小节比较以下3种情况下算法的性能：(1)期望信号波达方向失配，假定的期望信号方向=8°，实际的期望信号方向θs=10°；(2)期望信号存在相干局部散射，此时实际的导向矢量为=as+其中{ψp,p=1,2,3,4}由独立同分布的高斯随机过程N(θs,1°)产生，{ϕp,p=1,2,3,4}是[0,2 π]之间的独立均匀分布随机数；(3) 期望信号存在波前失真，假设每一次蒙特卡罗实验中，期望信号波前的相位增量畸变独立地从高斯随机过程N(0,0.042rad)中产生。

使用5.4节中的CLA阵列，各种算法的SINR结果如图6所示。在期望信号存在方向失配时，提出算法的波束形成性能略有损失，较最优性能下降3 dB左右，但仍明显优于其他波束形成算法。当期望信号存在相干局部散射时，提出算法的波束形成性能在SNR大于INR时出现较明显损失，但与其他波束形成算法相比仍有明显优势。当期望信号存在波前失真时，提出算法的波束形成性能几乎没有损失，依旧能很好地接近最优性能。因此，提出的算法在复杂的环境中仍十分有效，具有很好的鲁棒性。

图6 复杂环境下的波束形成

5.6 雷达目标探测中的应用

为进一步评估算法在实际应用中的性能，给出了CLA-SILAC-INCM算法在雷达目标探测中的应用实例。假设一X波段阵列雷达包含10个接收通道，接收天线按CLA布置，各天线的坐标分别为[0,2,3,5, 7,11,13,17,19,23]×λ/2，其中第1, 2, 8,10个通道完全校正，其他通道存在幅相误差，复增益分别为g3=1.2e-j25π/180,g4=0.9ej5π/180,g5=1.05e-j60π/180,g6= 1.09ej15π/180,g7= 0.95ej75π/180,g9=0.92e-j45π/180。雷达为连续波体制，中心频率为10 GHz，采样频率为51.2 kHz，采样点数为512，相参处理时间为0.01 s。计算得到该雷达的最大无模糊径向速度为384 m/s，速度分辨率为1.5 m/s。假设空间内θs= 10°方向有一个20 dB的目标信号，θi= [-20°,30°]两方向有两个50 dB的干扰信号，目标信号和干扰信号独立且均为非高斯信号，目标径向速度为90 m/s。考虑系统在接收信号时产生功率为1的零均值高斯白噪声。

当波束形成权向量为w=as时(静态加权)，多普勒图如图7(a)所示，很明显目标信号完全淹没在干扰信号中。当使用提出的CLA-SILAC-INCM波束形成算法时，多普勒图如图7(b)所示，目标被成功检测出来，并且峰值对应的速度90.9276 m/s为目标的估计速度，估计误差在一个速度分辨单元内。

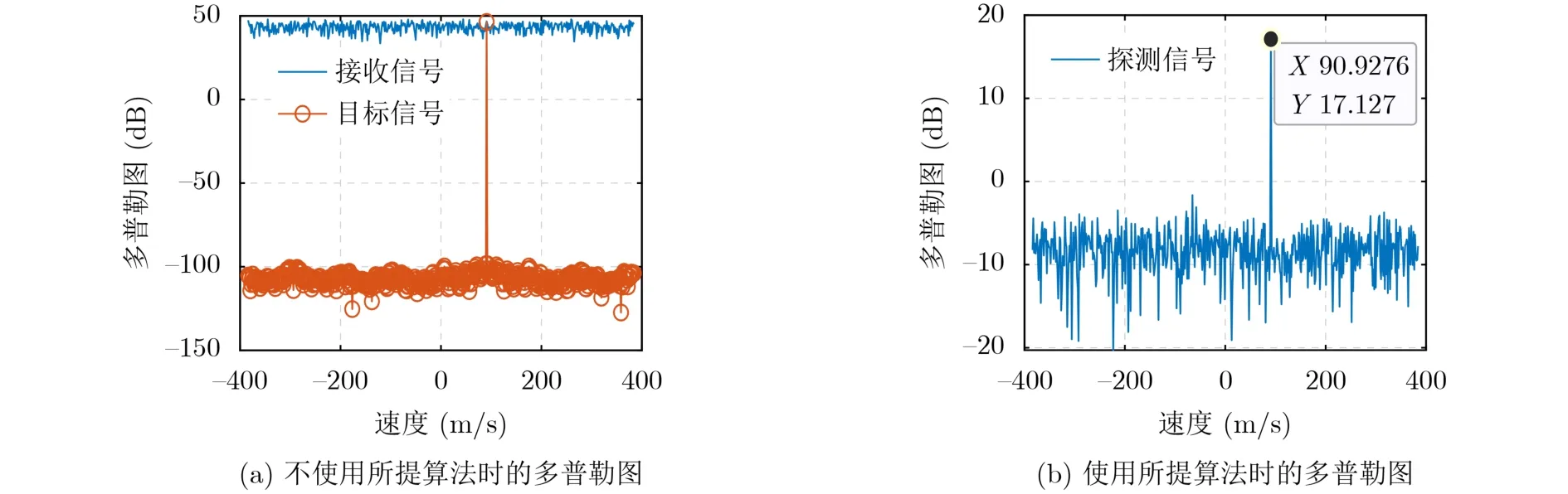
图7 目标探测多普勒图

6 结束语

本文针对部分校正的CLA，提出了一种有效的阵列误差校正和波束形成算法。文章在理论上证明了当CLA包含有Lc≥3个完全校准的天线单元时，使用SILAC技术可以高精度无模糊地实现干扰源方向和阵列天线幅相误差估计，并在此基础上完成INCM重建和波束形成最优权向量构造。针对大量场景进行的仿真试验结果表明，提出的CLA-SILACINCM算法具有比其他常用算法更好的性能，显示出良好的鲁棒性。