基于不确定区域的水下纯方位目标跟踪方案

李海鹏 聂朝阳

(哈尔滨工程大学青岛创新发展基地 青岛 266000)

(青岛哈尔滨工程大学创新发展中心 青岛 266000)

1 引言

水下被动目标跟踪技术一直以来是科研的热门方向，广泛应用于军事领域。在水下复杂环境中量测数据是非常有限的，目标方位几乎是唯一可靠的参数，融合目标方位信息对目标实施跟踪估计的纯方位目标运动分析技术(Bearing-Only Tracking Motion Analysis, BOTMA)成为水下被动目标跟踪的重要分支[1-3]，目前该技术仍面临众多困难，一是水下环境复杂多变，目标在未知因素较多的海洋环境中难以建立目标模型；二是水下被动传感器精度不高，导致量测精度及量测信息质量较差；三是水下采样成本较高，难以连续获取稳定采样信息。由上述困难衍生出新问题，采用何种水下目标跟踪结果是实用可靠的，如何解决点估计无法表达示向性误差的问题是重点，研究一种实用、快速、评估完善的水下纯方位目标跟踪方案具有重要的工程实践意义。

纯方位目标最优点估计算法根据马尔可夫性可分为定位跟踪算法、滤波跟踪算法等[4]。Doğançay[5]基于Stansfield估计器提出线性最小二乘法算法(Linear Least Square, LLS)，根据高斯-马尔可夫(Gause-Markov)定理，在各平台测量误差为零均值，且方差互不相关时，实现基于方差最小准则下的最优估计，但该算法忽略了各平台测量误差的差异性。加权最小二乘算法(Weighted Least Square,WLS)对LLS进行改进，引入加权矩阵对修正平台测量误差不同的影响，但该算法为有偏性估计[6]。总体最小二乘算法(Total Least Square, TLS)使用校正系数矩阵和数据向量，但存在奇异值分解困难对定位造成消极影响[7,8]。基于最小二乘法系的定位算法均存在矩阵运算，加大了计算时间复杂度对于实际战场决策起到负面影响。三角解析定位通过平台对目标的示向线交点信息进行直接求解，提高了定位计算速度，一般有重心法、内心法、斯坦纳点法[9,10]，经统计分析内心法的定位精度最高，但定位效果仍远低于LLS，设计一种改进的解析定位算法具有研究意义。

针对水下目标跟踪所面临的困难，以点迹组成的水下目标跟踪轨迹存在两个缺点，一是本身测向信号经处理后的量测方位信息经过融合处理对目标状态估计，存在累计估计误差且无法表示误差大小，没有建立直观的容错区域思想导致实用性差；二是针对最优点误差评估指标，通常为方差及均值偏离程度，或通过利用不确定区域面积表征目标跟踪精度，忽略了不确定区域自身在空间上的几何特征优势，若利用不确定区域作为目标跟踪结果对其进行评估更符合水下环境的目标跟踪。

以不确定区域的统计结果作为衡量纯方位目标定位精度的指标大致分为以下几类，圆概率误差(Circular Error Probable, CEP)，用来表征目标位置的估计值偏离估计均值的不确定性程度[11]；定位模糊面积，受纯方位量测信息的几何特殊性，将目标位置近似为一多边形并以其面积作为定位精度优劣的考量[12,13]；置信椭圆(Confidence Ellipse,CE)，即对于某个无偏量的估计精度的多维度量，该估计量以某一概率落入一椭圆区域体时该区域的面积[14,15]；特别地，CE由联合概率密度构建，最符合实际工程上对目标估计位置的AOU表示。针对联合概率分布近似已知的情况下，不难获得目标存在于该区域的置信度，AOU本质为区间估计更适合作为水下目标估计结果，具有更好的实用性。

本文提出基于AOU的水下纯方位目标跟踪方法，有效解决水下复杂环境中纯方位目标跟踪结果缺少示向性位置误差的问题，为保证完整性分别对基于滤波和定位点估计为先验知识的不确定区域构造算法进行研究，并利用置信度及AOU精确度指标，实现了对水下目标跟踪区域的精准有效评估，为实际战场态势估计提供更多信息保障，为后续决策提供重要支撑。

2 纯方位定位模型

(1) 目标运动学模型。 本文以2维空间下对目标运动过程进行仿真建模，假设k时刻的目标状态表示为X(k)=，xk和yk分别表示k时刻目标x和y轴方向上的位置信息，和分别表示k时刻目标x和y轴方向上的速度信息，针对水下目标运动特点，本文选择匀速直线(Constant-Velocity, CV)模型对目标运动状态进行建模。目标的离散时间状态方程的一般式为

其中，F为状态转移矩阵，G为系统噪声传输矩阵，w(k)为目标运动产生的加速度噪声，符合2维零均值的高斯向量，即w(k)～N(0,σ2)，Gw(k)为过程噪声，模拟被测目标运动时受水下复杂环境等不确定因素的影响。

(2) 平台量测模型。 因海洋环境噪声和小孔径平台测量能力不足带来的影响，纯方位定位模型中，平台对目标的测向结果受平台位置误差扰动和测量误差扰动，平台对目标量测方程的离散表达式为

其中，由纯方位定位性质决定，z(k)表示k时刻的方位观测值，xt,yt分别代表目标的x和y轴方向上的位置信息，xp,yp分别代表观测平台的x和y轴方向上的位置信息，方位角θk定义为平台量测示向线与y轴方向的夹角。测向误差Δεi是服从零均值高斯分布的随机变量，导致各平台示向线无法汇聚于同一点，一般地，定位算法利用多组观测信息对目标进行估计。

3 改进解析定位算法理论

对于水下纯方位目标定位问题，目前比较流行的定位算法是利用最小二乘法对目标进行求解，然而该算法存在两个不足：(1)未考虑各平台自身测量误差的差异性，对于每条示向线的权值分配平等，未考虑大误差量测导致的异常示向信息可能对目标估计造成的负面影响；(2)公式中含大量矩阵和逆矩阵运算，并不适用于某些实时性要求较高的水下目标跟踪场景。

针对上述算法的不足，本文提出一种基于变权解析定位算法，其优势在于：(1)本算法本质属于三角解析算法，故不涉及矩阵运算减小了目标定位的运算耗时；(2)通过设置对比阈值排除异常点，利用目标估计点与示向线交点距离信息对权值进行自适应配置。具体实现步骤如下：

(1) 获取示向线交点坐标。假设多平台数目为M，则各平台对目标定示向线交点坐标(xij,yij)，所有交点集合表示为

(2) 设定筛选规则。通过内心法定位[10]求解获得一次点估计解(xcp,ycp)，将一次估计点与各平台示向线交点距离disij，而后根据设定阈值γ，用于筛舍异常点或干扰项得到一次筛选交点集合Snew

(3) 设定权值调整规则。本算法考虑聚类程度较高的交点对点估计的权重较大，故设定权值调整规则应考虑近大远小的规则，将估计解与一次筛选交点集合的各距离倒数作为权值项Weightindex

(4) 整理表达形式为

本算法针对纯方位定位出现的异常点问题，加入阈值筛选步骤，并通过对于各交点进行权值动态匹配，实现对目标快速精准的位置估计。

针对水下复杂环境下的纯方位目标跟踪技术，最优点估计缺乏示向性的位置误差表示，对实际战场决策必然带来负面影响，下节将研究本文重点内容，即提出一种基于不确定区域的水下目标跟踪方案。

4 不确定区域构建算法理论

本文提出基于不确定区域(AOU)的水下目标跟踪估计方法替代最优点作为目标定位状态，为保证完整性，本节主要研究内容：(1)以扩展卡尔曼滤波为代表的非线性滤波法下更新状态协方差作为输入的AOU构建方法；(2)以最优点估计为先验知识的基于最大后验概率的AOU构建方法，如图1所示。

图1 基于最大后验概率的AOU构建流程图

4.1 基于扩展卡尔曼滤波的不确定区域构建算法

(1) 基于扩展卡尔曼滤波算法下的水下目标跟踪模型。 扩展卡尔曼滤波(Extended Kalman Filter,EKF)算法的基本思想是截取非线性函数的泰勒展开式的1阶项，忽略其余高阶项，将非线性函数近似线性化，采用卡尔曼滤波框架对目标状态进行估计。针对水下纯方位目标跟踪，其量测信息与目标状态信息具有非线性关系，对非线性函数f(·),h(·)分别对滤波值做1阶泰勒级数展开，得到线性化的状态与观测更新方程

(2) 2维联合高斯概率密度推导精确误差椭圆表达式。 考虑平台本身方位量测误差符合高斯分布下，再根据乘性高斯分布仍符合高斯分布的特点，故对目标位置不确定区域估计应为椭圆区域，结合水下纯方位目标跟踪量测信息较少，故通过大量采样信息经统计处理的不确定区域构建是不可行的，该节采用一种基于状态协方差矩阵分解的置信椭圆构建方式。

(a) 建立椭圆方程。已知目标状态的概率密度分布为高斯分布，则目标出现在该区域的概率应为

其中，p(k+1)代表被测目标在k+1时刻的真实位置，代表被测目标在k+1时刻的估计位置目标的位置协方差矩阵应表示为对式(10)求导可得置信椭圆表达式为

其中，c为置信系数，与置信椭圆的区域大小及置信度有关，具体对应关系见如式(12)的推导

则置信系数c与置信度Pe之间的关系为

(b) 置信椭圆长短轴。需对目标的位置协方差矩阵Pk+1|k进行特征值分解，这里求解过程不加赘述，求得长轴E与短轴F的表达式为

(c) 定义置信椭圆的椭圆旋转角度β。置信椭圆长轴与坐标系水平坐标轴构成的倾角

首先，科学家自律与科技协会的自治相结合。科学家是一个相对自由的职业，其遵循特定的科学规律，因其专业性使得外界无法全面介入。因而要求科学家能够自律，主动地遵守法律和伦理规范。同时，科技领域存在各种协会，这些协会的重要使命一方面是为科学家服务，另一方面也对科学家的活动进行规范和治理，当出现违法或者违背道德的会员科学家时，科技协会可以对其进行惩戒。因此，科学领域的自律，一方面是科学家要严于律己；另一方面科技协会要加强对科学家的规范和管理。

通过以上步骤可见，以目标在该时刻的状态协方差作为输入，通过特征值求解构建目标位置置信椭圆，对目标跟踪评估指标延伸为不确定区域置信度与该区域面积所表征的跟踪精度，实现跟踪评估的多维考虑。

4.2 基于最大后验概率的不确定区域构建算法

对于水下纯方位目标跟踪问题，一般基于非线性滤波算法拟合被测目标运动轨迹较为精准，但涉及观测异常或实际运动目标出现强非线性轨迹的影响会导致目标跟踪出现失效等问题，对于后续指控策略带来严重影响。根据以上潜在问题，本节研究以直接最优估计点为先验利用最大后验概率(Maximum A Posteriori, MAP)算法对目标位置不确定区域的构建方法，该方法无需协方差矩阵分解步骤，有效提高目标位置区间估计速度，在滤波跟踪不收敛情况下提供了准确的备用信息补充。具体实现流程如下。

(1) 基于MAP的定位修正算法。利用基于变权解析定位算法解，作为初始估计点Xcp(xcp,ycp)，通过基于贝叶斯后验概率的定位法进行修正，在多平台纯方位目标跟踪场景下，平台方位量测的条件概率密度函数应为

其中，θ0i为平台与目标的理想示向线，θi为估计角度，根据几何关系(见式(3))可得

其中，m(θ)为边缘概率密度与x无关，f(θ)为先验信息的概率分布，但由于无先验信息分布则设定f(θ)=1，这里再引入归一化常数ω，则后验概率应符合

若求使π(x,y|θ1,θ2,...,θn)达到最大值(x,y)，需要对该函数进行非线性优化，设优化函数为

为解决上述公式的非线性问题，可采纳线性化方法见公式同样的记指数项为Fi(x,y)

(2) 非线性化近似不确定区域模型。以平台观测噪声方差及其位置信息为先验知识下的AOU模型构造。由式(22)得后验概率密度π(x,y|θ1,θ2,...,θn)近似为2元联合正态分布密度函数π(x,y|θ1,θ2,θ3)≈N(x,y|θ1,θ2,θ3)， 即

对式(23)求导可得不确定区域估计为

同上节，置信系数k的取值与置信度有关，详细推导见式(11)-式(13)，这里不再赘述。

(3) 置信椭圆长短轴与椭圆旋转角设定。为方便后续理解，针对式(25)一般椭圆方程经旋转变换在原始坐标系的表达形式应为

其中，β为椭圆长轴与横坐标轴夹角， 即椭圆的旋转角，其确定方式分为以下两种情况讨论：

当B=0，代入式(25)易得，不确定区域为无旋转角的标准椭圆方程，故旋转角一般取0, π/2；

若B ̸=0，根据应用三角函数关系，可得tanβ=，故还需对于A和C还需要分3种情形讨论，具体符号确定原则及椭圆旋转角结论见表1。

表1 旋转角 β的符号确定原则

5 目标不确定区域跟踪仿真实验

5.1 仿真态势1

以2维平面上单目标运动的跟踪为例进行仿真分析，分别在30 s, 60 s处进行变向CV运动，设定本态势目的：(1)分析非线性滤波在跟踪强非线性运动目标时，其跟踪效果与定位跟踪效果进行对比；(2)定位跟踪在何种态势下定位效果出现失准，并在此时与滤波跟踪效果进行对比。具体仿真参数如表2所示。

表2 仿真参数

图2(a)为仿真态势1下的水下纯方位目标跟踪轨迹，其中，目标轨迹均为不确定区域构成，蓝色AOU轨迹为目标在滤波跟踪下基于EKF的AOU轨迹图，红色AOU轨迹为目标在定位跟踪下基于MAP的AOU轨迹图，黑色圆点表示目标在该时刻的真实位置，作为本文目标跟踪方案有效性的衡量标准。在60 s目标出现强非线性变向运动，可见滤波跟踪效果出现小幅偏差，并在68 s左右跟踪复位，在此时间段内定位跟踪效果较为稳定无过大偏差；在约70 s时平台间与目标近似处于平行的态势下，基于MAP的AOU在该方向上的位置误差接近10 km，结果可见基于EKF的AOU在该态势下跟踪效果较为准确。

图2 基于不确定区域的目标跟踪轨迹及其面积

图2(b)为2类跟踪下不确定区域面积表征跟踪估计的精确度，对应统计学均方根误差(2次型)指标，可见在目标跟踪初期基于EKF的AOU面积较大约达至30 km2，基于EKF的AOU面积较小，与初始协方差设定有关，在0～30 s目标跟踪的AOU面积呈减小趋势，符合平台目标距离与量测误差的关系，在60 s时滤基于EKF的AOU随目标变向导致AOU面积小幅增加，在约70 s时基于MAP的AOU面积出现跳变，其面积约为5 km2，以上结果均符合图2(a)的结论，证明该态势下两种跟踪算法的估计精度均较为理想。

图3(a)为单次仿真下2类跟踪AOU置信度表征跟踪估计的准确度，对应统计学均值偏差(1次型)指标，置信度迭代规则以AOU是否包含当前目标真实位置为准。可见2种基于AOU的目标跟踪轨迹的置信度均在95%左右，在70 s左右可见基于MAP的AOU因平台与目标相对态势变差导致置信度出现下降的情况。

图3 仿真态势1下的不确定区域置信度

图3(b)为利用蒙特卡罗方法该态势下的目标跟踪AOU的统计置信度信息，可见基于MAP的AOU置信度综合较高，且起伏在81%～97%，基于EKF的滤波跟踪AOU置信度相对较低，且起伏在84%～94%。

综合图2、图3通过对基于AOU的目标跟踪轨迹分析可知，在平台与目标接近平行的态势下，基于MAP的AOU跟踪效果差于基于EKF的AOU跟踪效果，此结论与该态势下纯方位定位弱可观测性有关；在被测目标出现强非线性运动时，基于EKF的AOU跟踪效果较差，此结论与EKF本身线性化缺陷有关。通过以上结论说明基于AOU的水下纯方位目标跟踪方案所得结论与实际跟踪理论一致，证明本跟踪方案的有效性。

5.2 仿真态势2

以2维平面上单目标运动的跟踪为例进行仿真分析，分别在30 s, 60 s处进行变向CV运动，设定本态势目的：(1)平台目标间距离越大时对目标AOU的精确与置信指标产生何种影响；(2)对于初始状态设置误差较大时目标跟踪效果；(3)通过改善目标平台间的态势，跟踪效果如何改变。具体仿真参数如表3所示。

表3 仿真参数

图4(a)为仿真态势2下的水下纯方位目标跟踪轨迹。在0处设定初始目标状态与目标真实状态偏差较大且初始协方差设置极小，跟踪结果表明，EKF跟踪算法仍可进行收敛有效跟踪，在目标位置距离平台较远且处于劣势态势下，基于MAP的AOU在该方向上的位置误差为15～20 km。

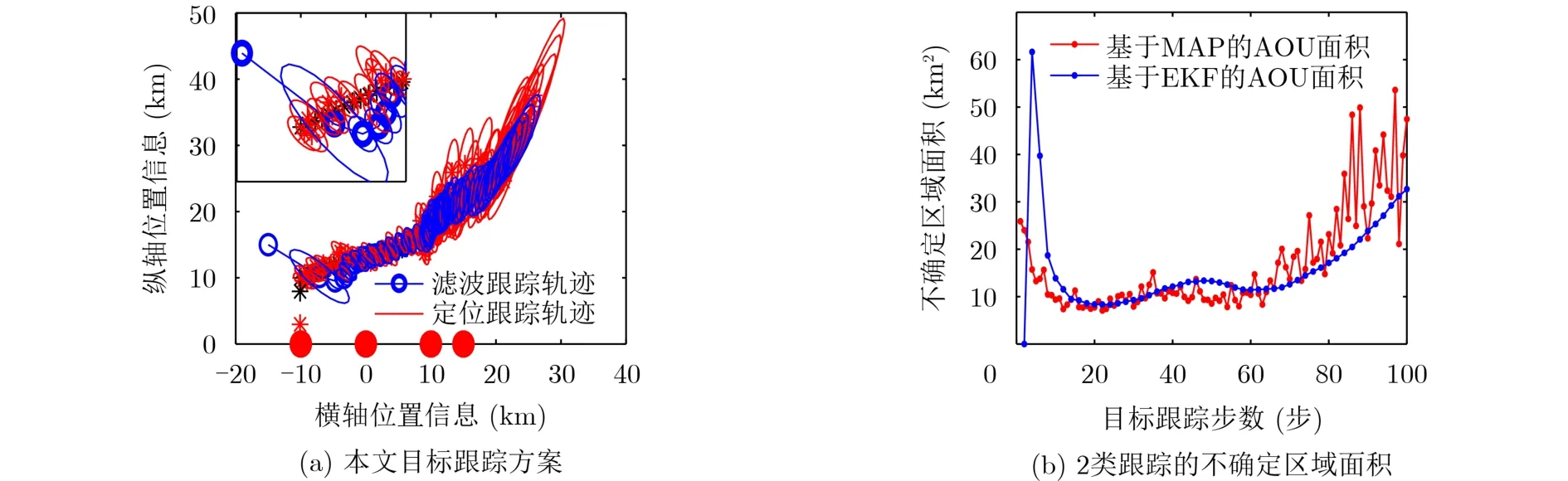
图4 基于不确定区域的目标跟踪轨迹及其面积

图4(b)为2类目标跟踪下AOU面积表征跟踪估计的精确度，可见在目标跟踪之初基于MAP的AOU面积较大约达至25 km2，基于EKF的AOU面积达至60 km2，这与初始协方差设定有关，在0～30 s目标跟踪的误差区域面积呈减小趋势，表明态势转优给目标跟踪精度带来的正面影响，在30～100 s时AOU面积增大，尤其60 s后基于EKF的AOU面积较小，表明滤波跟踪在较远距离时跟踪效果较好。

图5(a)可见2种基于AOU的目标跟踪轨迹下的置信度分别为88%和91%，证明该区域内对目标位置估计的有效性。针对态势2而言，基于MAP的AOU在跟踪初期可信度较高，基于EKF的AOU在跟踪后期可信度更高。图5(b)为利用蒙特卡罗方法该态势下的目标跟踪AOU的统计置信度，可见基于MAP的AOU置信度综合较高，起伏区间在81%～96%，基于EKF的AOU置信度相对较低，起伏区间在86%～93%，其中，出现少量置信跌底情况，考虑初始状态设定不当，运动目标变向非线性程度较强导致滤波跟踪不收敛的情况。

图5 仿真态势2下的不确定区域置信度

综合图4、图5结果分析可得，若出现明显态势优化的情况，目标AOU跟踪精度有所提升，若无明显态势改变情况下，平台目标间距离越大对目标AOU面积增大即跟踪精度下降，对于初始状态设置误差较大情况，基于EKF的AOU跟踪仍可实现跟踪收敛，但面临较大误差或强非线性运动目标跟踪会出现跟踪发散的情况。

6 结束语

针对水下目标点估计跟踪存在无示向性位置误差的问题，本文提出基于AOU的水下目标跟踪方案，同时引入区间置信度的统计概念以及表征跟踪结果精确度的AOU面积作为评估标准，为后续决策提供清晰的容错与判断区域，提高了跟踪结果的实用性。针对LLS定位存在的不足，提出了基于变权解析定位算法，为构建基于MAP的AOU提供了先验知识。仿真结果所示，针对目标平台间距离分别为10 km内和20 km内的跟踪场景：(1)对应AOU面积分别为10 km2以内和20 km2以内，表明了AOU构建的有效性及精确性；(2)对应AOU置信度水平为90%和87%左右，表明了目标AOU轨迹的可靠性及准确性。并针对不同仿真态势，得出了基于MAP与基于EKF的AOU目标跟踪方案的适用范围，对于近距离强非线性运动目标进行跟踪，基于MAP的AOU跟踪效果较好，对于远距离运动目标进行跟踪，基于EKF的AOU跟踪效果较好。综上所述，基于不确定区域的水下目标跟踪方案是有效可行的，且该跟踪方案包含明确的估计区域及其区间置信度，为实际战场态势估计提供更多信息保障，为后续决策提供重要支撑。