IRS增强信息与能量同传赋能物联网的鲁棒公平性资源分配算法

李世党 陈 锦 陈影影 龙春梅 徐劲松 李春国

①(江苏师范大学物理与电子工程学院 徐州 221116)

②(江苏师范大学地理测绘与城乡规划学院 徐州 221116)

③(江苏师范大学中俄学院 徐州 221116)

④(东南大学移动通信国家重点实验室 南京 210096)

1 引言

第5代通信(Five Generation Communication,5G)通过利用不同的先进技术，极大地提升了频谱效率和能源效率性能[1-3]。然而，这些技术普遍要求较高的功耗和实现成本，构成了设计实用移动通信系统的障碍。例如，物联网设备受到电池容量的限制，这成为物联网生存周期延续的瓶颈[4,5]。因此，需要一个可扩展和可持续的解决方案来实现无处不在的连接和为6G驱动的物联网中的巨量设备提供持续的能源供应。近年来，智能反射面(Intelligent Reconfigurable Surface, IRS)作为一种具有较高波束形成增益、显著降低能量消耗和硬件成本的新技术成为解决上述瓶颈的极具潜力的备选方案，引起工业界和学术界的广泛关注[6-9]。IRS可以安装在建筑物的外部，通过减少基站的传输功率支持更加绿色的通信需求。特别是，IRS是由安装在平面阵列上的大量可调无源单元组成的，这些单元巧妙地协调起来反射信号，以建立更有利的无线传播通道，实现更可靠的通信。这些无源元件具有较高的成本效益和能源效率，同时又可以智能地调整相位，独立地引导入射信号。因此，反射信号可以在所需的接收端进行相干组合，进而提高接收端的信干噪比。因此，IRS作为一项颠覆性的技术，可以智能化调配无线通信环境，使得可以让当前的“哑”环境变得更加智能化，这可能会在下一代移动通信中惠及交通[10-12]、医疗[13]、智慧城市[14,15]等广泛的垂直行业。

为了解决5G驱动的物联网通信场景中巨量传感节点的可持续供电的问题，信息与能量同传(Simultaneous Wireless Information and Power Transfer, SWIPT)技术应运而生[16-19]。具体来说，该技术允许每个用户根据接收到的信号同时进行信息解码和能量收集。考虑到各种接收器的灵敏度，在信息与能量同传系统中有两种典型的接收器架构，分别是功率划分和时间划分[16]。对于PS体系结构，单个用户可以使用功率划分器将接收到的信号按指定的比例分成两个不同的功率流，其中一个流用于信息解码，另一个用于能量采集[17]。文献[18]研究了同时存在有信息用户和能量用户的多用户MISO网络，通过优化信息波束和能量以最大化总收获功率的加权总和。进一步，文献[19]研究了功率划分架构下的功率最小化的问题，提出了一种最优化的算法和低复杂度的次优算法，研究结果表明相比于时分架构，功率划分架构可以更好地节省系统的功率损耗。值得注意的是，在信息与能量同传通信系统中，路径损耗是影响用户侧能量采集高低的重要因素。幸运的是，在基于功率划分的信息与能量同传通信网络中，通过联合IRS和多天线技术，利用基站侧和IRS的双重波束形成增益，可以有效地提高能量采集的效率。

在IRS和信息与能量同传融合方面，已有较多的研究成果[20-24]。例如，文献[20]研究了IRS辅助的SWIPT网络中的加权和功率优化问题，以期延长IRS辅助的信息与能量同传网络中的无线覆盖和设备的电池寿命。特别地，它推广了文献[18]中的结果，仿真结构表明对于任意通道的用户，不需要专门的能量波束，从而有助于降低实现复杂度。文献[21]研究了IRS辅助的信息与能量同传MISO下行通信网络中最小化总传输功率的问题，提出了一种基于惩罚的算法，由于该算法可以分布式实现，从而为未来的技术落地提供了可能。进一步，文献[22]研究了分离式能量用户的场景下公平性能量采集最大化问题，为了求解该问题，利用交替算法和半正定松弛技术获得原始问题的次优解。此外，文献[23]考虑了IRS辅助网络中的多输入多输出场景，在最大化所有信息用户的加权和速率的目标下，提出了一种较低复杂度的迭代算法，以平衡最优性能和计算复杂度。文献[24]针对IRS辅助的信息与能量同传通信系统中的能量效率最大化问题，通过联合优化基站侧和IRS的主被动波束成形矢量及功率划分因子，实现数据速率和功率损耗之间的权衡。然而，由于IRS缺乏射频链路，所以IRS无法精确地估计IRS到移动用户的信道信息。因此，以上研究工作不能直接推广到IRS辅助功率划分架构下的多用户信息与能量同传系统中。

为了解决不完美信道状态信息下系统无法精确调配资源的问题，本文针对IRS辅助的MISO-SWIPT系统，提出了一种新颖的基于采集能量公平性最大化的鲁棒资源分配方案，从而确保网络中采集能量的公平性，同时满足所有用户的信干噪比约束和相位的模一约束。由于信道不确定性的影响，使得无法直接求解。为了获得该问题的解，本文首先采用Schur-Complement将非线性不等式约束转化为线性矩阵不等式约束，进而利用S-Procedure去除信道不确定对原始问题的影响，最后提出了一种新颖的交替迭代优化鲁棒算法。仿真结果表明，所提鲁棒资源分配算法可以获得良好的公平性采集能量性能，且可以充分利用智能反射面带来的额外的自由度提升系统资源调配的有效性。

2 系统模型

考虑一个IRS辅助的SWIPT网络模型，该模型中包含一个配置有M根天线的基站、N个反射单元的IRS和K个单天线的用户。为了延长网络生存周期，每个用户采用功率分割技术，使得每个用户可以同时进行信息解码和能量采集。定义用户集合为K={1,2,...,K}(∀k ∈K)，IRS的阵列单元集合为N={1,2,...,N}(∀n ∈N)。令H ∈CN×M表示从基站到IRS的信道，hb,k ∈CM×1表示从基站到第k个用户的信道，hr,k ∈CN×1表示从IRS到第k个用户的信道。令Θ=diag(q)表示IRS的相控矩阵，其中q=，θn ∈[0,2π)。则基站侧的发送信号可表示为

其中，sk为发送给第k个用户的信息且满足wk为相应的发送波束矢量，ve表示专用的能量波束且满足ve～CN(0,Ve)。因此，第k个用户接收到的信号可以描述为

其中，ρk ∈[0,1]表示用户k的功率分割参数，nk～CN为用户k进行功率分割操作引入的噪声。

依据式(3)，用户k的信干噪比可表示为

其中，假设所有的用户已知专用的能量波束ve，则所有的用户在解码期望信息之前将能量波束产生的干扰消除。与此同时，用户k接收到的进行能量采集的信号为

本文的能量模型采用文献[20]中的线性模型，则用户k采集到的能量为

其中，ηk ∈[0,1]为用户k的能量转换参数。相比于用户收到的信号功率，用户处的噪声功率是非常小的，因此，式(6)中的噪声功率可以忽略不记。

由于IRS缺少射频链路和信号处理单元，所以无法精确估计从IRS到用户的信道信息，导致从IRS到用户的信道存在误差。本文考虑式(7)的欧几里得误差模型

3 鲁棒资源分配方案设计

本小节通过优化功率分割因子、主动波束成形矢量和IRS处的被动相位矩阵，以期实现在基站的最大功率约束、用户处的信干噪比约束和相移模1约束下所有用户中最小的采集能量最大化。

3.1 问题建模

考虑的公平性能量采集最大化优化问题可以描述为

其中，C1为基站的最大功率限制约束，C2为用户k的信干噪比约束，γmin为用户所需的最小信干噪比阈值，C3为功率分割因子的约束，C4为相移矩阵的模1约束。由于信道的不确定、变量耦合以及非凸的模1约束C4，优化问题式(8)为非凸问题，难以直接得到该问题的解。为了使得优化问题式(8)便于求解，首先利用Schur引理和扩展S引理将无限维约束等价转换为有限维约束的问题，然后利用块坐标下降法进行交替求解。

3.2 优化问题式(8)等价转换(1)

引入松弛参数t，则优化问题式(8)可以重新表述为

引理1[25](S c h u r C o m p l e m e n t)：假设X ∈Sn的分块矩阵为

其中，A ∈Sm，则关于矩阵A，X的Schur补为D=C-BTA-1B。式(11)成立的条件是当且仅当A ≻0且D≽0。

将hr,k=+Δhr,k代入式(10)，利用引理1，可以进一步得到

其中，

其中，G=ΘH。然而，因为信道hr,k的不确定性，使得式(12)仍然为无限维约束，为了进一步转换为便于处理的线性矩阵不等式约束，需要利用文献[7]中的引理。

引理2[7]如果存在半正定矩阵Di≽0,i ∈{1,2}，则一定存在ti ≥0，使得如下矩阵不等式约束

等价于线性矩阵不等式(14)

其中，

基于上述数学操作和分析，原始优化问题可以等价转换为

虽然问题式(20)的约束都是凸约束，但优化参数之间的相互耦合致使该问题仍为难以求解的非凸问题。幸运的是，借助交替优化技术可以对优化参量进行解耦。

3.3 优化问题式(8)等价转换(2)

为了解耦优化参数，需要采取交替迭代优化技术，即固定相移矩阵Θ，求解Wk,ρk,πk,χk,t,Ve；固定Wk,ρk,πk,χk,t,Ve，求解相移矩阵Θ。

子问题1：优化Wk,ρk,πk,χk,t,Ve

当相移矩阵Θ固定，则关于优化参数Wk,ρk,πk,χk,t,Ve的问题为

由于非凸约束C9和非凹代价函数t2，问题(21)仍是关于参数Wk,ρk,πk,χk,t,Ve的非凸问题。首先，采用半正定松弛方法，将C9约束丢弃；然后，利用泰勒级数展开方法，则

此时，优化问题式(21)可重构为

此时，问题式(23)是关于Wk,ρk,πk,χk,t,Ve的凸问题，因而可以运用连续凸逼近方法进行求解，利用CVX数值工具就可以得到,t*,。然而，通过上述过程求解得到的不一定能够满足rank()=1。此时，如果求解的满足rank()=1，则利用奇异值分解得到最优的发送波束成形矢量；否则，需要利用高斯随机化的方法重构满足rank()=1的解。

子问题2：优化Θ

其中，

式(25)中的非凸约束部分1≤|qn|2可以被线性化为

经过上述数学操作后，则问题式(27)可以转换为

显而易见，转换后的问题(32)是凸问题，因此可以借助凸优化的数值工具CVX进行求解。通过子问题1和子问题2的迭代解决了原始问题(8)，相应的算法流程如算法1所示。

4 仿真分析

为了评估所提鲁棒算法的有效性，本文将所提鲁棒算法与等功率分割因子的鲁棒算法(ρk=0.5)，完美信道信息下公平性能量采集算法以及传统的无IRS辅助的鲁棒算法进行对比，将完美信道信息下公平性能量采集算法、传统的无IRS辅助的鲁棒算法和等功率分割因子的鲁棒算法分别标记为比较算法1、比较算法2和比较算法3。假设基站的位置为(3.5 m,0)，IRS的位置为(0,6 m)，所有的单天线用户随机分布在以(3.5 m,6 m)为圆心，半径为2 m的区域内。本文采用的路径损耗模型为L(d)=，其中C0=为参考距离D0=1 m时的路损，d为节点之间的距离，α为路径损耗指数。假设基站到IRS和用户的路径损耗指数分别为αBI=2.2和αBU=3.6，IRS到用户的路径损耗指数为αIU=2.4。假设基站到所有用户的信道服从瑞利衰落，与IRS相关联的两个信道H和hr,k服从莱斯衰落，其中莱斯因子设置为10 dB。下文如无特别说明，相应的仿真参数设置为用户数K=4,Nt=8,Lmax=100，相移矩阵的维数M=30，噪声功率为基站的最大发射功率值为30 dBm，每个用户所需的最小信干噪比为10 dB。假设所有的信道误差半径相同，定义信道误差界为εk=ϵ‖Δhr,k‖F，其中ϵ ∈[0,1]描述信道的不确定性程度，本文将ϵ设置为0.05。

图1展示了所提鲁棒算法在不同信道误差半径ϵ下公平性采集能量的收敛曲线。从图1中可以观察出，所提算法经过2～3次就可以很快地达到稳定值，因此所提鲁棒算法具有良好的收敛性能。与此同时，随着信半径ϵ的增大，所提的鲁棒算法能够采集到更少的能量。因为随着信道误差半径ϵ的增大，为了对抗信道不确定性对公平性采集能量性能的影响，需要分配更多的发射功率，从而导致网络中的可用资源的自由度减少。

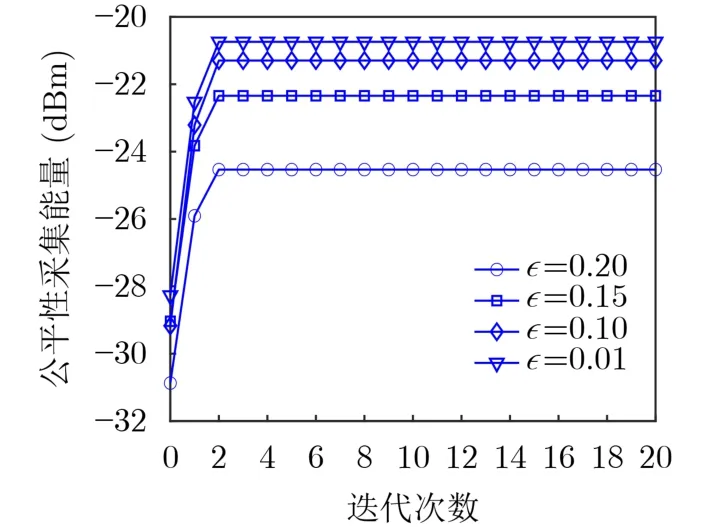
图1 所提鲁棒算法的收敛性能

算法1 所提鲁棒优化算法

图2展示了几种传输方案的公平性采集能量性能随着基站的最大允许发射功率的变换对比。从图2中可以观察出，随着基站最大允许发射功率的增大，所有算法的公平性采集能量也相应增大。此外，相比于比较算法2，所提鲁棒算法可以获得较好的公平性采集能量性能，从侧面也说明：增加了IRS后，可以有效地配置资源，使得用户获得更多的能量。由于所提鲁棒算法优化了功率分割因子，所以相较于比较算法3，所提算法获得了更好的公平性采集能量性能。然而，由于信道不确定性的影响，相比于比较算法1，所提鲁棒算法的公平性采集能量性能有所下降。

图2 不同的发射功率对公平性采集能量性能的影响

图3展示了几种不同算法的公平性采集能量性能在不同的用户所需最小的信干噪比γmin的变化曲线。由图3可以看到，随着用户所需的最小信干噪比γmin的增加，几种算法的公平性采集能量性能相应降低。主要原因是为了满足更苛刻的约束C2，基站需要分配更多的功率进行自身信息解码，进而导致分配给每个用户进行采集能量的功率减少，使得所有用户中最小的采集能量降低。此外，还可以看到，即使信道存在有误差，由于所提算法可以充分利用部署IRS带来的额外阵列自由度进一步提升采集的能量，所以所提的鲁棒算法的公平性采集能量性能仍然高于比较算法2。然而因为信道的不确定性，网络无法准确配置资源，因此所提鲁棒算法的公平性采集能量略低于比较算法1下的公平性采集能量性能。

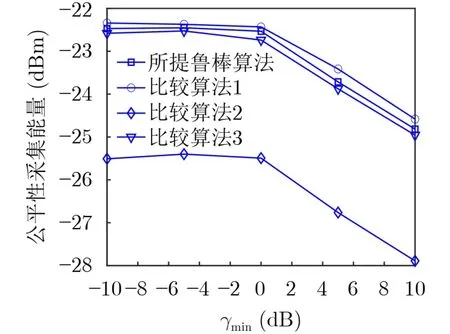
图3 不同的γmin对公平性采集能量性能的影响

为了评估不同发射单元数目对于性能的影响，图4展示了不同反射单元数目下对公平性采集能量性能的影响。根据图4可以观察出，比较算法2的公平性采集能量与反射单元数目没有关系，主要是因为已经去除了IRS的反射单元，增加反射单元数目对于公平性采集能量性能不会产生任何影响。随着反射单元数目的增加，所提算法、比较算法1、比较算法3等3种算法的公平性采集能量性能增大。这一发现进一步验证了配置越多数目的反射单元，系统中相应的反射路径也相应增多，网络中用户的公平性采集能量也就更多。

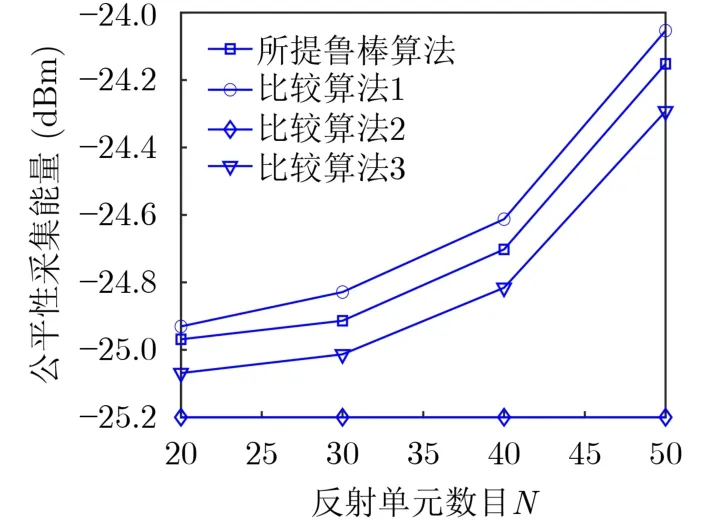
图4 不同反射单元数目对公平性采集能量的影响

5 结论

本文对智能反射面辅助的多用户SWIPT网络中基于公平性采集能量的鲁棒资源优化设计开展了研究。假设IRS与用户之间的信道存在误差，在发射机总功率约束、用户信干噪比受限和反射幅度模1约束下，建立了用户公平性采集能量最大化问题。利用Schur-Complement和S-Procedure将无限维约束转换为有限维的矩阵线性不等式，然后利用罚函数和连续凸逼近的方法将难以求解的原问题转化为标准的凸优化问题。数值结果验证了所提鲁棒算法具有较快的收敛速度，并且相比于传统的鲁棒算法，所提算法具有良好的鲁棒性和公平性能量采集性能。