基于DBN网络的滚动轴承故障诊断*

刘 鹏,皮 骏,胡 超

(1.江苏航空职业技术学院航空工程学院,镇江 212134;2.中国民航大学交通科学与工程学院,天津 300300)

0 引言

滚动轴承作为旋转机械设备的重要元件,一旦发生故障将会严重影响旋转机械的正常运转,与机械设备的安全性与可靠性息息相关[1]。同时,旋转机械设备随着时代的发展变得智能化与复杂化,也随之带来振动信号数据量的激增与数据耦合较为严重等问题。此外,由于采集系统或外界干扰,轴承振动信号不可避免掺杂一些噪声,这给滚动轴承故障诊断带来较大挑战[2]。面对如此挑战,国内外专家与学者将振动信号处理方法与人工智能相结合应用于滚动轴承故障诊断,郭媛等[3]将BP神经网络运用于液压缸故障诊断中,虽取得较为不错的诊断效果,但仿真数据与机械实际运转数据存在一定差距,对实际工程应用有一定影响,且BP网络难以对复杂巨量特征进行有效提取。皮骏等[4]采用ELM网络对航空轴承进行故障诊断,并将ELM网络的诊断性能与BP、SVM、RBF等网络进行对比,虽取得不错的诊断效果,但对高维复杂数据特征提取存在困难,易陷入局部最优。通过文献调研发现,浅层神经网络面临维度灾难及分类精度低等问题,难以映射出振动信号与滚动轴承故障之间的复杂对应关系[5-6]。

为了准确且快速地对轴承故障类型进行识别分类,必须掌握先进的振动信号降噪处理技术与建立优异轴承故障诊断模型。深度学习作为人工智能领域的一个重大突破,因其强大的特征提取能力,前向无监督的训练、反向全局微调体现自身优势[7]。近些年,深度置信网络(DBN)成为深度学习领域一个经典成熟网络模型,在故障诊断领域取得了良好的效果[8-9]。DBN网络具有强大的非线性处理能力,在处理高维复杂数据方面不会陷入维度灾难,同时通过前向无监督训练学习及反向有监督全局微调两个过程,实现对故障特征的充分提取与挖掘。但DBN网络存在结构参数设置困难,完全靠经验对网络参数进行设置,严重限制了DBN网络的发展,影响DBN网络诊断的准确率。本文通过探究分析隐含层层数、数据类型、激活函数对DBN诊断准确率的影响,确定了DBN的参数,为DBN参数设置提供一种新的方法与思路。对DBN网络每个RBM单元重构能力进行验证分析,并与浅层神经网络的诊断性能进行了对比分析,进而验证了DBN网络在滚动轴承故障诊断中的有效性。

1 深度置信网络

DBN网络[10]被应用于图像识别、语音识别、故障诊断等多个领域。DBN是由多层RBM单元堆叠而成,无监督贪婪算法逐一对每层的RBM单元进行无监督训练,BP算法对全局进行微调,并由顶层Softmax分类器进行分类的深度神经网络。每个RBM通过CD-K算法进行学习训练,多个RBM堆叠,从数据中挖掘更深层次的故障特征,然后经过BP算法反向微调各层的权重与偏置,从而达到网络的最优,可以有效提高DBN的诊断准确率。

RBM是一个二分图结构的概率无向图模型,同时也是基于能量生成的模型,如图2所示。

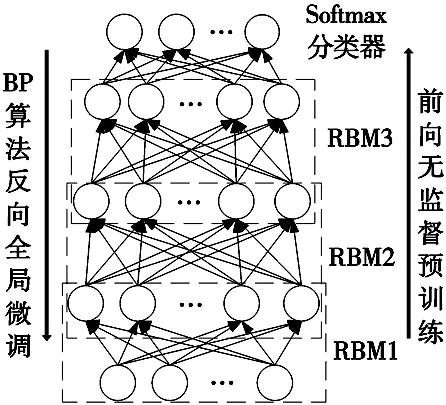
图1 深度置信网络基本结构

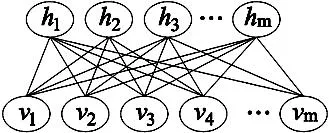
图2 受限玻尔兹曼机

一个受限玻尔兹曼机是由m个可观测变量和n个隐含变量组成,给出可观测层单元v={v1,v2,v3,…,vm}∈{0,1},隐藏层单元h={h1,h2,h3,…,hn}∈{0,1}。权重w、可观测层单元的偏置b与隐藏层单元的偏置c随机生成时,受限玻尔兹曼机的能量函数定义为:

(1)

由能量函数将受限玻尔兹曼机的联合概率分布p(v,h|θ)定义为:

(2)

Z(θ)=∑v,hexp(-E(v,h))

(3)

式中:θ={bi,cj,wij}是网络的参数,m表示可观测层节点的个数,n表示隐藏层节点的个数,wij表示可观测层节点与隐藏层节点之间的连接权重,bi表示可观测层节点的偏置,cj表示隐藏层节点的偏置,Z为归一化因子,也称为配分函数;Z(θ)为一个用来模拟物理系统热平衡的标准化常数,具有归一化的功能。

由式(2)RBM的联合概率分布函数可推出的边缘概率分布函数为:

(4)

(5)

隐藏层与可观测层节点被激活(即状态为1)的概率分别为:

(6)

(7)

由于RBM层内节点之间没有任何连接,同一层神经元之间互不相关,因而,如果知道其中一层神经元的具体值时,则另一层神经元的分布值相互独立,即:

(8)

(9)

2 轴承故障数据采集

考虑到滚动轴承真实运转环境下振动信号难以采集获取,通过对轴承故障实验进行设计,获取振动信号。以实验室采集的307型滚动轴承故障信号为例,轴承故障诊断实验装置与示意图如图3和图4所示。将实验中的转子转速设置为988 r/min,每次实验采集16个周期,每一个周期内传感器采样1024个点。307型滚动轴承几何参数如表1所示,故障类型如表2所示。轴承的划痕利用机械冲击而成,与硬物划伤相同。

图3 滚动轴承实验装置

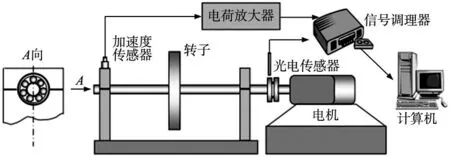
图4 实验装置示意图

表1 滚动轴承几何参数

表2 滚动轴承故障类型

不同状态的振动信号会有所不同,而时域与频域特征参数能较好的将振动信号进行映射。通过提取能反映轴承状态的参数,作为模型的输入,进而对轴承故障进行分类,是轴承故障诊断常用且有效的方法。

其中,时域与频域特征具有计算方式简单、对轴承运行状态敏感、物理意义明确等特点。因此,本文选取均值、均方根、标准差、峭度、偏度、绝对均值、波峰因子、脉冲因子、波形因子、变异系数、峰峰值11个时域特征参数与均值频率、均方根频率、绝对最大频率、绝对均值频率4个频域特征参数进行滚动轴承的故障诊断。为了更好地验证DBN模型能够处理高维非线性数据和有效提取故障特征的特点,每种故障类型选取600组数据用于故障诊断。

3 DBN故障诊断模型的建立

为了验证DBN隐含层层数、激活函数、训练集与测试集样本类型对其诊断结果的影响,从而对DBN模型予以确定,以建立完整模型。同时,为了证明DBN的优越性,对其RBM单元重构能力进行验证分析。

3.1 隐含层层数对DBN模型影响分析

DBN作为深度学习的一种成熟经典网络,与浅层神经网络最大的不同在于隐含层层数。也正是因为DBN层数的增加,增强了DBN故障特征提取的能力。由文献[11]可知,DBN的故障特征提取能力并不与隐含层的层数成正相关,选取合适的隐含层层数对诊断模型来说至关重要。寻找适合的隐含层层数,不仅能够提高DBN模型的泛化性能,还能够进一步提高诊断精度。

为了避免随意选取隐含层层数所带来模型诊断精度低、泛化能力弱等问题,本节探究隐含层的层数对诊断准确率的影响。建立隐含层分别为2层、3层、4层、5层等4种DBN模型来进行探究。当对不同网络模型进行测试时,需对隐含层节点数量进行设置。根据经验,一般高层隐含层节点数大于低层时有利于信号的压缩与故障特征的提取[12]。本文设置的4种DBN模型如表3所示。轴承正常状态、外环划痕、内环划痕、滚动体点蚀、滚动体划痕各取600组数据,5种工况共有3000组数据。其中,训练集样本数为2250组,训练集样本750组,4种模型使用相同的训练集与测试集样本,DBN模型激活函数选用Relu函数。

表3 隐含层数及节点数分布情况

从图5可以看出,4种不同隐含层层数的DBN网络的诊断准确率均随着迭代次数的增大而增加。除拥有5层隐含层的DBN模型外,其他3种DBN模型的诊断准确率都能达到收敛的状态,且诊断准确率具有稳定性。其中,具有5层隐含层的DBN网络出现大幅波动,不但准确率稳定性较差,而且其诊断的准确率较低。造成其现象的原因是具有5层隐含层的DBN由于隐含层层数过多,造成误差逐层传递,误差逐层积累,导致了模型诊断准确率的降低,故隐含层的层数不宜设置太大。此外,拥有3层隐含层的DBN网络诊断精度优于其他模型,不仅体现在诊断精度方面,还表现在模型的诊断效率。具有3层隐含层的DBN网络能够取得如此优异的诊断效果,主要得益于3层隐含层就能对轴承故障特征进行充分且适宜的提取挖掘,所选择的各层隐含层节点数量适应其模型的学习与训练。因此,DBN隐含层选取3层时,较其他模型具有较高诊断精度与诊断效率。

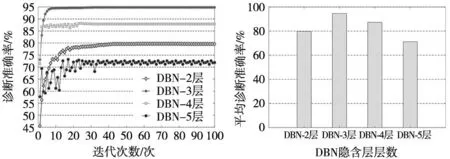
图5 不同隐含层准确率随迭代次数 图6 不同隐含层DBN模型平均诊断准确率

考虑到DBN模型每一次诊断时其诊断结果的波动性,且诊断结果具有不可复现性。为了提高DBN诊断的结果可靠性与可信服性,需对不同隐含层诊断模型进行10次重复诊断试验,并计算10次诊断结果的平均值。从图6可以看出,拥有3层隐含层的DBN诊断模型准确率可达94.68%,与其他模型相比,诊断精度最优。

3.2 激活函数对DBN模型影响分析

根据不同隐含层DBN模型诊断准确率随迭代次数变化的情况,当隐含层设置为3层时,与数据输入层、分类输出层组成5层结构的模型时,诊断准确率最高。因而,设置网络隐含层为3层,后续分析研究均采用3层隐含层。由于激活函数不仅能够有效缓解梯度消失的问题,还能加快梯度下降的速度,有效提高网络的计算效率与诊断精度,因此,有必要探究激活函数对模型的影响。

从图7可以看出,从诊断结果的整体趋势来看,分别采用不同激活函数模型诊断准确率均随迭代次数的增大而增大,但激活函数为Tanh函数时,模型诊断精度出现波动,且需要较大迭代次数才能趋于稳定状态。另外,从诊断精度来看,其精度也最低,因此Tanh模型表现不佳。此外,采用Sigmoid函数的模型在诊断精度方面确实比Tanh要出色,但其模型的收敛速度较慢,Sigmoid函数性能一般。而选用Relu函数的模型,在诊断精度及稳定性方面都表现出优异性能,明显优于其他模型,其诊断精度接近95%,其优异性能主要得益于Relu函数结构简单,能够有效缓解梯度消失的问题,且能加快梯度下降的速度。因此,当DBN模型选用Relu函数时,诊断性能最佳。

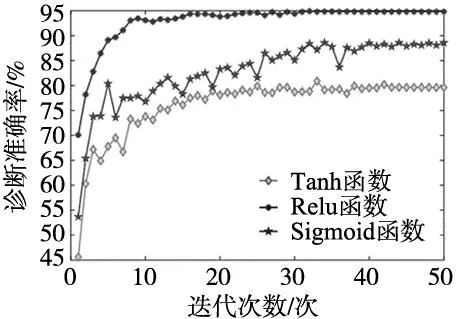
图7 诊断准确率随迭代次数变化情况

3.3 DBN网络RBM单元重构能力验证分析

RBM作为DBN网络的最小单元,其重构能力的强弱严重影响网络的特征提取能力,进而影响故障诊断精度。首先,第1层RBM单元的可观测层接收外界输入的轴承数据,通过吉布斯采样,完成第1个RBM的隐含层变量的取值。然后,隐含层变量再重构可观测层变量。如果输入原始观测层变量与重构变量之间的误差能够最小,则表明RBM单元的重构能力越强。同理,如果第2层RBM单元与第3层RBM单元的重构误差均能达到最小,则DBN模型的特征提取能力也就越强大。定义输入数据样本为X={x1,x2,x3,…,xi…,xm},重构数据样本Y={y1,y2,y3,…,yi…,ym},其中均方根误差为:

(10)

从图8可观察到,DBN模型第1层RBM的重构误差随迭代次数的增加而不断降低。虽在迭代过程中有所波动,但重构误差在迭代50次左右时,达到误差最小值为0.014 9。第2层RBM的重构误差随迭代次数的增加而不断降低,但迭代过程中其波动幅度与第1层相比波动较小,且能收敛到最低值。另外,其迭代误差收敛次数有所减小,在迭代30次左右时,就能收敛到误差值0.011 3。第3层RBM的重构误差随迭代次数的增加,先是快速下降,而后下降速度有所减慢。但在整个重构误差迭代过程中误差收敛较为平稳,未出现较大波动,呈现较好的误差收敛趋势,误差迭代次数接近20次时就已达到误差最小值0.007 1。

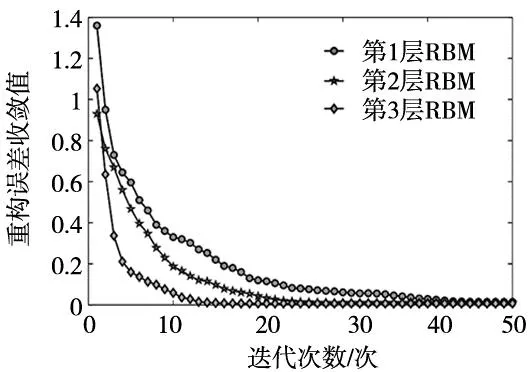
图8 3层RBM重构误差随迭代次数变化情况

值得注意的是,从重构误差收敛情况来看,DBN的3层RBM重构误差均能收敛到最低值。此外,模型训练学习过程中,随着RBM层数的增加,重构误差收敛值就越小,未出现误差逐层积累的现象,表明经对比散度优化的吉布斯算法采样效果较好。DBN模型能够对故障特征进行充分提取与挖掘,为有效进行滚动轴承故障诊断奠定了良好基础。综合以上分析可知,3层RBM单元重构误差均能达到较低值,DBN模型的每层RBM的重构能力较为强劲。

4 轴承故障诊断结果及分析

4.1 DBN与浅层神经网络对比分析研究

DBN具有特征提取能力强、处理高维数据快、收敛性能高等特点。为了验证其在轴承故障诊断中的优越性,将其与反向传播网络(BP)、概率神经网络(PNN)、极限学习机(ELM)等浅层神经网络在数据样本、诊断能力、诊断稳定性几个方面进行对比分析。

4.1.1 浅层神经网络参数设置情况说明

由于轴承共有5种工况,选取15个特征参量作为输入,因此设置BP网络、PNN网络、ELM网络的输入层节点均为15个,隐含层节点均为30个,输出层节点均为5个。另外,BP网络、PNN网络、ELM网络其他参数及激活函数均采用默认的最优状态。

4.1.2 不同数据样本诊断精度对比分析研究

从以上隐含层层数、激活函数对DBN模型的影响分析中,3层隐含层与Relu激活函数表现优异,取得了较高的诊断准确率。因此在下面数据类型对诊断模型的影响分析中,选取隐含层为3层、激活函数选用Relu函数进行以下的探究分析,其他参数的选取依然与上节相同。

实验室采集滚动轴承5种工况的振动信号,每种选取600组故障特征参数,共3000组。将样本总量按训练集与测试集分为A型、B型、C型、D型4种数据样本类型,样本类型分配如表4所示。

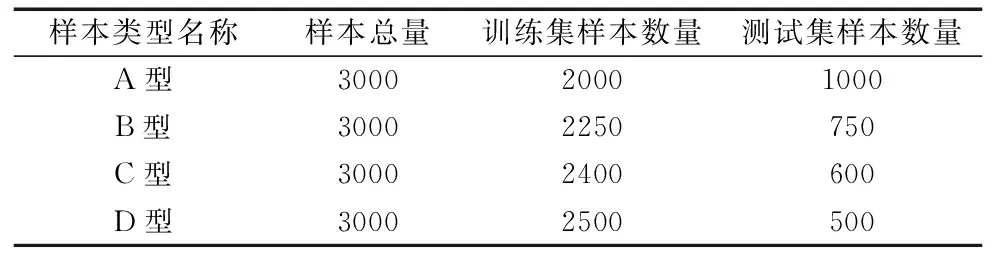
表4 4种数据样本类型 (组)

考虑到模型在进行轴承故障诊断时,诊断结果具有波动性,为了提高网络诊断的可信性,各种网络模型进行10次测试,并取其诊断结果的平均值。从图9发现,BP、PNN、ELM等网络随着训练集的增多,网络的诊断准确率呈现先增大后减小的趋势,其中BP表现最为明显。而ELM与PNN诊断准确率虽有先增大后减小的趋势,但不太明显。这表明样本集的数量对ELM诊断准确率影响不大,但可以看出较大数据样本时,浅层神经网络的诊断准确率不高,最高准确率也只达到了73.86%。

图9 不同数据样本类型测试集诊断准确率

分析其原因是,当数据样本较大时,浅层神经网络容易陷入维度灾难,或网络本身性能差,从而造成过拟合的情况。然而,DBN不仅诊断准确率最高,且对不同训练集样本来说,其诊断准确率的变化较小,4种数据样本类型下测试集样本准确率均能达到95%左右。因此,DBN在进行不同数据样本的故障诊断时其诊断能力较强,表现出故障诊断平稳性。与其他浅层神经网络相比,更适宜于滚动轴承的故障诊断。

4.2 网络诊断性能对比分析研究

通过对比DBN网络与BP、PNN、ELM在不同数据样本类型时的诊断准确率,验证了DBN网络能够适应于不同数据样本类型,同时表现出优异的诊断准确率和平稳性。为了进一步探究DBN网络与浅层神经网络在不同迭代次数时,诊断准确率变化趋势与诊断能力,对网络的诊断能力进行对比分析,进而验证DBN网络故障诊断的优越性。

从图10可以看出,随着网络迭代次数的增加,DBN网络与BP、PNN、ELM等浅层神经网络故障诊断准确率具有逐渐上升的趋势。其中,PNN网络随迭代次数的增大诊断准确率出现较大波动,分析其原因是在于概率神经网络受制于平滑因子。平滑因子的大小直接影响着PNN网络的诊断精度与诊断的稳定性,而散布常数的设置一般依靠经验进行手动或随机设置,因此造成PNN网络诊断具有不确定性与较大波动性。另外,ELM网诊断准确率与PNN相比虽存在波动,但其波动较小。值得注意的是,通过将ELM与PNN、BP等网络进行对比发现,ELM网络诊断准确率可达74.26%,其在滚动轴承故障诊断方面诊断能力略胜一筹。值得一提的是,DBN网络随迭代次数的增加,其故障诊断准确率逐步上升且较为平稳,诊断准确率达到94.83%。与浅层神经网络最高诊断准确率相比,诊断准确率高出20.57%,DBN网络的诊断准确率远高于浅层神经网络,表现出较好的诊断性能。

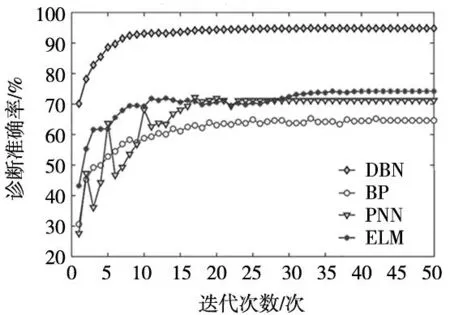
图10 不同迭代次数网络诊断准确率变化趋势

4.3 网络稳定性与诊断时间对比分析研究

考虑到在工程应用中,如果所构建的诊断模型诊断准确率存在较大的波动性,对实际诊断工作来说可行性较差,因而网络的稳定性对轴承故障诊断来说至关重要。通过将DBN网络与浅层神经网络在诊断准确率的稳定性进行对比分析,能够进一步了解DBN的稳定性,几种网络均采用训练集2250组,测试集750组数据样本进行试验,计算每种网络10次试验的诊断准确率绘制如图11所示。

图11 不同试验次数网络模型诊断准确率

从图11可以看出,不同网络模型的诊断准确率均存在波动。其中,BP模型的诊断稳定性最差。分析其原因是,BP网络易陷入局部极小,未能建立复杂映射关系,诊断平均准确率只能达到52.73%。PNN网络诊断准确率虽有所提高,诊断准确率波动及训练时间有所减小,但诊断准确率仍然不够理想。ELM网络具有较强的非线性处理能力,学习速度快,泛化性能好,有效避免BP网络的缺陷,诊断准确率有较大提升,诊断平均准确率达到71.85,稳定性也有一定的改善,但网络参数的选取较为困难,需要经过多次调试,具有很大不确定性,不太适用于实际工程问题。DBN网络与浅层神经网络相比,在滚动轴承故障诊断方面具有绝对的优势,在10次的试验中平均准确率达92.97%,且模型的诊断稳定性好,得益于DBN网络具有强大的非线性处理能力,在处理高维复杂数据方面不易陷入维度灾难,同时通过前向无监督训练学习及反向监督全局微调两个过程,实现对故障特征的充分提取与挖掘,故而能够取得较高的诊断准确率。

5 结论

(1)DBN网络RBM单元重构能力强劲。DBN第1层RBM在迭代50次时,误差值为0.014 9;第2层迭代30次时,误差值为0.011 3;第3层迭代20次时,误差值为0.007 1。随RBM层数的增加,误差收敛值就越小,未出现误差逐层积累的现象。

(2)将DBN网络与BP、PNN、ELM等浅层神经网络的故障诊断性能进行了对比分析,分析结果表明,DBN网络诊断精度达94.83%,与浅层神经网络相比,在滚动轴承故障诊断方面具有绝对的优势。证明了DBN网络更适用于滚动轴承的故障诊断。