计及不确定性的分布式微网参与电网优化调度方法综述

谭九鼎，李帅兵*，李明澈，马喜平，康永强，董海鹰

（1.兰州交通大学 新能源与动力工程学院，兰州 730070； 2.国网甘肃省电力公司电力科学研究院，兰州 730070）

0 引言

随着我国“双碳”目标的持续推进，我国可再生能源发电产业得到了快速发展，能源系统深度脱碳势在必行［1］。以风光为主体的分布式微源作为可再生能源的重要利用载体，凭借其高效利用可再生能源、耦合多能源协同作业以及选址建设灵活等优点，成为我国构建新型电力系统，推进能源清洁低碳转型的重点研究对象。

大规模含分布式微源的微网并网给电力系统带来低价清洁电能的同时，推动电力系统演变为高不确定性的暂态稳定系统。高不确定性电力系统的负面特征重点体现在技术层面和经济层面2个方面。在技术层面，不同于传统的可控式发电设备，以风电、光为主体的分布式微源出力在短时域内具有极强的波动性和随机性，长时域内则具峰谷特性。短时域内，高比例可再生电能渗透主网将导致电网电压波形、频率等出现振荡与偏离，降低电能质量；长时域内，微源出力的峰谷特性可能导致主网供能不足或供能冗余，导致电网供能稳定性下降。

另外，分布式微网出力的不确定性对接入系统经济层面的影响也不容忽视，这些影响集中体现在对微源出力平抑过程中的调度成本上，包括功率峰谷平抑成本、频率调节成本、电压波形修正成本、储能设备控制成本以及额外添置的无功补偿设备和储能设备的成本等。

为减小以上负面影响，推动以可再生能源为供能主体的新型电力系统发展，学术界提出了基于“风-光-柴-储”微网结构的“主电网-微电网”协同调度模型，以期通过多目标协同调度，在消除分布式微源出力不确定影响的同时兼顾其他多项指标，达到精准高效控制机组启停状态及出力，平抑电网参数波动的目的。

截至目前，相关学者和从业人员对基于调度策略消除系统不确定性影响的方法进行了广泛深入的研究。本文基于现有成果，首先从确定模型、隶属度模型以及区间数据模型3个方面介绍不确定数据建模方法；在此基础上，针对各类数据模型特征分别介绍随机规划模型、模糊规划模型、鲁棒规划模型、分布式鲁棒模型4 种调度模型以及各类具体优化计算方法，总结归纳各类算法的优缺点及其适配的调度模型；最后，总结现有研究的缺陷与遇到的问题，展望微网调度方法未来的发展方向。

1 含风、光等分布式微源的微网结构

1.1 典型分布式微网结构

含可再生微源的分布式微网建设普遍遵循“源-网-荷-储”的结构［2］。微网源端结构通常由以柴油发电机等为主的可控发电设备和以光伏发电、风力发电为主的不可控发电设备构成；网层结构包括直流升压设备、DC-AC 逆变设备、变压器等传输设备；储能元件的网间功率交互特性优秀，装载于含分布式微源的微电网中，承担调控新能源电力消纳、平抑峰谷的职能；其他部件包含功率质量提升设备、无功功率补偿设备等。典型的分布式微网结构如图1所示。

由图1 可以看出，分布式微网的不确定性不仅与分布式微源的不确定性有关，还与设备故障、设备失控等不可控事件相关。相比于设备故障、设备失控等不可预测的离散型不确定事件，风光新能源微源出力总体遵循一定规律，具有一定的可预测性。分布式微源的这一特征使得通过研究其出力特征，进而辅助开展调度工作以消除大规模微网并网对接入系统产生的负面影响成为可能。

1.2 微网优化调度的主要研究目标

在电力系统中，平抑微网不确定所造成影响的本质是“主电网-微电网”结构中各设备最优出力的分配。目前，大规模以分布式微源为供能主体的微网并网对系统的影响越来越显著，研究人员从经济最优、电能质量最优、环保性最优、用户满意度最优以及多目标协同优化5 个方面开展了研究。表1 归纳和总结了当前微网不确定优化调度的主要研究目标、研究内容及特点。

表1 微网不确定优化调度研究目标、内容及特点Table 1 Objectives， research contents， and characteristics of the microgrid optimized scheduling considering uncertainties

2 微网中不确定性微源描述方法

不确定理论是以概率论、可信性理论为主体来分析无法具象描述的随机性数据的一种方法论，在电力系统和新能源发电领域应用广泛。风、光等微源出力受自然环境影响，在短时间尺度上呈间歇性与波动性，但在中、长时间尺度上输出功率曲线平滑且遵循一定的数学规律。因此，利用合理的数学模型提取功率曲线的数学特征，可使利用不确定理论表征微源成为可能。目前，含不确定性微源的微网建模方法中，主流的不确定数据建模方法主要有确定化模型法、隶属度模型法和区间模型法。

2.1 确定化模型描述法

2.1.1 概率模型描述法

概率模型是一种统计学模型，其原理是通过统计历史数据并逆求解假设模型得到模型各参数，由此提取历史数据特征。目前应用较多的概率模型为离散概率模型和连续概率模型。离散概率模型偏向描述独立离散事件的概率分布，难以与风速、光照等连续型变量适配，因此学术界普遍利用连续概率模型描述微源出力。常见的连续概率分布有正态分布、Weibull分布、瑞利分布及Beta分布等。

作为解释性强的经典方法，概率模型在表述微源出力不确定性方面有着广泛应用。文献［14］使用Weibull模型、Beta模型分别表述了风电出力和光伏出力历史数据；文献［15］使用两参数Weibull概率模型表征风电出力，使用对数正态分布表征光伏出力；文献［16］将常规发电组件、供热设备输出功率以正态分布表示，风、光出力分别由Weibull 分布和Beta分布表示；文献［17］使用多参数Weibull模型描述风电功率分布特征，提升了描述精度。

2.1.2 具象化场景描述法

具象化场景描述法的原理是用具有典型特征的具象场景替代不确定场景。目前主流的具象化场景描述法主要有随机采样法和曲线拟合法。

（1） 随机采样法。随机采样法是一种用具象化场景描述不确定参数的经典方法。该方法的原理是基于历史数据约束及概率模型约束，在不确定区间生成具体数据场景并使用该场景表示整体系统。随机采样方法中，蒙特卡洛及其衍生类方法应用最为广泛，其次是场景树模拟。传统随机采样方法难以对边缘低概率极端场景进行采样，采样得到的场景集数据特征表征能力不佳。为解决上述缺陷，相关学者开发了各类改进随机采样方法，见表2。此外，场景树法作为随机采样法的一种典型方法，是一种可视化描述不确定性问题的树形场景集结构。它将不确定问题分解成一系列细分且独立的具象化场景，场景间的支路隐含场景选取概率，指代场景在动态变化过程中的随机性，如图2所示［18］。

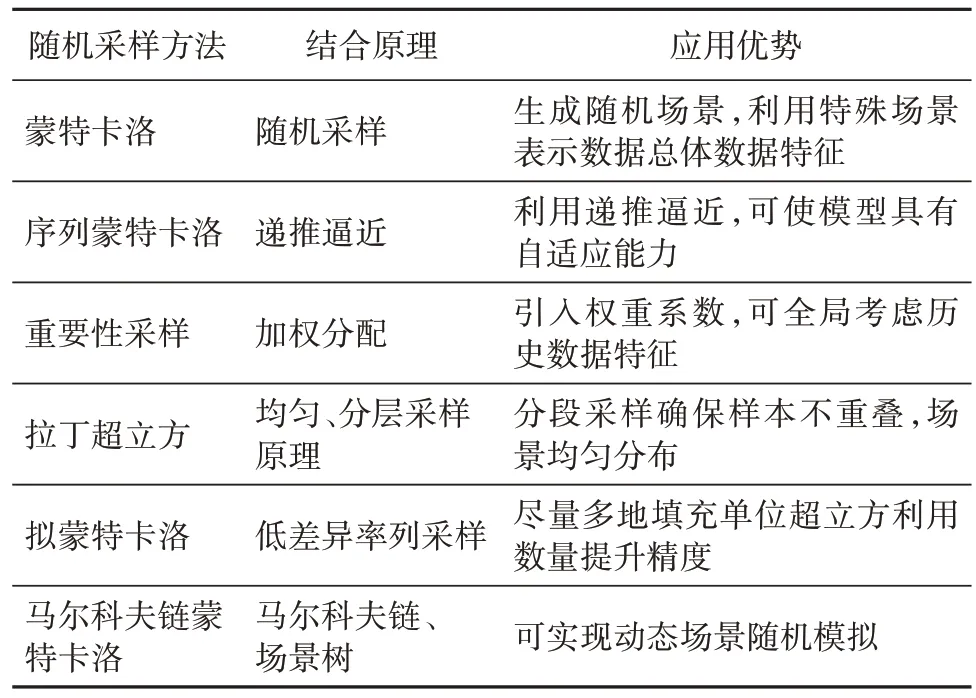
表2 随机采样方法Table 2 Random sampling methods

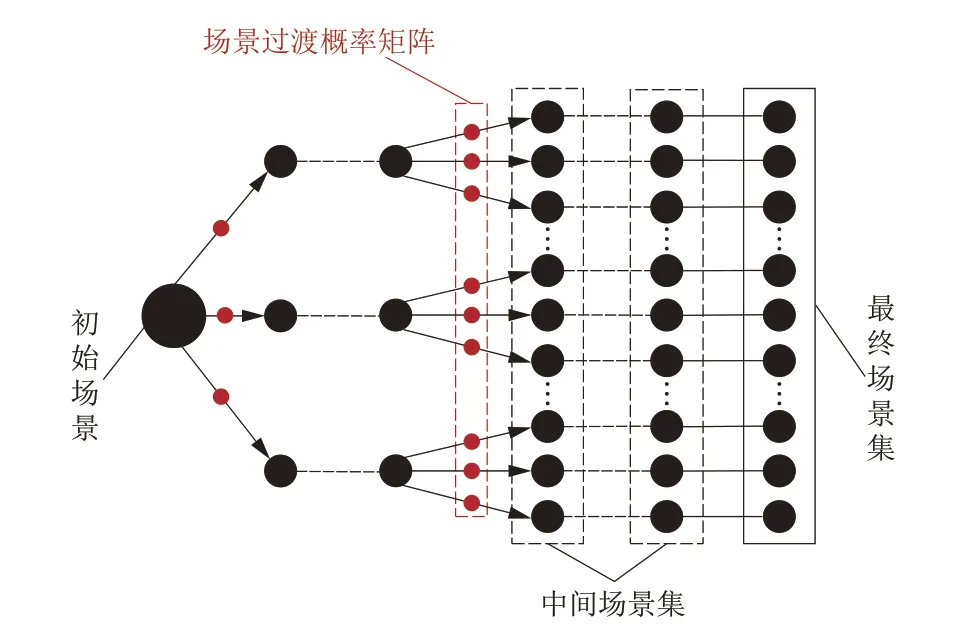
图2 场景树模拟示意Fig.2 Simulation of the scenario tree

随机采样方法在表述不确定特征方面理解性强、延展性高、应用广泛。文献［19］利用改进蒙特卡洛方法对分布式风光微源出力及负荷进行采样，基于此数据使用粒子群算法开展优化；文献［20］使用拉丁超立方采样方法在Weibull 风电功率概率模型中采样，生成风电随机场景集；文献［21］使用马尔科夫链蒙特卡洛采样方法实现动态场景集采样，生成风电功率场景序列。

（2）曲线拟合法。曲线拟合法的原理是将时间序列上独立点状场景串联成线形场景序列，用此特殊场景序列代表整体场景的数据特征［22］。传统曲线拟合使用残差平方差、残差均方根作为拟合标准。针对分布式微源出力短时波动幅度较大且数据变化非线性程度高的问题，相关学者提出基于总体噪声水平、概率密度误差、置信区间以及贝叶斯统计等来进一步精确衡量曲线拟合质量。

求解曲线拟合最优参数较为常见的方法有最小二乘法、智能优化法、确定过程法及人工神经网络法。其中，人工神经网络法由于其数据覆盖范围极广、自适应性极强和可全局优化收敛而得到广泛关注与应用。目前普遍应用的人工神经网络有反向传播（Back Propagation，BP）神经网络、递归神经网络、卷积神经网络、长短时记忆网络等。

2.2 隶属度模型描述法

隶属度模型是通过隶属度参数表征原始数据不确定程度的数据模型。隶属度模型的核心在于构建参数与目标之间的隶属度矩阵。隶属度是一个［0，1］区间内的实数，表示参数x与数集A之间的映射密切程度，隶属度越接近1 则与目标集合的关系越紧密。典型的隶属度函数有三角形函数、梯形函数、矩形函数和高斯函数［23］。表3 列举了典型隶属度函数及表达式（表中：W为微电网功率；μ为W的隶属度，0 ≤μ≤1）。

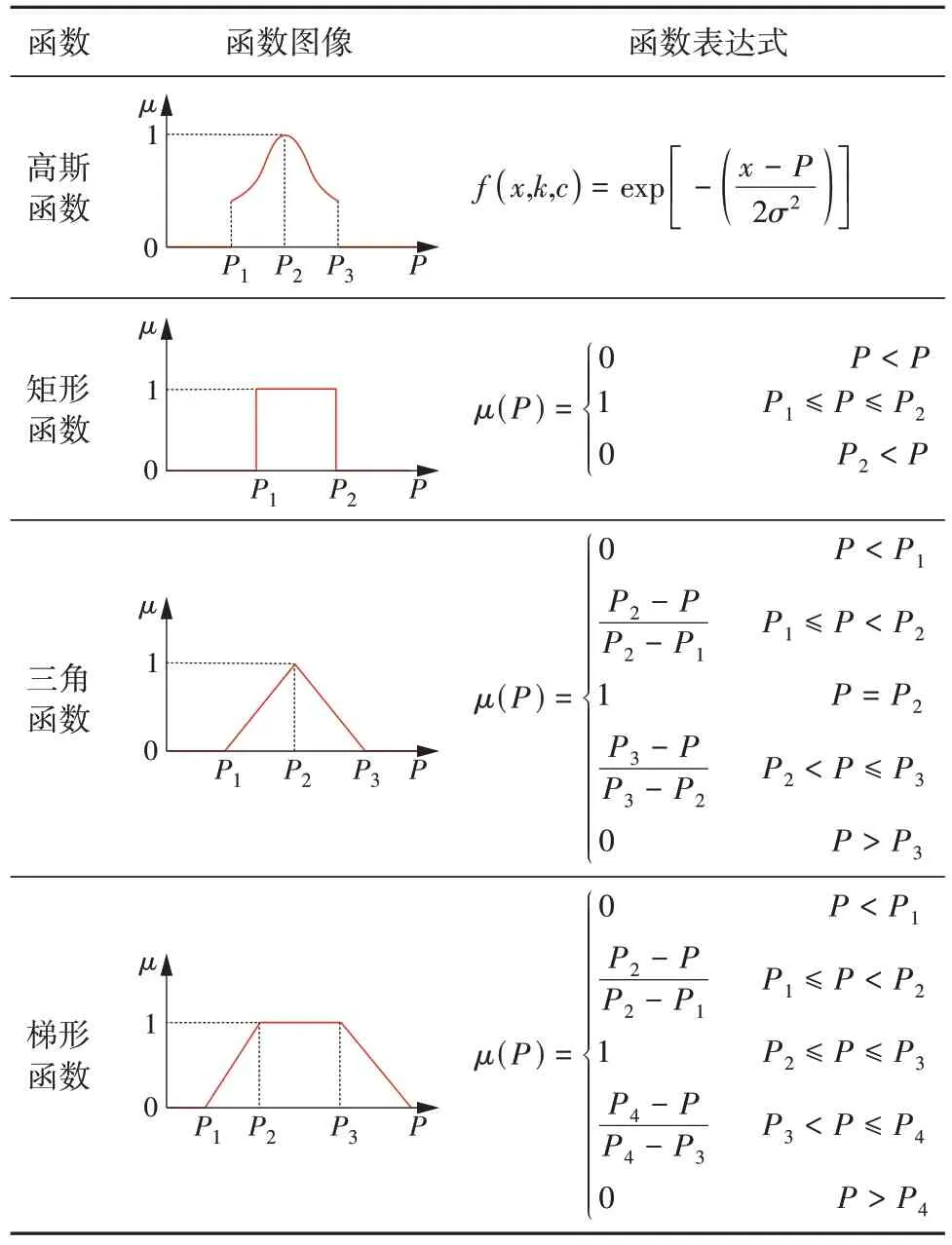
表3 典型隶属度函数及表达式Table 3 Typical membership functions and their representations

隶属度函数以隶属度为判定规则，定量描述不确定变量，这使得隶属度数据模型有极强的多参数耦合能力。从模型整体看，可构建贯穿数据源层、调度模型层、优化计算层的多层联合调度模型；从多源协同运行角度看，隶属度函数可通过调整隶属度函数交互点以自适应改变子问题耦合权重系数，从而实现多源协同调度。

2.3 鲁棒不确定集描述方法

鲁棒不确定集是由简单区间衍生出的封闭非线性参数模型。简单不确定区间利用已知数据最大值和最小值组成区间［xmin，xmax］，表征不确定参数，此区间包含一切该变量的可能取值。

基于简单不确定区间开展调度可使调度过程仅需考虑极端场景，极大提升了求解速度。但此模型得到的调度结果通常过于保守且会对边缘场景过拟合，难以综合考虑全局数据特征。因此，精细化的多边形鲁棒不确定集得到了广泛应用。

将简单不确定数区间分解为较小子集，即可得到鲁棒不确定集，目前较主流的鲁棒不确定集有盒式不确定集、多面体不确定集以及椭球不确定集3种形式［24］，如图3所示（图中：ζux，ζdx，ζuy，ζdy，分别为x轴和y轴不确定参数的期望值上、下限；Ωx，Ωy分别为x轴和y轴不确定参数的期望基值）。

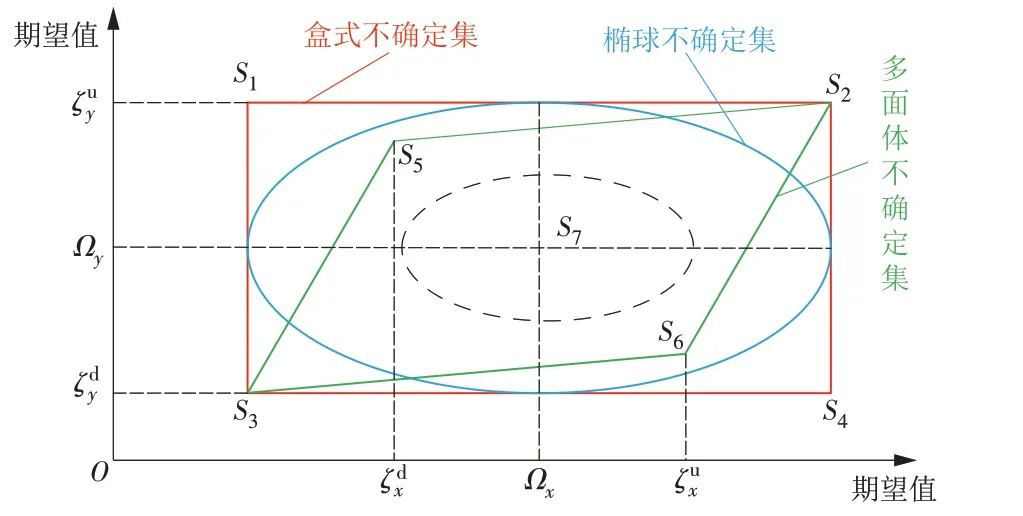
图3 鲁棒不确定集Fig.3 Robust uncertainty set

鲁棒不确定集内含大量非线性随机过程，利用鲁棒不确定集进行优化涉及凸优化模型求解，基于线性规划的常规算法难以求解。但随着以元启发算法为体系的智能算法的逐渐成熟，多目标博弈、自适应搜寻Pareto 解集成为可能。智能算法与鲁棒不确定集两者结合的鲁棒优化成为学术界研究的热点。

3 含不确定性微源的微网优化调度模型

微网调度模型是含不确定微源的微网实现多能互补、多目标优化的核心。调度模型本身并不直接进行求解，而是为优化算法提供了响应微源出力、统筹微网内设备运行约束、搜寻最优化调度解的求解平台。图4简要说明了基于调度模型的运行框架［25］。

图4 微网优化调度流程Fig.4 Optimization process of the microgrid

正确合理地选取优化调度模型，对优化算法收敛速度、算法求解精度、方案全局优化等有重要影响。基于前文对不确定数据模型的分类，可以将优化调度模型分为基于确定场景集调度的随机优化模型、利用鲁棒不确定集调度的鲁棒优化模型以及定向利用隶属度数集调度的模糊规划模型3类。

3.1 随机规划模型及其衍生模型

随机规划模型的重要特征是将不确定参数转化为随机参数，作为模型驱动数据开展调度。面对出力高度非线性的风光微源，随机规划模型通常与确定数据模型适配运行，将不确定数据转化为随机数据并基于线性约束开展调度。

随机规划模型虽然利用确定数据模型部分消除了数据不确定性带来的影响，但导致调度结果的精准度会依赖原始数据建模的准确性；此外，基于具象化场景消除参数不确定性将给模型带来巨量数据输入，使模型求解缓慢；最后，部分低概率极端场景在优化过程中难以覆盖，导致优化结果鲁棒性不足。面对以上缺陷，有学者开发了期望值随机规划模型和机会约束随机规划模型2 种衍生模型，见表4（表中：xj为决策向量；y为由x决策的目标函数；c为常数矩阵；α为约束调度结果的最大可信区间；ω为鲁棒优化和分布式鲁棒优化中表征风光不确定性的随机变量，可进一步保证调度结果收敛，不会使结果进入无解的空集状态；λ为人工权值，以精确搜索最优调度方案；g(xj)为将决策变量转换为模糊变量的模糊函数）。

表4 优化调度模型及其衍生模型Table 4 Optimization scheduling model and its derivatives

期望值随机规划模型用期望值特殊样本代表全体数据特征，最大限度减少了调度过程中的样本数据生成量。机会约束随机规划模型通过设置最大容忍度等人工约束，放大调度过程的随机搜索范围并可顾及极端场景，保证调度结果的鲁棒性。

目前，随机规划模型的应用与改进侧重于准确表述驱动数据、构建求解高效的约束条件2个方面。例如：文献［26］使用常规场景树模拟风光电功率序列，在随机规划模型中则构建了风光微源功率的二阶锥约束，高效求解了调度成本最优的优化目标；文献［27］以可再生能源出力预测误差、可变负荷功率以及随机停电为机会约束条件，利用线性求解方法求解，在有效削减随机采样数据规模的同时提升了日前调度的计算效率与调度精度，相较于蒙特卡洛随机采样方法更具应用优势。

3.2 鲁棒规划模型

鲁棒规划模型基于鲁棒不确定集数据模型，依据悲观决策准则展开调度，抗风险抗波动能力极强。对于含风、光等微源的微网，鲁棒规划模型仅需提取风光微源出力区间即可开展调度，进一步减少了调度过程中数据的采集量。

鲁棒规划模型作为近年来最热门的优化方法，在微网优化调度应用方面还存在一些缺点。一方面是调度结果鲁棒性侧重过强，导致结果保守；另一方面是鲁棒模型求解通常为复杂的非线性问题求解，求解时需要将问题转化为具有多项式计算复杂度的凸优化问题［28］，求解过程复杂繁琐。

为弥补以上缺陷，业内学者提出了结合动态优化算法的分段式求解模型以提升求解效率，并引入自适应原理避免结果过度保守。文献［29］为降低调度结果的保守性，构建了多重不确定等级对目标分别评定，并结合自适应原理实现动态经济最优目标优化。文献［30］在鲁棒模型中引入自适应原则，既保留了鲁棒调度结果的保守性，又提升了Pareto解集逼近能力。文献［31］将鲁棒模型与动态优化算法结合，构建了多时段、多对象的多阶鲁棒模型，再利用动态优化算法分段求解，有效提升了模型的求解效率。

3.3 分布式鲁棒规划模型

相较于传统鲁棒模型，分布式鲁棒模型考虑了随机变量概率分布的特征，在优化结果保守性方面有一定改善。目前，分布式鲁棒模型构建的主要方向是基于矩信息的分布式鲁棒和基于概率距离的分布式鲁棒2种。

分布式鲁棒模型通过提取参数矩信息达到描述不确定参数概率分布的目的。应用较多的矩信息包含均值（一阶矩）、方差或散度（二阶矩）、斜率（三阶矩）；基于信息掌握程度可再细分为基于确定矩的分布式鲁棒规划模型和基于不确定矩的分布式鲁棒模型。基于概率距离的分布式鲁棒模型通常采用凯利离散度（Kullback-Leibler Divergence，KL）、Wasserstein 距离等概率距离描述参数分布特征。

为进一步精简分布式鲁棒模型的计算流程，兼顾提升模型多目标调度的效能，业内学者提出了结合多阶规划模型的分布式鲁棒模型并得到了广泛应用。文献［32］在分布式鲁棒模型中引入风险价值理论并利用多阶规划方法求解目标函数。文献［33］构建了多阶分布式鲁棒规划模型，第1 阶段确定风电容量分配决策，第2 阶段确定运行决策。考虑线性算法在计算速率上的优势，文献［34］在构建多阶鲁棒模型开展调度的同时，利用线性列和约束生成（Column and Constraint Generation，C&CG）算法求解模型经济最优目标，有效提升了模型的运行效率。

3.4 模糊规划模型

模糊规划模型是定向利用隶属度数据模型开展调度的规划模型。由于隶属度模型能定量描述原始数据关联程度、多目标耦合程度等模糊参数特征，因此，模糊规划模型具有极高的灵活性和数据耦合能力。以上数据特征令模糊规划模型在多能流互补调度、长短时时域规划、多目标协同优化等应用场景中具有突出优势。

实际应用过程中模糊规划模型也存在一些缺点：一方面，模糊规划模型中隶属度函数的选取暂无体系学说，导致模型调度过程始终具有一定误差；另一方面，模糊规划模型具有静态性，自适应能力不足，面对动态随机性强的风光微源出力序列，其精准调整系数能力不足。

模糊规划模型因多目标表述能力较好，通常与综合能源系统的多能互补调度工作相结合。在系统各电源耦合协同供能方面，文献［35］利用隶属度函数表征光热、光电、风电多能流的耦合程度，形成多源耦合协同调度模型。在系统多目标协同优化方面，文献［36］设定隶属度μ为子问题耦合比例系数，解决了动态多目标优化问题中子问题重要性自适应分配问题。文献［37］用隶属度函数表示风电机组出力、功率爬坡持续时间，再利用隶属度表示最优解与目标函数值之间的关系，实现了调度过程全隶属度化。在多电源耦合方面，文献［38］利用隶属度函数建立墨西哥东部的局部风电场与水电厂联合模糊规划模型并开展经济优化调度。另外，为解决隶属度函数动态修正能力较差的问题，文献［39］在模糊规划模型中引入自适应指标，使模型能基于历史数据自行调整隶属度。

4 微网优化调度求解方法

研究表明，电力调度优化问题实质上是优化规划问题［40］，根据各类调度模型的分类，具体优化算法如图5所示，各优化调度算法的特点见表5［41］。

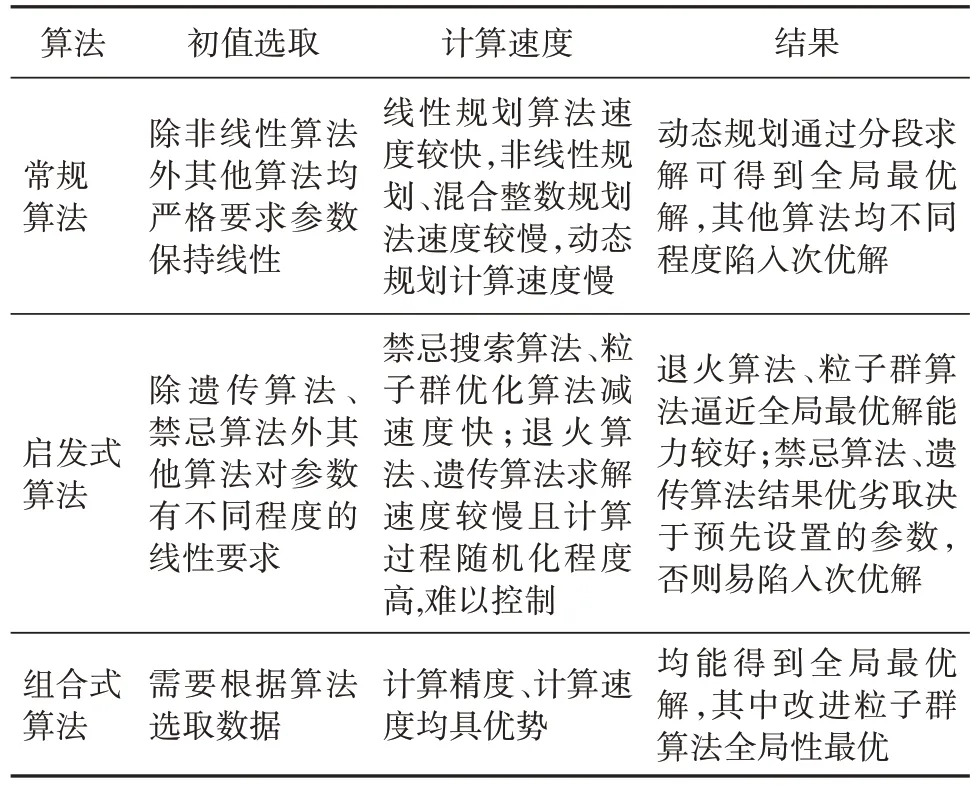
表5 优化调度算法对比［41］Table 5 Comparison of different optimization dispatching algorithms［41］

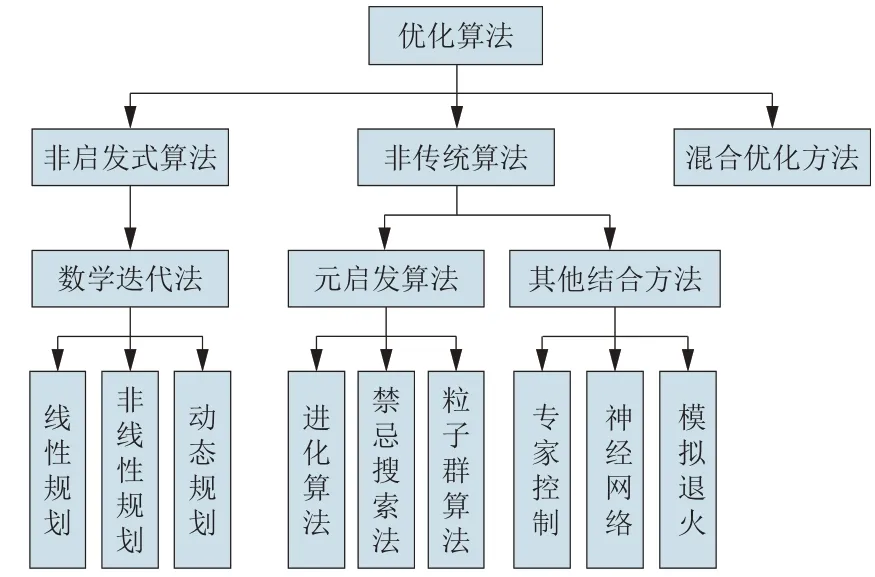
图5 优化算法树状图Fig.5 Optimization algorithm tree diagram

4.1 常规优化算法

常规优化算法包括线性优化算法及其衍生算法，其中衍生算法以传统线性算法为基础，结合迭代、整数规划等原理构建而成。目前，应用广泛的优化算法有线性规划、非线性规划、混合整数规划、动态规划等，见表6。

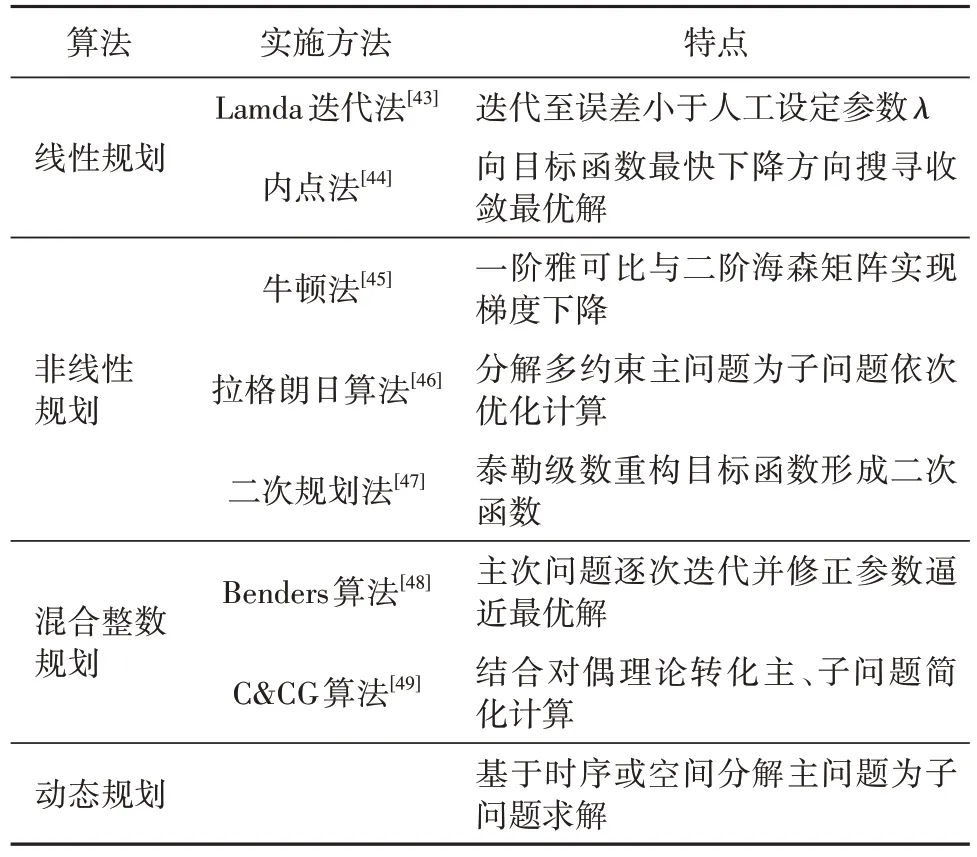
表6 常规优化算法［42］Table 6 Regular optimization model and its derivatives［42］

常规优化算法结构简单、计算流程理解性强且应用广泛，但面向微源为主的不确定数据源，还需考虑额外线性化步骤初始化参数，因此常规算法在开展优化调度时通常与确定性数据模型相结合使用。文献［50］是典型常规算法在调度方面的应用，首先将不确定参数线性化，然后构建随机规划模型并通过线性规划方法求解，实现了风电不确定波动的无功优化调度。

在实际应用方面，目前有将鲁棒不确定集与常规算法相结合的案例。文献［51］设定㶲效率指标来评估调度质量，构建了多阶目标函数，开展多目标区间线性规划调度；文献［52］采用区间模型描述风光微源出力的不确定性，随后利用区间线性规划法求解效益最大化的日前调度方案。上述文献基本实现了调度质量最优前提下的调度成本最优，但总体优化效果不够理想。

综上所述，常规算法在面向线性条件约束的凸优化问题求解方面具有良好的泛化性能、准确性和快速性，但在处理非线性的风光微源出力约束、非凸多目标问题时，常规算法求解过程复杂且结果全局最优性较差。学界试图通过引入鲁棒区间变量提升参数线性化指标，构造多阶调度算法等人工因子来改进常规优化算法。另外，以Benders 分解算法（Benders Decomposition Algorithm）［48］和C&CG 算法［49］为代表的混合整数规划方法，以分段式优化方法为代表的动态规划方法也在微网优化调度方面得到了应用。

4.2 多目标启发式算法

在微网调度多目标优化方面，已有方法主要分为多个目标协同优化和将多目标汇集为单目标优化的2 类方法。传统非启发式优化算法应对以上2种模式的自适应效果均不理想，且在高维约束条件内开展自搜寻逼近优化解集的能力有限，因此，多目标优化算法更多采用启发式优化算法。

启发式优化算法是一种群体智能算法，求解步骤为：（1）基于设定规则生成大规模满足约束超空间的个体；（2）个体在约束超空间内随机运动，模拟搜寻并选取相对最优个体；（3）选取并令下一子代“继承”局部最优解特征，再次随机运动；（4）迭代逼近最优解集。不难看出，启发式算法不需要约束条件或输入参数严格线性化，求解过程为非线性的随机过程，面对多目标协同求解时不会陷入不收敛的情况，对多目标求解适配性较强。

目前较主流的启发式算法有粒子群算法［53］、进化算法、禁忌搜索算法、帝国算法等。为提升算法效能，启发式算法通常与退火算法、专家系统、神经网络［54］等方法相结合，形成了启发式混合优化算法。启发式算法及其混合算法以其优秀的优化效果以及强适配性，得到了学术界的广泛应用。

启发式算法及其混合算法在处理各类优化问题时性能良好，但构建流程复杂，计算过程可控性相对较差，因此需考虑基础数据、模型种类的实际情况选取具体算法。如文献［4］结合遗传算法交叉变异原理改进粒子群算法实现最优解集搜寻，得到了最优多目标Pareto 解集；文献［8］采用NSGA-II 求解系统节点电压降、碳排放、网损的多目标解。

5 结论与展望

利用分布式微网“源-网-荷-储”结构与主电网交互消除微网不确定性的调度策略在平抑精度、响应速度以及多目标联合优化等方面具有突出优势，得到了广泛且深入的研究与应用，但在实践过程中许多技术问题也逐渐显现。

首先，传统IEEE模型难以对接入分布式微源的节点进行定义和分类，出力随机性极强的分布式微源将使IEEE模型的潮流分布不确定程度上升，导致电网调度困难；其次，目前研究的配电网局限于辐射状或带状节点模型，但现实中电网更多为网状且具有局部环流和孤岛节点，如何建立具有普适性的配电网约束模型是学术界的研究重点；然后，如何精准高效地实时预测风光可再生能源出力，以实现较高新能源消纳率的日内调度是一个亟待解决的学科问题；最后，微网调度模型需要在高效响应不确定参数变动、精准迅速完成调度方面进一步发展与提升。为响应上述需求和解决相关问题，未来微网调度方法研究将围绕着以下几点展开。

（1）储能设备作为“削峰填谷”的核心设备，在平抑风、光等分布式电源出力波动方面起到了重要支撑作用，但微电网优化调度中反映储能设备真实出力特征的模型相对匮乏，对储能设备电气潮流方向过于理想化。未来对于储能设备的建模将一方面集中于储能设备出力特征，另一方面在于构建可真实反映储能设备在微电网中运行状态的精确控制模型。

（2）随着微电网优化目标的多样化与原始数据的多维化，开发可深度挖掘原始数据特征的多目标智能优化算法以应对复杂的调度场景，将成为未来发展的一个主要方向。微电网优化调度算法总体向模糊数据处理方向发展，预计未来算法在数据处理方面将向着自主化修正、无监督学习的自适应方向发展，智能化程度高、自主性强的算法将逐渐取代传统人工设定规则的调度方法；另外，如何将算法与以上模型结合生成对抗网络，将新一代数据驱动技术与现有模型结合是未来算法发展的重要方向。

（3）建立具有普遍应用价值的含分布式微源接入的IEEE 模型，对精确描述调度对象和实现高精度、高效率日内实时主动配电调度有着重要推动作用。目前应用较为广泛的基于节点法和支路法的潮流计算方法难以应对具有随机性的电网模型，传统节点分类方式也难以对模型各节点进行分类。目前，学者研究重点集中在电网重构和网内多节点交互模型上，旨在构建能够表征潮流环流和潮流孤岛场景的IEEE模型和精准快速开展潮流计算算法。

（4）构建电气化交通与分布式微网的融合供能体系需求旺盛。电动汽车（Electrical Vehicle， EV）近年来保有量大幅上涨，持续稳定向EV 供能的同时保证电网稳定成为一项新挑战。相较于一般储能设备， EV 负荷的时空分布随机性更强， EV 电池也不具备一般储能设备的统一电池容量水平，将导致各充电节点负荷功率不统一；另外，EV 电池与电网具有双向互动特性，部分负荷节点会向着供能节点转变。以上现象将增加分布式微网的不确定性，加剧微网潮流混乱，因此，建立考虑EV 设备接入的微网模型具有重要现实意义。