路网耦合下计及电动汽车V2G潜力的充电站选址定容研究

孙雨乐，漆淘懿a，，赵宇明，叶承晋a*，惠红勋

（1.浙江大学 a.电气工程学院；b.工程师学院，杭州 310027； 2.澳门大学 智慧城市物联网国家重点实验室，澳门999078； 3.深圳供电局有限公司，广东 深圳 518020）

0 引言

在能源安全和“双碳”目标的双重驱动背景下，我国将电动汽车（Electric Vehicle，EV）的发展作为交通能源转型的重要战略［1-2］。国际能源署（International Energy Agency，IEA）在《2021 年全球电动汽车展望报告》中指出，全球EV 保有量截至2020年已超过1 100万辆，中国以约550万辆的存量成为全球最大市场［3］。

为满足新增电动汽车的充电需求，电动汽车充电站的选址定容问题成为一个值得研究的重要问题。电动汽车作为大功率、随机性的冲击负荷，若其大量且无序地接入电网，可能会导致电网线路阻塞、电压越限、网损增加等多重问题［4-5］。与此同时，电动汽车又兼具储能特性。当电网中负荷过高时，可以利用电动汽车向电网进行放电，充当电力系统中的电源；当电网中负荷较低时，可以利用电动汽车进行充电，储存电网中过剩的电量，减少电能浪费，这种方式被称为电动汽车的车辆到电网（Vehicle to Grid， V2G）技术［6］。通过上述网荷互动方式，不仅可以缓解电网效率低、可再生能源波动等运行问题，还可以为用户创造额外的收益［7-8］。因此，通过合理规划充电站的位置，优化不同地点、不同时段电动汽车储能调节潜力显得尤为重要。近年来网约车数量激增，其中大部分都是电动汽车。本文以电动网约车为例，探索其对充电桩分布的影响。

近年来对于电动汽车V2G 技术的研究较多，文献［9］针对V2G 在工作时造成的谐波含量高、功率因数低等问题，对充电桩内部电路进行重新设计以提高电网质量。文献［10］基于模糊控制的改进比例谐振控制技术，进一步提高了电力系统的稳定性和动态性能。上述研究通过电力电子技术对V2G技术进行控制与优化。文献［11］应用整数规划求解电动汽车充放电两阶段优化模型，以有效降低峰荷并平滑负荷曲线。文献［12］针对调峰控制策略，运用粒子群优化算法对电动汽车的充放电功率进行优化。以上文献都是从电动汽车储能特性与电网互动角度进行研究，探索电动汽车V2G 技术如何更好地进行削峰填谷、提高电网稳定性。

由此可见电动汽车V2G 技术具有极强的利用价值。但是现有研究多基于充电站的位置确定的情况，同时对于交通网络中车流量的分布考虑仍不足，由此可能造成模型不够准确。现有对于充电站规划的研究中，文献［13］综合考虑充电站的经济运行和车辆动态功率模型进行充电站规划，文献［14］根据电动汽车的充电需求，结合投资商的意愿对充电站进行选址定容。以上研究均是针对社会投资的充电站，这部分充电站总是以最优的经济效益作为选址的重要指标。然而，对于电网投资建设的充电站，其具有一定的公共属性，是根据相关政策要求的车桩比，随着电动汽车数量增加而必须建设的。这部分充电桩在建设时无需考虑建设投资成本。除了满足车主充电需求，通过合理规划充电站，提高充电站拥有利用率、最大化电动汽车V2G调节潜力也是需要考虑的重要因素。因此，本文从城市规划角度出发，充分考虑电动汽车在路网中的分布情况，以电网建设的充电站为例，提出了计及电动汽车V2G 潜力的充电站选址定容方法，为电网公司提供参考，以获得最好的社会效益。首先，构建交通网并通过Floyd 算法对电动汽车的行驶路径进行模拟，预测出充电负荷的时空分布。然后，从所有网络节点中分时段求取最优位置，使所选充电站在满足路网中所有电动汽车充电需求的同时，最大化电网可用的储能容量。其次，根据各时段的充电站选择综合分析，求出适合全时段的充电站位置，并根据各时段的停车需求确定每个充电站的充电桩数量。

最后，以某市辖区路网拓扑结构为例，对所提出的模型进行验证。结果表明，所提方法对城市电网投资的充电站选址定容规划具有一定的指导意义。

1 计及用户习惯的电动汽车储能建模

1.1 电动汽车使用习惯建模

电动汽车车主的行为习惯决定了电动汽车的日行驶里程、起始充电时刻、停车时间以及起始充电的电量，是影响储能容量计算的关键因素。电动汽车一般分为电动私家车、电动商务车、电动公交车、电动网约车和出租车4大类［15］。近年来，网约车数量激增，在城市交通运输市场中的比例不断增加。截至2022 年1 月，各地共发放网约车驾驶员证398.8 万本、车辆运输证158.3 万本；1 月份订单总量达到70 420.3 万单［16］。因此，可以认为网约车已经成为交通网中不可或缺的重要组成部分，具有广阔的研究前景。

日行驶里程反映电动汽车在1天内使用多少电量，进而影响目的地的预测。通过拟合可以得到日行驶里程的概率密度函数为

式中：s为每天电动汽车行驶的路程，km；μD和σD分别为函数的期望值和标准差。

电动网约车的出行时刻由工作时间、出行习惯决定，其典型的出行时间的概率分布如图1所示。

电动网约车的出行主要集中在白天，使用量较大的时段为08：00—21：00，因此可以认为电动网约车的出行时刻高峰时段为06：00—08：00［17］，根据文献［18］中提供的函数拟合数据，可以得到电动网约车的出行时刻满足的分布概率为

式 中：λ1= 0.389，α1= 7.046，β1= 1.086，λ2=0.066，α2= 15.610，β2= 9.667。

同时，电动网约车的停车时间、初始电量也具备一定的随机性，与车主的用车习惯以及车辆用途也有着密切关系。从大数据统计角度来看，可以认为电动网约车的分布服从正态分布［19］。正态分布的概率密度函数为

式中：T为电动网约车的停车时间，h；μ为均值；σ为标准差。

1.2 聚合电动汽车V2G储能潜力建模

电动汽车能够提供的V2G 储能容量与电动汽车的数量，电动汽车的状态（汽车的起始荷电状态（State of Charge， SOC）、电动汽车的功率、工作效率、百公里耗电量等）、车主的用车习惯（车辆的出发时间、停车时间）有关。

首先对储能容量的可利用服务时间进行建模。假设在电动汽车作为储能参与调节的过程中都采用恒功率模式，单辆电动汽车可持续服务的时间为

式中：Tch，Tdis分别为单辆电动汽车参与储能的充电时间放电时间；SOCn(ti)为ti时刻第n辆汽车的电池荷电状态；SOCch为参与储能的电动汽车期望达到的充电电量；SOCdis为预留出行的能量比；Ebat，n为第n辆电动汽车的电池可用容量；Pch，n，Pdis，n与ηch，n，ηdis，n分别为第n辆电动汽车的充放电功率和充放电效率。基于电动汽车的可用服务时间，并对车辆数进行累加，可以求得聚合储能容量。本文将多个电动汽车的V2G 储能进行整体聚合，计算全部储能容量。在调度优化计算时只需要一个集中的充放电变量，包括电动汽车的充放电功率以及可用的储能容量，具体聚合过程如下。

1.2.1 电动汽车接入充电桩的总功率

式中：Pch，total，t，Pdis，total，t分别为t时刻电动汽车总的充电、放电功率；λ为车辆的充放电状态。

1.2.2 电动汽车总可用储能容量

基于单辆的电动汽车储能容量进行求解，对一定时间段内的单辆电动汽车储能容量进行累加，可以得到时间段内可用的总的储能总量。计算公式为

式中：Etotal，ch(T)，Etotal，dis(T)为时间段T内的可用储能容量总和；t1和t2为时间段T的起始时间和结束时间；N为参与调度的电动汽车数量。

此外，电动汽车的充电速度不应超过其最大充电功率的限制，放电速度不应超过电动汽车的额定功率。其表达式为

式中：Pn，ch，t，max，Pn，dis，t，max分别为第n辆电动汽车在t时刻的最大充电功率和额定放电功率。

2 计及动态车流的交通网模型与目标函数的建立

2.1 动态交通网模型

在已有电动汽车与电网交互的研究中，一般采用静态交通网模型进行研究，交通流量并非随时间而改变。为了进一步细化储能的计算方法，本文构建动态交通网模型，将一天分为7 个时间段（早高峰、上午、午间、下午、晚高峰、晚间、其余时段）根据时间变动更新每个时段的路段流量，动态交通网模型可以表示为

式中：G为交通网集合；V为交通网中所有节点的集合，共有u个；E为交通网中路段的集合；H为划分的时间段集合，T= 7；K为路段的权重集合；vi为交通网中第i个节点；vij为连接第i个节点和第j个交通网节点的路段；kij(t)为t时段内路段vij的权值。交通网集合G中各节点间的连接关系用邻接矩阵D来描述。矩阵D的元素dij的表达式为

道路拓扑结构如图2 所示，其生成的矩阵D如式（15）所示。

图2 道路拓扑结构示例Fig.2 Topology of the test roads

在出行过程中，电动汽车车主往往最关心车辆的行驶时间，而行驶时间与行驶路程与行驶速度密切相关。一般来说，行驶路程在确定路线后较容易获取，是一个静态常量；行驶速度则与道路的容量，车流量等因素密切相关，是一个动态变量。故本文引入速度-流量模型计算车辆行驶速度，进而方便计算总行程需要的时间。电动汽车行驶速度vij表达式为［20］

式中：vij.max为路段ij规定的最高行驶速度；Cij为路段ij的通行能力，由道路等级决定；Qij(t)为t时刻路段ij的车流量；Qij(t)与Cij的比值为t时刻路段的饱和度；a，b，γ为道路的自适应系数，由道路的等级确定。

2.2 路径选择模型

通过模拟电动汽车的行驶路径，能更好地预测出电动汽车充电负荷的时空分布，这是充电站规划的必要条件。

2.2.1 网络节点关系（OD）分析法

2.2.2 Floyd算法

目前现有的路径选择算法基本分为Dijkstra 算法与Floyd 算法［22］。Dijkstra 算法能够解决从某一点出发到其他各点的最短路径选择问题，因此是一种能够解决有向图和无向图的单源最短路径问题［23］。Floyd算法是典型的多源最短路径算法，又称为插点法，是一种用于寻找给定的加权图中多源点之间最短路径的算法。主要特点是需要用邻接矩阵来储存边，并通过考虑最佳子路径来得到最佳路径［24-27］。2 种算法各有优劣，相比较而言，首先，Dijkstra 算法不能处理负权图，即每条道路的权重值必须是正数才可使用，而Floyd 算法可以，算法适用范围更广。其次，Dijkstra 算法更适合处理单源最短路径，Floyd算法更适合处理多源最短路径。就本文而言，由于本文需要处理多源路径，同时为了降低编程难度，因此Floyd算法更加适合。

Floyd算法用于求取两点之间的最短路径，算法的基本思想是通过迭代地比较所有可能的路径，从而找到图中任意两个节点之间的最短路径。其算法流程图如图3所示。

图3 Floyd算法流程Fig.3 Floyd algorithm

首先，对于生成的目的节点和起始节点，最终目标是求出到达目的地行驶最短时间与行驶路径。在本文研究中，首先根据选定道路的路程与对应道路的行驶速度可以计算出每条道路的行驶时间，设置起始节点与目的节点初始的最短时间为它们之间连接道路的行驶时间，如果2 个节点之间没有道路相连，则设置为无穷大。

然后，通过对所有可能的中间节点进行遍历，依次考虑每个节点作为中间节点时，是否可以通过这个节点缩短行驶时间。对于每一对节点i和j，以及每一个中间节点r，比较当前的最短时间和通过节点r的时间之和是否更短。如果更短，则更新最短时间以及路径中的中间节点。通过多次迭代，不断更新最短时间和路径中的中间节点，直到所有的节点都被作为中间节点考虑过。

最终，得到了每一对节点之间的最短时间和行驶路径，根据这一信息可以模拟电动汽车的行驶路径，从而进行充电站的选址定容研究。

本文通过OD 分析法模拟电动汽车的行驶路径。电动汽车的初始位置由统计数据给定，通过OD 分析法确定电动汽车的目的地。确定出发地和目的地后运用Floyd 算法求解最短路径。车辆到达所选目的地后，将此目的地视为下一次行程的出发地，同时通过OD 分析法再次确定下一次行程的目的地，重复以上过程即可不断模拟电动汽车行驶路线。

2.3 目标函数建立

根据交通网节点和电网节点的数量确定目标的充电站数量，通过对充电站和充电桩进行合理规划可以有效缓解道路压力和增强电网的承载力。

从交通网角度，为缓解道路压力，期望电动汽车能在每个充电站平均分布。为衡量这一指标，引入方差对数据进行处理。

式中：S为计算出的方差；Xcar，i为第i个充电站中电动汽车的数量；Xˉcar，i为需要充电的电动汽车在所有充电站内平均分布时每个充电站的车辆数；Nst为充电站的总数量。

从电网角度，期望能提供更多的储能容量以供调度，因此引入式（9）、式（10）储能的计算方法，同时认为车辆在充满电后停车时间越久，所提供的储能可供调度的时间就越久。

由于所得的各项数据指标数量级不相同，但认为其在充电站的选址定容研究中重要性是相同的，为使数据具有可比性，将所有指标归一化处理，将数据等比缩小或放大至0～1 的区间内，方便进一步计算。根据电动汽车V2G 储能潜力、停车时长、电动汽车在充电站内平均分布3 个指标，结合式（9）、式（10）、式（4）、式（18），目标函数为

式中：Etotal，ch，gy(T)，Etotal，dis，gy(T)为归一化后充电、放电状态下的电动汽车储能总容量；Ti，gy表示归一化后第i辆电动汽车充满后的停车时间；Nfull表示在研究的时间段内可以充满电的电动汽车数量；表示归一化后充电站电动汽车分布的方差。

3 算例分析

3.1 仿真参数设置

3.1.1 电动网约车参数设置

根据文献［18］，某市某区电动网约车数量为5 500 辆；电动网约车主要使用类型为比亚迪E6，其主要参数：充电功率为45 kW，电池容量为83 kW·h，百千米电耗为20.5 kW·h；由1.1 节可知电动汽车的出行时刻、停车时间等行驶参数；由2.1节动态交通网模型，并考虑城市交通网结构的复杂性和电动汽车的行驶特性，本次建模分析过程中将电动汽车的行驶速度定为60 km/h，并认为电动汽车按照最短路径匀速行驶。

3.1.2 交通网结构设置以及道路设置

为验证本文充电站选址定容模型的有效性，选取已进行城市功能区划分的某市辖区交通网拓扑结构如图4所示［18］，该交通网包含29个节点和49条道路，节点即为道路的相交处。各道路的长度、流量、各时段饱和度数据见参考文献［21］。该区域分为居民区1（含节点1—11）、居民区2（含节点12—16）、工作区（含节点17—20）、商业区（含节点21—29）。本文将道路等级分为主干道和次干道，参考文献［21］的试验数据，对于主干道，a，b，γ分别取值1.726，3.150和3.000；对于次干道，a，b，γ分别取值2.076，2.870和3.000。

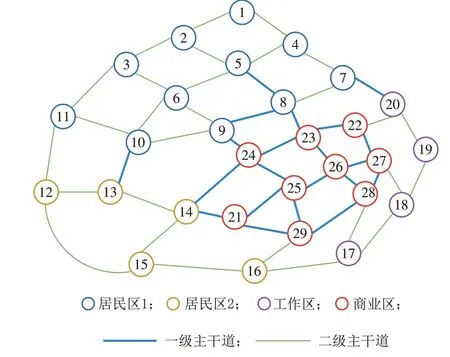
图4 测试区域部分主干道网路示意Fig.4 Traffic network in the test urban area

3.1.3 初始出行位置、初始电量与停车时间

不同的功能区作为出行位置的概率不尽相同，一般来说，电动网约车每天的工作分布在全市的各个区域，其分布数据见文献［18］，其数据如图5 所示。对应函数式（1）中：μD=3.20，σD= 0.88，0 ＜s＜200。

图5 电动汽车初始出行位置分布Fig.5 Distribution of electric vehicles' departure locations

电动汽车的初始电量与停车时间均认为服从正态分布，用tpark表示电动汽车的停车时间，tpark～N(2.0，0.3332)，其服从期望值为2，标准差为0.333的正态分布；用SOCbegin表示电动汽车的初始电量，SOCbegin～N(0.8，0.1672)，其服从期望值为0.8，标准差为0.167的正态分布。

3.1.4 研究时间段

本文以夏天为背景，考虑一天中09：00—19：00的储能容量情况。同时认为这10 h 段内为负荷高峰时段，因此只考虑电动汽车放电储能容量，忽略电动汽车充电储能容量。

3.1.5 电网与充电站数量设置

本文选用IEEE 14 标准节点，根据电网节点数量，选取5个节点作为充电桩进行计算。IEEE 14标准节点结构如图6所示。

图6 IEEE 14标准节点结构Fig.6 IEEE 14 standard node structure

3.2 最优充电桩分布

本算例基于Matlab 平台对算例进行分析与求解。在本次计算中，将09：00—19：00 分为4 个时段（09：00—12：00，12：00—14：00，14：00—17：00，17：00—19：00）进行研究，首先求出每个时段的最优充电站分布情况以及2 个次优情况，然后根据12种结果中的充电站分布进行统计与分析。各时段最优充电站选址节点分布情况见表1。

表1 各时段最优充电站选址节点分布情况Table 1 Distribution of optimal charging station sites in various periods

各时段的最优充电站选址节点统计饼状图如图7 所示，在所有时间段中，一共有17 个节点被选为最优节点，占所有节点的58.6%。其中，14 号节点被选中14 次，占比18.7%；20 号节点被选中13次，占比17.3%，此2 个节点可以认为是最优的充电站选址位置。26，8，25号节点分别被选中9，7，7次，占比12.0%，9.3%，9.3%，这3个节点可以认为是充电站选址的次优位置。14，20，26，8，25 这5 个节点被认为是最优节点的次数最多，因此认为这5 个节点是最优的选址定容位置。最优充电站分布如图8所示。

图8 最优充电站分布Fig.8 Distribution of optimal charging station sites

最优的充电站分布中8，14，20 这3 个充电站位于商业区与工作区、商业区与居民区的交界点处，25，26 两个充电站位于商业区的中心。这从侧面说明商业区的车辆量大、充电需求频繁，同时也说明商业区与其他区域经常有车辆的交互。其他被选中的节点（如9，23 等）也多数位于功能区的交界处或者是商业区内部。

为确定充电站的充电桩容量，在确定充电站的具体位置后，重新研究分析这5 个节点在各个时段的储能容量、可用时间、车辆分布，如图9—11所示。

图9 最优分布下各时段充电车辆分布情况Fig.9 Distribution of charging vehicles in various periods under the optimal distribution

图10 最优分布下各时段各充电站可用时长Fig.10 Available hours at each charging station in various periods under the optimal distribution

图11 最优分布下各时段储能容量Fig.11 Energy storage capacities in various periods under the optimal distribution

从3 种数据的分布情况可以看出，充电负荷的高峰时段都出现在09：00—12：00 与17：00—19：00时间段，在12：00—17：00 时间段内，充电需求会出现一个低谷。预测结果与文献［21］结果一致。其中8 号节点全时段的车辆充电需求最大，这一节点由3 条一级主干道以及一条次级主干道相连，连接最大的生活区以及商业区。从图中可以看出，在这一节点处所产生的储能容量与可用时长也最大，是所有充电站中最繁忙的充电站。26 号节点其次，作为商业区的中心，其所能提供的储能容量也十分可观。14，20，25 号节点的容量与可提供的服务时间近似。从时间角度来看，09：00—12：00 这段时间的充电需求最大，17：00—19：00时间段其次。

根据电动汽车的已知数据，每辆电动汽车从0%充电至100%的时间约为2 h，而时间段也近似以2 小时进行划分，因此可以认为每个时间段内的充电汽车数量即为该时段所需要的充电桩数量。充电桩的规划以满足所有时段下车辆抵达电站时无须等待可以立即开始充电为目标。因此，充电站中充电桩的设定就以图9中电动汽车在所有时间段中的最大值作为充电桩的安装数量。结合以上分析，给出本次充电站的选址定容的最优结论，见表2。

表2 最优充电站选址定容情况Table 2 Optimal charging station location and capacity

其中，储能的容量和可利用时长考虑的时间段为09：00—19：00，由于大部分车辆的出行都在这一时间区间之内，可以认为对这一时段的研究代表全天的情况。

4 结束语

本文提出一种考虑储能容量的电网投资的充电站选址定容模型，并以某市主城区的部分交通网和IEEE14 节点配电网为例，验证了方法的有效性。结果表明：

（1）充电站的最优位置多数分布在商业区和生活区的交界处，以及商业区的中心。同时在充电站附近一般有2条及以上的一级主干道。说明在生活区和商业区间车辆交往密切，商业区的充电需求较大，充电站分布具有极强的地域特性。在这一区域建立充电站可以有效提高充电站的使用效率。

（2）创新性地将充电站的选址定容对象设定为电网投资的充电站，这种充电站的建设无需考虑建设成本，而需要重点考虑可提供的社会效益。本文研究将为电网建设充电站的位置提供一定的参考。

（3）创新性地将储能容量纳入了充电站的选址定容研究中，所产生的储能容量可以有效降低实际储能建设成本，具有一定的社会效益，对电网也有积极影响。