带电粒子在匀强电场中的动能最值问题分析

■华中科技大学附属中学 许 文

带电粒子在匀强电场中受到恒定的静电力作用，在不同的初速度的情况下，粒子可能做直线运动，也可能做类抛体曲线运动。在一定区域内，若粒子运动到某处时的动能最大(最小)，根据动能定理可知，粒子从开始运动到此处合力做的功最大(最小)。下面通过典型实例分析带电粒子在匀强电场中圆周上的动能最值问题，供同学们参考。

一、问题推论

如图1 所示，匀强电场中有一个圆周，电场方向平行于圆周平面。从圆周上某点A在圆周平面内沿各个方向发射初动能相同的带电粒子，其中过圆周上B点时粒子的动能最大。可以得出以下推论:

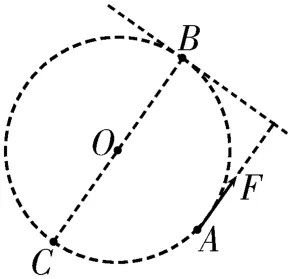
图1

推论1:过B点作圆周的切线，过A点作此切线的垂线，则粒子受到恒定合力F的方向与此垂线平行。

推论2:过B点作圆的直径与圆交于C点，则粒子经过圆周上C点时的动能最小。

推论3:若粒子受到的合力等于静电力，则过B、C点圆的切线即为匀强电场的等势线。粒子在圆周上B点时的电势能最小，在圆周上C点时的电势能最大。

二、实例分析

根据粒子经过圆周上动能最值点的圆的切线方向可判断粒子受到的合力方向。若粒子受到的合力等于静电力，则根据静电力的方向与粒子的电性可判断匀强电场的方向;根据电场方向可判断圆周上各点电势的分布情况。

1.粒子受到的合力等于静电力。

例1如图2所示，在光滑绝缘水平面上有一半径为R的圆，AB是它的一条直径，空间存在匀强电场，场强大小为E，方向与水平面平行。在圆周上A点有一发射器，以相同的初动能平行于水平面沿不同方向不断发射很多带电荷量均为+q的小球，不考虑小球间的相互作用，这些带电小球会经过圆周上不同的点，在这些点中，经过C点的小球动能最大，且∠α=30°，下列说法中正确的是( )。

图2

A.电场的方向垂直于直径AB斜向上

B.电场的方向垂直于直径AB斜向下

C.小球在A点垂直于电场方向发射，若能经过C点，则其初动能为

D.小球在A点垂直于电场方向发射，若能经过C点，则其初动能为

解析:带电小球在光滑绝缘的水平面上运动，受到的合力等于静电力。小球以相同的初动能从A点开始运动，经过C点时动能最大，说明小球在圆周上C点时的电势能最小;因为小球带正电，所以圆周上C点为电势最低处，电场线方向沿过C点的直径方向且指向C点，选项A、B错误。如果小球在A点垂直于电场方向发射，则小球做类平抛运动，经过时间t到达C点时有，解得，选项C 正确，D错误。

答案:C

点评：本题中带电小球在与电场方向平行的光滑绝缘水平面上运动，小球受到的合力等于静电力。只有静电力做功时，小球的动能与电势能之和为一定值。当小球的动能Ek最大（最小）时，电势能Ep最小（最大）。

例2如图3所示，匀强电场与圆心为O、半径为R的圆面平行，∠aOb=60°。在圆周上a点有一粒子源，能以相同的速率向圆面内各个方向发射质量为m、带电荷量为+q的粒子，粒子的初动能为Ek。有些粒子会经过圆周上不同的点。已知粒子经过圆周上b点时的动能为3Ek，粒子经过圆周时的最大动能为4Ek。不计粒子重力及粒子间的相互作用，下列说法中可能正确的是( )。

图3

C.电场方向从a点指向b点

D.粒子在圆周上a点时的动能最小

解析:设匀强电场方向与ab连线成θ角，过O点作一条与电场方向平行的直线与圆交于c、d两点，如图4所示，则粒子经过圆周上d点时的动能最大。粒子从a点运动到b点的过程中，根据动能定理得qERcosθ=3Ek-Ek;粒子从a点运动到d点的过程中，根据动能定理得。联立以上二式解得sinθ=0 或。当sinθ=0，即θ=0°时，电场方向从a点指向b点，电场强度大小，选项A、C正确;当时，电场强度大小，选项B 正确;无论sinθ=0 或，a点均不是圆周上电势最高的点，粒子在圆周上a点时的动能不是最小值，选项D 错误。

图4

答案:ABC

点评：本题给出粒子的初动能及粒子到达圆周上另两点的动能，根据动能定理可求出粒子从初始位置分别运动到圆周上这两点过程中静电力做的功；结合几何知识可判断静电力的方向，根据粒子的电性可判断电场的方向，根据电场方向可判断圆周上电势的最值点，进而可判断粒子在圆周上电势能与动能的最值点。

2.粒子受到的合力等于静电力与重力的矢量和。

例3如图5所示，AB、CD分别为竖直平面内圆的水平与竖直直径，范围足够大的匀强电场与该圆面平行，电场强度，将质量为m、带电荷量为+q的小球(可视为质点)从D点分别以相同的速率沿圆面向各个方向抛出，已知小球经过圆周上B点时的动能最大。不计空气阻力，重力加速度为g，则下列说法中正确的是( )。

图5

A.电场的方向从A点指向B点

B.小球运动过程中的加速度大小为g

C.圆周上B点的电势最低

D.小球经过C点时的速度与其初速度大小相等

解析:小球受到的静电力大小F=qE=2mg。小球从D点运动到B点的过程中合力做功最大，可知小球受到的合力F合的方向与过B点圆的切线垂直，即F合的方向水平向右。如图6 所示，根据矢量的合成法则可知，小球受到的静电力F的方向与水平方向间的夹角θ满足，即θ=30°;小球带正电，可知电场方向与直径AB成30°角斜向右上方，选项A 错误。小球受到的合力大小，小球的加速度大小，选项B 错误。作过圆心的电场线交B、C两点间的圆周于P点，P点是圆周上电势最低的点，选项C 错误。小球从D点运动到C点合力做功为零，动能不变，则小球经过C点时的速度大小与其初速度大小相等，选项D 正确。

图6

答案:D

点评：本题中带电小球在与电场方向平行的竖直平面内运动，小球受到的合力等于重力与静电力的矢量和（恒定）。小球经过圆周上B点时的动能最大，说明合力做的功最大，从而可判断出合力的方向，根据矢量合成法则可判断出静电力的方向，结合带电小球的电性可判断出电场的方向，根据电场方向可判断圆周上各点电势的高低情况。

例4如图7所示，在与匀强电场方向平行的竖直平面内有一半径为R的圆，圆心为O，AD、CF分别为圆的水平与竖直直径。在圆周上B点有一粒子源，能沿圆面向各个方向射出初速率均为v0，质量为m的同种带电微粒，已知从D点离开圆周的微粒具有最大的机械能，从E点离开圆周的微粒具有最大的动能。∠AOB=∠EOF=30°，重力加速度为g，取过F点的水平面为重力势能的零势能面，不计空气阻力及微粒间的相互作用，下列说法中正确的是( )。

图7

A.电场的方向一定沿OD方向

B.通过E点的微粒的动能为

C.微粒在圆周上动能最小的点在B、C两点之间

D.微粒通过圆周上A点时的动能一定小于

解析:微粒通过圆周上D点时的机械能最大，说明微粒从B点运动到D点的过程中静电力做功最多，因此过D点圆的切线为等势线，微粒在D点受到的静电力沿OD方向，但不知微粒的电性，故不能确定电场的方向，选项A 错误。微粒通过圆周上E点时的动能最大，说明微粒从B点运动到E点的过程中合力做功最多，因此微粒受到的重力与静电力的合力沿OE方向，根据矢量合成法则得，根据能量守恒定律得，解得，选项B 正确。延长EO与圆交于B、C两点间某点，微粒通过此点时合力做的负功最多，微粒的动能最小，选项C正确。微粒从B点运动到A点的过程中合力做正功，故微粒通过A点时的动能一定大于，选项D 错误。

答案:BC

点评：机械能的增量等于除重力之外其他力做的功，本题中除重力之外的其他力就是静电力。根据微粒经过圆周上D点时的机械能最大可知，微粒从B点运动到D点的过程中静电力做功最多，过D点圆的切线为匀强电场中的一条等势线，进而判断出微粒受到的静电力方向；根据微粒经过圆周上E点时的动能最大可知，微粒受到的合力方向与过E点圆的切线垂直。

总之，带电粒子在匀强电场中做直线运动或类抛体曲线运动，根据粒子经过圆周上某点的动能或机械能或电势能取最值，可判断静电力或合力与圆周上该点的切线垂直，再充分利用圆周的几何性质，并结合功能关系、力与运动的关系、矢量的合成法则、电场线与电势的关系、匀强电场的场强与电势差的关系等，即可顺利完成对相关问题的分析与判断。

跟踪训练

1.如图8所示，圆心为O，半径为R的圆形光滑绝缘水平轨道处在与轨道平面平行的匀强电场中，已知A、O两点间的电势差U＞0。一带正电的小球套在轨道上沿轨道运动，小球经过A、B两点时的速率均为v0，∠AOB= 120°。下列说法中正确的是( )。

图8

A.小球从A点到B点做匀速圆周运动

B.小球从A点运动到B点的过程中，动能先增大后减小

D.圆周上电势最高的点与O点的电势差为2U

2.如图9所示，在竖直平面内存在水平向右的匀强电场，电场强度E=1×104N/C。在匀强电场中有一根长l=2 m 的绝缘细线，一端固定在O点，另一端系一质量m=0.08 kg的带电小球，小球静止时悬线与竖直方向成α=37°角。若小球获得一定初速度后恰能绕O点在竖直平面内做圆周运动，取小球静止时的位置为零电势能点和零重力势能点，重力加速度g=10 m/s2，sin 37°=0.6。下列说法中正确的是( )。

图9

A.小球的电荷量q=6×10-5C

B.小球经过c点时的动能最小，且为1 J

C.小球经过b点时的机械能最小

D.小球在运动过程中的电势能和机械能之和保持不变，且为5 J

参考答案:1.CD 2.AD