考虑决策惯性的多元路径选择模型

张丽娟 李江林 肖海承

摘 要：为研究决策惯性在出行者路径选择行为中的影响，将出行者分为高敏感型和低敏感型。在决策惯性影响与超出决策惯性影响的基础上，分析出行者在路径选择中的实际行为。从真实的决策结果出发，明确了惯性决策临界值的计算方法，通过量化对决策惯性的影响范围进行描述；分析了不同情境下的惯性行为及影响因素，采用因果图和贝叶斯网络寻求变量间关系；构建不同情境下的多元路径选择模型，从而因地制宜地计算路径选择概率。通过验证数据集，对构建模型进行验证。研究结果表明，决策惯性在出行行为中真实存在，对不同情境下的路径选择概率有不同影响，在考虑路径选择时考虑决策惯性将得到更精准的结果；同时，惯性临界值对模型的选取有较大的影响。

关键词：综合交通运输；路径选择模型；贝叶斯网络；参考依赖理论

中图分类号：F511.3文献标识码：A文章编号：1005-6432（2024）03-0193-06

DOI：10.13939/j.cnki.zgsc.2024.03.046

1 引言

出行者是交通行为的主体，其路径决策行为影响城市交通流的分布情况，进而对城市建设和管理产生影响。传统的路径选择模型以出行者完全理性为前提，以效用最大为目标，寻求全局最优路径分配方法。但决策惯性、个人偏好、有限理性的存在使传统方法的目标难以实现[1]。

惯性的概念最早出现在物理学中，它是指物体保持原有状态不发生变化的一种性质。行为学中，将出行者具有保持原有选择不变的性质称为决策惯性。研究表明，在惯性作用下，除非替代方案的效用足够高，否则人们倾向于选择习惯的方案[2]。Chorus[3]也指出，由于信息不可靠、信息成本昂贵及出行者的有限理性，惯性不会被轻易破坏。因此，在路径选择中考虑决策惯性是有必要的。

研究者从不同角度对决策惯性进行讨论。刘凯等[4]探讨信息有无情况下，出行者在考虑惯性、交通信息、出行时间三方面的路径决策模型。宗芳等[5]分析了習惯和实时路况对路径选择的影响，结果表明习惯对出行者路径选择的影响程度更大。徐红利等[6]提出一种可变的价值系数描述出行者的决策惯性，定义了随机网络中决策惯性的数学表达，研究发现构建的模型具有一般性。赖元文等[7]以参考依赖理论为框架，在高时间价值与低时间价值人群中进行分析，结果表明建立的选择模型在不同情况下都能很好地描述出行者的选择行为。Junlin Zhang等[8]提出了运输网络中路线选择标准下惯性的精确定义，建立惯性模式下交通流分配问题的变分不等式，同时分析了交通信息对缓解惯性的影响。Karthik K Srinivasan等[9]考察实时信息下出行者依从性和惯性两种机制，提出框架模拟路径选择的情况，结果表明路线选择行为中依从性和惯性同时存在，并研究了相关影响因素。Alós-Ferrer Carlos等[10]利用两个研究，说明了惯性决策的真实存在性，同时还发现决策惯性的倾向与一致性偏好呈正相关。Cherchi等[11]使用RP、SP调查数据集研究惯性问题，寻找新的衡量惯性的方法，使用Logit模型解释惯性效用与调查数据集的相关性。

目前，国内外对惯性决策的研究多以理论为主，实际路网的验证和应用较少；从出行者角度出发的研究较少，对决策惯性的影响因素及作用机制未深入讨论。文章基于路径参考依赖的框架构建路径选择的多元Logit模型和贝叶斯网络，分析出行者不同属性对决策惯性的影响，讨论多情境下决策惯性路径选择的影响。

2 多元路径选择模型

2.1 多元Logit模型

多元Logit模型能够联系路径效用，计算各路径被选择的概率[7]，传统Logit模型计算路径选择概率的计算方法如下：

P（i）=prob（U（i）>U（j），i≠j）=eU（i）∑jeU（j）（1）

其中，U为效用函数。基于参考依赖理论与决策惯性，将出行者的习惯路径k作为参考点，式（1）中的效用函数则变为替代路径i相对参考点的效用增益值。

U′（i）=U（i）－U（k）（2）

基于式（2），式（1）变式为：

P（i）=prob（U′（i）>U′（j），i≠j）=e（U（i）－U（k））∑je（U（j）－U（k）） （3）

式（3）为不考虑惯性决策的情况下，传统Logit模型的表达，为方便讨论，以U代替U′（i）作为文章讨论的效用函数。当考虑惯性决策的影响，式（3）不再适用，构建贝叶斯网络获取路径的选择概率更为合适，具体方法会在后面章节中详细阐述。

2.2 出行效用函数

出行效用函数通常由成本构成，在一次出行中最多考虑的是时间成本和费用成本。在计算出行成本时，文献[12]、[13]结合时间与费用，构建广义出行成本，即：

U（T，M）=ω1ωvotT+ω2F（4）

其中，U（T，M）为效用函数，T为出行时间，ωvot为出行者时间价值参数，F为出行费。

用ω1、ω2为权重系数，且ω1+ω2=1。

2.2.1 时间价值参数

传统方法以GDP计算ωvot，ωvot为一个固定的值，这样的表达方法适应性不足。参考依赖理论，时间价值参数同样基于参考点，其值与参考路径k有关且在一定范围内波动，即ωvot∈（ω-，ω-）。因此，文章将ωivot定义为替代路径i的相对时间价值参数，计算方法如下。

ωivot=mi－mktk－ti，tk≠ti0，tk=ti（5）

记OD集合为W，可选路径集合为Rw={i1，i2，…，in，k}，ωivot的范围表示为：

mini∈Rw{ωivot}≤ωvot≤maxi∈Rw{ωivot}（6）

2.2.2 时间费用权重

效用中的时间权重ω1、费用权重ω2与出行者对成本增加的容忍阈值有关，该值与出行者属性有关，需分情况讨论。

以时间成本为基准进行分析，对于高时间敏感者而言，减少单位时间成本带来的是负效应；相反，对于低时间敏感者，减少单位费用成本是正收益。

分类讨论ω1、ω2的取值。为了便于表述，将效用U分为时间效用UT和费用效用UF。

UT=ω1ωivot（Ti－Tk）（7）

UF=ω2（Fi－Fk）（8）

情形1：对于低时间敏感度的出行者，出行成本减少带来的效用无法吸引他们，但对增加时间换取的费用减少较为敏感。此时ω1<ω2，且费用增加为负效应，时间的减少为正效应。

情形2：高时间敏感度的出行者更重视时间成本的减少，此时ω1>ω2，且时间成本的增加为负效用，费用成本的增加为正效用。

2.2.3&nbsp;换算系数

在表达出行效用时，时间成本与费用成本由于单位不同，在取值时相差较大，在计算概率时容易造成部分路径效用值过大或过小。因此，定义一个换算系数βi，表示路径i相对k的换算系数。

βi=（ti－tk）/tk（mk－mi）/mk（9）

经过处理后，出行费用成本可转换为时间成本，两者数值将比处理前平均。效用函数表示如下。

U（T，M）=ω1ωvotT+ω2βiF（10）

2.3 决策惯性

决策惯性并非能够始终对出行者产生作用，文献[14]認为，对于路径选择，若路线的成本超过某一阈值，则该路径可能会被放弃。类似的，当选择i路径带来的效益超过某值时，决策者不再受惯性牵制，将该值定义为惯性临界效用值，可以描述如下。

U（ti，mi）－U（tk，mk）≤ε（11）

当等号取得时，ε值可描述为：

ε=ω1ωivot（Ti－Tk）－ω2（Fi－Fk），UF≤0，UT>0ω2（Fi－Fk）－ω1ωivot（Ti－Tk），UF>0，UT≤0（12）

该值定义了一个范围（－ε，ε），在该区域内惯性能够作用于出行者，将该区域定义为惯性影响带。而超出该范围的值时，惯性不再产生作用。定义一个二值的分段函数G（i）描述不同范围的不同情况。

G（i）=1，-ε≤U（ti，mi）－U（tk，mk）≤ε0，其他（13）

其中，0表示超出惯性临界值，不受惯性影响；1表示受惯性影响。根据Logit模型，路径选择是否受惯性影响的概率可以表示为：

P（G=1）=P（-ε≤U（ti，mi）－U（tk，mk）≤ε）（14）

P（G=0）=1－P（G=1）（15）

在受到决策惯性影响时，出行者自身的属性也会极大程度地影响惯性概率。为更合理的构建惯性影响的路径决策模型，还需要对出行者个人特征和实际选择进行调查，获取数据以标定效用函数中的未知变量。

3 图模型

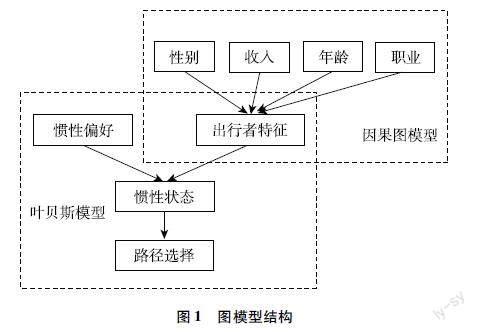
图模型能够清晰直观的表达变量之间的相关关系和因果关系，在描述出行者对惯性决策的影响时，可以构建因果图模型和有向无环的贝叶斯网络进行描述，涉及的变量和关系如图1表示。

图1 图模型结构

3.1 因果图模型

记存在两个因果变量为X和Y，在其他因素不变的情况下，X的变化引起Y的改变。Y的改变称为因果效应，衡量因果效应的大小主要通过计算ITE或ATE完成，其中ATE更适用于评估整体效果[15]。因果推断的最终目标就是寻求ATE的值。

ATE（X→Y）=E［Y|do（Xi=1）－Y|do（Xi=0）］（16）

通过do运算后，Z与X之间的联系被消除，因果图由a变为b，X与Z相互独立，而do运算后与运算前的概率也存在关系[16]：

P（Y=y∣do（X=x））=P′（Y=y∣X=x）（17）

P（Y=y∣do（X=x））=∑P（Y=y∣X=x，Z=z）P（Z=z）（18）

公式中的右项是已知的，可以通过观测到的数据进行干预。以实测数据代入推断模型，可以求得变量之间的因果关系。

3.2 贝叶斯网络

贝叶斯公式由条件概率与全概率公式的概念转化而来，记选择i路径为事件A，惯性状态为事件B，在B前提下A发生的概率可记为：

PG（Ai|B）=P（Ai）P（B|Ai）∑nj=1P（Aj）P（B|Aj）（19）

P（A|B）称A的后验概率，P（A）称A的先验概率。将某研究系统中涉及的随机变量关系绘制在一个有向图中，就形成了贝叶斯网络。借助贝叶斯网络，使用极大似然估计（MLE）可以寻求因素之间的关系。

求解未知参数即为寻找条件概率最大的解，即求使P（Z|X）最大的参数X，其目标可以表示如下。

argmaxXP（X|Z）（20）

构建似然函数L（Θ|J），其中，样本集合J=x1，x2，x3，…，xn，同时各样本间相互独立，对似然函数进行变换求解，得到目标条件概率的估计值，似然函数形式如下。

L（Θ|J）=∏ni=1P（X=xi）∏ni=1PZ=zi|X=xi（21）

4 实例分析

4.1 数据来源

以昆明市呈贡片区17个OD点对间的88条路径为例设计问卷，对居民个人信息和路径选择行为进行调查，调查基本涵盖各个年龄段。调查共计发放问卷1200份，最终回收有效问卷1031份，有效率为85.92%。 将收集到的问卷数据用于模型拟合与模型验证，其中，拟合数据集涉及10个OD点对， 47条路径，共634个数据。验证集涉及7个OD点对，33条路径，共397个数据。拟合数据集用于模型的训练以及函数中未知参数的标定，验证集用于验证模型的有效性。

问卷涉及的路径皆为有效路径，时间成本、费用成本、OD间间距的三维关系及在X、Z轴的映射。

4.2 模型构建与参数标定

4.2.1 因果图模型

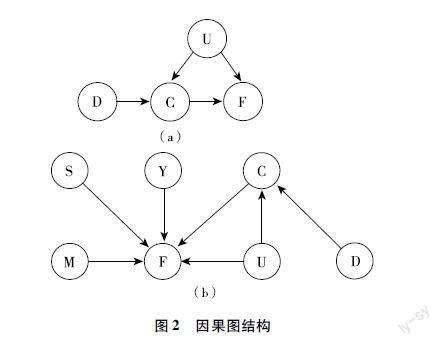
记D表示出行目的，C表示职业，S表示性别，Y表示年龄，M表示收入，F表示出行者特征，取值为0、1分别表示低时间敏感度出行者与高时间敏感度出行者，U表示无法直接观测到的变量，构建的因果图如图2所示。

图2 因果图结构

其中，C与F并没有直接的因果关系，但存在无法观测的变量U作用于C、F，引入工具变量D来表征三者之间的相互关系，如图3（a）所示。

上述结果展示了出行者特性与个人属性之间的关系。女性对时间成本的敏感度更高；高收入和低收入的出行者对时间成本敏感度更高；学生、公司或机关事业单位的出行者对时间更敏感。综合来讲，年龄对出行者敏感度几乎无影响，性别、收入的影响程度较小，职业影响程度相对最大。

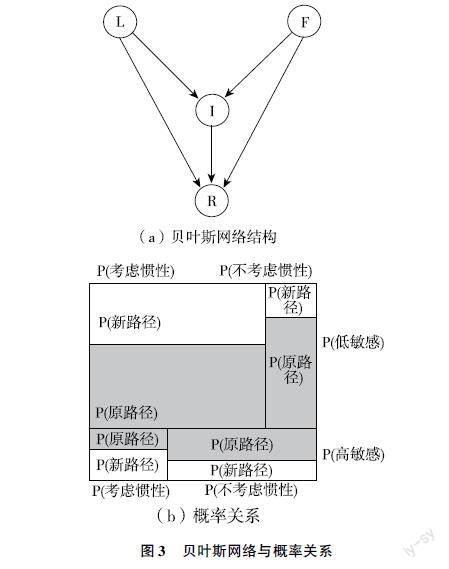
构建贝叶斯网络，寻找出行者特征、惯性偏好、惯性状态、路径选择之间的数量关系。其中，L代表惯性偏好，I代表惯性状态，R代表选择路径，见图3。

根据极大似然估计的原理以及已知的先验概率，对各节点的后验概率进行估计求解，进行横向对比作图4（a） ～（d）。

图3 贝叶斯网络与概率关系

图4 概率横向对比

由图4（a）～ （b）可知，考虑惯性时，低时间敏感度人群受到惯性的影响大于高时间敏感度人群；不考虑惯性作用时，低时间敏感度的人群受到惯性影响依然大于高时间敏感度人群。这说明，决策惯性对高时间敏感度人群效用更小，对低时间敏感度人群效用更大。由图4（c）可知，通常存在惯性偏好的出行者更有可能在最终决策中存在惯性，而不存在惯性偏好的出行者在实际情况下也有可能表现出惯性。这其实是一种有限理性的体现，出行者的计划与实际情况下的选择可能不一致。无论是否在路径选择中存在惯性，最终选择习惯路径的概率都会大于选择新路径的概率，在存在惯性时这一现象更加明显。由图4（d）可知，惯性的确影响着出行者的路径选择，考虑惯性影响的路径选择情况与实际更为符合，且与实际的误差比不考虑决策惯性降低了30.17%。

4.2.2 模型参数标定

利用贝叶斯网络求得的各节点概率分布（CPD），可以对路径选择模型中的未知参数ω1、ω2进行标定。P（R|I，F）用于标定不同情况下路径选择模型中的ω1、ω2，结果表明决策惯性对低敏感人群的影响并不显著。

而对于惯性临界效益ε，构建一个最优化问题进行求解，其目标函数如下所示。

minSSE=∑ni=1（P（i）－P^（i））2（22）

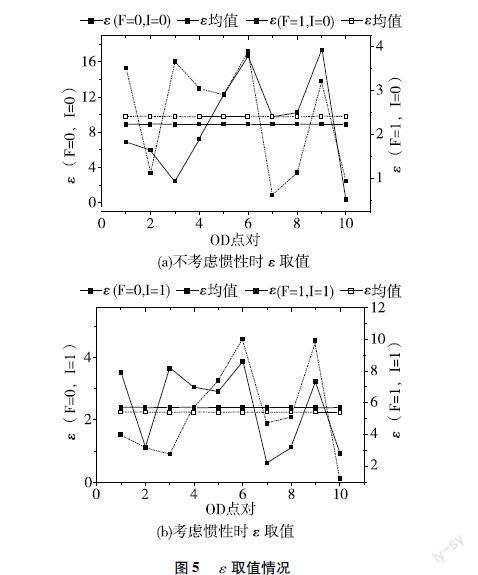
其中，各参数的表达见式（16）～（19）。求解得到在高时间敏感度和低时间敏感度两种情况下，考虑决策惯性的10个OD点对的ε取值情况，对10个值做算术平均，得到通用的临界值，如图5所示。在惯性区间带（－ε，ε）中，决策惯性对出行者最终决策行为的影响是显著的。

图5  ε取值情况

4.3 模型验证

利用前述章節拟合的模型及标定的参数，在验证集中进行验证。以7个OD点对共33条路径的397份问卷数据为基础，验证前述模型的有效性。此处仅研究最终选择为原路径的概率情况，选择其他路径的情形不在文章研究范围内。

4.3.1 惯性影响范围内

情形1：对于高时间敏感度人群，考虑决策惯性时选择原路径的概率为0.361，与真实值的误差为0.0453；不考虑决策惯性时选择原路径的概率为0.155，与真实值的误差为0.1756。

情形2：对于低时间敏感度人群，考虑决策惯性时选择原路径的概率为0.835，与真实值的误差为0.0681；不考虑决策惯性时选择原路径的概率为0.214，与真实值的误差为0.1296。

模型计算出最终选择原路径的理论概率值与实际概率对比，真实值与理论值的误差如表1所示。

从上述图表可以观察到，考虑决策惯性影响的人群路径选择概率与实际情况更加接近。通常MAPE小于10时，预测精度较高，表1中MAPE均远小于10，说明使用文章模型估计选择概率是合理的，且考虑惯性时的理论值比不考虑惯性的理论值效果更佳。而表中MAE与MSE值均小于1，与实际情况越接近，且考虑惯性时比不考虑惯性的计算误差更小。研究证明出行者在决策行为中的确存在惯性，且与文章提出的模型拟合良好。

4.3.2 惯性影响范围外

情形1：对于高时间敏感度人群，选择原路径的真实概率为0.056。多元路径选择函数下选择原路径的概率为0.019，与真实值的误差为0.0014；贝叶斯模型下选择原路径的概率为0.155，与真实值的误差为0.0097。

情形2：对于低时间敏感度人群，选择原路径的真实概率为0.102。多元路径选择函数下选择原路径的概率为0.085，与真实值的误差为0.00025；贝叶斯决策下选择原路径的概率为0.214，与真实值的误差为0.0126。

两种计算方式的理论值与真实值对比如图6所示。低时间敏感度时，Logit模型计算值与真实值之间的误差比贝叶斯网络低97.95%；高时间敏感度时，Logit模型的误差比贝叶斯网络低85.5%。可以得出结论，无论是高时间敏感度人群还是低时间敏感度人群，Logit模型计算路径的选择概率与现实情况更接近，平均误差小92.55%。

图6 Logit与贝叶斯计算结果对比

5 结论

文章研究了随机OD点对中，决策惯性对出行者路径选择行为的影响。通过构建基于参考依赖理论的多元路径选择模型，定义相对效用函数和惯性影响临界值。通过因果图模型，分析了惯性的影响因素。通过贝叶斯网络模型，分析了不同时间敏感度出行者在惯性影响下的选择行为，并用反推了惯性临界值和模型参数。采用实例数据验证了所构建模型的有效性，研究得到的结论如下三点。

（1）对某随机网络中出行者路径选择行为进行研究时，需要考虑是否处于惯性决策的影响范围内，对范围内的出行行为与范围外的出行行为需分类讨论。

（2）文章提出的采用因果图和贝叶斯网络计算变量间关系的方法是可行的，在考虑决策惯性影响的前提下，该模型与真实情况较吻合，是一种有效准确的模型，且具有一定的移植性，可用于衡量惯性条件下路径选择概率。

（3）多元Logit模型用于描述超过惯性影响范围的路径选择行为是合理的，经过验证以该方法计算的路径选择概率与真实情况较吻合，使用图模型反推的参数是合理有效的。

参考文献：

[1] PATRIKSSON M. The traffic assignment problem：models and methods[M].Mew York：Povers Publiconer，2015.

[2] TRAIN E. Discrete choice methods with simulation[M].Cambridge： Cambridge University Press， 2009（2）.

[3] CHORUS C， DELLAERT B G C. Travel choice inertia：the joint role of risk aversion and learning[R].Rochester， NY： Social Science Research Network， 2010.

[4] 刘凯， 周晶， 徐紅利， 等. 交通信息对出行者路径选择惯性行为的影响[J].系统管理学报， 2018， 27（6）： 1065-1073.

[5] 宗芳， 路峰瑞， 唐明， 等. 习惯和路况对小汽车出行路径选择的影响[J].吉林大学学报（工学版）， 2018， 48（4）： 1023-1028.

[6] 徐红利， 刘煜昊， 徐薇， 等. 考虑决策惯性的随机网络路径选择与交通流分配模型[J].系统工程理论与实践， 2021， 41（4）： 1010-1017.

[7] 赖元文， 胡亮， 林力. 基于参考依赖理论的出行者路径选择模型研究[J].公路交通科技， 2021， 38（7）： 131-137.

[8] ZHANG J， YANG H. Modeling route choice inertia in network equilibrium with heterogeneous prevailing choice sets[J].Transportation research part C： emerging technologies， 2015（57）： 42-54.

[9] SRINIVASAN K K， MAHMASSANI H S. Modeling inertia and compliance mechanisms in route choice behavior under real-tme information[J].Transportation research record： journal of the transportation research board， 2000， 1725（1）： 45-53.

[10] ALS-FERRER C， HGELSCHFER S， LI J. Inertia and decision making[J].Frontiers in psychology， 2016（7）.

[11] CHERCHI E， MANCA F. Accounting for inertia in modal choices： some new evidence using a RP/SP dataset[J].Transportation， 2011， 38（4）： 679-695.

[12] 高婷婷， 王武宏. 基于時间价值的城市交通出行成本研究[J].铁道运输与经济， 2014， 36（2）.

[13] 张凌煊， MENENDEZ M， 张士行， 等. 考虑街区尺寸的不同交通方式广义出行成本分析[J].交通运输系统工程与信息， 2019， 19（2）： 166-174.

[14] CARRION C， LEVINSON D. Route choice dynamics after a link restoration[J].Transportmetrica B： transport dynamics， 2019， 7（1）： 1155-1174.

[15] ZHANG&nbsp;A， GAO J， LI Y， et al. A survey on causal inference[J].ACM transactions on knowledge discovery from data （TKDD）， 2021.

[16] TSODIKOV A. Causal inference in statistics： a primer， Judea Pearl， Madelyn Glymour and Nicholas P[J].International statistical review， 2020， 88（1）： 256-258.