基于HME-ABC 算法的多无人直升机时间协同航路规划
韩增亮 陈 谋 朱豪杰 吴庆宪
在军事领域,UAH 凭借其能够在复杂危险环境工作的出色能力,成为近年来最具发展前景和挑战的军事装备之一[1].随着现代空战技术的不断发展,军事侦察与打击任务的复杂性日益增加,单机侦察与打击模式已无法满足当前的军事任务需求,多机协同作战成为UAH 在战场作战的主要形式.航路规划作为UAH 协同作战的基础,能够为每架UAH 提供一条安全无碰撞的最优飞行航路,使UAH 编队能够安全有效地完成预定任务[2].因此,高效合理的协同规划技术便成为了任务能否成功的关键.
学者们提出了一系列方法来处理UAH 的航路规划问题,例如人工势场(artificial potential field,APF)算法、A* 算法、Voronoi 图算法以及快速探索随机树(rapidly-exploring random tree,RRT)算法等[3-6].上述优化算法在处理具有复杂约束的航路规划问题时,普遍存在搜索时间长、易陷入局部最优等问题.随着计算智能的提出与发展,群智能算法逐渐成为解决航路规划问题的热门方向.文献[7]提出了一种具有贪婪启发机制的遗传算法,通过对风速与风向的评估规划无人机三维紧急降落航路规划问题;文献[8]提出了一种基于量子粒子群优化的混合差分进化(quantum-particle swarm optimization,Q-PSO)算法,利用不同算法的融合为海上UAV 提供了飞行航路方案;文献[9]提出了一种改进的离散粒子群优化(discrete-particle swarm optimization,DPSO)算法,通过采用确定性初始化、随机突变和边缘交换等方式来求解耦合旅行商问题.伴随着空战环境日益复杂,一系列新型群智能优化算法被提出并应用于航路规划问题,例如人工蜂群(artificial bee colony,ABC)算法、狼群搜索(wolf pack search,WPS)算法、混合蛙跳(shuffled frog leaping,SFL)算法和杜鹃搜索(cuckoo search,CS)算法等[10-13].同时,随着群智能算法的深入研究与发展,其改进型算法成为了协同航路规划问题的热门研究方向,见文献[14-18].通过大量的文献分析可以看出,无论单UAV 还是多UAV 很多研究都仅限于空间上的航路规划,这些方法更多地注重于航路避碰,却忽略了对于时间协同的考虑.然而对于多机联合作战任务,往往需要多架UAV 能够在规定时间约束下从不同的起点同时飞至指定的任务区域,使其能在有效时间窗口下协同执行侦察或打击任务.这就需要UAV 编队的飞行航路要满足时间协同性的要求.因此,时间上的协同便成为了UAV 联合作战任务成功关键因素,所以为UAH 编队规划出带有时间协同约束的飞行航路就显得极其重要.
本文针对多UAH 时间协同航路规划问题,研究了一种基于异维记忆进化策略的人工蜂群协同航路算法,利用蜂群的记忆模式与信息交互能力设计了异维记忆知识库用来取代传统ABC 算法单一随机的搜索方式,有效地降低了蜂群的无效搜索,在减少优化迭代次数的同时显著提高了协同航路的优化效率.
1 航路规划问题建模
1.1 问题描述
多UAH 时间协同航路规划要求每架UAH 根据任务需求,从不同起点出发并同时到达目标区域执行任务.UAH 编队在飞行过程中可能面临着地形与防空武器的威胁,规划的航路须避开上述威胁区域并满足UAH 的机动性能约束.
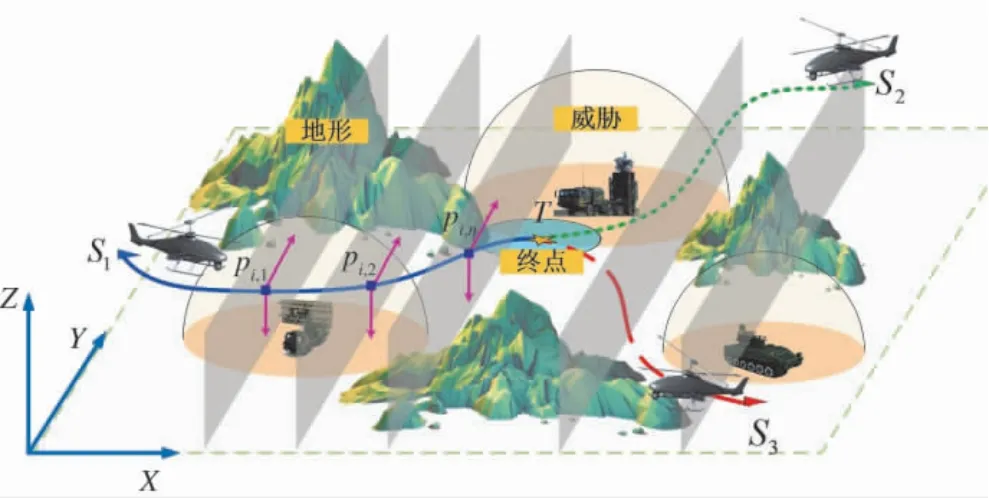
图1 多UAH 协同航路规划问题模型Fig.1 Model of multi-UAH coordinated flight path planning problem
由于对规划空间进行了垂直分割操作,航路点的寻找范围从整个三维规划空间可以缩小为N-1 个二维平面.对于每个二维平面,航路点的表征方式可以转换为.因此,多UAH 时间协同航路规划问题的优化变量E 可以被定义为:
所有航路点应满足地图边界的约束,即[8]
1.2 航路代价分析
1.2.1 油耗代价
更短的飞行航路意味着更少的燃油消耗、更短的飞行时间和更安全的飞行包线.因此,油耗代价Jl可以描述为[18]:
其中,k=1,2,…,N,N 为航路点数量,v 为UAH 的飞行速度,lk为第k 条子航迹长度,ρ 为UAH 平均油耗.
1.2.2 威胁代价
如图2 所示,将威胁区域简化为半径为R 的半球体,航路威胁代价Jt可以描述为[19]:
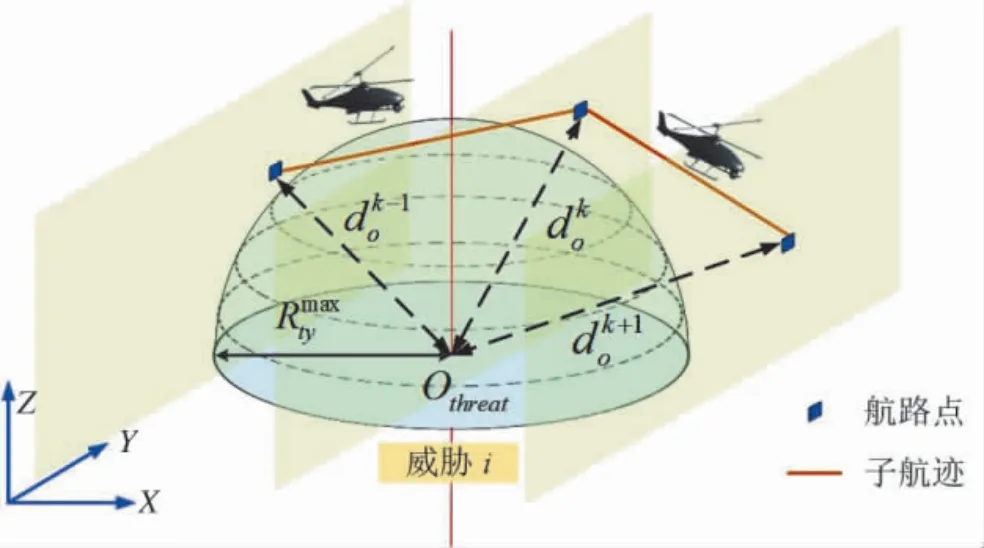
图2 威胁代价计算示意图Fig.2 Schematic diagram of threat cost calculation
1.2.3 高度代价
在保证UAH 安全飞行的前提下,降低其飞行高度可以提高UAH 的隐蔽性,如图3 所示.因此,航路的高度代价Ja可以描述为[19]:
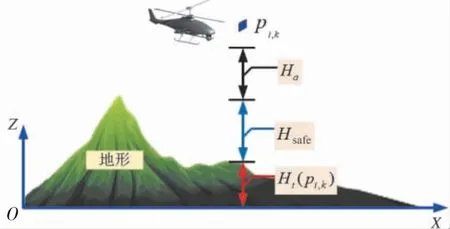
图3 高度代价计算示意图Fig.3 Schematic diagram of altitude cost calculation
1.3 航路约束分析
1.3.1 UAH 性能约束
UAH 的性能约束主要为偏航角约束与俯仰角约束,性能约束项可以表示为:
1.3.2 航路安全约束
航路安全性主要体现在UAH 与地形是否发生碰撞和UAH 之间是否发生碰撞.因此,航路安全约束可以表示为:
协同航路规划还需考虑不同的UAH 之间的航路避碰问题.首先考虑航路i 上的航路点m 与航路j上的航路点n 之间的距离是否小于预设安全距离.
1.3.3 航路协同能力
多UAH 协同航路规划的时间协同性要求每架UAH 应具有相同的编队预计到达时间(estimate time arrival,ETA).如图4 所示,UAH 编队中每架UAH 的速度范围为,则第i 架UAH 的飞行时间段为:

图4 时间协同窗口示意图Fig.4 Schematic diagram of the time synergy window
当第i 架UAH 和第j 架UAH 存在时间协同的可能性,则这两架UAH 沿航路飞行的时间应满足以下关系:
若两架UAH 飞行时间段的相交区间与两时间段中较小时间段长度之比不小于,则
2 多UAH 时间协同航路规划算法
2.1 多UAH 时间协同航路规划框架
多UAH 时间协同航路规划要求UAH 编队从不同起点出发,并在合理的时间窗口内飞至任务区域.图5 为多UAH 时间协同航路规划框架,该框架将多UAH 航路规划被转化为单UAH 航路规划,通过时间约束调整各架UAH 飞行速度,计算时间协同变量ETA,从而为UAH 编队规划出满足时间窗口的飞行路径.
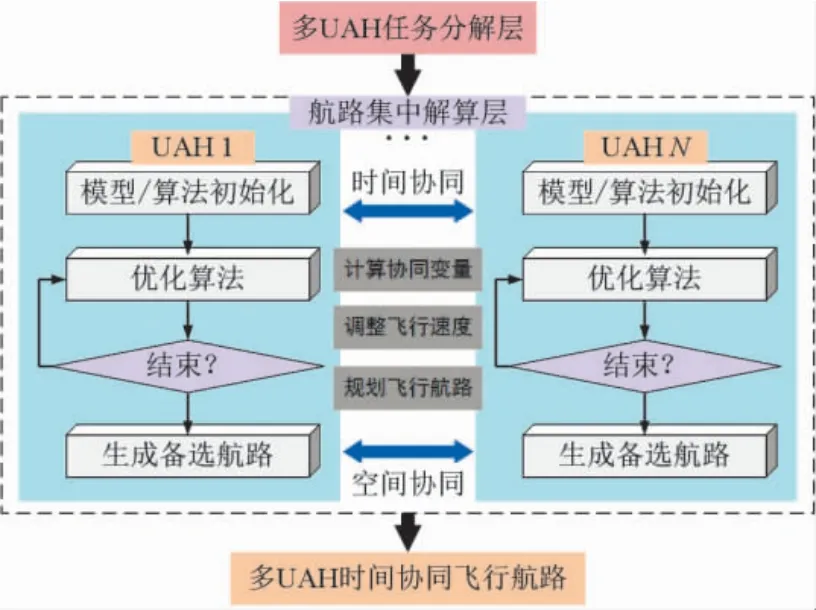
图5 时间协同航路规划框架Fig.5 Framework of time-coordinated flight path planning
2.2 基于HME-ABC 算法的多UAH 时间协同航路规划
为了提高多UAH 时间协同航路规划问题的结算效率与规划质量,本文根据蜂群的联想记忆能力提出了一种基于HME-ABC 算法.通过异维记忆知识库的引导进化降低了蜂群的无效搜索过程,提高ABC算法的收敛速度和优化效率,为UAH 编队快速高效地规划出时间协同飞行航路.详细的基于HME-ABC算法的多UAH 时间协同航路规划过程如下所示.
2.2.1 建立协同航路规划目标函数
根据战场环境配置与协同任务需求构建协同航路规划问题模型.考虑到协同航路的综合代价与约束,多UAH 时间协同航路规划目标函数可以描述为:
2.2.2 算法初始化
每个蜜源位置代表一个UAH 的候选航路点,设置雇佣蜂和观察蜂数量为SN,采用D 维向量来描述第i 个蜜源的位置信息,通过式(26)在规划空间中初始化蜜源位置[19].
2.2.3 HME-ABC 算法优化过程
1)雇佣蜂阶段
a)基于种群信息引导的平衡进化方式
该进化方式利用了种群中不同质量个体的综合信息,个体在决定更新行为时充分考虑了自身、当前最优个体和其他个体的影响.基于种群信息引导的平衡进化方式如下:
其中,fit(xi)为当前个体的适应度函数.个体适应度值计算方式如下[14]:
其中,obj(x)为备选解x 的目标函数值.
b)基于异维记忆机制的进化方式
考虑到蜂群进化存在失败概率的问题,本节为进化失败的雇佣蜂设计了一种基于异维记忆机制的进化方式,利用蜜蜂的记忆能力将进化成功经验应用于UAH 航路点的搜索.

图6 记忆知识库Fig.6 Memory knowledgebase
针对于进化失败的个体,将给予其二次进化的机会.为提高航路规划的成功率,二次进化阶段将借鉴记忆知识库中的成功案例对其进行指导.
如图7 所示,二次进化所需的信息将不再从种群中获得,取而代之的是记忆知识库中的成功经验.考虑到算法需平衡开发与探索能力,设计了如下的进化方式:

图7 二次进化示意图Fig.7 Schematic diagram of secondary evolution
HME-ABC 算法的雇佣蜂阶段流程如下.

2)观察蜂阶段
观察蜂通过雇佣蜂所分享的信息,根据蜜源质量采用轮盘赌策略选择合适的蜜源进行开采.跟随概率Pi(x)可表示为[19]:
其中,fiti(x)为第i 个蜜源的适应度.
3)侦察蜂阶段
传统的ABC 算法采用初始化策略作为侦察蜂的进化方式,搜索方向的随机性可能会降低新蜜源的开发效率.为此,将根据记忆知识库的进化经验,设计一种基于跨越式搜索的侦察蜂更新策略.
如图8 所示,侦察蜂从记忆知识库中选择两例成功进化经验,其对应的蜜源位置中心作为新蜜源位置,该过程可描述为:
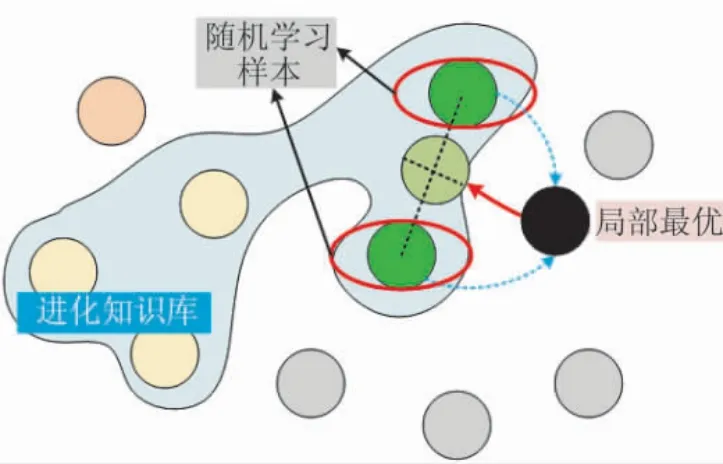
图8 侦察蜂搜索策略Fig.8 Strategy of scout bee search
2.2.4 协同航路ETA 计算
当HME-ABC 算法满足迭代终止条件,便输出最终的全局最优UAH 编队航路点序列.根据所规划出的候选航路的长度,协调各架UAH 的飞行速度,利用式(22)和式(23)计算出航路协同ETA.最终的规划结果为UAH 编队的飞行航路与协同时间窗口.
基于HME-ABC 算法的多UAH 时间协同航路规划流程如图9 所示.
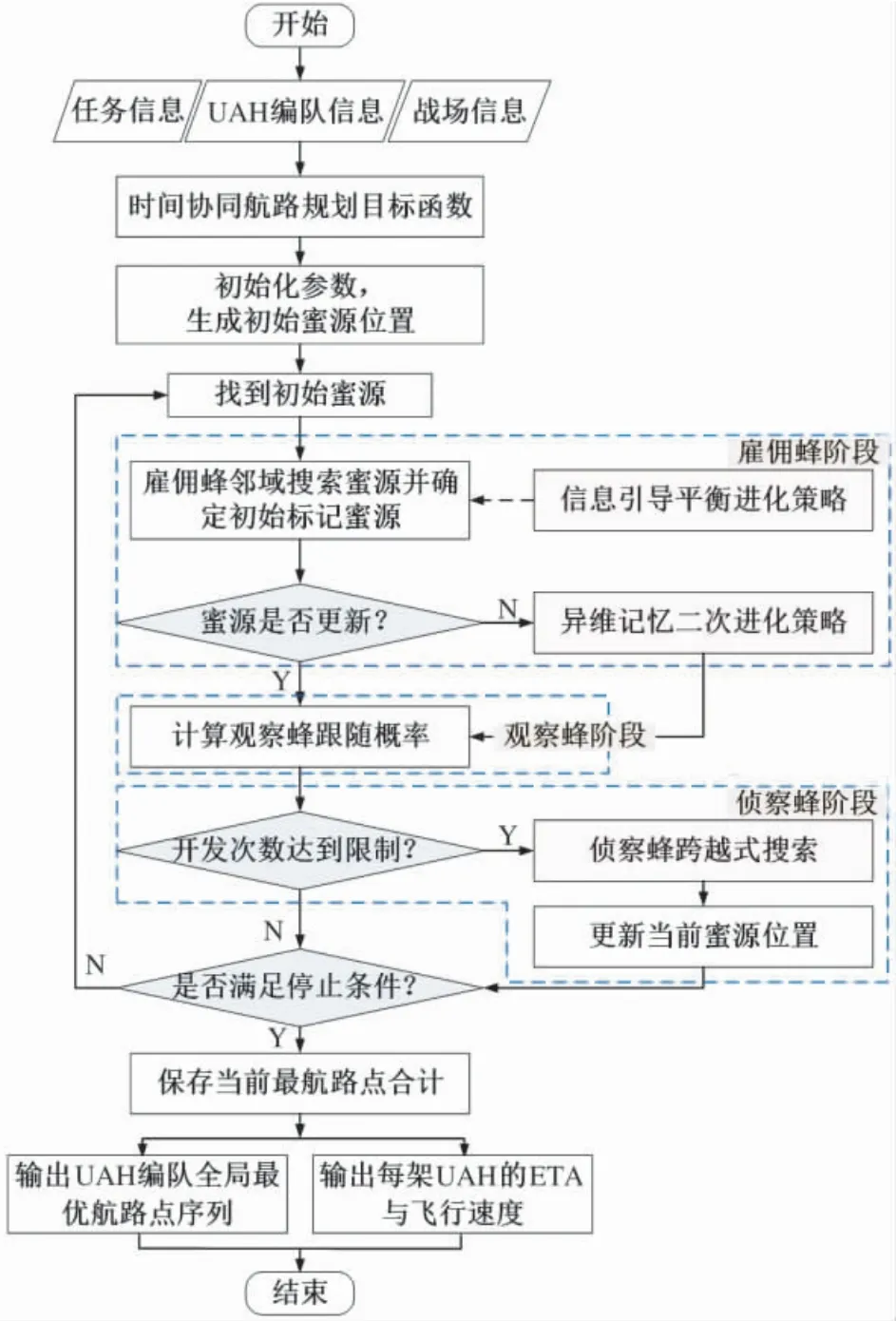
图9 HME-ABC 算法流程图Fig.9 Flow chart of HME-ABC algorithm
2.3 计算复杂度分析
HME-ABC 算法的计算复杂度由初始化阶段复杂度与优化阶段复杂度组成,具体计算如下[19].
1)初始化阶段
2)算法优化阶段
其中,O(·)表示算法渐进时间复杂度,n 代表输入数据的量.
初始化阶段只在程序开始时执行一次,优化阶段必须在每个周期中执行,直到算法结束.因此,HME-ABC 算法的最大计算复杂度可以被描述为:
相似的,传统ABC 算法的最大计算复杂度可以被计算如下:
计算结果表明,HME-ABC 算法并没有增加传统ABC 算法的计算复杂度,能够保证多UAH 时间协同航路规划系统的求解效率.并且凭借群智能算法无模型依赖的特性,HME-ABC 算法在复杂优化问题的适用性能力也能够得到保障.
3 仿真结果与分析
为验证所提模型与HME-ABC 算法在多UAH时间协同航路规划问题中的有效性,将ABC 算法、BAS-ABC 算法以及HME-ABC 算法3 种算法进行仿真实验验证[14].模拟飞行空间范围为250km× 250 km×250 km,飞行区域存在3 个不同的威胁区域,威胁信息如表1 所示.5 架UAH 分别从(171,30,30),(190,97,38),(175,185,25),(19,22,43)和(65,168,27)处起飞,任务终点位置坐标为(57,59,64).
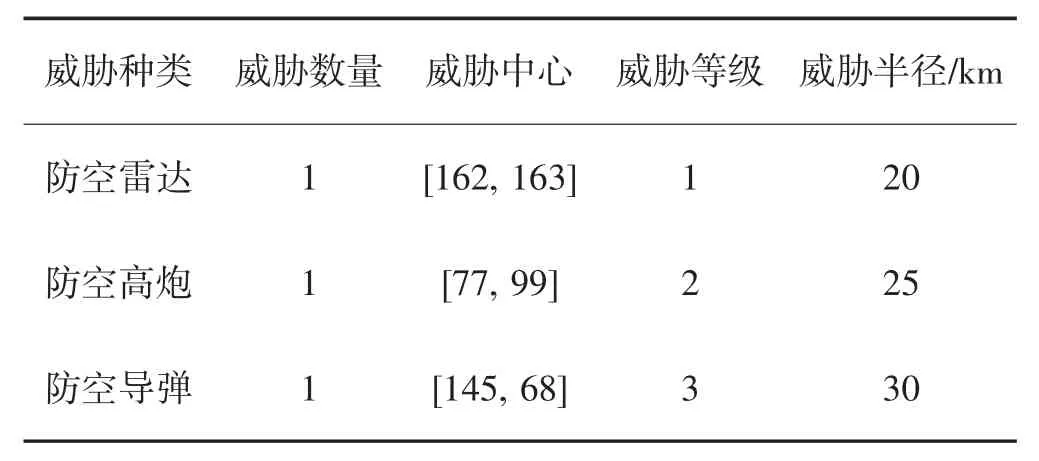
表1 仿真场景参数信息Table 1 Simulation scene parameter information
为使仿真实验的结果更加客观公平,设置3 种对比算法的种群数量SN=100,最大迭代次数Maxcycle=50,最大开采限制Limit=5,所有航迹进行平滑处理,实验结果为独立运行20 次所得.仿真结果如图10~图18 所示.

图10 基于ABC 算法的UAH 协同飞行航路Fig.10 UAH coordinated flight path based on ABC algorithm

图11 基于ABC 算法的每架UAH 航路代价值Fig.11 Cost value of each UAH flight path based on ABC

图12 基于ABC 算法的ETA 协同时间窗Fig.12 ETA synergy time window based on ABC
图10、图13、图16 为3 种算法所规划的UAH的协同飞行航路.可以直观地看出,ABC 算法所规划的飞行航路重叠区域更多,尽管UAH 在时空上并没有发生碰撞,但较多的重叠路线无形中增加了UAH编队飞行碰撞的风险.另外,BAS-ABC 算法所规划的个别飞行航路性能较差,航路长度相对较长.相比较而言,HME-ABC 算法所规划的飞行航路无论在航路质量还是UAH 飞行安全上都更加优秀.

图13 基于BAS-ABC 算法的UAH 协同飞行航路Fig.13 UAH coordinated flight path based on BAS-ABC algorithm
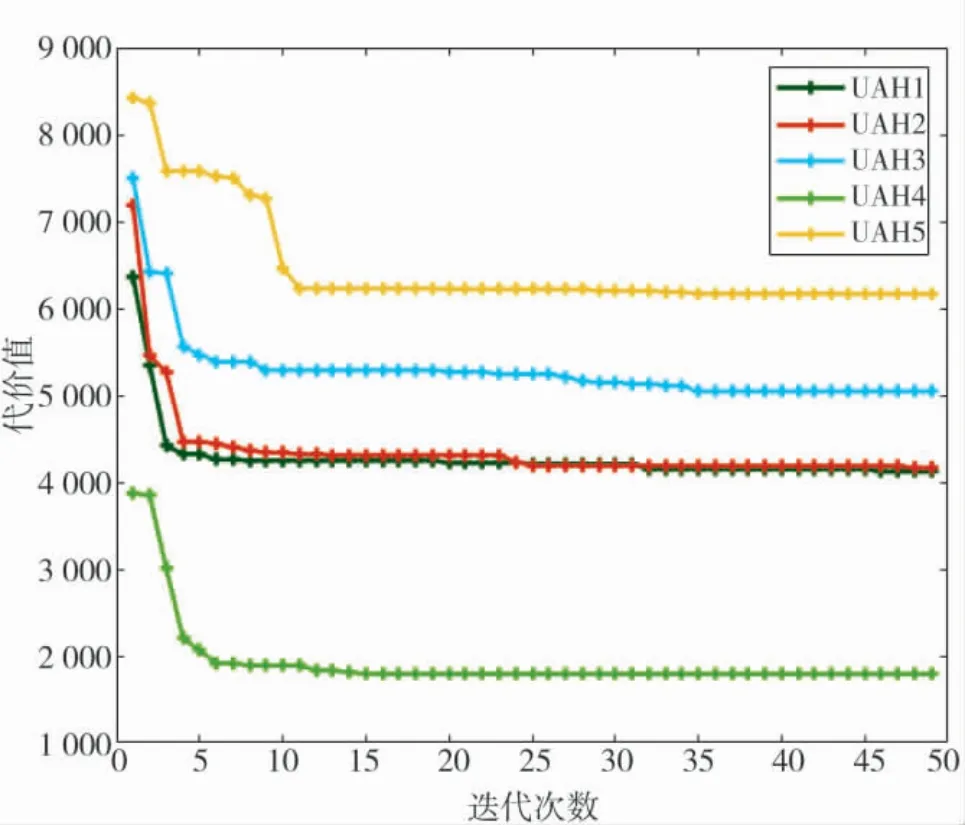
图14 基于BAS-ABC 算法的每架UAH 航路代价值Fig.14 Cost value of each UAH flight path based on BAS-ABC
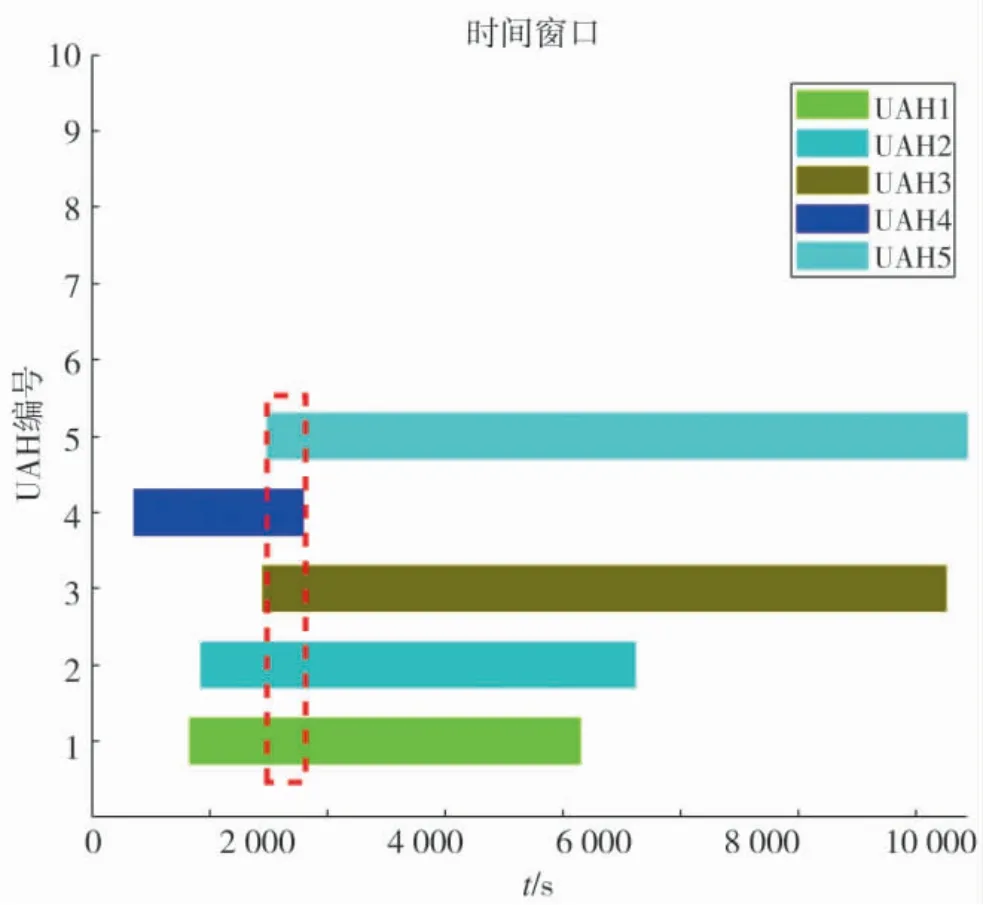
图15 基于BAS-ABC 算法的ETA 协同时间窗Fig.15 ETA synergy time window based on BAS-ABC

图16 基于HME-ABC 算法的UAH 协同飞行航路Fig.16 UAH coordinated flight path based on HME-ABC algorithm
图11、图14、图17 为3 种算法的优化迭代曲线,通过收敛曲线可以明显地看出,无论从收敛迭代次数还是最终的航路代价值,HME-ABC 的优化性能都要优于其他两种对比算法.仿真对比统计结果如表2~表4 所示,HME-ABC 算法凭借优秀的搜索策略与进化机制,能有效地避免局部最优解,使算法优化性能更加稳定且优秀.

表2 ABC 算法仿真结果统计Table 2 ABC algorithm simulation statistics results
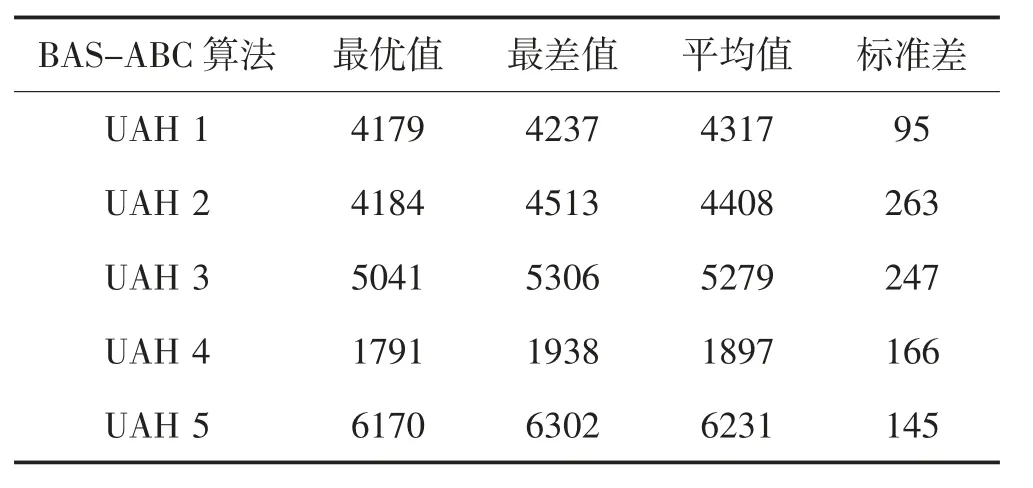
表3 BAS-ABC 算法仿真结果统计Table 3 BAS-ABC algorithm simulation statistics results

表4 HME-ABC 算法仿真结果统计Table 4 HME-ABC algorithm simulation statistics results
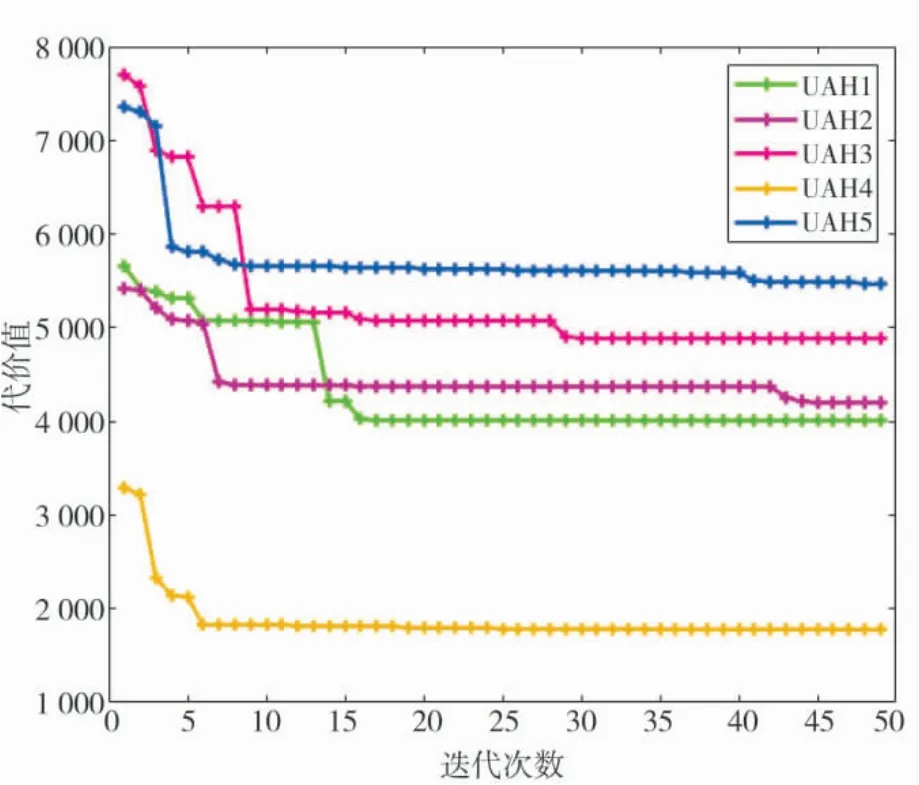
图17 基于HME-ABC 算法的每架UAH 航路代价值Fig.17 Cost value of each UAH flight path base on HME-ABC
图12、图15、图18 中3 种算法为UAH 编队的协同时间窗口.由图可知,ABC 算法与BAS-ABC 算法所规划的时间窗明显小于本文所设计的HMEABC 算法,而越小的时间窗意味着更高的任务执行难度.在相同约束条件下,HME-ABC 算法所规划的航路协同性更强,任务执行容错率更低.
上述分析表明,本文所提出的HME-ABC 算法能够利用异维记忆进化策略加快算法收敛速度,避免算法局部最优,有效地提高了传统ABC 算法的优化性能,快速高效地为UAH 编队规划出时间协同飞行航路.
4 结论
研究了一种基于异维记忆进化策略的人工蜂群算法用以解决多UAH 时间协同航路规划问题.该算法利用了蜜蜂的记忆能力与蜂群的信息交互能力,通过构建一个存储历史经验的记忆知识库来指导种群后续搜索与更新,提高了算法的收敛速度与优化效率.同时,基于跨越式搜索的侦察蜂更新策略也增强了传统ABC 算法的局部最优脱困能力.仿真结果表明,与传统ABC 算法相比较,HME-ABC 算法所规划的协同时间窗口宽裕度提高约72%,且算法迭代次数缩短约13%.

