基于多联盟非合作博弈纳什均衡搜索的集群对抗方法

刘 飞 董希旺,2 化永朝,2 于江龙 任 章

集群系统及集群智能的研究得到了广泛重视,其在集群编队、搜索救援、区域侦查等场景[1-3],以及军事领域具有极大应用潜力.军用无人集群系统具有分布式、自组织、自主决策的特点,面对常规防御系统可形成非对称优势.以无人集群拦截入侵集群是应对其威胁、抵消其优势的可行方式,由此形成了集群对抗这一研究课题[4].

多联盟非合作博弈理论可以用来建模与分析无人集群对抗中包含的复杂合作与竞争关系[5].大规模无人集群中可能会基于其载荷或性能特点形成各类异构子群,承担探测、干扰、攻击等不同任务.敌我无人集群均可基于上述特点或多样任务形成多个联盟.在多联盟非合作博弈框架下,每个智能体作为实际的决策者驱动其决策变量到达纳什均衡点,从而完成集群对抗任务.

多联盟非合作博弈建模了集群内的合作关系和集群间的非合作关系,其纳什均衡搜索算法的设计是实现集群对抗的关键.博弈参与者的策略由其动力学及控制输入驱动[6].对于具有动力学系统的多智能体系统的纳什均衡搜索算法设计,可利用时间尺度分离的方式依次进行静态纳什均衡的搜索和定点跟踪控制[7-8].另一种方法是直接设计分布式反馈控制器[9-10].针对部分信息未知的问题,通常基于一致性协议进行分布式状态估计[11-13].

无人集群的对抗中存在着大量的约束条件,主要来自资源或任务约束[14].含有约束的博弈问题的均衡被称为广义纳什均衡（generalized Nash equilibrium,GNE）.文献[15-17]提出了分布式的算子分割算法以定步长求解GNE,同时保证了算法收敛性.文献[18]研究了多联盟非合作博弈中GNE 的求解问题,考虑了代价函数和约束函数不光滑的情况.另一方面,集群对抗是一个高动态过程,无人集群的任务是时变的,因此,这种情况下多联盟非合作博弈的纳什均衡是一个轨迹,而不是一个静态策略[19],这对纳什均衡搜索算法的设计带来了更大困难.

本文主要研究基于多联盟非合作博弈的无人集群对抗的建模方法,提出多联盟非合作博弈时变纳什均衡的搜索策略,主要贡献总结如下：

1）考虑多联盟之间存在的耦合约束和局部约束,设计了一种障碍函数处理智能体的局部约束,可用于保证集群对抗的安全性.

2）将障碍函数引入博弈代价函数并转化为新的多联盟非合作博弈问题,证明了其广义纳什均衡是原问题的epsilon 广义纳什均衡.

3）基于障碍函数和原对偶方法设计了时变广义纳什均衡搜索算法.分析了该算法在集群对抗中分布式时变编队队形设计的应用.

1 问题的提出

1.1 多联盟非合作博弈模型

考虑集群博弈对抗场景下包含N 个联盟的多联盟非合作博弈广义纳什均衡搜索问题.

1.2 广义纳什均衡搜索

给出上述博弈问题的广义纳什均衡的定义.

对于所有的i∈P,j∈Pi成立,其中,.此外,如果存在集合Sij使得,对于任意的i∈P,j∈Pi和xij成立,那么是多联盟非合作博弈的纳什均衡.根据广义纳什均衡的定义,在满足约束的前提下,当各智能体采取广义纳什均衡策略时,没有一个参与者可以通过单方面改变策略来降低代价函数.

在无人集群的多联盟非合作博弈中,需考虑智能体的动力学特性,设智能体的动力学模型为无扰动的二阶积分器模型

关于通信拓扑、约束、代价函数有如下假设.

假设1:对于每个智能体联盟i,联盟内通信拓扑Gi是无向且连通的,联盟间通信拓扑也是无向且连通的.

假设2: 局部集合约束Ωij是闭凸集且边界是分段光滑的,联盟内耦合代价函数gij是凸函数且二次可微,满足Slater 条件.

假设4: 对每个智能体,其代价函数时变部分的一阶和二阶微分是有界的.

为便于求解多联盟非合作博弈的广义纳什均衡,引入变分不等式问题.

事实上,多联盟非合作博弈的广义纳什均衡同样也是上述变分不等式问题（5）的解.

引理1[6]: 在假设3 下,变分不等式问题（5）的任意一个解是多联盟非合作博弈问题（1）的广义纳什均衡.

引理2[6]: 假设变分不等式问题（5）满足Slater条件,那么x*是问题（5）的解当且仅当存在乘子,满足

对比式（6）和式（7）可见,区别在于式（6）中同一联盟i 中的对偶变量是相同的,即,因此,式（6）是式（7）的特殊情况.前面提到,伪梯度的强单调性保证了基于式（6）得到的广义纳什均衡的唯一性,且该广义纳什均衡属于满足式（7）的解的集合,特别地,将该广义纳什均衡称为变分广义纳什均衡.

本文主要研究多联盟非合作博弈的变分广义纳什均衡的搜索问题.变分广义纳什均衡的唯一性有利于纳什均衡搜索算法的收敛,同时也有着重要的结构和物理特性,即相同的对偶变量可使联盟中耦合约束带来的边界代价对于各个参与者是均衡的.由于多联盟非合作博弈的代价函数中引入了时变部分,博弈问题的纳什均衡不再是固定的点,而是时变的纳什均衡轨迹.因此,纳什均衡搜索算法要能够较好地寻找并跟踪纳什均衡轨迹,这也是一个具有挑战性的难题.

2 多联盟非合作博弈变分广义纳什均衡搜索问题转换

在多联盟非合作博弈的变分广义纳什均衡搜索中,智能体的动力学特性和局部约束的强制性是矛盾的,很难在满足动态搜索纳什均衡的过程中时刻满足局部约束.本章将设计一种障碍函数处理局部约束,将障碍函数引入代价函数中,从而将局部约束隐含在代价函数中,并得到新的多联盟非合作博弈问题.

2.1 局部约束的障碍函数

多联盟非合作博弈问题中参与者具有高阶积分器动力学特性或复杂动力学特性,文献中基于投影动态系统（projected dynamical system）稳定性设计的变分纳什均衡搜索算法不再适用.将根据局部集合约束设计障碍函数,使得纳什均衡搜索过程始终保持在局部约束范围内.

即便根据假设2,博弈策略的局部集合约束Ωij具有分段光滑边界,但是对于一般集合Ωij,很难找到表达其解析表达式.受优化理论中内点方法的启发,针对集合约束Ωij可设计障碍函数

从式（8）可见,对于某一决策变量xij,障碍函数有限表示决策变量满足局部约束,障碍函数为正无穷表示决策变量位于约束边界或不满足约束.障碍函数可以近似视为某个力场的势函数,当智能体的决策变量xij靠近约束边界时,由边界产生排斥力阻止其继续接近约束边界.对于任意形状的凸集合Ωij,很难找到完美的势函数,但是,后续分析将证明,式（8）的障碍函数可同样发挥势函数的作用,使得决策变量在多联盟非合作博弈纳什均衡搜索中始终满足局部约束.

对于完美的势函数,其势场力为其负梯度方向.当障碍函数作为近似势函数时,势场力为,其中,当在xij处可微时,为的梯度;当在xij处不可微时,为的次梯度.障碍函数（8）的性质由以下引理给出.

引理3: 在假设2 下,障碍函数（8）有以下性质:

如果xij在边界上有多个投影点,那么在xij处不可微,在xij处的次微分是集合的凸包.

2.2 ε-广义纳什均衡

通过引入障碍函数来处理局部集合约束,原多联盟非合作博弈问题可以转换为如下的博弈问题

对比问题（1）和问题（10）,可见问题（10）中障碍函数成为各智能体代价函数的一部分,而局部约束则放宽了边界条件.障碍函数将隐性地起到局部约束的作用,在广义纳什均衡搜索过程中,由于障碍函数的惩罚作用,智能体的决策变量会避免穿越局部集合约束边界.

后续将求解多联盟非合作博弈问题（10）,而非问题（1）.由于障碍函数的作用,问题（10）的纳什均衡搜索轨迹将始终保持在中,同时根据假设2,Slater 条件依然满足.

为了说明多联盟非合作博弈问题（10）和问题（1）的广义纳什均衡之间的关系,下面引入了ε-广义纳什均衡的概念.

下面的定理说明了多联盟非合作博弈问题（10）的解是问题（1）的一个ε-广义纳什均衡.

定理1: 在假设1-3 下,多联盟非合作博弈问题（1）和问题（10）均有唯一的变分广义纳什均衡.对于任意的ε>0,存在,使得问题（10）的变分广义纳什均衡是问题（1）的ε-广义纳什均衡.

证明: 在假设2 和3 下,多联盟非合作博弈问题（1）的策略空间约束满足Slater 条件,且代价函数伪梯度是强单调的,因此,基于多联盟非合作博弈问题（1）定义的变分不等式（5）存在唯一解.根据引理1,多联盟非合作博弈问题（1）的变分广义纳什均衡即为变分不等式（5）的解,同样满足存在性和唯一性.

对于多联盟非合作博弈问题（10）,每个智能体的代价函数改写为,根据引理3,是凸函数但不一定可微.可建立广义变分问题: 寻找,满足

根据式（13）,最终有

进一步,对于任意联盟i 中任意智能体j,可以定义类似的参数序列,对于任意的ε>0,可以找到一致的N,当选择n>N 时,以及参数组,多联盟非合作博弈问题（10）的变分广义纳什均衡是原问题（1）的ε-广义纳什均衡.这个结论很容易利用反证法证明.证毕.

3 分布式变分广义纳什均衡搜索算法设计与稳定性分析

在多联盟非合作博弈问题框架中,每个联盟中的智能体通过通信网络交互信息,并通过动态平均一致性算法,实时估计联盟代价函数对于各自决策变量的偏微分.采用原对偶方法处理联盟中的可分耦合约束,每个智能体均需估计各自的对偶变量,并引入了辅助变量zij以确保联盟内所有智能体对于对偶变量的估计是一致的.

无人集群的多联盟非合作博弈变分广义纳什均衡搜索算法设计为

定理2: 在假设1～3 下,x*是多联盟非合作博弈（10）的变分广义纳什均衡,当且仅当存在使得是系统（15）的平衡点,其中,.

是系统（15）的平衡点,则有

根据引理1 和引理2,x*是多联盟非合作博弈问题（10）的变分广义纳什均衡当且仅当存在满足下述KKT 条件

因此,下面主要证明条件（16）～条件（19）与条件（20）～条件（21）的等价性.

对上述李雅普诺夫函数函数求导,利用假设3和4,可依次证明级联系统的输入状态稳定,并且系统状态收敛到纳什均衡的邻域内.

在多联盟非合作博弈变分纳什均衡搜索算法（14）中,直接使用了所有智能体决策变量的完全信息x 和v,所以策略（14）不是完全分布式的.事实上,类似对联盟代价函数梯度的估计,可以利用领导者-跟随者一致性算法估计其他智能体的状态信息,并用来计算代价函数偏微分和约束函数数值.

4 集群时变编队干扰与反干扰对抗

4.1 集群时变编队跟踪的决策－控制架构

本节将介绍多联盟非合作博弈纳什均衡搜索算法在分布式时变编队控制中的应用.

假设敌我双方无人集群分别形成一个任务联盟,每个联盟内分别有一个领导者,联盟中跟随着进行时变编队跟踪以完成联盟任务.在已有文献中,时变编队队形通常是指定的全局信息,本文通过多联盟非合作博弈纳什均衡搜索给出时变编队队形决策.假设我方联盟P1中每个智能体均搭载有电磁干扰装置,需与联盟中其他智能体协作以产生对敌方联盟P2最大干扰效果.联盟P2则处于防御态势,尽量形成紧密阵型维持联盟内通信拓扑的连通性.在这一场景下,两个联盟均需协调联盟内智能体的策略,并找到各自最佳时变编队队形.

此外,各联盟需满足一些约束条件.要求联盟中智能体与领导者的平均距离存在最大阈值以减小通信能量损耗.每个联盟内任意一个智能体有活动范围限制,该活动范围是以领导者为圆心,给定半径的球,从而引入了联盟中智能体的局部约束.

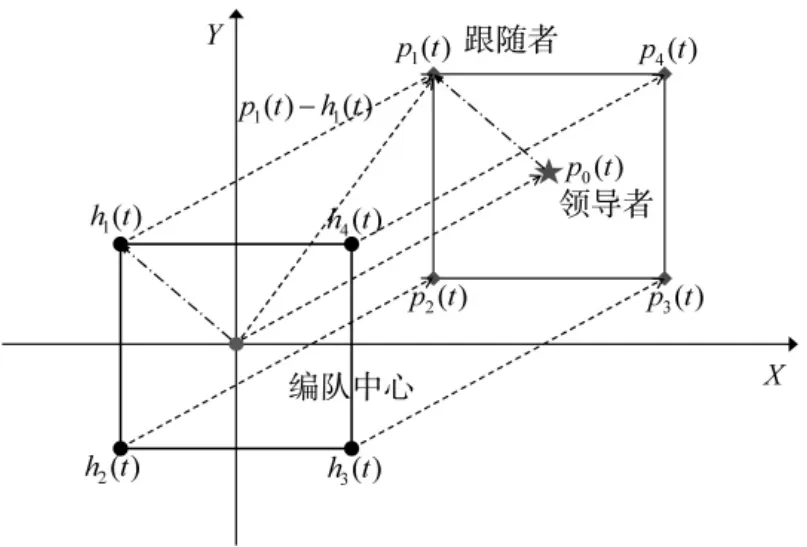
图1 时变编队跟踪示意图Fig.1 Schematic diagram of time-varying formation tracking

多联盟非合作博弈变分广义纳什均衡搜索—分布式时变编队跟踪控制构成了决策—控制的双层结构,如图2 所示.多联盟非合作博弈变分广义纳什均衡搜索算法给出跟随者最优编队构型,随后由编队跟踪控制算法实现.领导者作为独立节点,是编队跟踪的目标,也是编队构型决策的参考点.

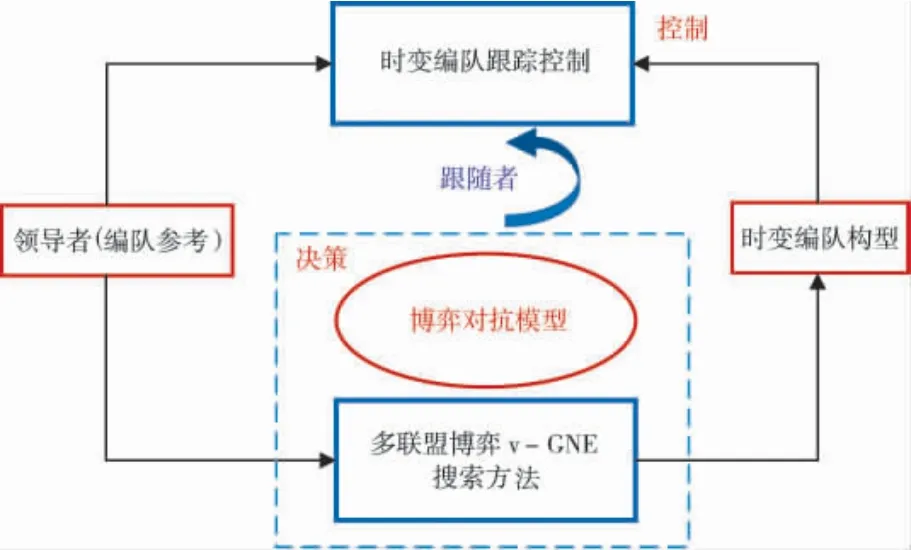
图2 时变编队构型决策—编队跟踪控制层次结构Fig.2 Hierarchy structure of time-varying formation decisionmaking and formation tracking control

在上述博弈问题的代价函数定义中,假设联盟P1的领导者是运动的,因此,代价函数与领导者的坐标有关,博弈问题的纳什均衡是时变的.基于纳什均衡搜索算法（14）以及编队构型的动力学模型（2）可输出时变编队构型,编队构型的一阶导数,以及二阶导数,其中,等于纳什均衡搜索算法（14）给出的控制量.在此基础上可设计联盟P1的编队跟踪控制器,在跟踪的同时实现时变编队构型的保持.

智能体动力学仍为二阶积分器模型,时变编队跟踪控制器设计由文献[2]给出,其形式为:

4.2 仿真算例

在无人集群干扰及反干扰对抗场景以及多联盟非合作博弈模型基础上,应用多联盟非合作博弈纳什均衡搜索算法（14）以及编队跟踪控制算法（24）,仿真结果如图3～图5 所示.图3 给出了集群博弈对抗双方轨迹曲线.联盟P1跟随其领导者环绕联盟P2作圆周运动.两个联盟根据干扰与反干扰作战任务和博弈模型实时求解编队构型,在近似收敛到时变纳什均衡后,联盟P1在其领导者轨迹内侧,抵近联盟P2施加干扰,而联盟P2则远离联盟P1,两个联盟的运动形成了环绕联盟P2中心节点的运动模式.

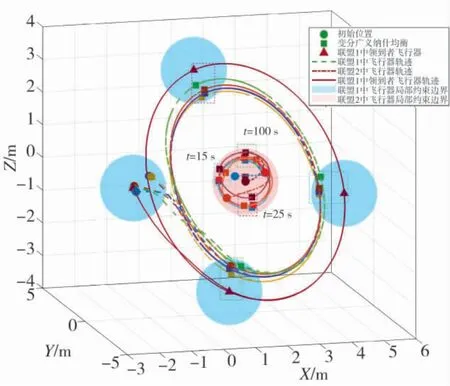
图3 时变编队跟踪干扰-反干扰场景下集群博弈对抗双方轨迹Fig.3 Trajectories of both sides of cluster game confrontation in the time-varying formation tracking interference and anti-interference scenario

两个联盟的状态曲线如图4 所示,不同于静态纳什均衡,本例中纳什均衡是时变的编队构型,由于联盟P1的领导者为规律的圆周运动,可见各联盟智能体的状态也是周期性变化.联盟的耦合约束如图5所示.由于收敛误差的存在,联盟P1、P2的耦合约束围绕0 附近上下波动.理想结果应当是耦合约束渐进收敛到0,可通过RISE 方法设计纳什均衡搜索策略,这会是本文后续的研究方向.

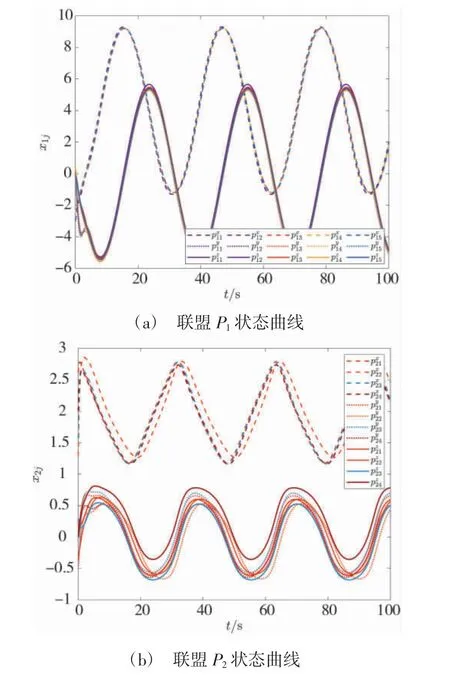
图4 时变编队跟踪干扰-反干扰场景下集群博弈对抗双方轨迹Fig.4 Trajectories of both sides of cluster game confrontation in the time-varying formation tracking interference and anti-interference scenario

图5 时变编队跟踪干扰－反干扰场景下联盟耦合约束Fig.5 Coalition coupling constraints of agents in the time-varying formation tracking interference and anti-interference scenario

5 结论

本文研究了严苛多约束下多联盟非合作博弈变分广义纳什均衡搜索算法及其在无人集群博弈对抗中的应用.在多联盟非合作博弈中,智能体决策变量存在局部约束,以及联盟内的耦合约束.为使得决策变量始终满足局部约束,设计了一种障碍函数,其满足凸性和可微性.随后,设计了多联盟非合作博弈变分广义纳什均衡搜索算法,证明了搜索算法的平衡点等价于变分广义纳什均衡点,在多联合非合作博弈目标函数为时变的情况下,变分广义纳什均衡搜索算法可以收敛到变分广义纳什均衡点的邻域.最后设计了集群干扰与反干扰的对抗场景,验证了多联盟非合作博弈变分广义纳什均衡搜索算法在该场景中的应用能力.