无人机集群反制与对抗技术探讨

任 智 张 栋 唐 硕 王孟阳 李智军

无人机集群作战是网络化智能化作战的重要模式,能够借助数量优势实现大范围区域覆盖的多源感知与任务执行,在体系对抗中占据战场优势[1].无人机集群系统在复杂多变的战场环境中具有强大的战场生存力、环境适应力和快速响应力.给现有的防空体系带来极大的颠覆与挑战,出现“打得上的打不起”和“打得起的打不上”的对抗难题[2].因此,无人机集群系统反制与对抗是未来体系化作战的研究重点.

由于无人机集群系统成本低、规模大、机动性能强,传统地面防御系统难以经济有效地应对集群目标威胁,常见的集群反制对抗措施主要通过物理攻击或电子干扰等方法破坏集群系统网络节点或通信链路.对此,中国电子技术标准化研究院2021 年发布的《智能无人机群系统发展白皮书》根据不同任务与应用场景,对无人机集群系统的稳定性、可靠性、安全性提出了不同层级的要求,以保证集群系统在有限通信与复杂环境下的作战能力[3].由此可见,随着复杂场景下集群控机技术的发展,“硬杀伤”与“软杀伤”等方法对无人机集群的反制效果有限.因此,交战双方集群间的智能化与体系化对抗是未来集群反制与对抗的主要途径与发展趋势.

集群对抗问题的研究最早在博弈论中的疆土防御[4-6]与追逃博弈[7-9]问题中展开,由于集群对抗博弈的局中人规模大导致求解困难,有学者通过目标分配方法将集群对抗问题转换为一对一或二对一的问题,进而规划集群个体的作战任务与机动轨迹[10-12].虽然基于目标分配的集群对抗博弈模型简化方法能够在一定程度上降低模型求解的计算复杂度,但是并没有考虑目标分配后各子集智能体间的相互作用,不能够体现大规模无人机集群协同作战与集群智能的特点.因此,也有学者从多智能体系统理论[13-14]与网络动力学[15-16]的角度出发,为每个智能体设计独立的个体行为与自组织决策规则,本文根据无人机集群对抗的典型场景、任务需求与作战流程,从复杂群体行为演化控制、敌方集群统计特征识别推断以及集群博弈对抗机理的角度出发,探讨无人机集群对抗的基本模型与关键技术,分析了集群对抗问题研究的难点与挑战.

1 集群对抗问题与相关概念

在集群对抗过程中,无人机集群系统通过个体间相互作用的分布式自主决策涌现出复杂的集群行为与协同战术,根据战场环境实时态势、敌方集群策略与实际对抗任务需求,实现战场快速响应与集群作战目标.对此,本文提出了涵盖群体动力学模型、对手建模问题和集群博弈对抗的集群对抗基本模型与体系框架,如图1 所示.

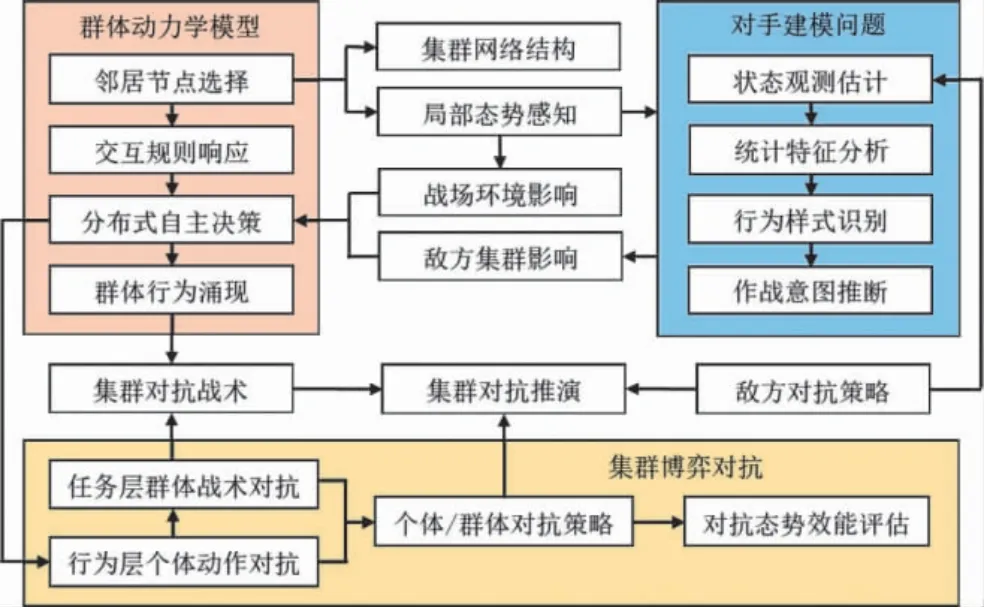
图1 集群对抗体系框架Fig 1 Swarm confrontation system framework

其中,群体动力学模型在确定集群网络结构与相互作用关系的基础上,设计集群个体间交互规则响应与分布式自主决策方法,分析集群智能行为的涌现过程与演化机理.然后进一步考虑未知的敌方对抗策略进行对手建模,根据局部态势感知信息实现对敌方集群的状态观测估计与网络结构辨识,推断敌方集群采取的行为样式与作战意图,进而采取有针对性的对抗策略.最后,集群对抗博弈模型在群体动力学模型与对手建模的基础上考虑战场环境与敌方集群行为的影响,根据集群对抗任务耦合的作战效能指标,评估从个体自主决策到群体对抗策略的对抗效果.在此基础上,进一步优化集群个体自组织规则与分布式自适应决策,引导集群系统群体行为与集群智能的涌现,提高集群对抗的响应速度与决策效率.

结合集群对抗过程中无人机集群携带机载雷达、电子干扰设备与机载武器等有效载荷的特点,构想集群对抗典型作战场景如图2 所示.假设交战双方出动大规模无人机集群进攻敌方地面目标,同时在交战对抗中对敌方集群目标展开突防拦截.交战双方都需要在保证己方阵地安全的基础上首先实现对敌方阵地的饱和打击,其次尽可能地减少己方无人机的损毁并增加敌方有生力量的消耗.

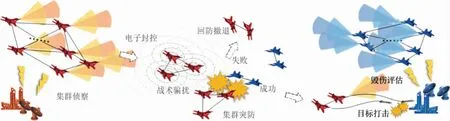
图2 集群对抗典型作战场景Fig 2 Typical battle scenario of swarm confrontation

在对抗的初始阶段,作战双方通过地面指挥控制中心的预警雷达实现阵地区域覆盖扫描,探测并预警敌方集群目标.由于地面预警雷达覆盖面积大,扫描周期长,对敌方大规模集群目标的预警信息时效差、精度低,仅能够为我方集群提供较为粗略的战场态势信息.因此,无人机集群还需要结合作战环境与己方拒止区域等掩护,采取合适的编队构型与接敌策略执行集群侦察任务,锁定跟踪探测范围内的敌方目标,并通过集群内个体间通信组网的信息交互,实现战场多源态势感知融合,获得更为精确的战场态势信息.在此基础上,无人机集群可根据实时作战态势选择执行电子封控任务或战术骗扰任务,为集群突防提供更有利的作战优势.随着对抗双方交战进程的推进,无人机集群结合对抗结果与实时态势,根据自主决策规则确定当前的作战任务与机动策略.若集群突防成功,则可以考虑追击敌方目标并执行既定打击任务；若集群突防失败,则可以考虑执行回防撤退任务四散逃逸并回防阵地.在对抗的结束阶段,态势占优的一方通过集群对抗战术完成了既定战术任务目标,由存活的无人机集群对当前战场态势进行快速评估,并将实时态势信息回传给地面指挥控制中心,根据对抗评估结果决定下一周期的集群作战任务目标.

2 集群对抗基本模型

2.1 群体动力学演化与控制模型

在集群对抗过程中,如何描述个体到群体行为的演化关系与群体智能的涌现机理,是研究集群对抗问题建模的关键.集群系统个体在空间中的分布与群体行为建模的主要方法包括空间法和非空间法[17],如表1 所示.其中,空间法着眼于集群系统的空间分布规律,将集群系统视为连续整体,采用概率密度分布描述集群系统的运动与状态变化[18]；非空间法则从个体的运动学与动力学模型出发,通过描述个体与环境或其他个体行为的相互作用,确定集群系统个体的运动状态[19].由于实际宏观集群系统中个体的运动学与动力学特征不可忽略,难以满足空间法对群体的连续性假设,因此,群体动力学建模从个体运动学与动力学模型出发,考虑集群个体间的相互作用与感知决策,描述集群系统在空间内的运动状态与内部动力学响应,对应集群个体的行为响应与决策流程如图3 所示.

表1 群体动力学建模空间法与非空间法的异同Table 1 Similarities and differences between spatial and non-spatial methods of group dynamics modeling

图3 个体行为响应与决策流程Fig 3 Individual behavior response and decision-making process

集群个体首先根据自身感知交互能力定位其他集群节点,然后选取满足个体通信约束与感知边界的邻居节点建立动态连通的集群拓扑网络.在邻居节点位置、速度等运动状态的影响下,集群个体根据既定的自组织规则与控制协议确定各自的行为策略.在此基础上,集群系统通过上述动作状态转移与邻居节点交互响应,实现对应既定交互规则的复杂集群行为演化.集群系统的内部响应机理与复杂行为演化机制最早在生物集群研究中展开,通过分析鱼群[20,21]、鸟群[22]与鸽群[23]等生物集群行为,研究不同生物集群中个体相互作用关系的建立与复杂集群网络的形成,提出了不同生物集群的邻居节点选择方式与对应集群网络的拓扑结构,如表2 所示.表中邻居节点示意图的红色节点表示当前节点,蓝色节点表示邻居节点,白色节点表示集群系统其他节点,箭头代表节点当前速度方向,阴影部分代表了对应邻居节点选择方法考虑的约束条件边界.

表2 集群网络拓扑连通与邻居节点选择方式Table 2 Swarm network topology connection and neighbor node selection mode

实验物理学家从统计力学的角度出发,进一步总结了生物集群的自组织规则与相互作用规律.Reynolds 等首先提出了集中、防碰撞与速度匹配3个个体间相互作用规则,并据此建立Boid 模型模拟集群系统速度一致的聚集行为[24].在此基础上,相关研究从多智能体系统、平均场理论、复杂网络理论和最优控制理论等角度出发,通过设计集群系统中个体的简单交互规则,确定集群系统的局部信息交互方式与个体间相互作用规则的行为响应流程,分别提出了自驱动粒子模型、异质平均场模型、引力/斥力势模型、一致性控制模型和最优控制模型等各类不同的群体动力学模型[25-30].在此基础上,进一步研究了模型中不同个体相互作用规则对集群系统动态演化过程与复杂集群行为涌现结果的影响,然后通过相应的集群控制方法实现集聚、涡旋与分簇等不同群体行为的自组织控制与自适应切换[31].典型集群动力学模型的对应自组织规则与集群行为如表3 所示,集群动力学模型的自组织规则描述了集群个体间的相互作用关系.在此基础上,集群系统能够通过根据既定自组织规则在宏观层次上涌现出各类复杂的集群行为.对此,Olfati-Saber 等通过设计式（1）所示一致性协议与个体间相互作用的势函数[29],实现集群系统集聚与跟踪等复杂集群行为的自组织控制：

表3 集群动力学模型自组织规则与集群行为Table 3 Self-organizing rules and swarm behavior of swarm dynamics model

式中,xi∈R3和vi∈R3表示集群系统个体位置和速度矢量;σ 为正则化梯度函数;ε 为对应正则化梯度函数参数;aij为对应邻居节点相互作用强度;φα为对应集群个体间邻居节点相互作用的势函数.在上述模型与集群个体自组织相互作用规则中,通过设计正则化梯度函数σ 的对应参数ε,可以实现集群系统集聚、涡旋、极化与分簇等复杂群体行为,进而实现蜂拥、盘旋、编队、跟踪与避障等集群作战任务.

2.2 敌方集群统计特征模型

集群系统空间分布特征可以采用聚类方法对观测的目标位置信息进行统计分析,通过对观测集群目标的子群分簇质心与形状的估计与拟合实现对集群目标空间分布特征提取与分析[32].常见的聚类方法包括K-means 聚类方法与EM 聚类方法（expectation maximization,EM）.其中,K-means 聚类方法根据集群个体间样本距离将观测集群目标划分为若干个子群,具有较高的计算效率,能够实现指定子群个数的快速聚类,但仅能够确定集群整体的空间分布,无法确定对应各分簇子群的形状与质心[33].而EM 聚类方法则采用期望最大化算法（expectation-maximization algorithm）,通过期望（E 步）和最大化（M 步）两个步骤的迭代更新,能够实现对观测目标集群子群的分布估计[34].假设集群空间分布由k 个高斯分布组成,对应高斯混合分布函数：

式中,xi为对应集群状态总体X 的m 个观测样本;ai为对应第i 个高斯分布的混合系数;为对应高斯分布概率密度函数;μi和σi为对应第i 个高斯分布的均值向量与协方差矩阵.则对应观测目标xj∈X从属于第i 个高斯分布的后验概率为：

集群系统运动状态的统计特征参数主要包括速度一致性序参量、群体角动量和群体极化程度[35].其中,VISCEK 等首先定义了集群个体速度矢量的加权平均参数[25],用来描述集群中不同个体运动速度的一致性程度,如下式所示：

式中,va为速度一致性序参量;m 为观测的集群目标个体数目;vi为对应个体i 的速度矢量,对应集群系统个体运动状态与速度波动与群体的规模分布存在空间关联关系如下式所示[36]：

群体极化程度和群体角动量[21,27]针对集群系统中不同个体的运动状态与速度方向特征,定义了集群个体运动速度方向的一致程度和集群整体运动速度方向的旋转程度如下式所示：

式中,ui为对应个体i 的单位速度矢量；ri为对应个体i 指向集群质心的矢径；Op为群体极化程度,表征了集群中不同个体运动速度方向的一致性程度；Or为群体角动量,表征了集群中不同个体绕集群质心运动的旋转程度.Op越大,则表征集群不同个体的速度方向一致性程度高;Or越大,则表征集群不同个体绕质心的旋转程度越大.

对此,结合生物集群的实验观测统计数据信息,可以进一步将集群系统涌现的集聚、涡旋与极化等复杂行为与群体状态映射到集群系统运动状态的序参数取值范围,总结如下集群行为状态的唯像规律[21].因此,通过分析群体极化程度与群体角动量的统计特征与变化规律,能够在识别目标集群运动状态的基础上进一步推断目标集群的行为样式.在此基础上,可以进一步定义集群行为涌现的表达熵（expressive entropy）[37]来描述对应各类统计特征参数识别与推断集群行为样式的不确定性,如下式所示：

式中,Sp为对应集群系统的各类统计特征参数；Hexp为表达熵,表征了通过各类统计特征参数分析集群行为涌现的不确定性；M（Sp）为对应各类集群行为样式b 的集合；p（b）为对应各类统计特征参数识别与推断集群行为样式b 的概率.

2.3 集群对抗态势效能模型

在无人机空战对抗问题中,集群系统的空战对抗态势效能评估[38]涵盖了战场空间态势、作战任务能力和体系对抗效能.通过考虑集群网络相邻节点的协同效应与集群系统协同作战的空间态势,分析交战双方集群系统在攻击占位或防御机动等方面的作战优势,衡量交战双方采取方采取对抗战术意图的优劣与威胁程度.

集群对抗的战场空间态势在一对一作战态势的基础上考虑集群个体间的协同效应.一对一对抗的战场空间态势评估根据交战双方相对位置与速度方向,将对应战场空间分布的迎头态势和尾追态势分为均势、优势与劣势.通过结合自身任务作战能力的机动性能约束、侦察感知范围和毁伤打击边界,基于专家经验设计对应个体i 与个体j 的角度态势、距离态势、高差态势和速度态势等态势函数[39].集群个体各类战场空间态势函数的具体数学模型因专家经验相异而各不相同,常通过非线性函数的组合描述集群个体对抗态势的空间分布规律与特征.在此基础上,将集群对抗中每组个体间的战场空间态势以矩阵形式描述,如下式所示：

式中,Sk为对应各类战场空间态势的态势矩阵;sij为个体i 与个体j 间的相对态势.

在对抗过程中,集群系统首先根据当前战场空间分布与运动状态将敌我双方集群个体划分为若干分簇子群社团,不同子群的个体在战场中的空间态势互不影响[40].假设同一子群中的个体仅能够选取同一敌方子群中的个体作为对抗目标,对抗目标相同的集群个体战场空间态势相互独立且形成协同作战态势[41],则对应集群个体的协同作战态势如下式所示：

式中,Rj为以敌方个体j 为对抗目标的集群个体集合;Jsi为对应个体i 考虑协同效应的战场空间态势,表征了具有相同对抗目标的集群个体间存在协同效应,可以通过相互配合形成协同机动策略,提升集群对抗整体战场空间态势与作战效能.

此外,集群个体间确定的协同关系与目标分配结果影响了集群系统整体的目标杀伤率、装备生存率和作战效费比等体系对抗效能.其中,目标杀伤率和装备生存率与集群个体雷达探测系统的预警概率和机载武器系统的毁伤概率有关.在集群对抗过程中,集群系统个体对目标的探测预警与毁伤打击过程相互独立,则以敌方集群个体j 为对抗目标的我方集群个体i∈Rj协同打击的毁伤概率为：

式中,pf,ij为集群i 个体雷达探测系统发现对抗目标j的预警概率；pd,ij为集群个体i 机载武器系统对打击目标j 的毁伤概率.

根据集群个体通过协同配合对目标的杀伤概率,定义集群在对抗过程中对敌方目标总体杀伤概率与敌方目标总体数量的比值为集群对抗的目标杀伤率,如下式所示：

同理,定义集群系统在敌方攻击下存活概率与集群个体总数量的比值为集群系统的装备生存率,如下式所示：

式中,pd,ji为敌方集群个体j 机载武器系统对我方集群个体i 的毁伤概率.在此基础上,进一步定义集群系统对抗过程中对目标杀伤率与己方集群个体在敌方攻击下毁伤概率的比值为集群系统完成既定作战任务的效费比[42],如下式所示：

在集群对抗的战场空间态势与体系对抗效能的基础上,进一步考虑敌我双方集群系统在机动响应、感知探测、毁伤打击和电子对抗等方面的整体作战能力优势与劣势.针对各类集群对抗态势效能,采用加权方法确定对应集群系统个体的综合协同态势函数如下式所示：

式中,Js为对应集群系统角度态势、距离态势、高差态势和速度态势的战场空间协同态势；Je为对应集群系统机动响应、感知探测、毁伤打击和电子对抗的整体协同作战任务优势；Jc为对应集群系统体系对抗效能；ωs、ωe和ωc分别为对应各类型态势效能的加权系数.

3 集群对抗关键技术

结合无人机集群对抗过程中感知、决策与控制的具体作战流程,在集群对抗中敌方集群统计特征模型、集群对抗态势效能模型和群体动力学演化与控制模型的基础上,从敌方集群建模、动态博弈决策和集群协同控制的角度出发,确定集群对抗关键技术包括基于多源态势感知的对手建模方法、面向不完全信息动态博弈的集群对抗决策方法和结合虚拟领导者的分布式集群牵制控制方法,具体内容如图4 所示.

图4 集群对抗基本模型与关键技术Fig 4 Basic model and key technology of swarm confrontation

3.1 结合虚拟领导者的集群牵制控制

在高动态强对抗的复杂战场环境中,面对突发敌方威胁时集群个体需要快速机动响应实现既定作战任务的集群控制.牵制控制方法能够根据集群系统的群体动力学模型,通过对集群部分节点的控制实现在保证集群网络最小功能单位持续连通的条件下集群系统作战任务与群体行为的牵制控制[43].其中,关键牵制节点的选取根据对应分簇子群网络节点度量参数来确定,而虚拟领导者根据集群系统期望的空间分布与运动状态来确定.在对应博弈模型纳什均衡解的基础上,通过确定△T 时刻后集群系统最小功能单位的分簇子群,选取对应分簇子群的群体质心为虚拟领导者,虚拟领导者在当前时刻的速度即为△T 时刻后对应分簇子群精炼贝叶斯纳什均衡策略的平均速度.设对应第k 个分簇子群有nk个节点,则对应虚拟领导者k 的动态方程如下式所示：

式中,xk和vk为集群分簇子群k 中虚拟领导者k 的位置矢量和速度矢量；为对应集群对抗博弈模型中个体i 的精炼贝叶斯纳什均衡策略；ui为对应个体i 的单位速度方向矢量.

在此基础上,集群系统通过虚拟领导者对关键节点的牵制引导与集群网络相邻节点间的相互作用影响,实现对应集群系统群体行为与对抗战术等期望目标的牵制控制.对应集群系统各节点的运动学与动力学模型如下式所示：

式中,xik和vik为集群分簇子群k=1,2,…,m 中集群个体i=1,2,…,ni的位置向量和速度向量；为对应集群个体i 受同一分簇子群中邻居节点个体j∈Ii影响的速度方向控制输入；为对应集群个体受虚拟领导者k 影响的控制输入；α 为对应集群个体是否为关键牵制节点的判断标识,若α=1 则该个体为关键牵制节点,在虚拟领导者的引导信息下不受其他集群个体节点的影响.

在此基础上,设计对应各节点间相互作用下的控制输入如下式所示：

式中,第1 项表征了群体动力学模型中远距吸引、近距排斥的相互作用规则；第2 项则表征了群体动力学模型中速度匹配的相互作用规则；k1,k2为对应各类相互作用规则的权重系数；Ni为节点i 的邻居节点集合;为对应集群网络拓扑连通关系的邻接矩阵;ψ 为对应集群个体间引力/斥力相互作用的人工势函数,在不同集群动力学模型中具体的数学形式各不相同.

集群对抗问题中结合虚拟领导者的集群牵制控制流程如图5 所示,集群系统首先根据当前时刻敌我双方集群状态实时优化网络结构与拓扑重构.在此基础上,根据期望的集群系统空间分布与运动状态划分集群分簇社团,通过计算网络节点度量参数确定集群网络的关键节点.然后,根据集群系统关键节点与其他网络节点信息反馈,确定虚拟领导者与网络节点的控制输入.最后,通过集群系统网络节点的空间分布与运动状态更新实现集群对抗的作战推演与节点更新.

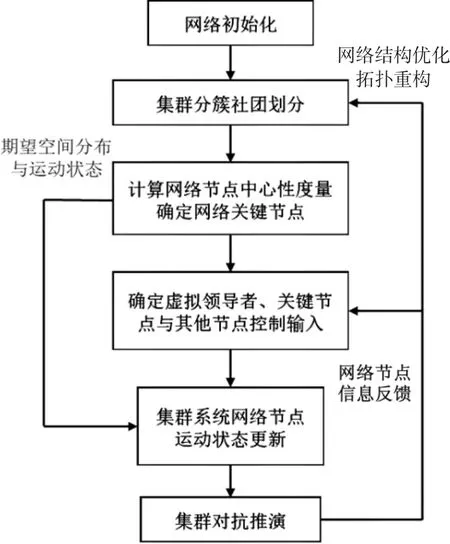
图5 集群对抗牵制控制流程示意图Fig 5 Flow diagram of swarm confrontation pinning control

3.2 基于有限观测信息的对手建模

集群对抗的对手建模从个体运动状态、群体协同行为与集群战术意图出发,通过对敌方集群系统的观测信息推断敌方集群系统模型[44].其中,敌方集群系统的空间分布与个体运动状态信息可以通过局部态势感知确定,在此基础上根据有限观测信息实现敌方集群系统模型的推断.

由于集群系统时序状态信息的变化规律能够反映集群系统采取的战术意图,因此,考虑采用动态贝叶斯网络方法分析敌方集群的统计特征,推断敌方集群行为与作战意图[45].设状态变量与观测变量

,则动态贝叶斯网络可表示为状态变量与观测变量的联合概率分布:

将动态贝叶斯网络分为决策层和特征层两层结构.其中,特征层选取集群个体速度V、偏航角φ 和高度h 作为观测节点,表征了对应空间分布与运动状态的变化特征与规律；决策层选取集群系统宏观群体行为M 和作战意图A 作为状态节点,表征了对应聚集、盘旋与分簇等复杂集群行为,以及合围打击、战术骗扰与集群突防等集群对抗作战战术.设t-1 时刻的底层状态与观测节点信息序列为e1:t,顶层决策节点滤波结果为At,根据设计动态贝叶斯网络的链式结构,结合式贝叶斯公式与链式推理规则可得t 时刻顶层决策节点At采取战术意图的条件概率如下式所示:

针对有限观测信息对手建模问题的动态贝叶斯网络推理过程如图6 所示.集群系统首先根据获取敌方集群的有限观测信息进行多源数据融合与目标关联处理,为对手建模的集群行为识别与作战意图预测提供实时输入数据.在此基础上,动态贝叶斯网络进行网络参数初始化并确定对应状态节点的条件概率与转移概率,然后更新贝叶斯网络节点概率分布,实现敌方集群系统状态特征提取与行为意图识别.

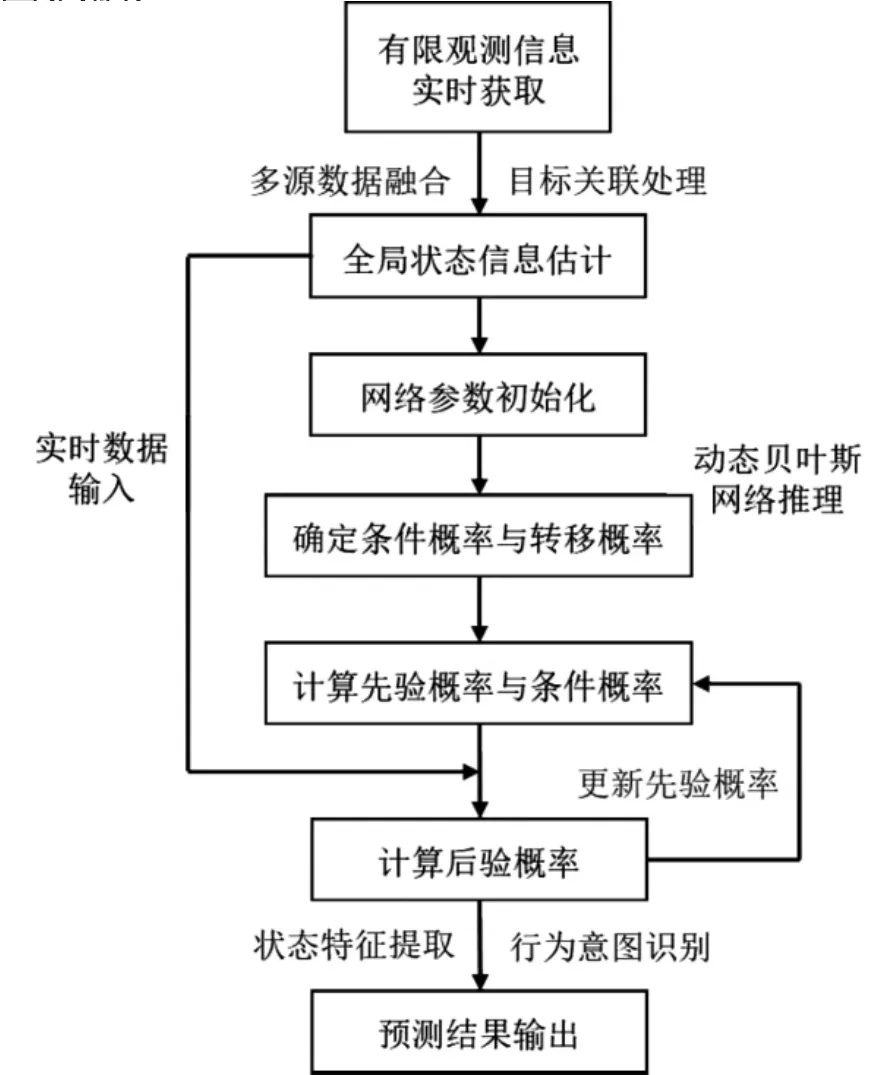
图6 动态贝叶斯网络推理流程示意图Fig 6 Flow diagram of dynamic Bayesian network inference

3.3 面向集群对抗的不完全信息动态博弈

博弈模型的不完全信息专指局中人在博弈开始前对其他局中人的事前信息了解不充分,这些事前信息泛指能够影响博弈局势的局中人属性[46].在集群对抗问题中,由于双方遭遇交战时并不清楚对方的群体动力学模型与态势效能评估依据,因此,可以将集群对抗博弈模型中的不完全信息定义为集群系统个体的作战意图偏好,在对手建模结果的基础上,通过海萨尼转换引入虚拟局中人“自然”,赋予博弈中各局中人的作战偏好类型与对应概率密度[47],表征了集群系统在当前态势下的作战偏好是更倾向于保守策略还是激进策略.

式中,gb为对应蓝方集群系统对当前战场态势的评估结果;At为对手建模中对应t 时刻动态贝叶斯顶层决策节点滤波结果;e1:t为对手建模中对应t-1 时刻的底层状态与观测节点信息序列.

式中,V 为对应博弈模型中采取相应策略的效用函数;πk为对应局中人采取的混合策略组合;为集群协同态势效能评估函数;s 为对应局中人采取混合策略的动作状态转移.

不完全信息动态博弈模型的精炼贝叶斯纳什均衡是推断概率和混合策略组合共同组成的策略评估,是完全信息动态博弈子博弈精炼纳什均衡与不完全信息静态博弈贝叶斯纳什均衡的结合[48].对此,集群对抗博弈模型的精炼贝叶斯纳什均衡定义如下：设是局中人在全部博弈阶段中的某一混合策略组合序列,是除此局中人i 外其他局中人的全部混合策略组合序列.若对每一个局中人i在全部博弈阶段任意策略组合序列都有：

针对集群对抗问题的不完全信息动态博弈过程如图7 所示.集群对抗采用海萨尼转换将不完全信息动态博弈转换为完全不完美信息动态博弈,通过自然确定局中人概率分布并采用贝叶斯估计推断敌方未知属性与概率分布.在此基础上,集群系统通过协同战术意图决策进行动作状态转移,并根据效用函数求解对应贝叶斯纳什均衡的集群对抗协同策略.

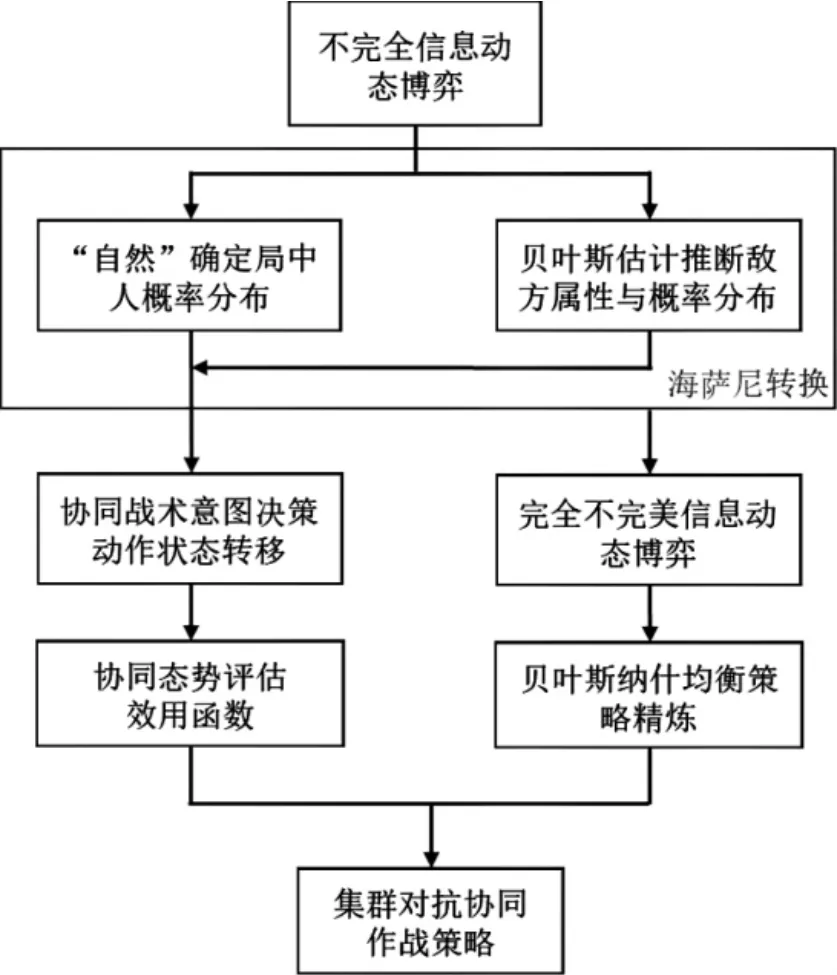
图7 集群博弈对抗流程示意图Fig 7 Flow diagram of swarm game confrontation

4 研究难点与挑战

4.1 动态对抗过程中集群网络的即时修复

集群拓扑网络结构的连通性与鲁棒性是集群系统发挥协同作战效能的关键.在高动态强对抗的作战过程中,集群系统复杂行为的形成与群体智能的涌现依赖于集群系统的持续连通与信息交互.现有的网络结构优化设计与拓扑重构研究主要针对无线传感系统与电网配电系统等问题[49-50].由于传感器网络和电网系统中的节点不具备移动能力,静态网络节点构成的固定网络系统能够预先确定各节点的重要程度,根据复杂网络性质将网络节点分为关键节点、冗余节点和普通节点3 种不同类型.在此基础上,针对不同类型节点的失效情况预先设定对应网络节点故障的重构策略与方案.在对抗过程中,集群网络节点的空间分布与个体的运动状态在高度动态变化,各节点在集群网络中的重要程度与对应节点类型也随之发生变化.传统网络重构与优化方法难以适应无人集群系统的动态性场景与实时性要求,需要进一步研究集群网络的在线故障诊断与即时修复策略,在网络故障诊断结果的基础上定位失效节点类型与其对应的邻居节点,由其中冗余节点自组织代替失效节点,实现集群网络的信息交互与作战能力的自适应恢复.因此,集群系统网络的在线重构与即时修复是群体动力学模型未来实际应用中关键难点与挑战.

4.2 局部感知下敌方集群的全局状态估计

对手建模问题一方面需要对多源局部态势感知信息进行融合处理获得敌方集群整体统计特征等战场态势信息；另一方面需要根据敌方集群的空间分布与运动状态信息推断敌方整体集群的行为样式与作战意图[51].而集群对抗的交战双方在遭遇时仅能通过个体的局部观测获取敌方集群个体的状态与位置信息,往往无法直接获取敌方集群的全局空间分布与运动状态信息.传统的数据融合与目标关联算法研究主要集中在多传感器多目标跟踪问题[52],通过滤波方法对同一时刻多传感器的探测信息进行融合处理,实现对多个目标的状态定位与估计.在此基础上,采用目标关联算法实现对不同时刻多目标跟踪的数据关联,通过计算相似度函数确定当前探测目标与已形成轨迹跟踪目标之间的关联概率.由于集群对抗过程中,不同时刻个体节点观测到的敌方目标数量与对应位置动态变化.传统数据融合与目标关联算法对无人集群系统观测数据偏差的敏感度更高,数据融合的准确性与目标关联的成功率难以保证.因此,集群系统在局部观测下对敌方集群整体的全局状态估计是对手建模的核心难点与挑战.

4.3 多阶段博弈对抗纳什均衡策略的精炼

集群系统的博弈对抗具有较长的对抗过程与博弈阶段,对应集群对抗的分布式不完全信息动态博弈模型可能存在多组混合策略组合序列满足纳什均衡条件.因此,集群系统多阶段博弈对抗需要结合集群对抗的具体作战任务需求,实现对博弈模型纳什均衡解的精炼.由于集群对抗问题中集群的作战规模大,对应博弈模型精炼纳什均衡的计算复杂度高且求解困难.传统的分布式不完全信息博弈模型纳什均衡求解与精炼主要采用反事实遗憾值最小化算法（counterfactual regret minimization,CFR）[53],通过遗憾值表征当前迭代策略相较于精炼纳什均衡策略的收益效用偏差,并结合反事实值评价对应个体当前策略下遗憾值最小化指标,使得对应全局博弈的平均整体遗憾值最优.随着深度强化学习技术的发展,神经网络因其较强的拟合能力引入纳什均衡策略求解方法中,神经虚拟自我对弈算法（neural stochastic fictitious play,NSFP）[54]通过建立对应博弈模型中对抗双边的局中人策略空间,训练对应敌方平均策略的最佳响应策略,实现对应博弈模型纳什均衡策略的求解与精炼.在传统强化学习模型的基础上,进一步结合深度神经网络优化强化学习训练架构设计,建立泛化性博弈模型纳什均衡求解框架,是未来多阶段博弈对抗纳什均衡策略求解与精炼的突破方向.

5 结论

本文结合无人机集群反制与对抗的典型任务场景需求与感知决策控制的基本作战流程,从无人机集群系统的群体动力学模型、统计特征模型和博弈对抗模型出发,探讨了集群对抗研究中群体行为演化控制问题、对手建模问题与集群博弈对抗问题的理论基础与关键技术.在此基础上,针对集群对抗过程中战场态势高度动态变化、敌我双方对抗策略信息不完备的特点,分析了动态集群网络拓扑结构即时修复,敌方集群全局状态估计与集群博弈对抗纳什均衡策略求解与精炼的研究难点与挑战,为未来无人机集群系统反制与对抗的研究提供了新的解决思路与借鉴参考.