基于主被动源频散曲线拼接策略的面波频散曲线反演研究

方嵩根，吴荣新，吴海波，2

(1.安徽理工大学 地球与环境学院,安徽 淮南 232001;2.合肥综合性国家科学中心能源研究院(安徽省能源实验室),安徽 合肥 230000)

1 引言

近年来,我国城市化的快速发展促进了城区建设的高速增长,为保障其安全运转,亟需一种安全、高效且无损的地球物理探测技术来进行浅地表地质调查[1-2]。横波速度是浅地表探测领域中的重要参数之一,可通过反演面波相速度频散曲线获得[3]。面波探测方法具有能量大、信噪比高、抗干扰能力强及频散等特点,因此被广泛地应用于浅地表探测,成为一种可靠的探测手段[4-5]。

面波勘探根据震源类型不同可以分为主动源面波法和被动源面波法。1999年,Park等[6-7]提出了面波多道分析方法(Multichannel Analysis of Surface Waves,MASW),此方法充分利用了多道地震记录中的面波信息,从而提高了面波的成像能力、精度及稳定性,也可以较好地分离不同模式的面波能量,大大提高了高频面波方法的适用性。但是主动源方法受震源激发频带的影响,探测深度通常为地下30 m以浅,高能量的炸药震源在城市条件下激发也受到了环境限制,难以实现。随着背景噪声互相关技术(Noise Cross-correlation Function,NCF)的发展,基于背景噪声互相关技术提取格林函数的被动源面波法被逐渐应用在城市地下空间的观测当中,其中以基于地震干涉法的面波多道分析方法(Multichannel Analysis of Passive Surface,MAPS)为主[8-10]。由于MAPS方法是从环境噪声中恢复有用面波信号,克服了主动源方法抗干扰能力差的缺点,同时其探测深度也更大。但被动源方法获得的面波频散能量主要集中在低频段,故其对浅层的分辨能力有限,同时在高频段容易受到体波和空间假频等干扰[11-14]。

为获取更宽频带的频散曲线,国内外专家学者提出诸多主被动源相结合的方式,如频谱叠加,混合源面波等方法[15-19]。本文利用模拟数据分别反演主动源、被动源及拼接频散曲线,对比结果验证拼接策略的有效性。通过意大利Mirandola地区的实测数据进行瑞雷波主动源与被动源频散曲线拼接及反演的应用,利用反演结果对比分析拼接策略对浅地表探测结果的影响,证明了主动源频散曲线拼接能有效地提高反演结果的精确度。

2 多阶频散曲线拼接处理流程

利用拼接策略反演地下结构流程与传统面波勘探流程相近,如图1所示,主要分为数据采集、频散分析提取频散曲线、反演频散曲线,只是在分别提取主动源和被动源频散曲线之后,需要将二者相结合,得到一条新频散曲线。下面介绍具体操作步骤。

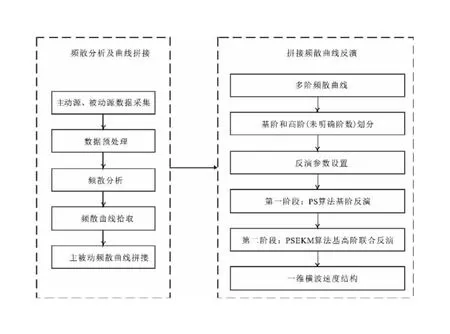
图1 主被动源频散曲线拼接策略处理流程Fig.1 Processing flow chart of active and passive source dispersion curve stitching strategy

2.1 主动源频散分析

对采集到的主动源面波数据进行预处理[20],利用相移法对处理后数据进行频散分析。相移法是由Park等[21]在1998年提出的一种频散分析方法。频散谱计算公式如下所示：

(1)

式中：f为频率,单位Hz;v为相速度,单位：m/s;N为接收道数;j为道号;Rj(f)对应于偏移量为xj的记录在第j道的傅里叶变换频谱。通过扫描一系列实验相速度值,逐道进行求和,即可得到对于频率f的相速度谱E(f,v),显然当实验相速度值等于真实相速度值时,频谱能量图上叠加的能量最强。

2.2 被动源频散分析

利用MAPS法对预处理后的被动源数据进行频散分析,MAPS法是由Cheng等[8]在2016年提出的基于地震干涉(Seismic Interferometry,SI)和路边被动法(Roadside Passive Multichannel Analysis of Surface Waves,PMASW)的混合方法。首先对多道噪声记录进行互相关运算获取虚拟炮集,然后应用相移法对虚拟炮集进行频散分析计算面波频散能量谱。频散结果表达式为：

(2)

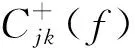
2.3 主被动频散曲线拼接

利用上述方法得到主动源与被动源的频散谱,拾取频散谱上能量团的峰值得到对应频散曲线点。由于两种方法所得频散的有效频带范围不同,对两种方法得到的频散曲线进行拼接,获取频带更宽的频散曲线。为了确保拼接频散曲线的准确性,主被动源的数据采集需要使用同一套观测系统,从而避免由于空间采样率存在差异,降低反演结果的空间分辨率。在此条件下,主被动源频散曲线在频率重叠部分的速度值基本吻合,取其算术平均值,以提高拼接频散曲线质量。若在频率重叠部分的速度值差异较大,可能是因为线性阵列受到局部强震源等噪声源分布不均匀的影响,导致频率重叠部分的被动源相速度偏高,传统频散曲线拼接方法也因此受到限制。对于非均匀噪声源带来的频散测量误差,Liu等[22]提出了被动源面波的伪线性阵列分析方法(Pseudo-Linear-Array Analysis of Passive Surface Waves,PLAS),在线性阵列中增加两个检波器来补偿方位角覆盖,利用聚束分析方法计算噪声源的分布情况,进而获取准确的频散测量结果。Zhang等[23]为解决局部强源问题,提出了局部强源下的被动源面波分析方法(Local-Source Passive Surface Wave Analysis, LSPSW),使用匹配场技术计算噪声源分布,从而提取出可靠的被动源面波相速度。利用上述方法能够得到更加准确的被动源面波频散曲线,进而得到高质量的主被动源拼接频散曲线。

2.4 频散曲线反演

利用嵌入库恩蒙克雷斯算法的模式搜索(The Pattern Search With Embedded Kuhn-Munkres Algorithm,PSEKM)算法对拼接后频散曲线进行反演,该算法是由Yan等于2022年提出的一种多阶模式频散曲线反演方法[24]。该方法将反演过程分为两个阶段：第一阶段采用模式搜索(Pattern Search,PS)来反演基阶频散曲线,以获取一维横波速度;在第二阶段,将第一阶段得到的反演结果设置为初始模型,并将高阶频散曲线添加到反演系统中,采用PSEKM算法来最小化拟合误差。

PSEKM算法利用两步法的反演策略,避免了因初始模型设置不准确带来的反演误差。传统面波反演方法始终需要人工识别高阶模式波的阶数,这是一项耗时且易出错的工作。尤其是在一些特殊介质结构中,例如异常速度夹层带来的模式跳跃,或者多阶瑞雷波常见的模式情况下,识别高阶频散曲线阶数变得更加困难。KM(Kuhn-Munkres)算法的引入,让高阶模式波的阶数识别问题转化成了一个加权二部图的最大匹配问题。在模型更新过程中,利用动态模式对模型阶数进行估计,以便将相速度实测值的模式阶数与当前模型理论值的模式阶数匹配。当拟合误差满足反演要求时,就可以确定高阶模式频散曲线的阶数。

所以利用PSEKM算法进行多阶的主被动源频散曲线联合反演时,只需要将高阶频散曲线数据视作一个集合,无需人工判断其准确阶数。该策略不仅省时,还能避免人工误判导致的反演错误。

3 理论数据测试

为验证主被动源频散曲线拼接策略的准确性,本文使用四层层状介质模型进行测试。四层速度递增的地下介质结构模型参数如表1所示。通过对比主动源、被动源和拼接频散曲线的反演结果,探究频散曲线拼接策略是否能提高模型的重构精度。

表1 四层层状介质模型参数

图2给出了主动源频散曲线、被动源频散曲线和主被动源拼接频散曲线的反演结果。图2(a1)～图2(a3)为主动源频散曲线反演。其中,图2(a1)为实测频散曲线与理论频散曲线之间的拟合情况,从图中可以观察到实测值与理论值拟合良好,其均方根误差仅为2.04 m/s。图2(a2)为反演的横波速度结构与真实模型对比,由于10 Hz以下频带范围内低频信号缺失,导致反演的横波速度模型深度仅有30 m,将反演的前三层与真实模型的第一层对应,平均横波速度与真实值的相对误差仅为0.000 26,此结果说明了主动源面波方法具有浅层分辨率高的优势。图2(a3)为反演模型横波速度与层厚的误差,由于主动源未能反演出30 m以下的地层,所以未给出后两层的误差值。

图2(b1)～图2(b3)被动源频散曲线反演。其中,图2(b1)为仅反演被动源频散曲线的频散曲线拟合情况,均方根误差为2.32 m/s。由于实测值皆处于20 Hz以下的低频段,所以图2(b2)中反演深度达到了80 m,相较于主动源有明显的提升,但是反演结果与真实模型存在较大差异。图2(b3)显示了被动源反演的横波速度和层厚与真实模型间的误差,不难看出,反演结果中第三层横波速度和二、三两层层厚与真实模型差异明显,相对误差值分别为0.145 5、0.246 7和0.207。

图2(c1)～图2(c3)为主被动源拼接频散曲线反演。其中,图2(c1)为拼接频散曲线的拟合情况,均方根误差仅为0.93 m/s,这比主动源和被动源的拟合程度都要更好。图2(c2)显示出拼接频散曲线的反演结果比被动源反演结果更加接近真实模型。从图2(c3)中可以看出,被动源反演差异较大的三个参数相对误差值分别降到了0.095 8、0.176和0.127。说明使用主被动源频散曲线拼接策略进行反演,能够完美地结合主动源方法浅部分辨率高和被动源方法反演深度大的优势,使反演精确性得到进一步的提高。

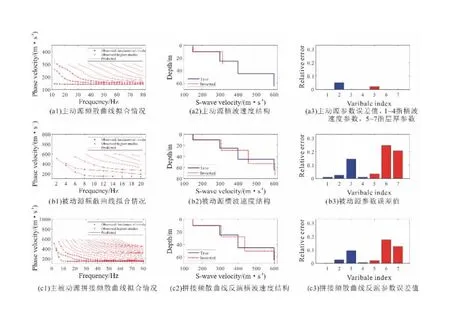
图2 模拟三类频散曲线的反演情况Fig.2 Inversion of dispersion curves of simulated three types

4 实测数据分析

4.1 数据采集

本次试验的主动源和被动源面波数据均来自InterPACIFIC项目中的公开数据集,采样地点设在意大利Mirandola地区。该地区地质结构由含砂层和粉质黏土层的冲积层组成,覆盖在距离地面50～150 m深的中下更新世时期较硬的海相和过渡岩状沉积物之上。数据采集场地平坦,位于住宅区的边界,相对安静。

野外数据采集使用Geometrics公司研制的Geode地震仪,检波器为主频4.5 Hz的垂直分量检波器。其中主动源面波采用24道接收,道间距2 m,震源由8 kg的大锤锤击铁板产生。主动源记录采样时长为2 s,采样间隔为0.25 ms,。被动源面波接收器排列与主动源相同,背景噪声采集时长为524 s,采样间隔为8 ms。

4.2 频散曲线提取和拼接

对主动源数据进行预处理后,使用相移法进行频散分析,分析结果如图3(a)所示。得到频率范围为0～25 Hz、相速度范围为50～550 m/s的频散谱。处理被动源数据时,首先将地震记录分割为一系列时长为5 s的片段,然后对数据片段进行去均值、去趋势、时间域归一化等处理。对预处理后的各数据片段进行互相关计算,并进行叠加获取虚拟炮集,使用相移法对虚拟炮集进行频散分析,得到频率范围为0～20 Hz、相速度范围为100～500 m/s的频散谱(图3b)。

从图3(a)中可以观察到,主动源数据小于25 Hz频带范围内的基阶频散能量连续且集中,20 Hz之后的高阶模式频散能量比较收敛,但阶数很难人工判断。图3(b)表明了被动源数据的频散能量在1～20 Hz低频范围内十分发育,可以明显观察到有三种以上不同阶数的频散能量带。

如图3(c)所示,将被动源频散曲线与主动源频散曲线拼接,可以获得频带更宽的频散曲线。主动源与被动源的基阶频散曲线在5～8 Hz重叠频段内相速度值相同。第一高阶频散曲线形态趋势一致。

图3 频散曲线示意图Fig.3 Schematic diagram of dispersion curve

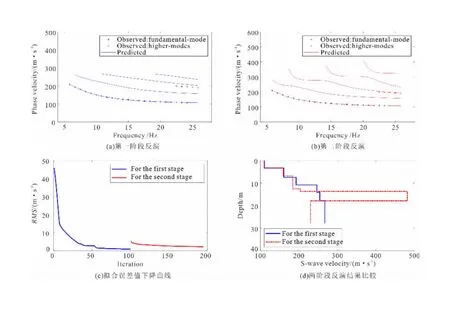
图4 主动源频散曲线反演结果Fig.4 Inversion results of dispersion curve of active source

4.3 地下速度结构的反演

根据4.2节拾取出的主动源频散曲线和主动源与被动源的组合得到的频散曲线,采用PESKM算法对频散曲线进行反演。设置了一个每层厚度相等,最后一层为半空间的六层模型为初始模型。

单独反演主动源频散曲线时,反演结果如图4所示。由图4(a)可以看出,在第一阶段仅反演基阶频散曲线时,反演结果与手动拾取的基阶频散曲线拟合较好,与高阶频散曲线的拟合程度较差。图4(b)显示,第二阶段反演在引入高阶频散曲线之后,反演出来的频散曲线与高阶频散曲线更加拟合,拾取到的高阶频散曲线由KM算法匹配到了第二高阶。从图4(c)中可以看出,第二阶段初始的拟合误差值大于第一阶段结束时的拟合误差值,说明在高阶相速度频散曲线中包含更多的模型约束信息,经过了两阶段反演,拟合误差进一步降低。从反演结果图4(d)可以看出,主动源数据的地层探测深度最深接近30 m,对于浅部地层有着较高的分辨率。仅反演基阶频散曲线时,横波速度呈现一种随着深度的增加而逐渐变大的趋势,而二阶段反演结果则显示在地下14～18 m处有一处高速夹层,横波速度达到了480 m/s,18 m以下介质的横波速度又降低至230 m/s。

为结合两种方法的优势,将主动源和被动源提取出的频散曲线进行拼接,反演拼接后频散曲线的结果如图5所示。与主动源反演结果类似,仅反演基阶频散曲线时,与高阶频散曲线拟合程度较差,但是反演深度能够达到80 m,是仅反演主动源频散曲线结果的两倍,第二阶段引入高阶模式频散曲线后,反演同样提高了高阶频散曲线拟合程度。与主动源反演结果不同的是,属于主动源数据的高阶相速度值由KM算法匹配到了第一高阶。分析是由于主动源的高阶模式能量不发育,低质量的高阶信息参与到未定阶数的PSEKM反演过程中,不仅无法约束反演,反而会使反演结果病态化。而被动源数据的加入补充了高阶模式数据,稳定了反演过程,并提高了横波速度的分辨率。从横波速度结构反演结果来看,拼接频散曲线反演的深度同样能达到80 m,并且反演结果与基阶频散曲线结果相比,准确性得到了进一步的提高。

5 结论

本研究提出了一种主被动源频散曲线拼接策略,对主动源和被动源多阶频散曲线进行拼接,得到频带更宽、信号更丰富的频散曲线,拼接后频散曲线能够反演出更加准确的横波速度模型。利用数值模拟和实测数据应用此策略进行频散曲线反演,结果表明了反演拼接频散曲线能结合主动源方法与被动源方法的优势,在保证地下介质高分辨率的前提下提高了探测深度。反演结果验证了主被动源拼接频散曲线反演策略的准确性和有效性,为解决实际工程中的地震勘探问题提供了重要手段。

致谢

感谢InterPACIFIC项目提供的实测数据;感谢南方科技大学闫英伟博士公开的反演算法SWPVPSEKMInv。