非齐次边界条件Rosenau-KdV 方程的有限差分格式
刘佳垚,王晓峰,罗诗栋
(闽南师范大学 数学与统计学院,福建 漳州 363000)
0 引言
非线性波现象的研究是非线性研究中的一个重要课题,而非齐次边界问题一直是非线性波动问题研究中的一个难点.对于非齐次边界的处理有很多方法.Passonen V I[1]提出了由相邻网格单元(包括边界单元)组成的平衡单元和不使用方程本身的情况下近似边界条件这两种处理边界条件的方法.Chen A 等人[2]将微分方程的定性理论应用于渗透分散的K(2,2)方程,得到了渗透K(2,2)方程在非齐次边界条件下的光滑、峰值和锥孤波解.除了上述方法,有限差分法也可应用于非齐次边界条件的处理.Esser H 等人[3]针对一类非齐次热方程的初边值问题,研究了分别用Crank-Nicolson 差分格式和Saulyev 差分格式求得的近似解的误差界的锐度.Wang X 等人[4]给出了求解边界处具有时间周期的KdV 方程的有限差分格式,并验证了在时间和空间上分别达到二阶和四阶精度.邓等人[5]将非齐次边界KdV 方程转化为齐次边界,并利用有限差分法构造一个三层线性有限差分格式.对于非齐次边界条件Rosenau 方程,Özer S[7]提出了一种基于配置有限元方法的数值法,使用五次B 样条函数来获得由初始条件和边界条件规定的非齐次Rosenau 型方程的近似解.
本文考虑将有限差分法应用到非齐次边界Rosenau-KdV方程:
其中:a1(t),a2(t),b1(t)和b2(t)是关于时间t的函数;u0(x)是已知光滑函数.
1 辅助函数的引入与差分格式的构造
引入辅助函数
其中,θ1(t),θ2(t),θ3(t),θ4(t)是四个待定的未知函数,且满足v(x,t)=0.由(3)—(5)式可以得到以下关于θ1(t),θ2(t),θ3(t),θ4(t)的方程组:
可以求得方程组解为
其中,L=xr-xl.
将(5)式代入(1)—(4)式中,有
其中:
对问题(6)—(8)考虑以下三层线性有限差分格式:
2 数值解的存在唯一性
引理1[8]对于任意网格函数vn∈,有
定理1差分格式(9)—(11)存在唯一解.
证明设
由初始条件可得存在唯一解v0.假设v0,v1,…,vn是唯一解,则考虑格式关于vn+1的齐次方程
将式(12)两端与vn+1作内积,根据引理1 得
由于
故有
取τ足够小,使得
则‖vn+1‖=0,即(12)只有零解.
3 差分格式的无条件稳定性
定理2差分格式(9)—(11)是无条件稳定的.
证明取f(xj,tn)=0,考虑如下齐次方程
故可得|ε| ≤1,因此差分格式(9)—(11)满足无条件稳定性.
4 数值实验
下面我们通过两个数值实验来证明所构造格式的可行性,验证Rosenau-KdV 方程的齐次边界下误差和收敛精度以及Rosenau 方程在不同非齐次边界条件下的图像.
4.1 实验一——Rosenau-KdV 方程
取参数λkdv=1,我们可以得到方程
其初值条件为
精确解为
我们定义误差范数和收敛阶为
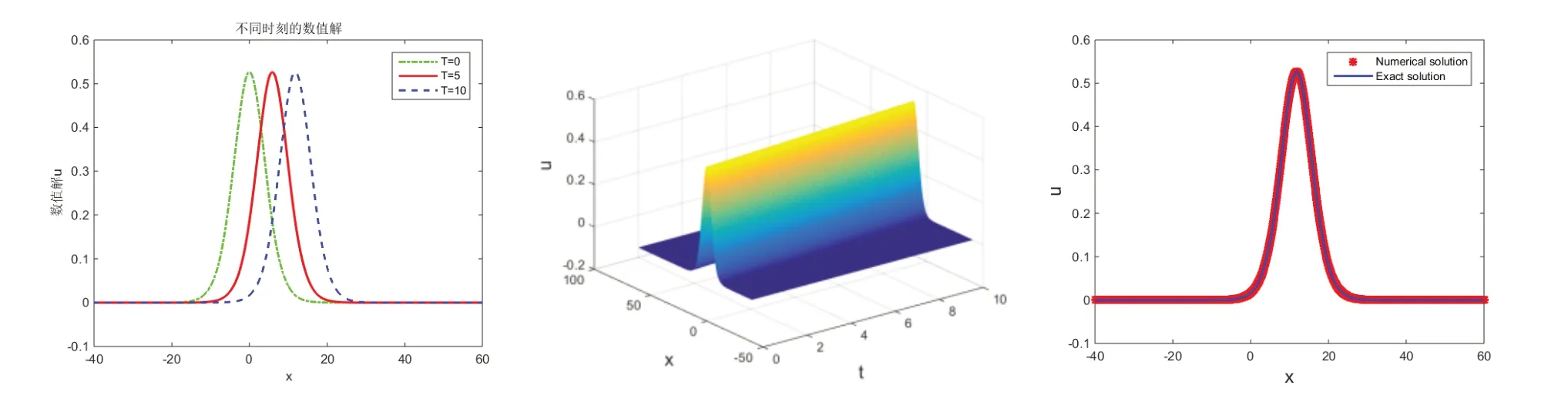
图1 在T=10,τ= h=0.0625时不同时刻的数值解图像

表1 在T=10时不同步长下误差和收敛阶
4.2 实验二——Rosenau 方程
取参数λkdv=0,我们可以得到方程
我们无法得出方程(20)的精确解,因此,取xl=0,xr=3,u0(x)=0,τ=h=0.01,T=3 来 模拟出不同边界条件下的数值解.其中图2采用的是周期函数sin(5πt)来模拟出不同周期边界下的数值解;类似的,图3 采用两个周期函数sin(5πt)和cos(5πt)来模拟数值解.
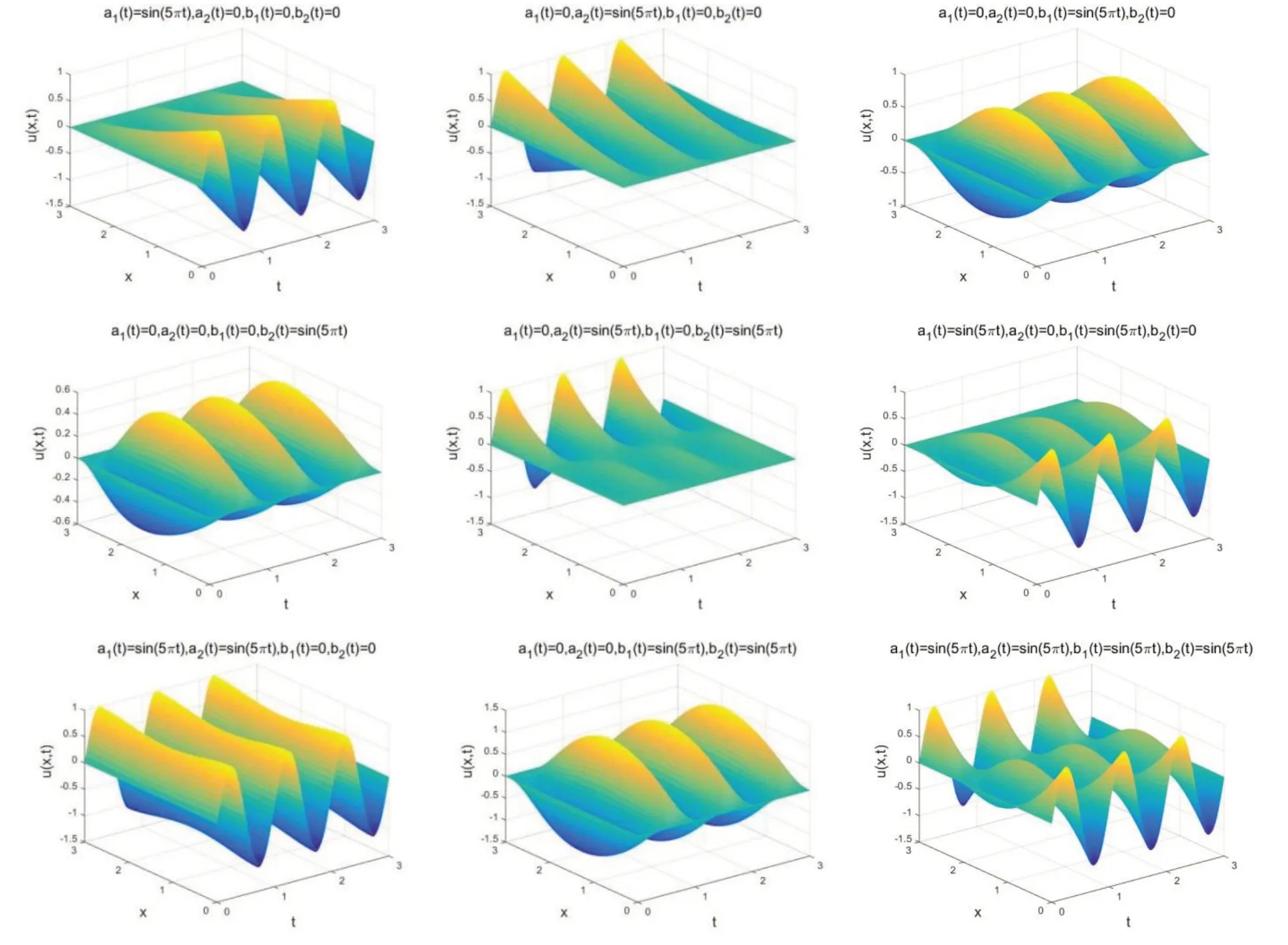
图2 采用周期函数sin(5πt)模拟不同周期边界下的数值解
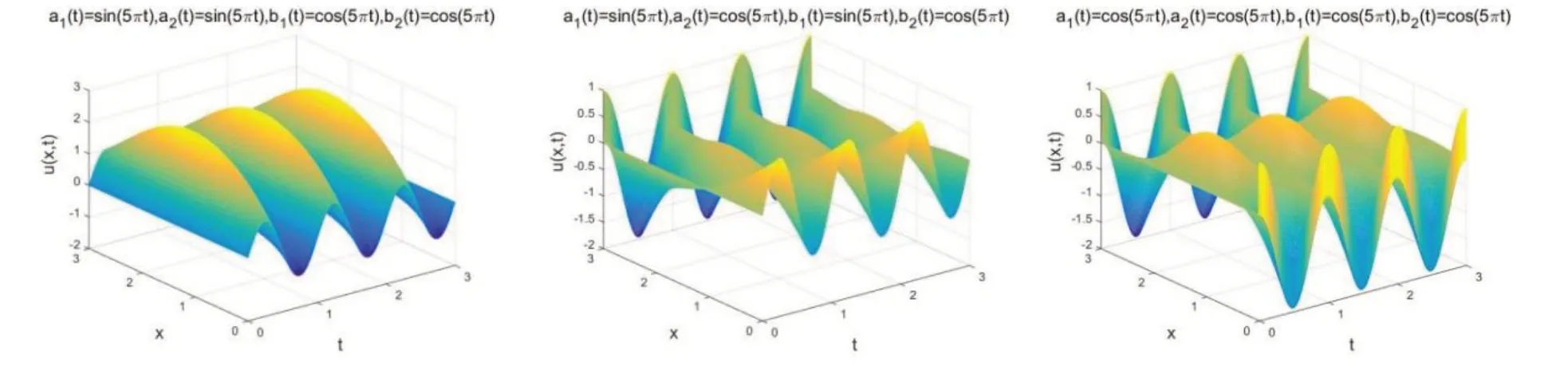
图3 采用两个周期函数sin(5πt)和cos(5πt)模拟不同周期边界下的数值解
从图2 和图3 中可以看出,数值解表现出的周期行为与边界的周期行为相同.

