蜂巢晶格材料中的扩展s 波超导电性

于贤丰，张李婷，蓝 郁

（衡阳师范学院物理与电子工程学院，湖南衡阳 421002）

0 引言

蜂巢晶格材料的非常规超导电性[1]自二维材料石墨烯被发现以来就逐渐引起学者们对其的研究兴趣.实验结果表明，蜂巢晶格材料In3Cu2VO9在半满时是反铁磁绝缘体[2].而Hubbard模型的理论研究也证明[3,4]，蜂巢晶格材料半满时在足够大的U 的情况下表现为反铁磁莫特绝缘体，这与铜氧化物高温超导体的母体化合物很相似[5]，后者通过掺杂引入载流子后就能产生非常规超导现象.两者在半满时的相似性使人们认为掺杂的蜂巢晶格材料应该也能出现超导态，其实这也是蜂巢晶格材料的超导电性备受关注的原因之一.实验结果也证实，两个单层错开一个约1.1°小角度的双层石墨烯（被称为魔角石墨烯）在半满时表现为反铁磁莫特绝缘体[6]，引入载流子偏离半满后则出现了非常规超导电性[7].

常规超导体中库珀对的两个电子是通过电子-声子相互作用而吸引在一起的[8]，但是对于铜氧化物这样的高温超导体来说电子-声子相互作用不足以驱动电子形成库珀对，其超导机理不能为传统的Barden-Cooper-Schrieffer (BCS)理论[8]所解释，所以被称为非常规超导体.对于非常规超导电性的研究，超导态的配对对称性是非常重要的问题.到目前为止，相当多理论认为蜂巢晶格材料的超导态主要是d+id波配对对称性的[9-17]，但也不乏理论支持其他配对对称性，例如p+ip波[18,19]、f波[20,21]、扩展s波[22]等.关于蜂巢晶格材料的超导电性目前还处于激烈的争论之中，离取得一致的结论还有很长的路要走，因此仍需继续进行深入的研究，以获得一致的认识.另外，研究蜂巢晶格掺杂莫特绝缘体本身也能揭示新奇的量子相，使实现奇异的超导电性成为可能.

在研究铜氧化物超导电性的过程中，冯等发展了一套动能驱动的超电性理论[23,24]，获得了与实验结果定性一致的理论结果，解释了铜氧化物超导体超导态的性质.鉴于半满时的蜂巢晶格材料也表现为反铁磁莫特绝缘体，本文将利用这套动能驱动的超导电性理论[23,24]来研究蜂巢晶格材料的非常规超导电性.

1 理论框架

t-J模型被认为可以有效描述掺杂莫特绝缘体的低能物理行为[24-27]，而蜂巢晶格为双子格子的复式晶格，其t-J模型可以写成

为了研究掺杂蜂巢晶格材料的超导电性，需要进行超出平均场近似.根据Eliashberg 强耦合理论[31]，全电荷载流子正常和反常格林函数满足以下方程组：

其中，电荷载流子正常和反常格林函数均为矩阵

粒子-空穴通道和粒子-粒子通道的自能函数分别为

其中，gAA(k,ω)=gBB(k,ω)，我们只考虑最近邻格点之间的电荷载流子配对态，故已将反常格林函数和粒子-粒子通道的自能函数的对角项设为零.

其中：ν=1,2 分别表示成键态和反键态；

这里的θk是的辐角，Z=3 表示最近邻格点数.粒子-粒子通道的自能则包含了电荷载流子配对力和配对能隙参数的信息，定义电荷载流子配对能隙为

经过以上处理，我们求得全电荷载流子正常和反常格林函数分别为

这里：

为准粒子相干因子，满足归一化约束条件

利用平均场近似的自旋格林函数和全电荷载流子格林函数式（4）、（5）和（6），求得电荷载流子准粒子相干权重和配对能隙参数满足以下方程：

其中,

函数

这里nF(ω) 和nB(ω) 分别为费米和玻色分布函数，的表达式可参见文献[30].

2 结果与讨论

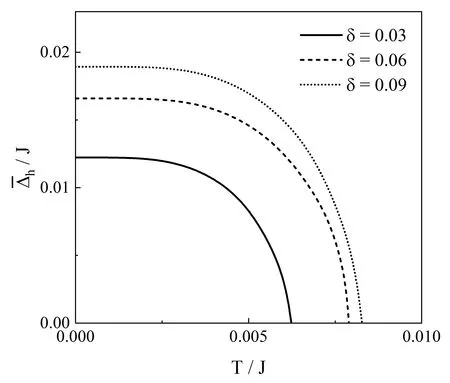
图2 t/J=1.0时电荷载流子配对能隙参数随温度的变化

为了对超导转变温度Tc有更清晰的认识，我们在图3 给出了超导转变温度随掺杂浓度的变化，即相图.显然，超导转变温度随掺杂浓度的变化曲线和电荷载流子配对能隙参数的相似，也呈圆顶状.当蜂巢晶格偏离半满时，超导转变温度随掺杂浓度的增加而升高，在掺杂浓度d=0.09 附近达极大值，然后超导转变温度随掺杂浓度的增加而逐渐降低，这与魔角石墨烯的实验结果[7]定性一致.超导转变温度随掺杂浓度的变化呈圆顶状的结果说明在中等浓度区域实现超导较易一些，在较高的温度下即可使材料变为超导态，而低掺杂浓度和较高掺杂浓度区域为实现超导需要将材料冷却到更低的温度.应该指出，超导转变温度与电荷载流子配对能隙参数并非在同一个掺杂浓度下达极大值，这一点与铜氧化物超导体的d波超导态的结果[24]不太相同.

图3 t/J=1.0 时超导转变温度随掺杂浓度的变化

从结果看来，动能驱动的超导电性理论[23,24]是适用于研究掺杂蜂巢晶格材料的非常规超导电性的.该理论指出，反铁磁涨落或者自旋激发与超导电性有直接的关联，源于t-J模型动能项的电荷载流子和自旋之间的相互作用相当强，则可以通过交换自旋激发的方式诱导出电荷载流子配对态进而是电子配对态，从而形成超导电性.蜂巢晶格材料在半满时具有反铁磁性[2-4]，虽然掺杂会破坏这种反铁磁长程序，但是应该与铜氧化物超导体一样偏离半满时仍然存在反铁磁短程关联，即存在自旋激发，自旋激发作为电荷载流子配对的媒介使得掺杂蜂巢晶格材料中可以出现非常规超导电性，而我们的计算结果则证明了这个结论.本文的研究结果也进一步表明动能驱动的超导电性理论适合研究低维掺杂莫特绝缘体的非常规超导电性.

3 结论

本文从蜂巢晶格材料的t/J模型出发，利用动能驱动的超导电性理论研究了掺杂蜂巢晶格材料的扩展s波非常规超导电性.计算结果表明，当蜂巢晶格材料通过掺杂偏离半满后，扩展s波对称性的电荷载流子配对能隙参数随掺杂浓度的变化呈圆顶状，说明蜂巢晶格材料中出现扩展s波超导态是可能的.电荷载流子配对能隙参数在低掺杂浓度区域随掺杂浓度的增加而增加，并在某掺杂浓度处达极大值，然后随掺杂浓度的增加而减小.另外，电荷载流子配对能隙参数随温度的升高而逐渐降低，在超导转变温度处变为零.而超导转变温度随掺杂浓度的变化和电荷载流子配对能隙参数的一样也呈圆顶状.计算结果与铜氧化物超导体的d波超导电性相似，说明动能驱动的超导电性理论是适用于研究掺杂蜂巢晶格材料的非常规超导电性的.