数据增强的自适应权重稀疏子空间聚类算法

江雨燕，陶承凤，李 平

（1.安徽工业大学 管理科学与工程学院，安徽 马鞍山 243002；2.复杂系统多学科管理与控制 安徽普通高校重点实验室，安徽 马鞍山 243002；3.南京邮电大学 计算机学院，江苏 南京 210023）

0 引言

聚类根据内在相似性对数据进行分组的过程。在实际应用领域中，数据具有高维性、复杂性，但是高维数据并不是均匀分布在所有维度空间，而是集中在某些低维结构中，可理解为若干个低维子空间的并集上。子空间聚类方法[1,2]能够将源于不同子空间的高维数据映射至相应的潜在子空间，在图像聚类、模式识别以及生物医药等多研究领域受到广泛关注。

子空间聚类方法主要分为四种：（1）基于迭代的方法[3]，（2）基于统计的方法[4]，（3）基于代数的方法[4]，（4）基于谱聚类的方法[5]。最具影响力的子空间聚类方法利用数据构建邻接矩阵，将谱聚类方法应用于邻接矩阵，得到聚类结果。因此，谱聚类成为子空间聚类方法的主流，而该方法的难点在于如何构建一个好的邻域矩阵。具有代表性的方法包括：稀疏子空间聚类(Sparse Subspace Clustering，SSC)[6,7]、基于低秩表示的子空间聚类(Subspace Clustering based on Low-rank Representation,LRR)[8]，它们之间的区别在于对邻接矩阵的正则化方法不同。另外，结构化稀疏子空间聚类(Structured Sparse Subspace Clustering)[9]通过一种结构正则化方法来量化邻接矩阵和分割矩阵之间的差异，从而将邻接矩阵和子空间聚类两个模块相结合。文献[10]采用邻接矩阵的学习和聚类步骤共同进行的方法，将原始数据的空间信息纳入考虑范围。文献[11]加入了运用判别信息的迁移学习，使之在特征域中与稀疏子空间聚类同时进行。文献[12]提出了基于核理论的非线性拓展的方法。

但是原始数据中往往存在噪声和其他干扰，直接对原始数据进行自表示得到的邻域矩阵也受到噪声或干扰的影响，不一定能反映数据的真实子空间隶属关系，导致数据误分类在网络训练过程中，两个簇边界附近的样本可能不能被准确地分配到集群中心，这可能会混淆甚至误导网络的训练过程，导致泛化性能下降。针对以上问题，本文提出数据增强的自适应权重稀疏子空间聚类模型(Self-Weighted Sparse Subspace Clustering based on Data Augmentation,SWSSC-DA)，该方法的创新主要包括：

（1）使用数据增强技术对原始数据进行随机剪切、旋转、翻转和扭曲等方式进行变换获取更多的样本，此方法仅提前引入先验知识，以适当的方式转换图像，但不会改变其身份。

（2）采用自适应权重学习，给每个样本赋予不同的特征权重，每次倾向于选择“简单”（靠近聚类中心）的样本作为训练集，并逐步添加“较难”（边界附近）的样本。自适应权重学习的变量不存在超参数，并且总是保留边界样本。

1 相关理论

1.1 稀疏子空间聚类模型

稀疏子空间聚类[13]模型如图1 所示，该模型是基于稀疏表示理论，利用一个数据样本和所有样本间的邻域关系作为新特征来学习其自表示系数，通过自表示系数矩阵进一步构建相似度矩阵，最后借助谱聚类方法得到聚类结果。稀疏表示的目的是用尽量少的原子基来表示数据，这种方法对解决全局优化问题具有重要作用。

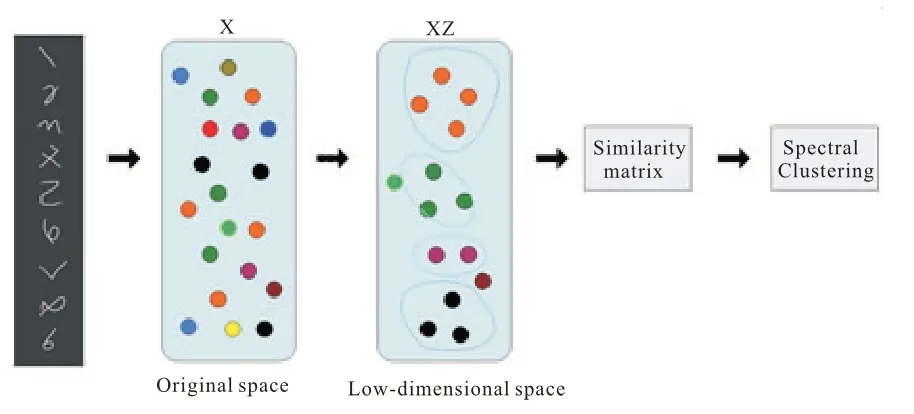
图1 稀疏子空间聚类模型

为了求解最稀疏的zi值，最小化目标函数为：

式(2)中ℓ0范数是指非零元素的个数，考虑数据的高维度特征，求解ℓ0范数是NP-Hard 问题，因此使用ℓ1范数来凸松弛ℓ0范数，将式(2)改写为：

矩阵形式的公式为：

考虑噪声和离群值，式(4)可改写为：

其中λ1、λ2是平衡参数，用于平衡目标函数；C∈ℝD×N表示离群点；E∈ℝD×N表示噪声，‖·‖表示Frobenius 范数。

利用式(5)中的等式约束，消除E：

令Y=|C|+|C|T，其中Y为数据的相似度矩阵，将Y输入谱聚类算法，获得最终聚类结果。

1.2 自适应权重学习

自权重学习[14,15]模拟了人类的学习过程：从简单到复杂。例如，给出一些新任务的样本时，算法在每次迭代过程中首先倾向于选择简单样本进行学习，逐渐选择复杂样本。规定具有较小损失的样本为简单样本，具有较大损失的样本为复杂样本。自权重学习算法经过选择样本、调整模型的过程，在调整完模型后，再次选择损失相对较小的样本，并调整模型，不断进行这样的迭代。因此，在自权重学习中样本的选择并不是随机的，也不是在一次迭代中全部纳入训练过程中，而是通过一种由简到难的方式进行选择。

给出学习模型f，其学习参数为v，并将D={(x1,y1),(x2,y2),(x3,y3),…,(xn,yn)} 作为训练样本，则传统的机器学习目标可表示为：

而自权重学习的目标：

其中W=[w1,w2,…,wn]T为各个样本的权重，g(λ,W)被称作自权重正则化项，λ 作为衡量损失函数“简单性”的标准。λ 和W通过交替搜索策略(ASS)进行优化。对于简单的自权重学习，有g(λ,W)=-λW,W∈[0,1]。即：

给定样本权值W，v上的最小化是一个加权损失最小化问题。当模型参数v固定时，最佳W具有如下闭式解：

自权重学习算法中λ 通常被设置为开始时损失的中位数，然后每隔几次迭代增加步长δ。由于在训练过程中，样本的损失也在减少，因此步长δ难以选择。基于以上分析，模型根据训练过程中损失的统计数据进行设置：

其中Lt表示第t次迭代中的所有损失，μ(*)和σ(*)为损失的平均值和标准差，T为最大迭代次数，由学习模型决定，不是一个独立的超参数。图2(a)显示了传统算法选择样本的情景，图2(b)显示了在开始时使用虚线圈中的样本进行迭代更新，即自适应权重选择样本的情景。

图2 选择样本迭代更新的过程

1.3 数据增强技术

深度神经网络很容易导致数据过拟合，这一问题可以通过获取更多的训练数据、限制深度神经网络的能力或提前停止来解决。而数据增强是扩展训练数据集的一种有效方法，对于一个给定的图像样本，在将它输入网络之前，通过随机旋转、移位、剪切及扭曲等方式进行变换获取更多的样本，如图3 所示。数据增强技术提前引入先验知识，以适当的方式转换图像但不会改变其身份。数据增强技术现已在监督模型中应用，但是在无监督聚类分析中被忽视[16]。

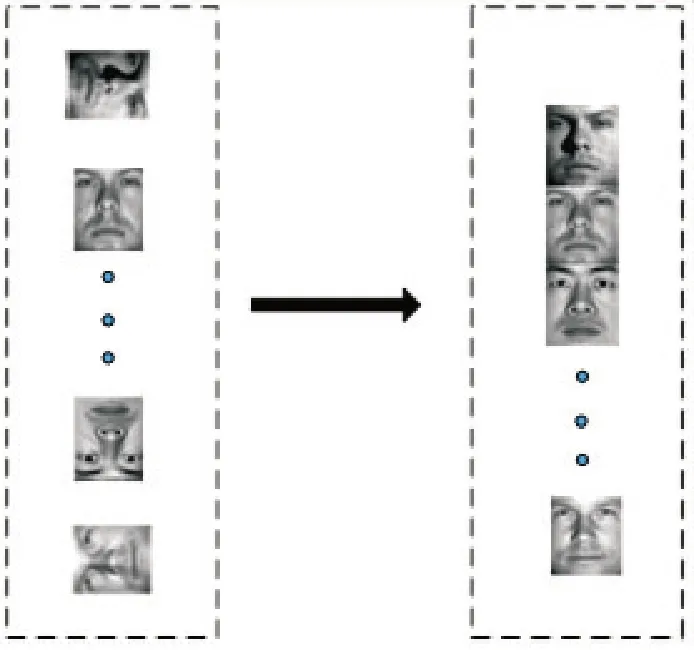
图3 数据增强技术

2 数据增强的自适应权重稀疏子空间聚类

2.1 提出的模型

在深度神经网络训练过程中，数据增强技术通过随机旋转、移动、裁剪、剪切等方式进行图像变换，扩展了训练数据集，解决了数据的过拟合问题。受其启发，本文提出在稀疏子空间聚类模型进行稀疏表示之前，对原数据进行数据增强处理，以适当的方式转换图像，但并不会改变数据本身。

由于稀疏子空间聚类模型在迭代过程中，总是随机选择样本进行训练，并没有考虑两个簇边界的样本会误导训练效果。本文提出使用自适应权重学习对每个样本赋予不同的权重，由“简单”（靠近聚类中心）样本到“较难”（边界附近）样本的先后顺序进行迭代。求出优化解、获得邻域矩阵，将其进行谱聚类，数据增强的自适应权重稀疏子空间聚类模型如图4 所示。

图4 数据增强的自适应权重稀疏子空间聚类模型

为了使模型更具鲁棒性，提出对原样本xi∈X(X∈ℝD×N)设置不同的权重，每次迭代选择最具说服力的样本，特别地，这种自适应权重学习的方式不会改变数据的结构信息。因此，式(6)可以改写为：

定义映射Λ 表示数据增强函数，可以是任意旋转、移位、剪切、扭曲等的组合，数据增强后的样本表示为=Λ(X),X∈[x1,x2,…,xn]T。将上式中的原样本X替换为增强样本，式(12)改写为：

实际上，数据位于放射子空间而非线性子空间的并集。为了将位于仿射子空间并集中的数据点进行聚类，稀疏子空间方程可优化为：

引入辅助变量A∈ℝN×N，加入参数λ3和2 个惩罚因子：

引入拉格朗日乘子δ∈ℝN，Δ ∈ℝN×N得到数据增强的自适应权重稀疏子空间聚类算法的目标函数：

其中，λ 由（11）计算，上式的优化解通过交替方向乘子法计算；令S=|C|+|C|T，其中C为稀疏表示矩阵，S为数据的相似度矩阵，最终使用谱聚类方法得到聚类结果。

表1 参数符号说明

2.2 算法优化

1.固定Z,C,W,δ,Δ，通过更新A极小化L：

其中，λ 由（11）计算。

2.3 时间复杂度

本文算法中更新变量A,C,W,δ,Δ 的计算复杂度均为O(n2)，更新邻域关系矩阵需要求解Sylvester 方程，则计算复杂度为O(n3)，因此算法的总计算复杂度为T×O(n3)，其中T 为迭代次数。

3 实验设置及结果分析

本文的实验环境为Microsoft Windows 10，处理器为英特尔酷睿i7，内存容量8 GB，显卡配置为MVIDIA GeForce 920 M。模型在同一数据集进行5 次独立实验，取平均值作为最终实验结果。

3.1 数据集

模型在常见数据集上进行大量实验，以验证所提算法的有效性，数据集包括：MNIST[17]、USPS[18]、ORL[19]数据集，图5 展示了这些数据集中的部分图像。

图5 部分样本图片

（1）MNIST 数据集：由训练集中60 000 个样本和测试集中10 000 个样本组成。本文取训练集每类手写字的前100 幅图像来进行了实验，将图像大小调整为28×28。

（2）USPS 数据集：含有11 000 张图像，是由“0”-“9”共10 个手写数字的类组成。本文使用每个手写数字的前100 张图像的子集进行实验，将图像大小调整为16×16。

（3）ORL 数据集：有40 名受试者，每名受试者有10 个样本，则人脸图像共计400 张。每名受试者图像在不同的光照条件下拍摄，带有不同的面部表情(睁眼/闭眼、微笑/不微笑)或面部饰品(有/无眼镜)，将图像大小调整为32×32。

3.2 评价指标

为了评估聚类算法的性能，本文采用了准确度（ACC）评价指标，ACC 的值越大，聚类性能就越好。

ACC 被定义为：

其中yi是标签，ci是模型的聚类分配，m(·)是聚类分配和标签之间的映射函数，1(·)是指示器函数返回1 或0。

3.3 与其他方法的对比分析

本文将该方法与以下几种方法在上述数据集上进行了比较，其包括：SSC、LRR、LSR、SSSC、SRR。

稀疏子空间聚类(Sparse Subspace Clustering,SSC)：利用稀疏线性组合特征表示数据点之间的关系，并构造子空间近邻矩阵。

低秩表示(Low Rank Representation,LRR)：此方法的邻域矩阵是通过对数据施加低秩约束来获取，从而捕获数据的全局结构。

最小二乘回归(Least Squares Regression,LSR)[20]：对自表示系数采用范数正则化，具有将高度相关的数据聚集在一起的优点，但也会导致类内类间的自表示都是均匀的，不利于分离不同类别数据。

结构化稀疏子空间聚类(Structured sparse subspace clustering,SSSC)：利用结构化稀疏线性组合特征表示数据点之间的关系，同时引入联合正则化项实现系数矩阵和聚类标签的联合学习，使得模型直接输出得到聚类标签。

基于结构化稀疏关系表示的子空间聚类(Subspace clustering via structured sparse relation representation,SRR)[21]：首先对原始数据进行自表示得到邻域关系矩阵，反映了每个数据与其它数据的某种相关性；然后将每个数据的自表示向量作为数据的新特征，对其再进行二阶自表示得到重构系数矩阵，由此矩阵构造相似度，并用谱聚类得到最终聚类结果。

将本文算法与上述几种算法结果汇总，如表2-3 所示。为确保实验的公平性，上述算法实验均由作者提供的代码进行，具体参数根据论文设置为最优。

表2 不同算法在MNIST、USPS、ORL 数据集上聚类准确度(%)对比

由表2 可知，在3 个公开数据集上，本算法精确度相比其他子空间聚类算法均得到一定的提高。相比最优算法SRR，在数据集MNIST 上精确度提升了3.77%、在USPS 上精确度提升了4.30%、在ORL 上精确度提升了2.45%。这说明模型使用随机位移和旋转对原样本进行数据增强，通过交替地使用增强样本来训练和优化自编码器，并更新样本的集群分配，能够学习到稳健的特征；并且，为了稳定网络训练，利用无需额外超参数的自适应自步学习，在每次迭代中选择最具说服力的样本能够较好地提高泛化能力。

将所有模型在3 个数据集中指定数据上的运行时间进行对比，由表3 可知，算法LSR 的运行时间最少。运行时间长短与算法的计算复杂度有关，本文算法与SRR 算法同为3 阶计算复杂度，但本文算法的实际运行时间少于SRR，说明在运行时间上有一定的提升。

表3 不同算法在MNIST 训练集每个数字前100 幅图片、USPS 训练集每个数字前100 幅图片、ORL 的40 个对象的运行时间（秒）对比

3.4 SWSSC-DA 不同部分的结果分析

在实验中，通过消融实验分析本文提出的数据增强(DA)和自适应权重学习(SW)两个部分的贡献，从SWSSC-DA 中删除DA 意味着在（16）中用替换。在SWSSC-DA 中禁用SW 对应于在（16）中固定W=1。移除所有这三个部分的配置视为稀疏子空间聚类(SSC)。

表4 显示了不同配置下的SWSSC-DA 的结果，分别将DA、SW 之一添加到SSC 中时，性能在大多数情况下都会有所提高。由表4 可以得出：在SSC 算法中单独加入DA 比单独加入SW 的精确度更高，这是因为数据增强技术通过随机位移和旋转对原数据集进行扩充，获得了更多的样本数据图像。虽然在USPS 数据集上单独加入DA或SW 的效果并不是特别的出众，但是两个一起加入时也有提升。通过引入所有这三个部分，SWSSC-DA 成功地在所有数据集上实现了最好的性能。

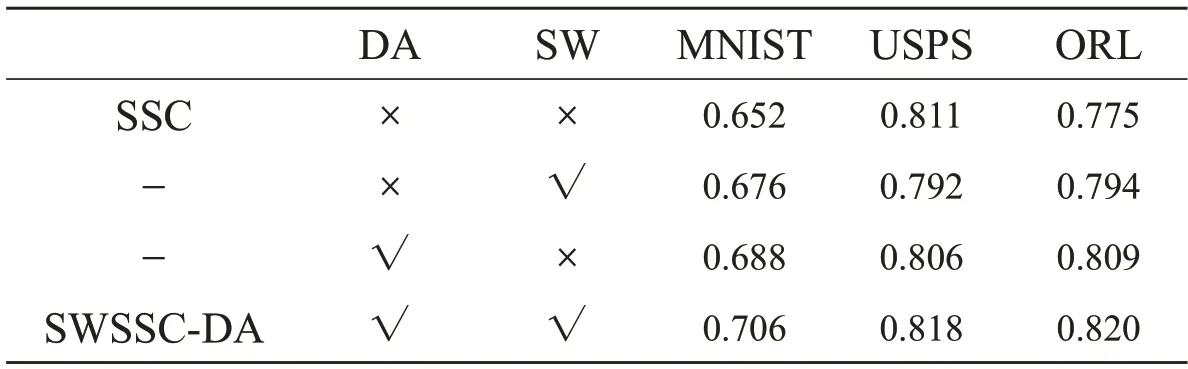
表4 不同配置下的SWSSC-DA 的结果对比

3.5 超参数灵敏度分析

在涉及深度神经网络时，存在一些无法避免的超参数，本文研究了超参数在数据增强中的敏感性。在实验中，只使用随机旋转和移位。采用0o,10o,...,60o进行旋转，采用0,1,...,6 像素进行移位转换，在每个得到的49 个网格上运行SWSSCDA 算法两次，并取平均结果。由于过多信息的丢失会导致模型的性能急剧下降，如图6 所示，在MNIST 数据集上旋转[0o,30o]和移动[0,3]像素的范围内，在USPS 数据集上旋转[0o,40o]和移动[0,4]像素的范围内，在ORL 数据集上旋转[0o,40o]和移动[1,4]像素的范围内，该模型的性能较稳定，总体来说，本文提出的算法对大范围内的数据增强所引入的超参数不敏感。

图6 随机旋转和移位在数据增强中的敏感性

4 结束语

本文提出了数据增强的自适应权重稀疏子空间聚类模型（SWSSC-DA）来学习鲁棒的面向聚类特征。模型在网络训练中通过自适应权重学习优先选择易分类的样本，将集群边界附近的样本排除在训练之外，避免难分类样本产生误导性的记忆。将数据增强技术引入稀疏子空间聚类，通过随机旋转和移位扩充数据样本。模型在三个公开数据集上进行实验，获得了比传统聚类算法更好的聚类效果，提高了聚类精确度。通过消融实验、超参敏感度和收敛性分析等加强验证了本文所提算法的有效性。将对抗性学习方法引入子空间聚类，生成对抗自编码器能更加精准地对样本进行聚类分配并提高聚类精度是下一步研究的方向。