基于Gibbs 抽样算法的两参数Pareto分布的Bayes 估计

李凡群，韦善然

（安徽财经大学 统计与应用数学学院，安徽 蚌埠 233000）

Pareto 分布是由意大利经济学家Pareto V 提出的收入分配理论中一个重要的分布[1]，在各个领域都被人们广泛应用，例如城市人口容量、股票价格的波动、商业、保险等模型等都可以用Pareto 分布来进行描述，因此，研究Pareto 分布的统计性质是具有现实意义的。刘芹等[2]给出了不同损失函数下Pareto 分布参数的Bayes 估计；韩明［3］给出了Pareto 分布在尺度参数已知时，平方损失下形状参数的E-Bayes 估计和多层Bayes 估计；朱宁［4］研究了复合MLINEX 损失函数下Pareto 分布参数的Bayes 估计，并证明了其是可容许的；杨冬霞等[5]讨论了复合Mlinex 损失函数下指数威布尔分布参数的Bayes 估计；刘飞等[6]讨论了基于Gibbs抽样算法的三参数威布尔分布的Bayes 估计；乔世君等［7］讨论了基于Gibbs 抽样算法的定数截尾时威布尔分布的Bayes 估计；魏艳华［8-10］讨论了基于混合Gibbs 抽样算法的三参数威布尔分布，指数-威布尔分布和分组数据场合逆威布尔分布参数的Bayes 估计；熊常伟等[11]在熵损失函数下几何分布可靠度的先验分布分别为分布和幂分布时，给出了可靠度的EB 估计，并结合实际数据比较了两种先验分布下估计值的精度；龙兵[12]讨论了双边定时截尾下Pareto 分布的参数估计；刘荣玄等[13]讨论了三参数Pareto 分布在平方损失函数下的Bayes 估计和参数型经验Bayes 估计等；龙兵[14]讨论了双定数混合截尾下两参数Pareto 分布的统计分析；李凤等[15]基于逐步增加的Ⅱ型截尾样本,当Pareto 分布的尺度参数已知时，分别在LINEX损失和平方损失下讨论了其形状参数和可靠性指标的Bayes 估计；Pandey B N 等[16](2011)对形状参数已知的两参数威布尔分布的尺度参数做出了极大似然估计与Bayes 估计，并对Bayes 估计相对于极大似然估计的相对效率做了数值模拟；Saadati Nik A 等[17](2021)运用极大似然估计法、最小二乘法和贝叶斯方法（林德利近似法和马尔可夫链蒙特卡洛法）估计了一种新型Pareto 分布的未知参数；Shukla G 和Kumar V[18]（2018）研究了不同先验分布下Pareto 分布形状参数的Bayes 估计，同时还讨论了在Asymmetric Precautionary 损失函数与平方误差损失函数下形状参数的贝叶斯估计与极大似然估计等其它估计的比较。

本文基于Linex(Linear exponential)非对称损失函数，给出了两参数Pareto 分布的Bayes 估计，并且对Linex 损失函数下的Bayes 估计和极大似然估计的相对效率进行了模拟研究。

1 极大似然估计

Pareto 分布的概率密度函数表达式为

其中α是形状参数，θ为尺度参数。

设(x1,x2,…,xn)为来自总体的独立同分布样本，则似然方程为

对数似然方程为

先通过极大化似然函数得

2 两参数Pareto 分布的Bayes 估计

2.1 非正常先验下的后验分布

本文选取的先验分布为非正常先验分布：

则两参数的后验分布为:

其中x*=min{x1,…,xn}

2.2 基于Linex 损失函数的Bayes 估计

定义1Linex 损失函数最初是由Varian[19]提出的一种非对称损失函数，下面给出两参数的Linex 损失函数表达式：

定理1在Linex 损失函数(8)下，对于任一先验分布，参数α,θ的Bayes 估计分别为：

证明：设分别为α,θ的任一估计，在损失函数(8)下，对应的Bayes 风险函数为:

上式风险函数的左端E表示为关于样本x1,x2,…,xn的联合分布取期望，若欲求Bayes 解，则只需要极小化

接下来令

2.3 容许性

引理1[20]在给定的Bayes 决策问题中，假设对给定的先验分布π(θ)，θ的Bayes 估计δB(x)是唯一的，则它是容许的。

2.4 Gibbs 抽样

MCMC 中的Gibbs 抽样算法最初是由Geman 夫妇于1984 年提出的，并且Gibbs 抽样算法常适用于高维随机变量的模拟，本文将采用Gibbs抽样算法应用于Bayes 估计。

为了能够顺利的使用Gibbs 抽样算法从后验分布中进行抽样，首先需要得到两个满条件分布来作为转移概率。根据后验分布(7)，可计算出满条件分布：

从上面两个满条件分布可以看到，第一个满条件分布服从为伽马分布，进行抽样并不困难，而对于第二个满条件分布则利用以下逆变换方法进行采样。

逆变换：定义一个分布Mono(a,b)，其中a＞0,b＞0，拥有如下概率密度函数

并且对于0 ＜x＜b，分布函数为

在0 ＜x＜b上求分布函数F的逆：

因此，我们即可通过U～Uniform(0,1) 从Mono(a,b)中进行采样，令X=bU1/a（事实上，这是Pareto 分布的倒数，如果X～Pareto(α,θ)，那么，反之亦然。）

于是得到两个满条件分布分别服从：

3 模拟研究

在模拟研究中，首先通过R 软件中的actuar包生成了服从Pareto 分布的随机样本，并基于这些随机样本比较了极大似然估计与Bayes 估计的相对效率。样本容量分别为n=1 050 100。在比较形状参数α的相对效率时，α选取了1.5 至4，步长设置为0.25，θ=1；而在比较尺度参数θ的相对效率时，α=1.5，θ选取了1 至4，步长设置为0.2。对于Linex 非对称损失函数的尺度参数a，在模拟形状参数θ的相对效率时，选取了a=1,2,-1,-2 分别代表高估和低估的权重；在模拟尺度参数θ的相对效率时，选取了a=1,-1 分别代表高估和低估的权重。迭代次数M为1 000。

形状参数与尺度参数的风险分别为：

于是两参数Pareto 分布在Linex 损失下的Bayes 估计相对于极大似然估计的相对效率分别记为：

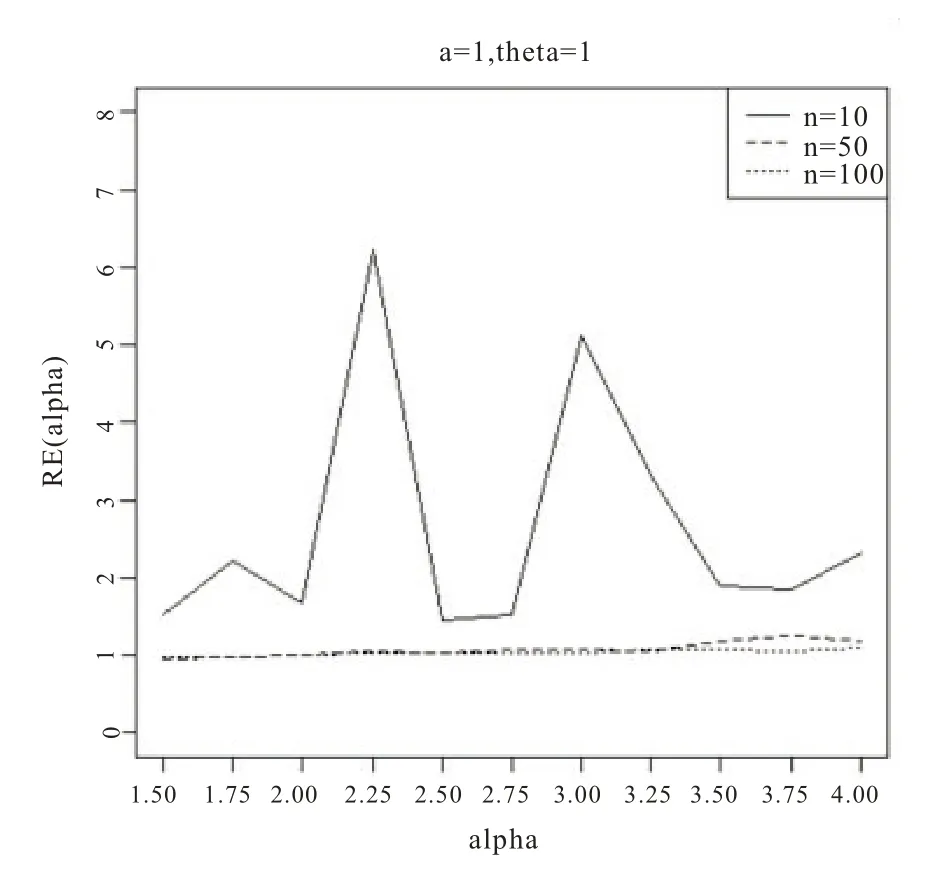
图1 基于a=1,θ=1

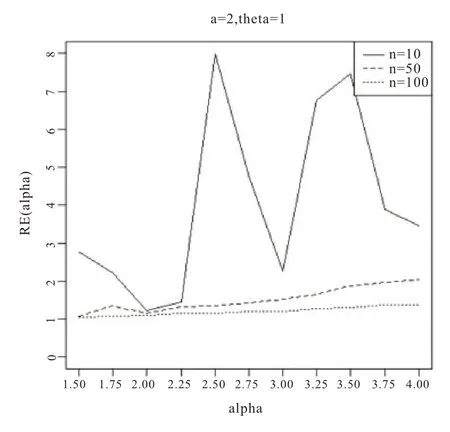
图3 基于a=2,θ=1

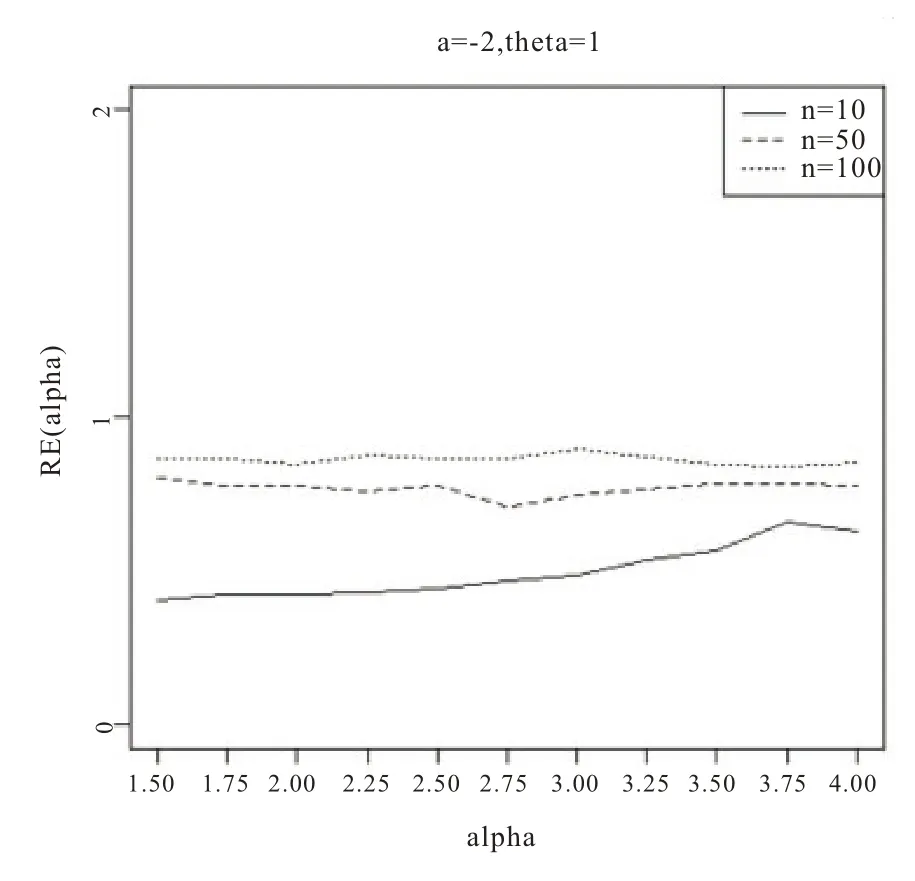
图4 基于a=-2,θ=1

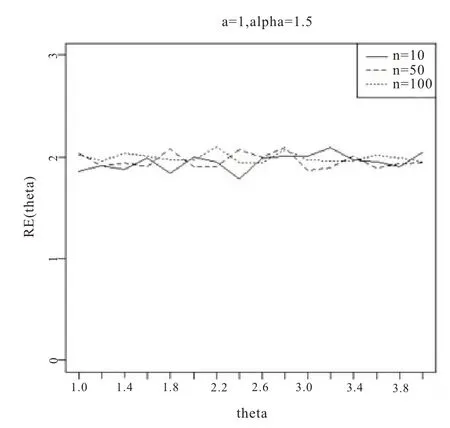
图5 基于a=1,θ=1.5

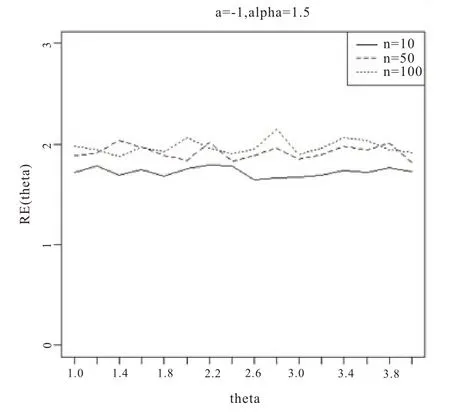
图6 基于a=-1,α=1.5

从图1-6 的结果表明，尺度参数θ的Bayes 估计效率要一致高于极大似然估计；而对于形状参数a：当a＞0 时，即高估的权重大于低估时，在小样本的情况下，Bayes 估计的效率要高于极大似然估计，而随着样本量的增加，两种估计方法的效率逐渐趋于相同；当a＜0 时，即低估的权重大于高估时，在小样本的情况下，极大似然估计的效率要高于Bayes 估计，而随着样本量的增加，两种估计方法的效率也趋于相同。

4 结论

本文首先给出了两参数Pareto 分布的极大似然估计，然后给出了基于Linex 损失函数下两参数Pareto 分布的Bayes 估计，并利用Gibbs 抽样算法进行了Bayes 估计实现，最后对两者估计的相对效率进行了数值模拟。结果表明尺度参数θ的Bayes 估计效率一致高于极大似然估计；在小样本情形下，当损失函数的尺度参数大于0 时，形状参数α的Bayes 估计的效率高于极大似然估计。所以在小样本情形下，对于形状参数与尺度参数的估计，Bayes 估计的效率是要明显优于极大似然估计的。事实上，在我们的现实生活当中，可能会经常出现一些高估比低估更关键的情形，并且高估应该被赋予更高的权重。例如，当分析一个地区的城市人口容量时，若大量的进行模拟研究，会给相关统计部门带来相当大的负担，因此在这些情形下，我们会尽可能的使用小样本。基于这些适用于小样本的情形，建议可在这些场景中使用Bayes 估计。