基于期望传播算法的多天线信号检测:架构、技术与挑战*

蒲旭敏,孙致南,宋米雪,陈前斌

(1.东南大学 移动通信国家重点实验室,南京 211189;2.西南交通大学 信息科学与技术学院,成都 611756;3.重庆邮电大学 通信与信息工程学院,重庆 400065;4.移动通信技术重庆市重点实验室,重庆 400065)

0 引 言

多输入多输出(Multiple-Input Multiple-Output,MIMO)技术是移动通信物理层关键技术。自第三代移动通信以来,MIMO因其诸多优点(如增加系统吞吐量,提升链路可靠性,提高频谱效率、能量效率等)而被广泛应用[1]。然而随着用户终端的增加以及通信业务的增加,性能提升存在瓶颈,天线规模亟需提升。如今大规模MIMO已是5G移动通信物理层关键技术[2],且超大规模MIMO技术已成为6G移动通信系统的关键潜在技术[3]。面向未来,天线维度必将得到进步一步扩大。虽然频谱效率、能量效率、空间分辨率等性能将得到进一步改善,但另一方面,能否提出低复杂度高可靠性的检测算法成为一个研究难题。

由于天线数量和用户数量的增加,传统检测算法面临挑战,如最大似然(Maximum Likelihood,ML)检测需要探测所有可能的符号矢量,这是一个NP难题,自然会在高维MIMO系统中面临瓶颈。传统线性检测算法如最小均方误差(Minimum Mean Square Error,MMSE)、迫零(Zero Forcing,ZF)算法等的优势在于实际系统中易于实现且在低维系统中复杂度可以接受,但在天线维度和调制阶数的进一步提升后,算法一方面仍面临矩阵求逆所带来的计算复杂度,另一方面性能也不够理想[4]。非线性检测算法,如球形译码(Sphere Decoding,SD)、树搜索(Tree Search,TS)等虽然表现出良好的性能,但其算法复杂度需随阵列维度的增加而迅速增加,以维持良好的性能。

近年来,基于消息传递(Message Passing,MP)的信号检测器得到了广泛研究。MP是一种优良的方法,它能够将高维问题低维化。精确的消息传递算法如置信传播(Belief Propagation,BP)已得到了一定的研究[5],它通过迭代更新传输符号的后验分布,获得了良好的性能,但计算复杂度仍然很高,且在高维MIMO系统中由于因子图“环路”的存在而显现出严重的性能损失。本文讨论的期望传播(Expectation Propagation,EP)[6]是BP的广义化,与BP相比它不用传递整个分布的样值,而只需要通过矩匹配来传播矩信息,因此EP与BP相比拥有更低的复杂度,被大量运用在贝叶斯推断中。高斯树近似(Gaussian Tree Approximation,GTA)[7]克服了高斯树近似中的环路效应,构造了后验分布的高斯树近似,并且依赖于BP来传输符号的近似后验分布。通过连续干扰消除(Successive Interference Cancellation,SIC)结合的GTA-SIC算法改进了GTA算法,曾被认为是在较大型MIMO系统中有效检测的优良方案,但将EP用于MIMO检测的工作中,已实际证明EP具有比GTA更优越的性能[8]。

原始EP的算法复杂度为O(LK3),K为发射天线数,L为算法迭代次数。根据实际仿真,一般算法迭代5次左右已可得到收敛,即算法不会因过量的迭代次数而带来额外的计算复杂度。且EP附加的为每个接收符号提供后验估计以作为一种软输出,该估计可以自然地馈送到信道解码器,而前述方法不能提供这样的估计,或者估计不准确。故面对未来超高维MIMO系统,使用EP算法进行“更快、更强”的低复杂度信号检测似乎是一种先进的方案之一。

最近EP已被运用到一些MIMO检测工作中,但目前缺少对EP算法进行多天线信号检测的综述性分析,相关研究人员缺少直观的学习参考。考虑到EP算法在6G诸多关键场景及关键领域进行信号检测的出色潜力,本文对EP多天线信号检测进行综述,并指出可行的未来研究方向,旨在为相关研究人员提供参考,推动6G超高可靠通信的达成。

1 基于EP的MIMO信号检测架构

1.1 典型系统模型

考虑一个典型上行MIMO系统,发射端有K个单天线用户,接收端BS配置N个接收天线,如图1所示。

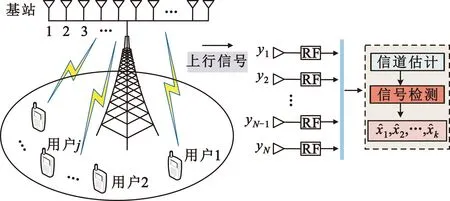
图1 典型MIMO信号检测系统模型Fig.1 Typical MIMO signal detection system model

将K个用户的发送符号定义为一个K维向量组x=[x1,x2,…,xK]∈Θ,Θ表示符号星座集,系统输入输出模型如下:

y=Hx+n

(1)

式中:y∈N表示接收端向量;H∈N×K是信道矩阵;n∈N是N维加性高斯白噪声,它服从分布CN(0,σ2IN)。信号检测即在已知接收信号y和信道矩阵H后通过硬判决或软判决得到对x的估计。该模型为一般化上行MIMO信号检测模型,是后续所述多种EP检测方案的基础模型,具有一般意义。

给定上述模型的情况下,所发送的符号向量x的后验概率具有以下表达式:

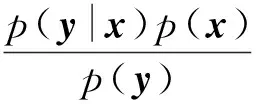
(2)

式中:p(x)代表x的先验分布;p(y|x)代表似然函数;p(xk)和fn(yn|x)分别代表一个边缘先验分布和一个边缘似然函数。这是经典的贝叶斯后验分布模型。若对输出做软判决,即计算对数似然比(Log-Likelihood Ratio,LLR),必然需要计算后验分布;若对输出做硬判决,则需要计算后验分布的均值,故对后验分布的推断十分重要,EP即是一种用于贝叶斯推断的有效方案。

1.2 算法原理

基于给出的模型,本小节讨论EP基本算法原理。原始EP的基本原理是通过一个易处理的分布q(x)近似一个难处理的分布p(x),以此使得p(x)与q(x)的Kullback-Leibler(KL)散度最小化。这等效于对p(x)和q(x)做矩匹配[6],使得p(x)与q(x)的一阶矩和二阶矩即期望和方差相等匹配。式(2)可以改写为

(3)

式中:Ⅱxi表示符号xi的先验概率。EP考虑使用一个指数族分布q(x)以近似p(x|y),其形式为

(4)

式中:γi和Λi是代指某个维度下高斯特性的参数。根据这两个参数所构成的向量γ和Λ得到q(x)的方差和均值形式如下[8]:

(5)

(6)

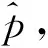
(7)

式中:q(xi)代表的第i个边缘分布,并定义 “空腔函数”为

(8)

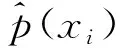
(9)

(10)

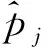
(11)

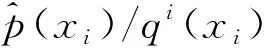
(12)

由此更新完所有的γi与Λi后即完成了一次算法迭代。最终算法迭代截止时,取当前的后验均值μ为符号向量估计值。更加形象的EP检测架构如图2所示。

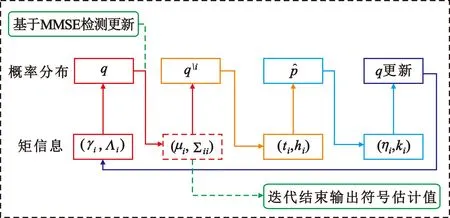
图2 基于EP的多天线信号检测架构Fig.2 Multi-antenna signal detection architecture based on EP

期望传播算法信号检测流程如下:

输入:y,H,σ2,迭代次数L;

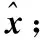
2 forl=1:Ldo

5 ∑(l)=(σ-2HHH+Λ(l))-1

6μ(l)=∑(l)(σ-2HHy+γ(l))

7 fori=1:Kdo

15 end for

16 end for

考虑一个MIMO上行传输系统,基站端配备N=32根天线,在同一时频资源下服务K=8个单天线用户,采用BPSK调制,不考虑编码,信道采用瑞利信道,得到不同信噪比(Signal-to-Noise Ratio,SNR)下的误码率(Bit Error Rate,BER)曲线,如图3 所示。可以发现,EP检测器在仅迭代4次时已具有显著的性能优势,逼近最优检测算法ML。

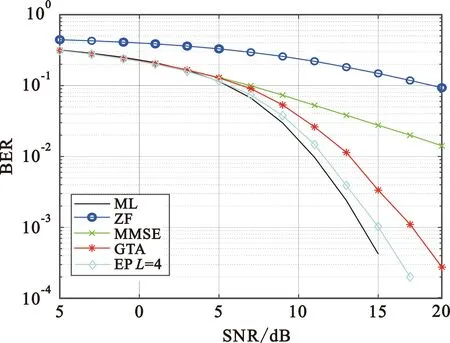
图3 信号检测算法性能对比Fig.3 Performance comparison among signal detection algorithms

同时测试不同迭代次数下EP算法的性能表现,结果如图4所示。可以发现,随着迭代次数的提升,EP检测算法逐渐趋于收敛,且迭代50次与迭代4次时的误码率性能几乎一致,这证明EP算法的收敛速度较快,在少量的迭代次数下即可逼近最优检测算法ML的性能表现。同时也说明EP检测算法并不需高额的迭代次数,计算开销有限,是一个可用作低复杂度高性能信号检测工作的有效方案。

2 基于EP的MIMO信号检测技术

2.1 算法低复杂度设计

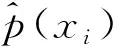
文献[13]提出了一种逐次更新的EP(Successive Updating EP,EP-SU),以此来避免每次迭代中的求逆,同时加快收敛速度。简单来说,原始EP得到更新的矩信息需获得所有的(γi,Λi),而EP-SU获得某边缘矩信息(γi,Λi)后即立刻更新矩信息矩阵。最终得出EP-SU相比于原始算法复杂度更低,这种优势随着天线规模的提升而提升,故而十分适合大规模MIMO,且这种算法比原始算法收敛速度更快,但该方案第一次初始化时求逆复杂度仍为O(K3)量级。

实际上现有部分EP检测方案(如文献[25])在矩信息更新部分未使用MMSE闭式解,而采用概率统计原理进行数值积分求解期望与方差,故而不存在求逆步骤。但这种方式需要基于符号软信息事先计算先验分布,并需要在星座空间大小内进行积分,实际还称不上低复杂度方案。

为更加直观地给相关研究者提供参考,表1中列出了ML、MMSE、ZF、BP检测算法与几个典型EP检测算法的计算复杂度,其中以数值乘法运算量作为复杂度衡量指标,L,LEPA,LEP-NSA分别表示三种EP方案的迭代次数,J代表级数展开的最大截断项。可以发现,原始EP算法基本与MMSE、ZF等基于求逆的线性检测方案复杂度量级相当,复杂度量级均为O(K3)。

表1 算法复杂度对比Tab.1 Comparison of algorithm complexity

2.2 基于概率图模型的EP检测算法

Minka[14]最早提出了期望传播在消息传递上的应用,并给出了因子图下EP消息更新规则。它与上一小节提到的原始算法在本质上没有区别,只是将因子图与和积算法[15]运用到了EP算法迭代过程。因子图是一种概率图模型,MIMO信号检测后验模型可以用概率图模型来概括,所以使用消息传递与因子图来完成信号检测是很自然的。

因子图的模型本质是将高维问题低维化,则对于需处理的高维联合概率问题很容易想到是否能将其因子化处理[25-27]。以文献[26]为例,它将消息传递的和积算法与EP原理相结合生成了所提出的模型。其原理是将所需要传递的后验概率变成因子的乘积形式,即将公式(13)转换为公式(14):

p(x|y)∝p(y|x)p(x)

(13)

(14)

式中:f0表示先验分布;用fc代表一个边缘似然函数;C为总的边缘似然数目。先验概率由f0(x)给出,其他因子节点(Factor Node,FN)(f1,f2,…,fC)代指各边缘似然函数,对应的因子图模型见图5。

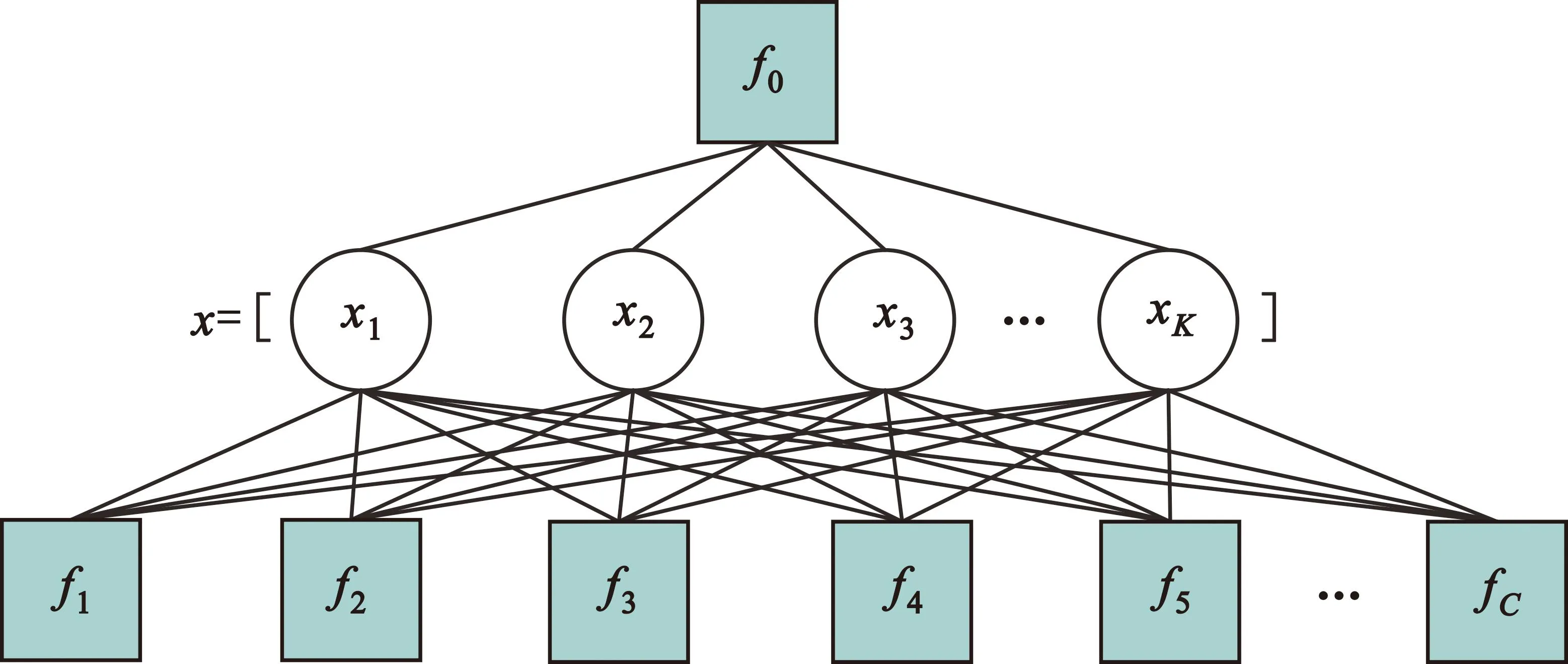
图5 因子图模型Fig.5 Factor graph model

图5中,方形代表因子节点,圆形代表变量节点(Variable Node,VN),消息传递则表示FN和VN之间的信息迭代过程。基于文献[14]给出的消息传递规则,它们之间的约束关系由和积算法表示为

(15)

(16)

式中:mxj→fc代表由VN到FN传递的信息,mfc→xj则代表由 FN到VN传递的信息。

由和积算法的原理知,发送符号xj的边缘后验分布为

(17)

结合式(15)则有

p(xj|y)=mxj→fc(xj)mfc→xj(xj)

(18)

该边缘分布亦被称为置信度,EP算法的核心思想是用一个易处理的置信度来近似真实的边缘后验分布。假设符号xj的近似置信度为b(xj),其属于指数族分布F(一般取高斯分布),它实际相当于上一节提出的指数族分布q(xj),由下式给出:

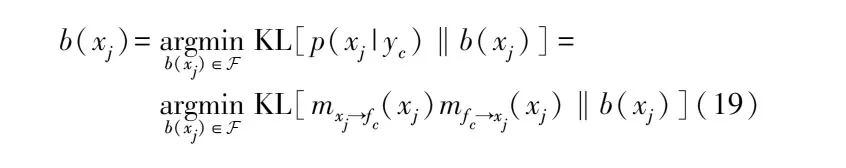
(19)

式中:KL[·‖·]代表KL散度运算,它用来衡量两种概率分布之间的差异程度。然而通过数值计算并得到KL散度的最优化参数涉及高维积分,显然复杂度较高。两个概率分布的KL散度最小化等价于矩匹配,矩匹配的含义为两个概率分布的矩信息相等,例如对于一个高斯分布而言,若一阶矩信息即期望和二阶矩信息即方差相等,则两个分布相等。对于需处理的两个分布,若能通过某种方法使得近似分布的期望和方差逼近真实分布的对应矩信息则认为完成了矩匹配,即完成了KL散度最小化,EP则正是依据矩信息完成算法迭代更新。

基于因子图的EP算法实质是依据mxj→fc与mfc→xj两种信息的矩信息进行EP算法更新,其底层逻辑与上一小节提到的原始算法在本质上没有区别,但适合更直观地适配到一些具体场景,例如分布式阵列架构,后文将进一步说明。

研究人员已经提出了因子图EP算法的一般形式[16],并且在这一基础上又对基于因子图的EP算法做了进一步改善[17]。文献[17]提出了一种近似最优的基于稀疏码多址(Sparse Code Multiple Access,SCMA)的低复杂度EP算法,称为稀疏信道EP算法(Sparse Channel Expectation Propagation,SC-EPA)。因为EP算法的复杂度很大程度上取决于需要传递消息的数目,故而SC-EPA相比于传统EP做了三点改进:第一,考虑了信道的稀疏性,当信道矩阵的某些列趋向0时,因子图中对应的两个点之间没有消息传递,故消息传递数量将大大减少;第二,改变了VN和FN之间消息传递的更新方法,降低从VN到FN消息传递的倒数计算次数;第三,去中心化处理FN,将FN分配为多个子簇,并成功证明可以在微小性能损失下降低复杂度。

文献[18]在接收端考虑低精度数模转换器(Analog to Digital Converter,ADC),且将MIMO信号检测问题建模为广义线性逆问题,得到了一种基于EP原理的改进型检测算法,称为广义期望一致(Generalized Expectation Consistent,GEC)算法。该算法实际是基于EP算法在因子图上增加线性空间节点,即将信道矩阵对信号的投影作为一种变量节点参与到消息传递的运算过程中,以改善检测性能。

文献[19]与[20]深入研究了概率图模型的变体,并将EP算法作为其核心组成部分。文献[19]将BP与平均场(Mean Field,MF)结合提出了一种低复杂度变体,并将离散BP和高斯BP(等同于EP)因子图连接在一起,提出了用于信号检测的组合BP-MF-EP消息传递算法,且结果证明性能几乎与精确BP-MF框架相同。文献[20]同样提出了用于MIMO-OFDM系统的消息传递接收机,通过引入辅助变量,进一步将每个观测因子分解为若干子节点,混合使用MF、BP和EP处理观测因子,最后根据数值分析发现所提出的接收机要明显优于现有接收机。

2.3 深度学习赋能的EP检测算法

EP作为一种迭代更新算法,可以考虑增添阻尼因子以牺牲部分收敛速度为前提而得到更精确的解。具体来说,添加取值范围在[0,1]区间的阻尼因子β,使得矩信息的更新值变为

Λ(l+1)=(1-β)Λ(l)+βΛ(l-1)

(20)

γ(l+1)=(1-β)γ(l)+βγ(l-1)

(21)

然而阻尼因子的选取往往来源于经验值,一个最为精确的阻尼因子并无法通过显示解得到。这使得研究人员意识到可以将深度学习与EP算法相结合,得到模型驱动的检测算法。这提供了6G深度学习赋能通信场景中,EP检测算法的应用前景。

基于EP算法的模型驱动信号检测方案,通过将EP算法展开为可学习的多层网络,动态调整算法参数。具体而言,EP算法的每次迭代过程被定为网络的一层,每次算法迭代更新的矩信息定义为该层网络的输出,上一次更新的矩信息被定义为输入,一共L次算法迭代则对应L层网络。神经网络负责提供每层网络需要的可学习参数,例如阻尼因子,其一般化架构可参见图6。

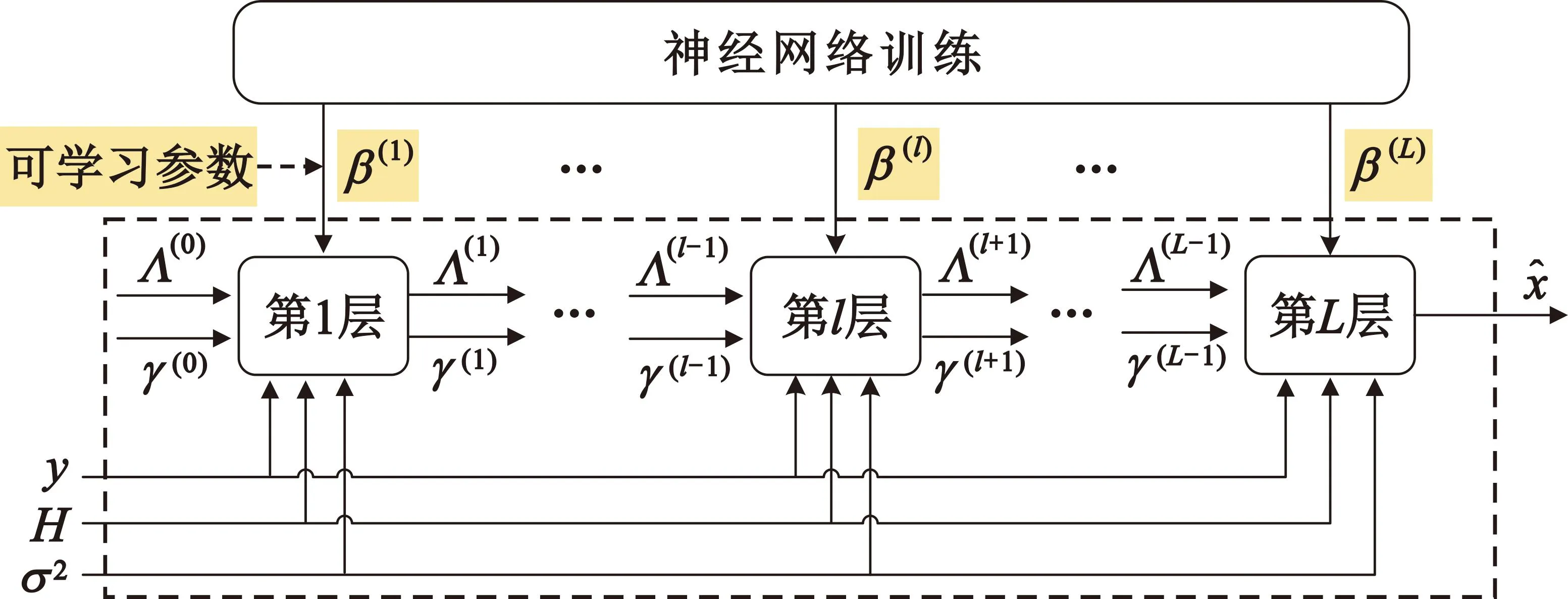
图6 基于深度学习的EP算法展开结构Fig.6 Unfolding structure of EP algorithm based on deep learning

文献[21]通过将EP算法与深度学习方案相结合,将算法的阻尼因子与初始方差作为每层网络的输出,以构成模型驱动的深度学习EP检测算法,性能显著优于元素EP检测器,且具有鲁棒性。文献[22]采用了类似的方式,且通过增加阻尼因子以改善不同信道相关度下的信号检测性能。

文献[23]基于EP算法使用一种Hypernetwork网络完成不同信道条件和噪声条件下的信号检测框架,该框架可以自动确定基于EP展开的MIMO检测器的内部参数,以适应变化的条件。该方案进行了现实原型机的仿真实现,这是第一个实际实现深度学习与EP算法相结合的信号检测工作。

文献[24]提出了模型驱动的Turbo-MIMO接收机,使用短导频序列通过线性最小均方误差算法来生成信道矩阵的初步估计,将EP算法表示为多层深度前馈网络来优化接收器的阻尼系数,从而在接收机中实现信号检测,可以有效补偿信道估计误差。这种思想的提出源于研究人员注意到以往的研究主要是基于完美信道状态信息,而对于快衰落信道这不是一个理想假设。信号检测器通过将EP表示为多层深前馈网络,称为EPNet,以优化阻尼因子从而实现信号检测。EPNet的功能是平衡信道估计器和信道解码器之间的估计误差。数值结果表明,所提出的模型驱动的Turbo-MIMO接收机明显优于现有算法,并且对于导频序列不足的信道估计是有效的。

2.4 面向6G新型阵列架构的EP检测算法

EP算法涉及的边缘矩信息更新可与实际场景下的分布式阵列架构良好结合,尤其是在诸多面向6G的新型阵列架构下具有显著应用前景。文献[25]考虑大规模MIMO场景下的分布式阵列设计,将EP算法很好地与分布式阵列结构相适配。文献[26]和[27]考虑超大规模MIMO场景下的空间非平稳特性,设计子阵化MIMO检测架构,通过矢量化因子图很好地将EP算法与阵列结构相结合,每个子阵处理本地信息并将信息汇总于中央处理单元进行合并处理,中央处理单元反馈信息个每个子阵作为下一次迭代的先验信息。图7 直观地对子阵化检测架构进行了描述,基站端N根天线被分成C个不相交的子阵列处理单元(Subarray Processing Unit,SPU),每个子阵列中的天线数为Nc。

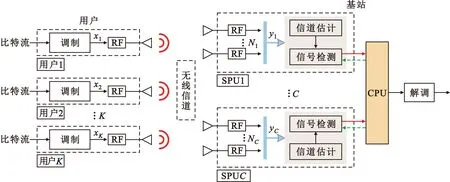
图7 子阵化超大规模MIMO信号检测架构Fig.7 Subarray extra-large scale MIMO signal detection architecture

每个子阵的信息将汇总到中央处理单元(Central Processing Unit,CPU)进行合并处理。每个子阵列都配有独立的信号处理单元,第c个子阵列的等效基带接收信号模型为

yc=Hcx+nc

(22)

式中:yc表示第c个天线子阵列接收到的符号向量;Hc∈Nc×K表示该子阵下的信道矩阵;nc是第c个天线子阵列中的加性高斯白噪声。基于该模型,符号后验推断问题可以建模为

(23)

同样该模型可被转换为因子形式:

(24)

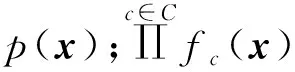
第c个子阵列中第j个用户符号xj的实际后验概率表示为

(25)

结合前述消息传递原理,等效得到

p(xj|yc)∝mxj→fc(xj)mfc→xj(xj)

(26)

定义置信度bfc(xj),其属于指数族分布F,用其表示第c个子阵列中检测符号的近似后验分布,则依然可依据消息传递规则对矩信息进行更新。在图5所示模型中,由于所有变量节点与因子节点全连接,将因子节点统一设置为一个矢量变量节点x,则此时第c个子阵的矢量置信度为bfc(x)。bfc(x)作为近似后验分布,其均值和方差由同样由MMSE估计生成。基于该思想,子阵化架构下每个子阵实际构成了一个因子节点,而节点信息的更新则实际对应各子阵与中央处理单元间的信息交换,这使得算法完美适配实际阵列结构。

文献[26]与[27]均采用了上述超大规模子阵化阵列架构进行EP检测算法设计。文献[26]侧重对子阵化EP算法的理论分析与推导,包括算法收敛性不动点分析等。文献[27]侧重于子阵化超大规模MIMO系统中低复杂度EP检测算法的设计和分析讨论。文献[27]包括了本文作者的研究工作,现对基本的仿真结果进行说明。

以误码率作为信号检测性能指标,采用16QAM调制方式,所有信号均叠加加性高斯白噪声(Additive White Gaussian Noise,AWGN)。不考虑编码和解码方案,且由于主要工作为信号检测,均假设信道完美已知。EP算法迭代次数均为L=5。整个阵列被分为4个子阵,每个子阵内天线数平均分配,即N=C×Nc(C=4),基站端总天线数N=1 152,总单天线用户数为K=128。如图8所示,可以发现集中式EP算法性能显著优于传统检测算法MMSE,且子阵化EP检测器性能接近集中式EP检测器,这证明子阵化信号检测架构是有效的。

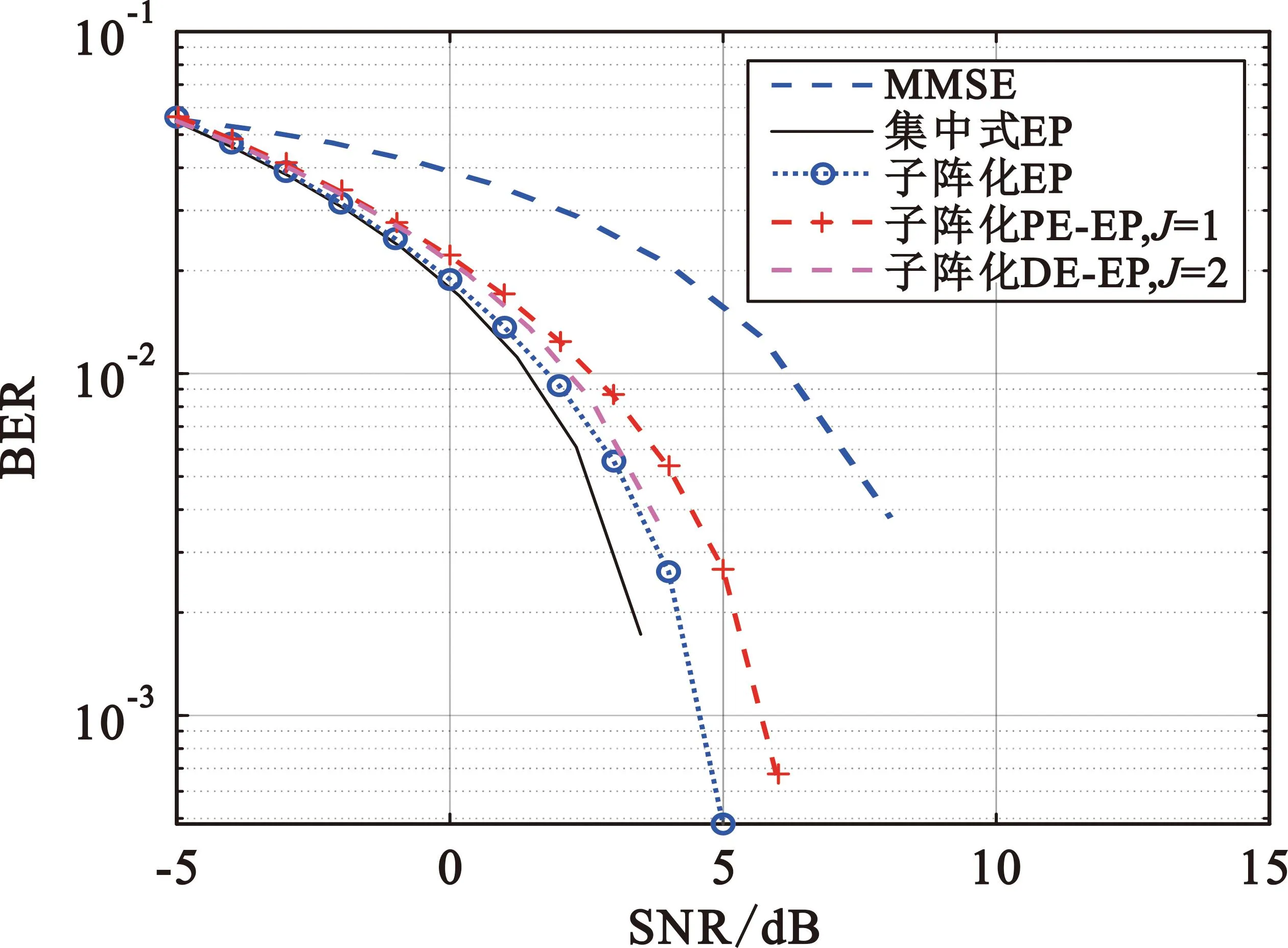
图8 子阵化超大规模MIMO信号检测性能分析Fig.8 Performance analysis of subarray extra-large scale MIMO signal detection

文献[28]将EP算法用于无蜂窝(Cell-Free,CF)大规模MIMO场景的信号检测工作,提出了用于无蜂窝大规模MIMO的分布式EP检测器,将每个接入点(Access Point,AP)作为一个因子节点,并与中央处理单元进行信息交换。文献[29]采用了同样的思想,并在计算后验信息时结合导频污染的影响,得到了增强型EP检测器。在无蜂窝场景中的应用,其本质仍是利用了EP算法与分布式处理架构的良好适配性。

2.5 检测性能分析与改进

检测性能的研究对EP算法的理论发展极为重要,尤其是为未来6G多种场景下EP检测算法的使用具有指导意义。EP已被证明在满足大系统条件下可以达到贝叶斯最优性能[30]。同样在文献[31]中,EP算法的收敛性也通过状态演化方程得到了严格证明,然而状态演化分析需要在大系统条件下使用统计特性得到,即发送天线和接收天线数目都趋于无穷(K→∞,N→∞)。

然而,大系统条件(K/N=α

2.6 技术扩展与结合

研究人员还将多种技术与EP相结合来进一步提升EP的应用能力,例如格基规约、收敛感知、编码技术等。

文献[33]将格基规约(Lattice Reduction,LR)技术与EP相结合,提出了一种格基规约辅助的EP检测算法(Lattice Reduction Aided Expectation Propagation,LRA-EP)。它采用LR技术中的(Lenstra-Lenstra-Lovasz,LLL)算法对原线性模型中的信道矩阵做处理,使得处理后的信道矩阵趋于正交,EP算法用于近似新构造的后验检测量。提出的LRA-EP算法比传统MMSE算法和原始EP算法都要优越,同误码率下所需要的信噪比条件最低。

文献[34]提出了一种基于收敛感知的EP检测器,主要思想是减少不必要的迭代过程,基于用户终止、天线终止和码本缩减,可以在性能略有损失的情况下减少迭代计算次数,降低计算成本,并具有性能增益。

文献[35]将EP应用于LDPC编码的MIMO系统中,希望获得可进一步用于符号检测或软解码的软判决信息。EP作为一种良好的的近似推理技术,可以构造对给定概率分布的近似,大大简化了软比特信息的边缘概率计算。在现有的软输出MIMO检测方法中,由于EP能够准确估计每个编码比特的后验概率,因此在与LDPC编码系统相结合时能够提供优异的性能,与其他文献中类似的低复杂度LDPC-MIMO译码方法相比,性能得到了显著的提高。

3 研究挑战

通过以上综述可知,基于EP算法的多天线信号检测研究已经取得一定成果。EP作为一种优秀的贝叶斯推断算法,是目前最先进的检测算法之一,有望在6G实际场景中得到推广。目前的研究工作聚焦于EP复杂度与性能的改善,同时通过与多种技术、场景相结合得到更优的信号检测器设计,如表2所示。

表2 基于EP的多天线信号检测方案总结Tab.2 Summarization of multi-antenna signal detection schemes based on EP

但是,现有的基于EP检测的各种研究仍然具有局限性与不足,未来需从以下方面进行研究:

第一,非理想信道条件的检测算法设计。由以上归纳发现,现有方案大多基于已知理想信道状态信息或者基于瑞利衰落而进行,但实际情况下无线信道状态信息往往并不完美且不拘泥于瑞利信道假设,它受到多种实际情况的影响且与信道估计误差息息相关。因此,如何设计EP算法使之在未知完美信道的情况下得到理想的信号检测性能是一个待研究的方向,这包括设计兼顾非完美信道的检测算法以及完全未知信道的盲信号检测算法设计等。

第二,面向6G超大规模MIMO场景的检测算法设计。EP在超大规模MIMO场景下具有显著的“适配性”优势,但仍需继续进一步匹配信道特性:一方面EP是一种基于MMSE的迭代更新算法,超大阵列下显著的信道正交性将为算法带来性能增益;另一方面超大规模MIMO的分布式结构将能够很好地适配EP可能的分布式结构,特别是基于矢量因子图的EP检测过程。但针对超大规模MIMO显著的信道特性还有诸多研究点值得探究,例如球面波前下的低复杂度信号检测问题;信号在角度域不再具有稀疏性,如何设计得到低复杂度的EP信号检测算法等。结合超大规模MIMO显著的信道特性,EP算法还需要做诸多变体以适应信道特性,这值得未来进一步研究。

第三,面向6G分布式场景的检测算法设计。面向6G的诸多分布式处理场景,研究如何将期望传播算法分布到多个计算节点上,以实现高效的分布式信号检测,降低计算复杂度,并减少通信开销是有意义的研究方向。上文所述无蜂窝MIMO场景是一个良好的应用示例,除此之外6G海量机器通信也为这一应用提供了可能,即EP信号检测在物联网场景也具有极高应用潜能。

第四,深度学习与EP的进一步融合。本文已阐述了部分基于EP的模型驱动信号检测方案,但现有研究主要将可学习参数聚焦于阻尼因子上,对检测性能的提升有限。可针对EP进行深入的性能理论分析,提取影响EP检测性能的关键参数,包括迭代初值、噪声方差等,得到更多样化的可学习因子以进一步提升算法性能。此外,考虑如何将深度学习模型与期望传播算法结合,以在实时通信系统中实现低延迟和高效的计算也对深度学习驱动的EP检测算法具有重要意义。

第五,自适应EP信号检测算法。现有方案缺乏自适应EP检测技术研究。具体而言,自适应EP算法的核心目标是根据实时的信道条件、系统参数和环境特性来动态地调整其内部参数和迭代策略,以最大程度地提高检测性能、适应性和鲁棒性。例如,在信道条件差的情况下,可以选择更保守的参数设置以确保可靠性,而在良好的信道条件下可以采用更激进的设置以提高性能。此外,算法可以动态调整迭代的次数或停止条件,以在不同信道条件下达到最佳性能。在高信噪比下,可以减少迭代以降低计算开销,而在低信噪比下可以增加迭代以提高检测性能。

第六,低精度量化EP信号检测算法。由于降低硬件成本与系统功耗的迫切需求,低精度模数转换器(Analog-to-Digital Converter,ADC)在超大规模MIMO以及毫米波等系统中的应用被进一步挖掘。考虑到硬件限制,研究如何在有限精度计算环境下有效实施EP检测算法,以减少计算复杂度和能耗具有现实意义。了解有限精度计算可能引入的误差如何传播并影响概率推断,同时研究如何设计算法,以最小化这些误差的影响。

第七,原型平台测试与搭建。目前针对EP的诸多检测算法均停留于理论分析,缺少原型平台硬件测试。实际系统中的应用和性能验证是研究中至关重要的一步,它涉及将期望传播算法投入实际大规模/超大规模MIMO通信系统并进行全面评估的可能,这对EP检测算法用于6G实际通信场景至关重要。

4 结束语

本文对基于EP算法进行多天线信号检测的基本架构、现有技术、方案进行综述,分别从算法低复杂度化、基于概率图模型的EP检测算法、深度学习赋能的EP检测算法、面向6G新型阵列架构的EP检测算法、算法检测性能分析与改进与算法技术扩展与结合6个方面展开讨论,为相关人员提供基本研究路线,以对EP多天线信号检测算法产生直观认识。同时对未来研究进行展望,指出了7个未来工作可聚焦的具体领域,为相关人员进一步研究提供可行参考,以使得EP检测算法可实际服务于未来6G通信场景,解决实际需求。