基于DDPG的综合化航电系统多分区任务分配优化方法*

赵长啸,李道俊,汪鹏辉,田 毅

(1.中国民航大学 安全科学与工程学院,天津 300300;2.民航航空器适航审定技术重点实验室,天津 300300)

0 引 言

随着信息技术、高性能计算技术和航空电子技术的发展,综合模块化航空电子(Integrated Modular Avionics,IMA)系统已经成为当前民用航空领域的主流架构。相较于传统的分立式、联合式航电系统,IMA系统将多个独立的子系统综合起来,具备多个应用同时共享系统内软硬件资源的能力[1],在提高资源利用率、增强系统灵活性和适应性等方面具有很多优势[2]。航电系统作为飞机的“大脑”与“神经中枢”,其任务的执行不仅有较高的资源保证需求,对实时性也有严苛的要求,对于超出规定时限的任务,即使完成也会被判定任务失败,并直接影响飞机的飞行安全。因此,有效、合理的分区任务分配方法成为保证航电系统任务有效执行的基础,该问题也受到了学者和航电系统研发单位的重视。

航电系统任务调度问题主要涉及任务分配、任务优先级分配、可调度性分析[3]等问题,其中首先需要解决的是在满足可调度性[4]前提下,如何在多个分区内进行任务分配。文献[5]通过模拟退火算法解决实时系统的任务分配问题,文献[6]通过基于模拟退火的改进Q学习算法来对软件和硬件资源进行重构配置,重新分配任务方案。文献[7]将基于遗传算法的多目标优化方法应用于实时任务的调度问题。文献[8]在确保任务模块间执行顺序的前提下,采用分支定界的启发式算法,保证任务的实时调度。文献[9]提出一种基于序贯博弈多智能体强化学习的IMA系统重构方法,根据应用软件优先级确定博弈顺序,模拟应用软件重新分配过程,优化任务分配策略。随着计算技术的发展,以深度学习和强化学习为代表的人工智能技术主要运用于对数据的分析处理,深度强化学习结合了深度学习较强的感知能力和强化学习优秀的决策能力,已经成功应用在自动驾驶、资源分配、机器控制和优化调度等领域中,为复杂系统的决策问题提供了新的思路。航电系统任务在多分区内的分配优化,属于决策制定的优化问题。基于此,本文选择深度强化学习的算法作为优化问题的求解方法。

综合模块化航空电子系统相较于传统航电系统在配置灵活性、综合性以及硬件集成度方面均有改进,为了充分利用系统软硬件资源,提高系统性能,本文提出一种基于深度确定性策略梯度(Deep Deterministic Policy Gradient,DDPG)的任务调度优化算法,对任务集合在不同分区之间的分配调度进行优化。

1 系统模型

IMA系统是高度集成、资源共享的开放式平台[10],通过分区技术进行航电功能的驻留,一个处理节点可以包含多个分区。本节对航电系统分区及任务模型进行建模。

1.1 综合化航电系统模型

IMA系统通常采用分布式的处理框架[11],系统内含有多个通过AFDX网络相连接的嵌入式处理节点,每个处理节点内可设置多个分区,每个分区内可分配一个或多个预先定义的实时任务,如图1所示。

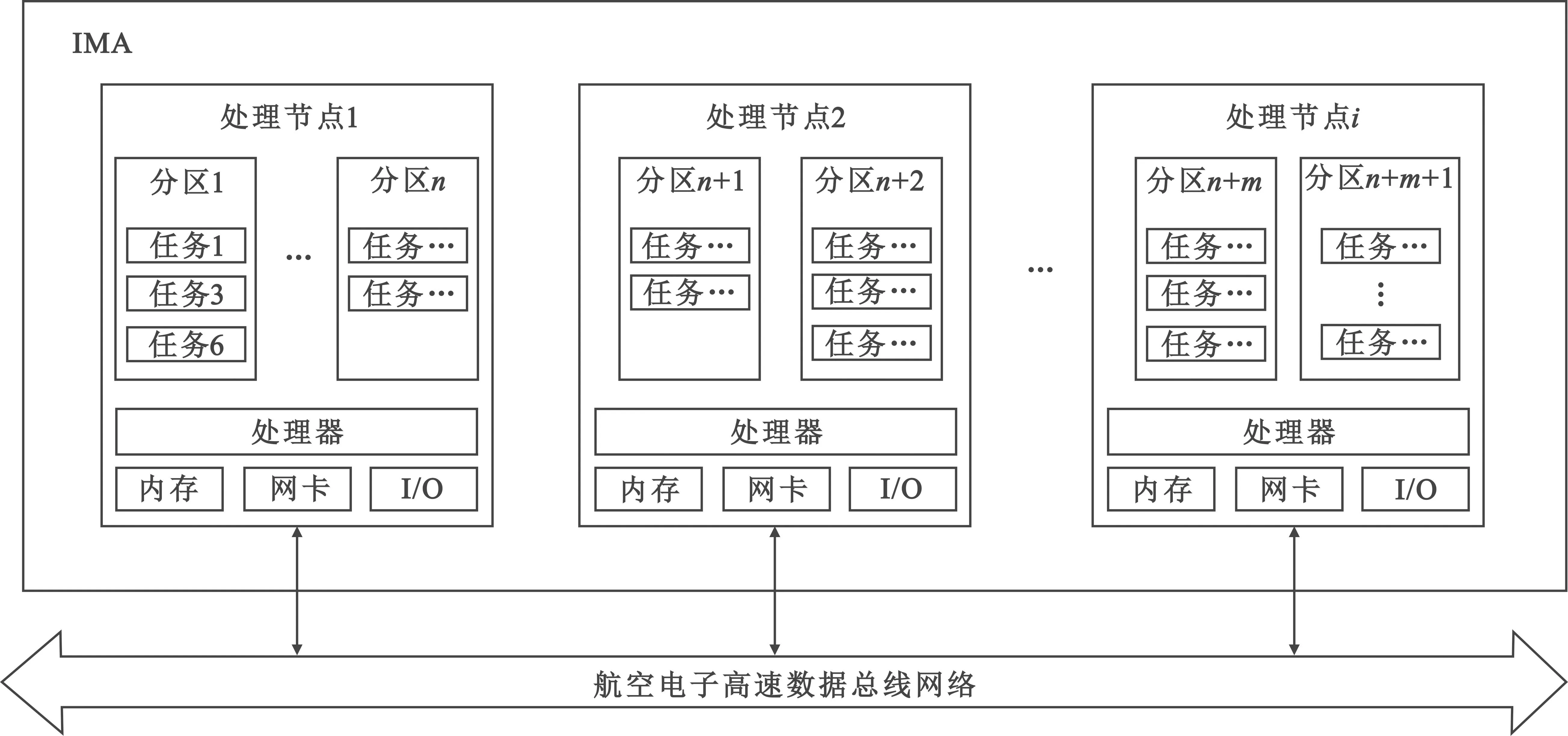
图1 IMA系统框架Fig.1 IMA system framework

1.2 处理节点集

IMA系统内包含一组同构的处理节点,处理节点通过端系统连入AFDX网络,并可以通过多级交换机实现信息的交换。

处理节点集可以表示为

N={Ni|1≤i≤nN}

(1)

式中:nN表示系统内处理节点的个数。每个处理节点都有内存、执行时间和带宽等资源上限,令M表示各处理节点的内存资源上限,T表示各处理节点的处理能力,B表示各处理节点的带宽。综上,处理节点可表述为一个三元数组Ni(Mi,Ti,Bi)。

1.3 分区集

在ARINC 653标准中,分区的定义指的是对航空电子功能按照某种策略进行分组,对运行在核心模块上的多个应用程序按功能可划分为多个分区。分区内的所有任务共享分区所占有的系统资源,操作系统对分区所占用的处理时间、内存和其他资源拥有控制权,从而使得处理节点中各分区相互独立。分区集可以表示为

P={Pi|1≤i≤nP}

(2)

式中:nP表示系统内所有处理节点内分区个数之和。每个分区有以下属性:所属的处理节点序号C;内存资源占用系数αM,表示所占用的处理节点内存资源比率;处理资源占用系数αT,表示所占用的处理节点处理能力比率。

1.4 任务集

航电系统通过在系统平台驻留应用实现系统功能,不同的航电系统通过任务进行具体功能的实现。一个航电功能内的按顺序执行的所有任务称为一个任务集,任务可以按照一定的策略在多个分区内进行执行,以满足任务资源需求与实时性需求。

任务集表示为

G={Gi|1≤i≤nG}

(3)

式中:nG表示系统内应用程序的个数,即任务集的个数。每个任务集由以下属性组成:任务集负载GL,任务集内所有任务负载之和;任务集所需内存资源GM,任务集内所有任务所需内存资源之和;任务集所在的分区序号GC;任务集在分区内的优先级GP。

综上,任务集可以表述为一个四元数组Gi,Gi中包含的任务记为{τi,1,τi,2,…,τi,n},任务τi,j可以描述为一个三元数组τi,j=(GLi,j,GMi,j,GDi,j),GLi,j表示任务τi,j的负载,GMi,j表示任务τi,j所需内存资源,GDi,j表示任务τi,j的截止时间。

同一个任务集内的任务可以不限定在同一个分区内执行,可以在相同处理节点的不同分区以及不同处理节点内的分区中执行。处理节点之间通过AFDX交换机进行互连,所以在不同处理节点之间进行任务调度需要考虑经过交换机的时延Zi,j,计算公式定义如下:

(4)

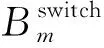
综上,任务集K的调度任务集合由分区i调度到分区j进行处理的数据传输延迟可以用以下公式表示:

(5)

2 航电系统多分区任务分配问题建模

航电系统多分区任务分配问题,可以描述为任务集合G在分区集合P上的一个映射问题,即

G→P

(6)

其在分配过程中需要考虑资源、实时性等约束,本文将其建模为多约束优化问题。

2.1 IMA系统任务分配约束

不同的任务有不同的功能资源需求,需要利用有限的资源,为运行在IMA系统上不同优先级的任务提供资源保证。因此,任务分配具有很多的约束条件。

2.1.1 实时性约束

任务集中每个任务都有实时性要求,即要求所有任务的完成时间不超过该任务截止时间。该约束可以描述为

CTi,j≤GDi,j

(7)

(8)

(9)

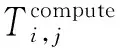
2.1.2 内存约束

由于各个分区的内存有限,需要保证分配到同一个分区的任务内存之和不超过分区的内存资源:

(10)

式中:nGi表示任务集i中任务的个数;Ψi,k,j取值为1或者0,表示任务τi,k是否分配到分区j。

2.1.3 唯一性约束

在同一时刻,只能按照任务集中的执行顺序调度一个或者多个任务,保证在数据传输过程中类似数据冲突等影响安全性的事件不会发生。因此,唯一性约束可描述为

(11)

2.2 优化目标

为了确保有效利用有限的计算资源、内存资源,以进一步优化系统任务的分配调度,这里定义了平均完成时间、均衡分区负载两个优化目标。

2.2.1 平均完成时间

通过联合优化任务分配,使系统内任务集平均完成时间最小化。具体而言,平均完成时间(Average Completion Time,ACT)的公式可以描述如下:

(12)

GCTi=max(tloc,i,tnloc,i)

(13)

(14)

(15)

式中:hp(i)为分区内优先级高于任务集i的任务集集合;tloc,i为任务集i的本地任务完成时间;tnloc,i为任务集i调度到分区j内的任务集合完成时间。

2.2.2 均衡分区负载

均衡各个处理节点内分区负载有助于提高任务的执行速度,使用标准差来衡量每个处理节点内分区荷载的离散程度。因此,HB计算公式为

(16)

(17)

(18)

(19)

(20)

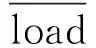
综上,该问题的优化目标函数为

min(λ1·ACT+λ2·HB),λ1+λ2=1

(21)

3 基于DDPG算法的IMA任务分配

引入基于IMA系统状态信息输入的、具有连续动作输出的深度强化学习来优化系统任务分配问题,提高系统执行效率。DDPG算法采用了深度Q网络(Deep Q-Network,DQN)的思想和基于Actor-Critic(AC)的算法结构,弥补了DQN算法不能处理连续动作空间问题的缺点[12],具有较好的收敛能力、较强的训练能力以及优秀的稳定性[13]。DDPG是深度强化学习的方法之一,其基于深度学习的部分,通过神经网络拟合泛化网络参数;其基于强化学习的部分,通过策略梯度算法使得智能体根据学习经验选择最优或较优的策略,并确定性地选择动作。

3.1 DDPG算法原理

DDPG算法分为Actor-Critic网络、IMA系统模型、奖励函数等部分[14]。本文中将IMA系统的观察信息,即IMA系统内处理节点、分区、任务集状态共同组合成该时刻的状态信息st输入至神经网络。Actor-Critic网络根据IMA系统此时状态向IMA系统提供相应的动作at,IMA系统执行该动作与环境交互,根据任务分配完成得到的下一个状态si+1获得奖励。IMA系统的目标是通过学习最优策略π:S→A,来最大化累计回报奖励Rt。同时为了提高对于系统环境的探索能力,通过添加行为噪声Ni引导算法学习新的策略,一般设定行为噪声服从高斯分布[15]。综上,DDPG算法框架如图2所示。

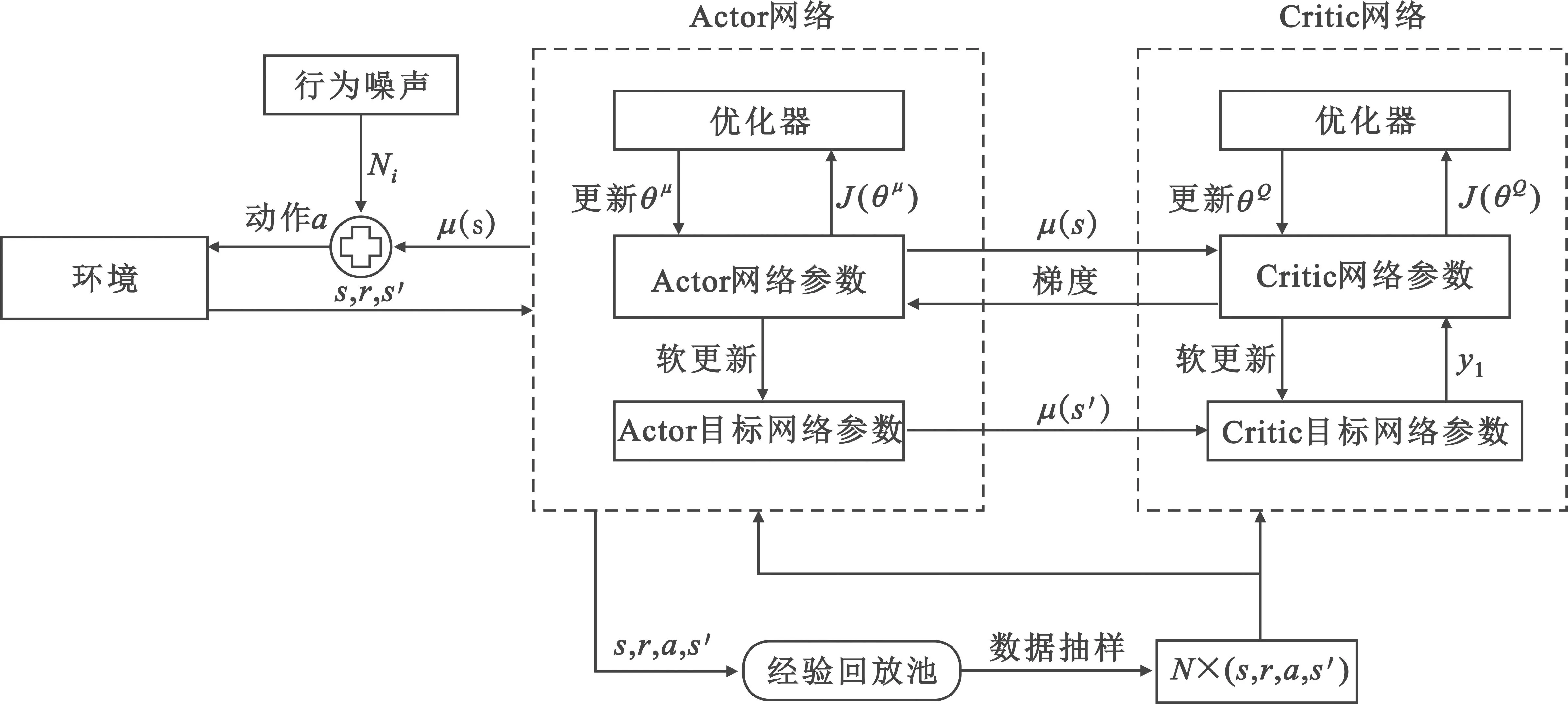
图2 DDPG算法框架Fig.2 DDPG algorithm framework

3.2 Actor-Critic网络

Actor-Critic网络具有值函数、策略函数更新方式的优点[16]。其中,Critic网络根据值函数单步更新,评价IMA系统当前分配策略好坏,网络参数为θQ;Actor网络基于当前系统状态确定性输出任务分配策略,网络参数为θμ。

同时Actor-Critic网络各自细分为评估神经网络与目标神经网络两部分。为了减少更新目标扰动带来的神经网络更新困难,评估神经网络与目标神经网络之间通过软更新(soft update)方式传参[16],公式如下所示:

θμ′←τθμ+(1-τ)θμ′

(22)

θQ′←τθQ+(1-τ)θμ′

(23)

式中:τ为滑动平均系数,一般取0.01保证更新平缓;θμ和θQ为Actor-Critic评估神经网络参数;θμ′和θQ′为Actor-Critic目标神经网络参数。

Critic网络使用全连接神经网络拟合每一个状态动作值[17],评估神经网络通过输入系统状态与采取的动作,输出状态-动作对的Q值,表示对该动作策略的评价;目标神经网络的输入来自Actor目标神经网络生成的下一时刻动作,输出下一步状态-动作对的Q值。Critic评估神经网络Q(s,a|θQ)可以更新如下:

(24)

Actor网络确定性地将状态st映射到动作at,即基于当前系统状态给出任务分配的确定性动作策略[18]。Actor评估神经网络根据Critic网络给出的Q值,通过梯度上升指导网络参数向更高评价方向更新,如下式所示:

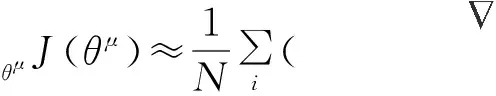
(25)

3.3 状态空间

状态空间S中包含了当前环境可以观察到的全部或部分信息,并根据观察到的信息来选择动作。为了实现对任务分配的优化,需要获取的状态信息为系统内任务集的完成时间、系统内分区待处理任务负载之和以及系统内分区剩余内存资源。因此,状态空间S表示为

S={Et,1,Et,2,…,Et,nG,El,1,El,2,…,El,nP,Erm,1,Erm,2,…,Erm,nP}

(26)

3.4 动作空间

智能体根据系统状态和观察的环境信息,选择待分配的任务集、分配的任务个数以及分配到处理节点中分区的序号,动作空间a表示为

a={Dg_task,Dnumber,Dpart}

(27)

3.5 奖励函数

设置合适的奖励函数可以引导算法学习到更好的策略,提高收敛的速度[19]。本文的研究目的是优化任务分配方案,使得系统运行更加高效,减少系统运行时间以及均衡负载,同时在分配过程中满足系统内约束条件。因此,奖励函数定义为

(28)

式中分别表示了三种状态:第一,存在分区不满足内存资源约束,则对这次分配给予超出内存资源的负奖励;第二,存在任务超出完成时限,则对这次分配给予超出时限的负奖励;第三,在满足约束的情况下,最小化平均完成时间及负载均衡,基于优化指标权重对ACT和HB之和取负值作为奖励。

3.6 状态归一化

在神经网络的训练过程中,每一层的输入都会随着前一层参数的变化而变化,这就对参数初始化以及学习率的选择有更高的要求。在IMA系统环境中,Et,1,…,Et,nG,El,1,…,El,nP,Erm,1,…,Erm,nP属于不同的序列,可能导致训练中出现问题。所以,使用一种状态归一化算法对状态观测信息做预处理,防止问题出现[20]。在状态归一化算法中,使用3个尺度因子,分别为γt(缩放系统任务集完成时间)、γl(缩放分区待处理指令条数)和γrm(缩放分区剩余内存资源[21])。算法伪代码如下:

Input:

All state variables that require to be normalized:Et,1,…,Et,nG,El,1,…,El,nP,Erm,1…,Erm,nP

Scale Factors:γt,γl,γrm

Output:

1 function StateNormalization(Et,1,…,Et,nG,El,1,…,El,nP,Erm,1…,Erm,nP)

6 end function

7S′= StateNormalization(Et,1,…,Et,nG,El,1,…,El,nP,Erm,1…,Erm,nP)

8 returnS′

4 仿真实验

系统硬件环境为CPUi12-12600KF,内存32 GB,显卡AMD 5700XT;软件环境为Windows10。实验旨在分析DDPG算法对IMA系统任务分配能力的优化,测试不同指标权重和不同算法参数对仿真效果的影响。同时引入不同环境和方案进行对比,分析DDPG算法的收敛性能和算法效率。算法部分伪代码如下:

Input:

Training episode length E,Training sample lengthL;

Actor learning rateαActor,Critic learning rateαCritic;

Discount factorγ,soft update factorτ

Experience replay bufferEpool,least batch size batchmin

Gaussian noiseNi

1 Randomly initialize the weights of actor networkθμand critic networkθQ

2 Initialize the target network with weightsθμ←θμ′andθQ←θQ′

3 Empty the experience replay bufferEpool

4 for each episodee=1,2,…,Edo

5 Reset simulation parameters of the IMA system and obtain initial observationsi

6 fori=1,2,…,Ldo

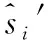
8 Get the actionaiwith actor networkθμand the gaussian noiseNi:

9 Get the rewardriand observe next statesi+1after performing actionai

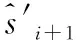
11 ifEpoolis not full then

13 else

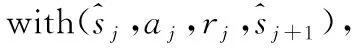
∀j=1,2,…,LfromEpool

16 Update theθQin critic network by minimizing the loss:

17 Update actor networkθμby the sampled policy gradient

18 Soft update the critic target network withτ:θμ′←τθμ+(1-τ)θμ′

19 Soft update the actor target network withτ:θQ′←τθQ+(1-τ)θQ′

20 end if

21 end for

22 end for

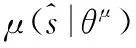
4.1 仿真实验设置

实验设定的IMA系统基本配置信息如表1和表2所示,表中τi,j为系统模型章节中任务集Gi包含的任务,j表示在任务集中的任务执行优先级。同时所有处理节点以及网络中交换机的带宽都设置为100 Mb/s,AFDX网络中交换机个数设置为1(即所有处理节点通过一个交换机互联),优化目标权重系数λ1和λ2都设置为0.5。算法初步设定训练参数如表3所示。

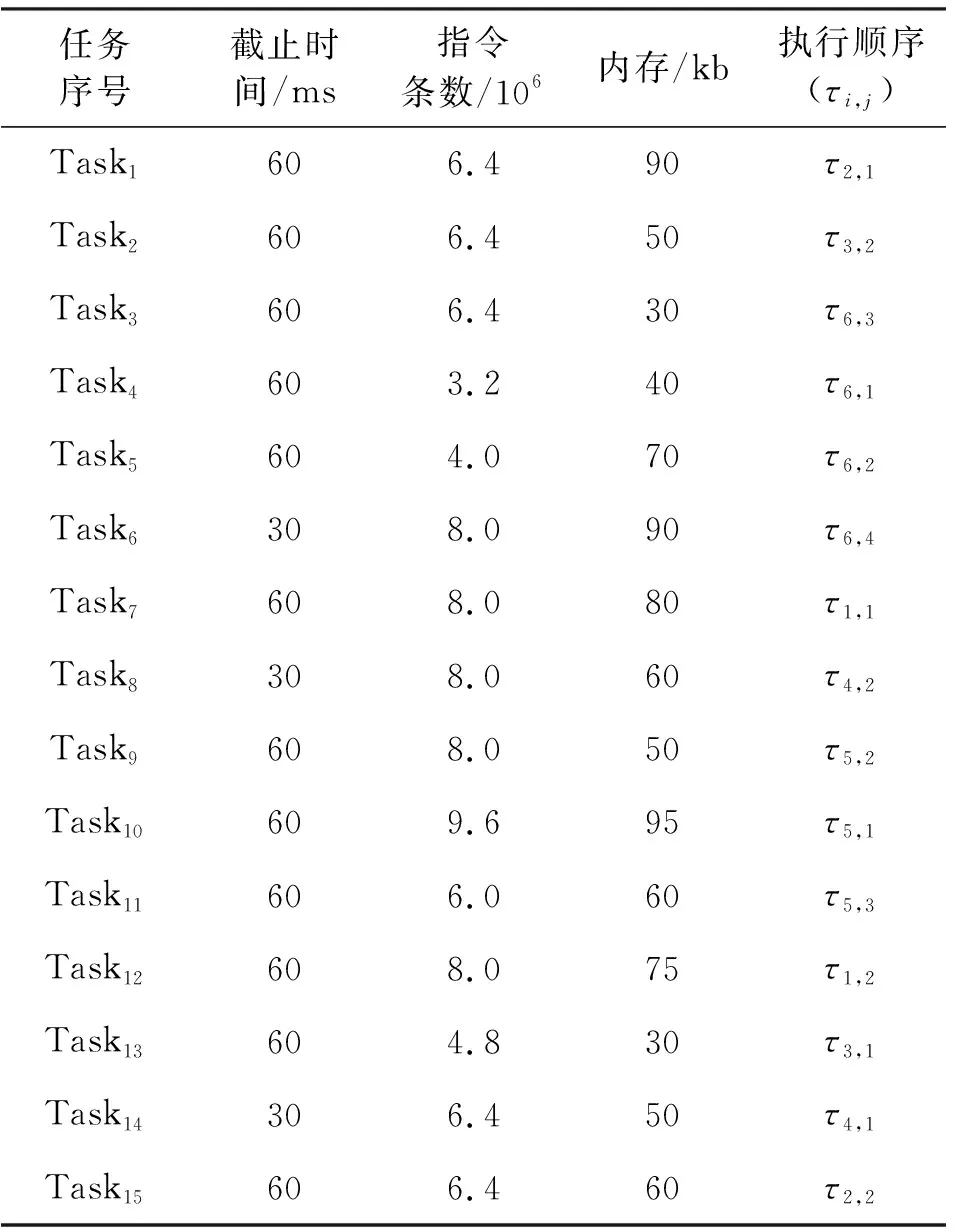
表1 系统任务属性数据Tab.1 System task attribute data

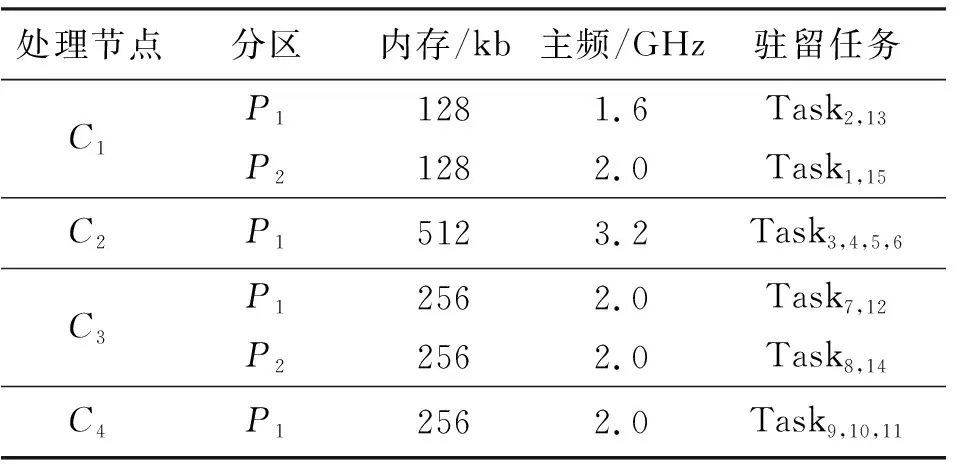
表2 IMA系统任务初始分配方案Tab.2 Initial allocation scheme of IMA system tasks

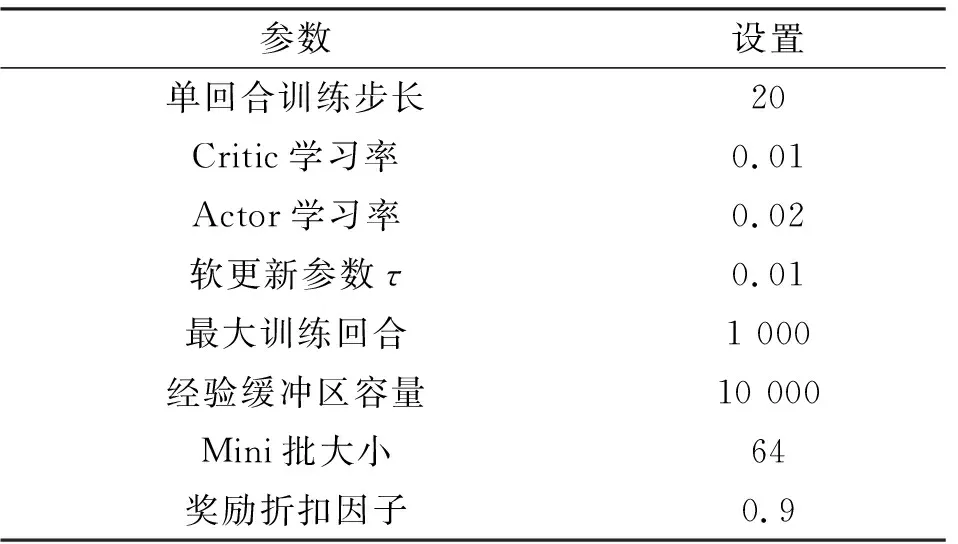
表3 DDPG算法初步设定参数Tab.3 Preliminary setting parameters of DDPG algorithm

4.2 学习率与奖励衰减分析

首先测试不同的学习率αActor和αCritic以及奖励衰减因子γ对优化训练过程的影响,确定参数的最优值用于算法的比较。在初步设定奖励衰减因子γ=0.9的情况下,取不同的学习率进行训练,结果如图3所示。

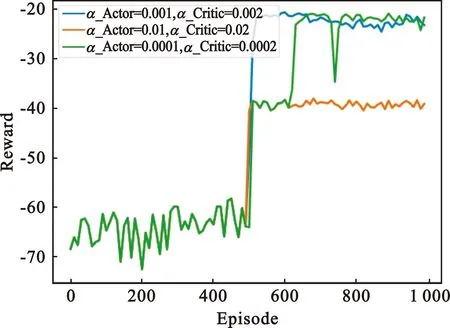
图3 不同学习率下奖励回报曲线Fig.3 Reward return curve under different learning rates

从图3可以清楚地看到,前两种情况下本文提出的算法都可以收敛,但是当αActor=0.01,αCritic=0.02时,算法收敛到局部最优解。可能的原因是当Actor网络和Critic网络拥有较大学习率时,更新步骤会更长。其次,可以发现当学习率很小时,即αActor=0.000 1,αCritic=0.000 2,算法不能稳定收敛。因此,Actor网络和Critic网络学习率最优值分别为αActor=0.001,αCritic=0.002。

在确定了学习率的情况下,比较了不同奖励衰减因子γ=0.6对算法收敛性能的影响,结果如图4所示。虽然图中曲线上升幅度相差不大,但是当奖励衰减因子γ=0.6时,训练后的任务分配策略性能最佳。γ越大,表示将整个时间段收集的数据视为长期数据,对于后续奖励的占比越大。因此,选择适当的γ值有助于提高训练后策略的性能,在接下来的实验中将奖励衰减因子设置为0.6。

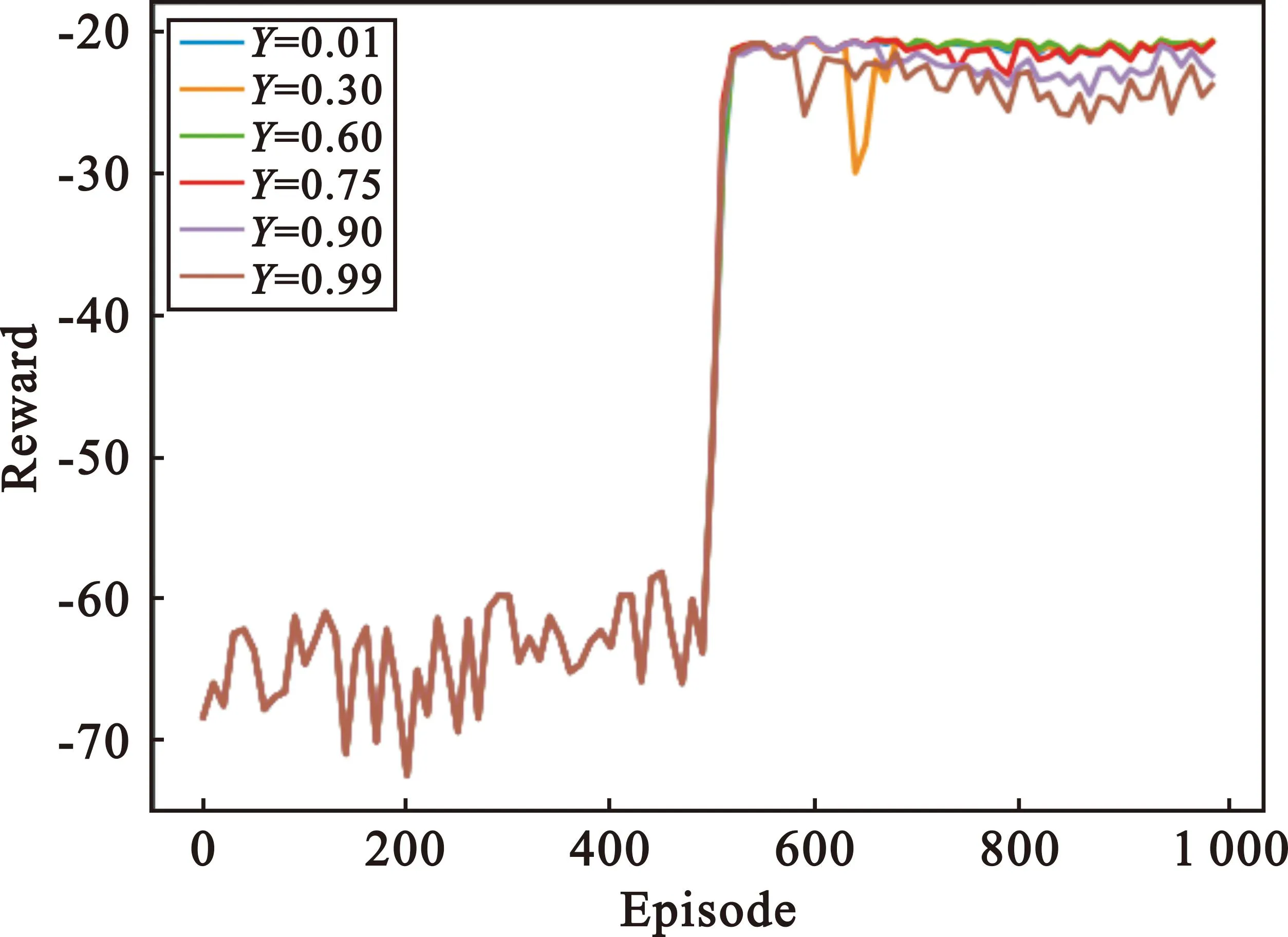
图4 不同奖励衰减因子下奖励回报曲线Fig.4 Reward return curve under different reward attenuation factors

4.3 算法性能分析

由上述分析确定DDPG算法最终参数选择如表4所示,本小节基于确定的参数将进行AC、DDPG、不带有状态归一化的DDPG、不带有行为噪声的DDPG等4种算法的比较。

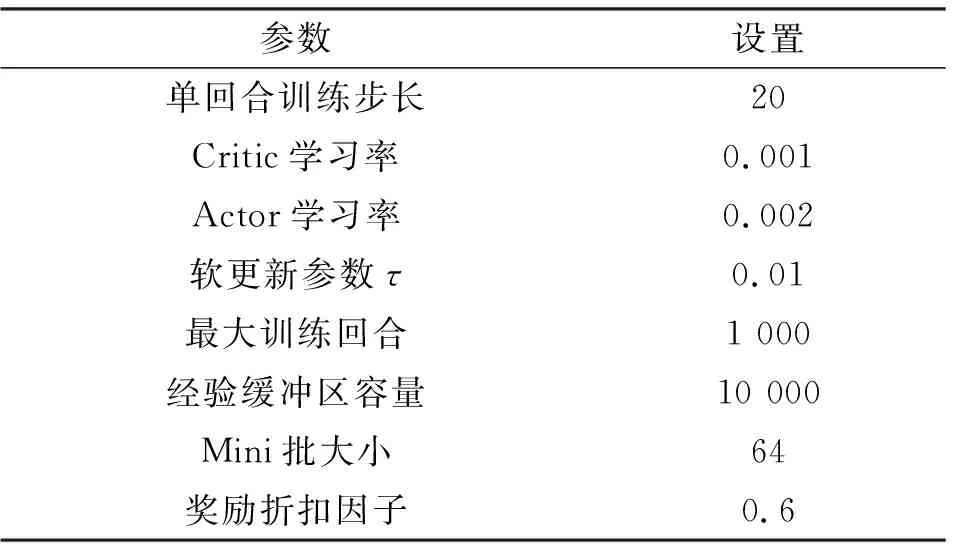
表4 DDPG算法最终设定参数Tab.4 Final setting parameters of DDPG algorithm

图5中显示了在不使用状态归一化和行为噪声的情况下,DDPG算法性能的差异。首先,可以明显发现,如果在训练策略中不使用状态归一化,训练算法将会因为状态空间内数值过大而失效。其次,如果在训练策略中没有添加行为噪声,将会导致算法收敛速度变慢以及收敛时奖励回报值更小。

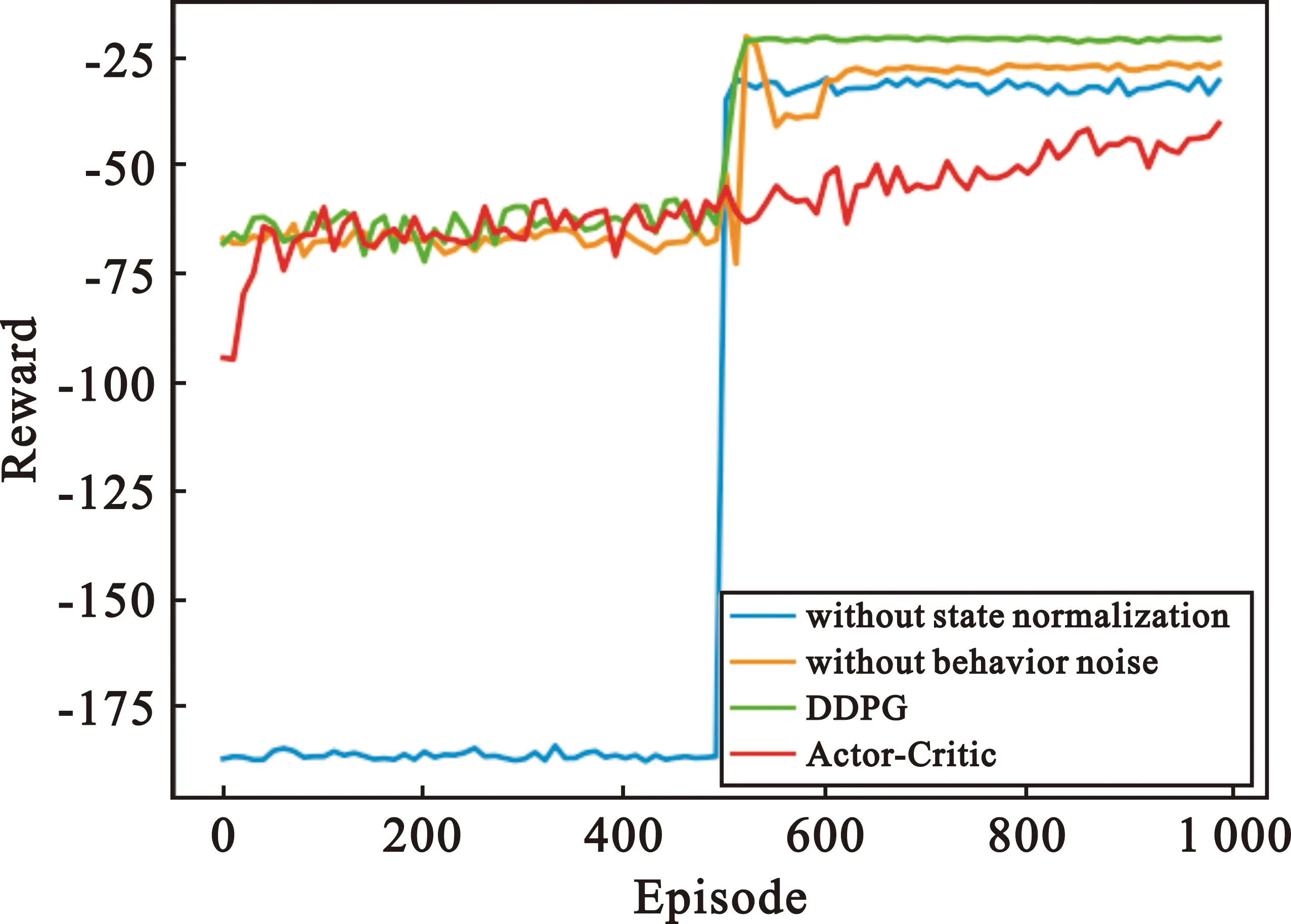
图5 不同算法下奖励回报曲线Fig.5 Task hosted in partition of processing node

随着迭代次数的增加,不使用状态归一化和行为噪声的DDPG算法以及带有两者的DDPG算法都可以收敛,但AC算法却难以收敛。这是因为AC算法的Actor网络和Critic网络同时更新,而Critic网络本身难以收敛。相比之下,DDPG受益于评价网络和目标网络的双网络结构,可以减少数据之间的相关性,从而找到最优策略。根据图5,对于相同的IMA系统环境,本文提出的DDPG算法在跳出局部最优的同时亦有最好的收敛性能。

4.4 实验结果

使用本文提出的DDPG算法进行初始环境下的IMA系统任务分配,分别提取奖励最优值和收敛值情况下的分配方案与初始方案进行对比,表5记录了从迭代第800次开始处理节点分区内驻留的任务情况。

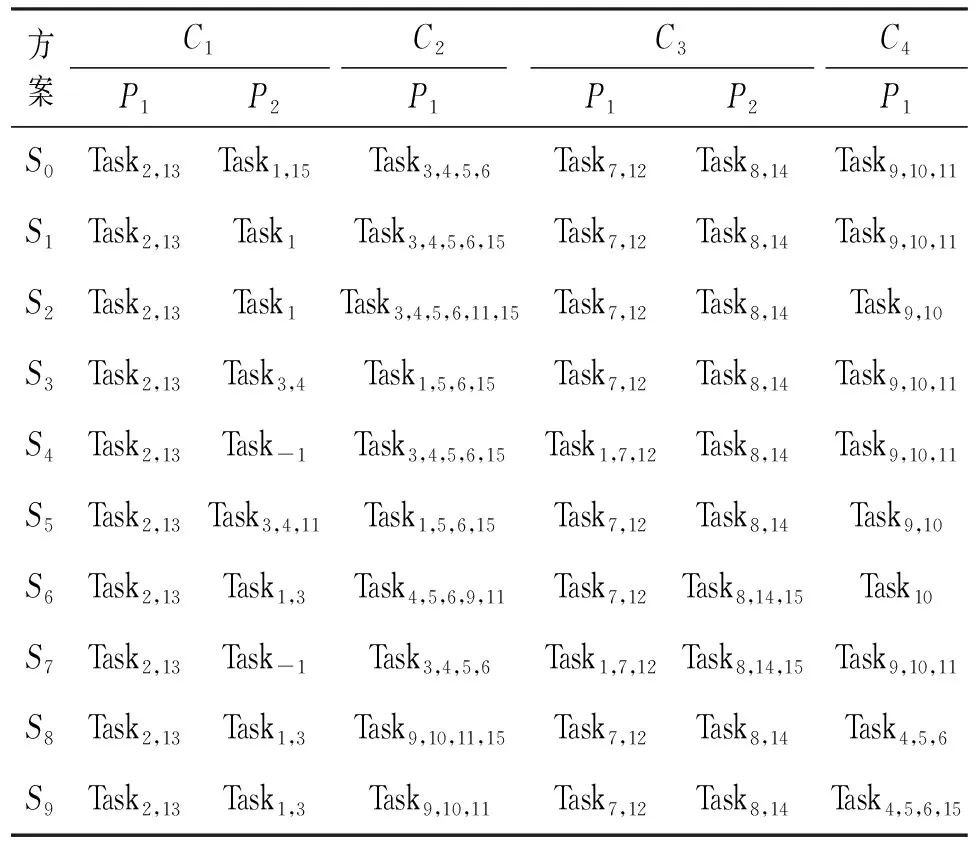
表5 处理节点分区内任务驻留情况Tab.5 Task hosted in partition of processing node

表中S1～S9任务驻留情况都满足分配约束,同时因为任务分配的唯一性约束,在训练开始时有过渡任务分配情况S1,3,4,7。以上4种情况虽然对整体系统的任务处理完成时间没有优化,但是对于故障分区C1～P2的内存资源超出情况做出修正,优化了部分系统分区的负载性能,避免影响系统运行安全的情况发生,同时也是回合奖励最优值和收敛值分配方案的中间阶段。

奖励最优值下的任务分配方案,系统运行完成时间为9.125 ms,与未使用算法优化的初始分配方案S0相比,效率提高了22.67%。奖励收敛值下的任务分配方案,系统运行完成时间为9.375 ms,与S0相比,效率提高了20.55%。

5 结束语

本文以优化IMA系统任务分配为研究对象,建立IMA系统框架,并通过DDPG算法对框架进行训练求解。在DDPG算法的基础上引入了行为噪声、状态标准化等策略训练技巧,有助于增加对于动作空间的探索以及防止出现状态空间数据过大无法计算的情况。完成了仿真实验分析,通过DDPG算法对IMA系统任务分配进行优化,得出的任务分配方案系统运行效率比初始分配方案提高了20.55%。同时与传统算法相比,收敛性能更好,效率更高。

DDPG算法涉及Actor-Critic网络,网络中参数的更新前后存在相关性,导致神经网络只能片面地看待问题。后续可以深入考虑网络参数更新机制,获得更高效的任务分配方案。