单跨铁路跨线桥预应力简支空心桥面板荷载试验★

陈文举，陈自焱，王龙胜，苏宏军，谢万友，胡 雷

(1.中铁二局集团有限公司,四川 成都 610000; 2.重庆市荣昌区交通工程建设中心,重庆 402460)

伴随着全球铁路建设的快速发展,线性交通廊道在全球范围内正在快速扩张,到21世纪中期,全球道路建设将增加2 500万km,同时伴随着铁路建设的迅速发展,公路工程与运营铁路交叉的情况日益增多[1]。

为解决这一现状,国内外学者对铁路跨线桥展开了一系列研究[2-3],马行川[4]通过从转体工艺、转体动力系统、球铰技术等方面对转体桥技术的进一步发展进行展望,提出一些解决措施和思路。陈金州等[5]在开阳高速公路改扩建工程的跨线桥改造项目中采用SPMT快速建造工法,设计了“箱形开口截面钢槽梁+钢筋混凝土桥面板”的结构型式,其效果相对较好。Zhu等[6]以火灾发生后的单跨组合钢板梁立交桥为原型,建立二元易损性曲线,得到了简支组合钢板梁跨线桥的二元结构-火灾易损性曲线。Farrag等[7]还利用移动振动台和数值模拟研究了DSSI对跨线桥动力响应的影响,研究结果表明,考虑DSSI效应的模型降低了跨线桥桥梁构件的应力水平。通过这些研究可以发现,预应力简支梁桥不仅在公路建设中得到了大量应用,在铁路跨线桥建设中也被广泛运用[8]。

桥面板作为直接承受车辆轮压的承重结构,在构造上它通常与主梁的梁肋和横隔梁(或横隔板)整体相连,既能将车辆活载传给主梁,又能构成主梁截面的组成部分,并保证了主梁的整体作用[9]。预应力简支梁桥多采用矩形板、实体连续板和空心连续板作为桥面板,然而,矩形板制作成矩形,长(宽)与厚度之比不小于1/20,其立模比较方便,施工简单,但此种板自重较大,不是很经济[10];实体连续板指板的形状为矩形(其长宽比一般为l/b≥15),板内无孔洞,即实体。它是指支承在3个支点以上的矩形实体现浇板[11];空心连续板即通常所说的矩形空心连续板,它与矩形实体连续板相似,只是板内有孔洞(即空心),根据挖孔洞率不同,可将空心连续板分成低空心率连续板、中空心率连续板和高空心率连续板不同等级[12]。

近年来,为增强桥面板的强度、耐久性及实用性等特性,国内外学者开展了大量的研究[13-14]。然而,对于铁路跨线桥很少采用预应力简支空心桥面板,更很难见到对预应力简支空心桥面板的试验结果及检测结果的分析。因此,开展预应力简支空心桥面板荷载试验是非常有必要的,本文依托单跨铁路跨线桥的实际工程,开展预应力简支空心桥面板荷载试验,并对其进行检测分析,为相关工程提供一定参考。

1 工程概况

荣昌区孙家湾跨线桥位于荣昌区广顺街道天长村孙家湾处,为一铁路跨线桥,桥型布置如图1所示。一孔13 m预应力简支空心板梁桥,桥梁全长32.45 m,该桥为农村公路便桥。桥梁设计荷载等级:人群荷载3.0 kN/m2,未考虑重型货车通行。桥面宽8.5 m,中心里程桩号为K0+112.358,预制空心板采用C40混凝土。

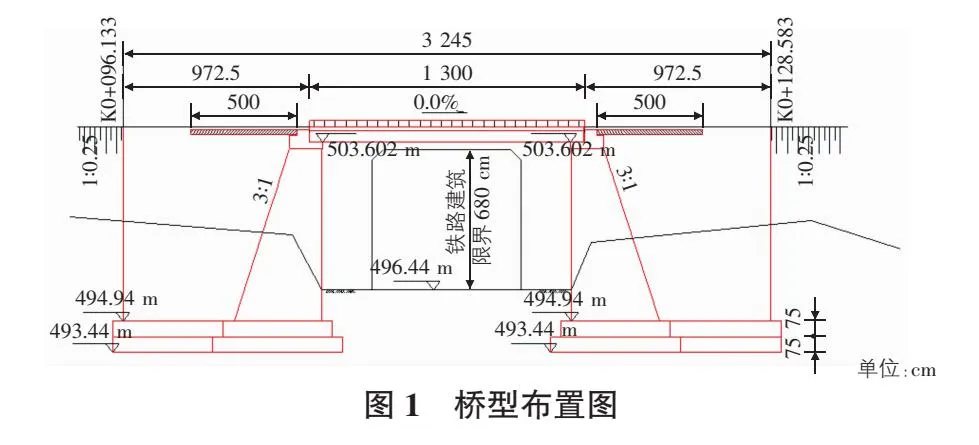
选取该桥梁预应力简支空心面板为研究对象,根据结构形式、桥梁现状及现场条件,在跨中截面布置试验测点,开展结构承载能力检算和成桥荷载试验等。

2 试验方案

2.1 结构承载能力检算

结构承载能力检算依据JTG/T J21—2011公路桥梁承载能力检测评定规程[15],以竣工资料为基础进行建模分析,并根据桥梁实际情况进行核对修正,最后通过荷载试验鉴定即可判断桥梁目前的承载能力状况。

根据相关规定[16],本文假定荷载等级为公路-Ⅱ级;或满人荷载:3.0 kN/m2。结构参数取值见表1。

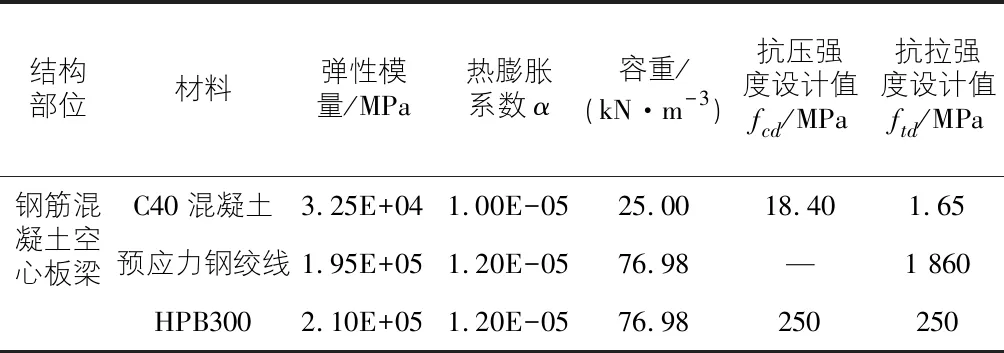
表1 材料取值参数表

桥梁结构计算采用Midas Civil 2020有限元软件,孙家湾跨线桥空心板将结构离散为19个单元,20个节点,如图2所示。

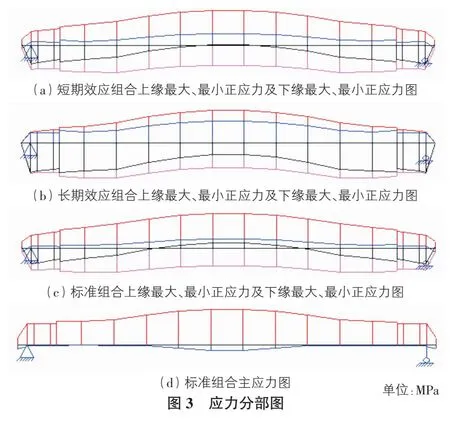
对其进行承载能力极限状态验算和正常使用极限状态验算,以抗裂验算为例,如图3所示,通过验算可知,跨线桥承载能力满足公路Ⅱ级荷载等级要求,承载能力富余量为4.8%。

2.2 成桥荷载试验

综合考虑桥梁结构特点、施工质量及桥梁现场条件,选择第1跨进行静荷载试验。本试验采用表面式电阻应变片配合相应的应变采集仪测试混凝土结构的应变;并根据现场条件,采用电子水准仪进行结构挠度测试。荷载试验前、后及过程中,跟踪观测混凝土结构表面是否存在裂缝及裂缝变化情况。

2.2.1 静载试验

本次检测为交工前荷载试验项目,以设计荷载作为控制荷载,所需加载车辆的数量及其在桥梁上的纵横向排列,将根据试验荷载产生的该加载试验项目对应的加载控制截面内力或变形的最不利效应值,按式(1)所确定的原则等效换算而得:

(1)

其中,ηq为静载试验荷载效率;Ss为静载试验荷载作用下,某一加载试验项目对应的加载控制截面内力或位移的最大计算效应值;S为控制荷载产生的同一加载控制截面内力或位移的最不利效应计算值;μ为按规范取用的冲击系数值。

本次试验加载方式分三级逐级增加到最大荷载,然后一次卸零。利用桥梁专用有限元计算分析软件MIDAS/Civil对桥梁结构进行试验设计,如图4所示。计算在公路Ⅱ级作用下各控制截面的最大内力,并根据该位置的纵向影响线,通过试验加载车进行等效加载。

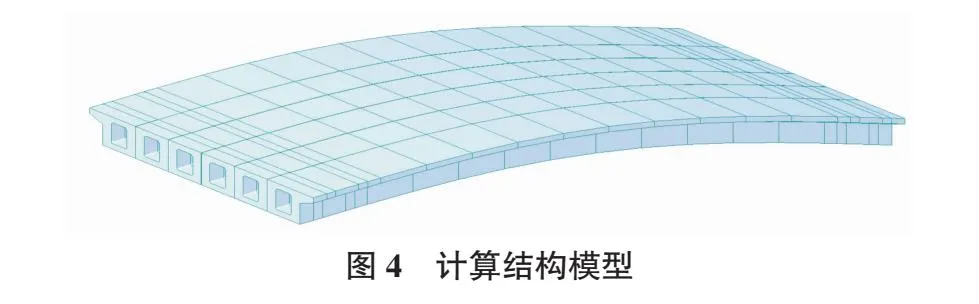
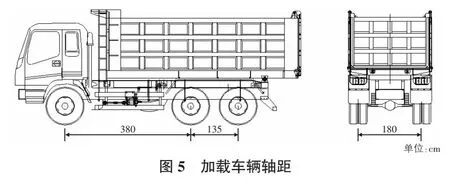
试验车辆荷载采用载重汽车加载,单辆载重汽车总重约400 kN,各车编号及轴重见表2,图5。

表2 加载车编号及轴重 kN

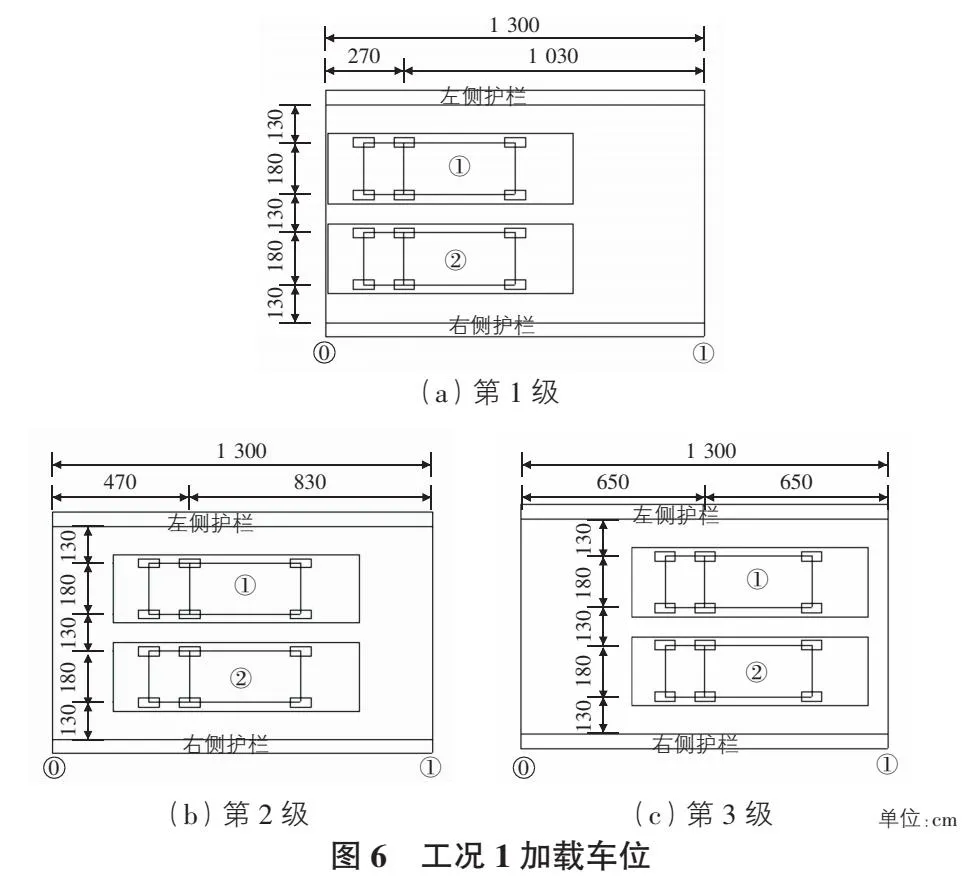
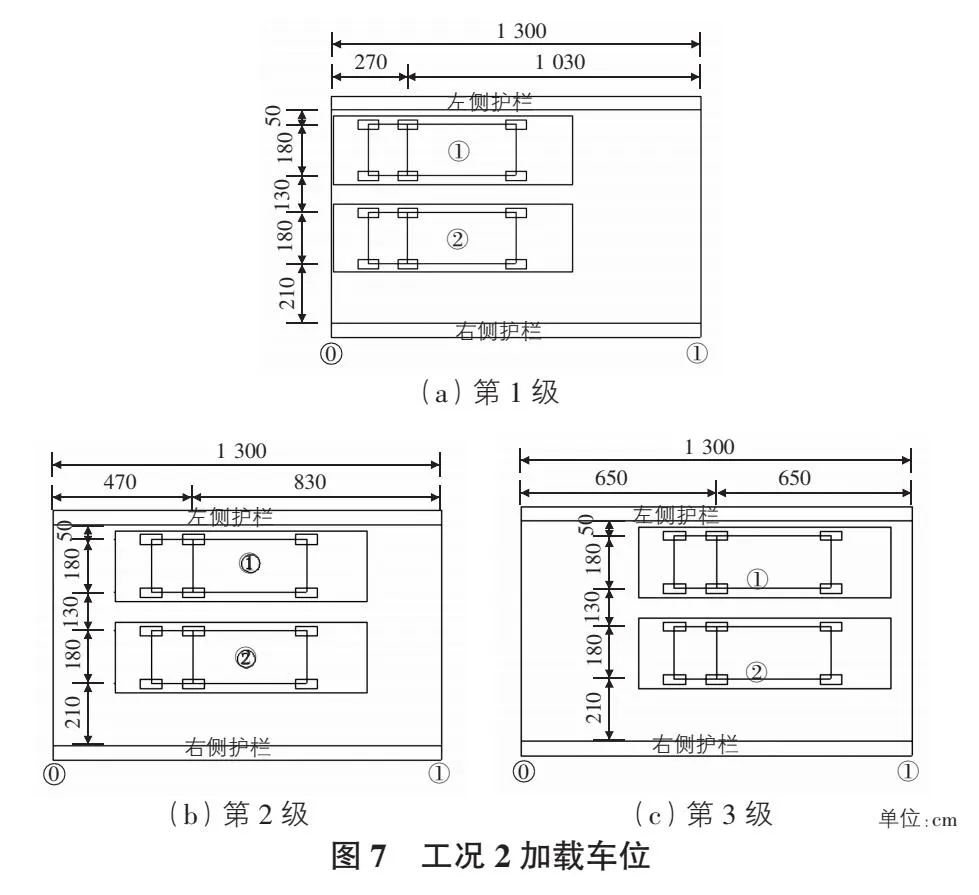
工况1、工况2分别为全桥第1跨最大正弯矩正载、偏载试验,分3级加载。各级加载内力、效率系数见表3,具体车辆布置见图6,图7。

2.2.2 动载试验

动力荷载试验是利用某种激振方法激起桥梁结构的振动,并测定其固有频率、阻尼比、振型、动力响应系数等参量,从而判断桥梁结构的整体刚度、行车性能。

本试验采用速度传感器和加速度传感器采集桥梁振动信号,经信号放大后,由动态数据采集仪进行A/D转换成数字信号,并进行数据采集和存储,在后分析计算机进行数据后处理。动态数据可实现实时采集、实时显示和初步实时分析。

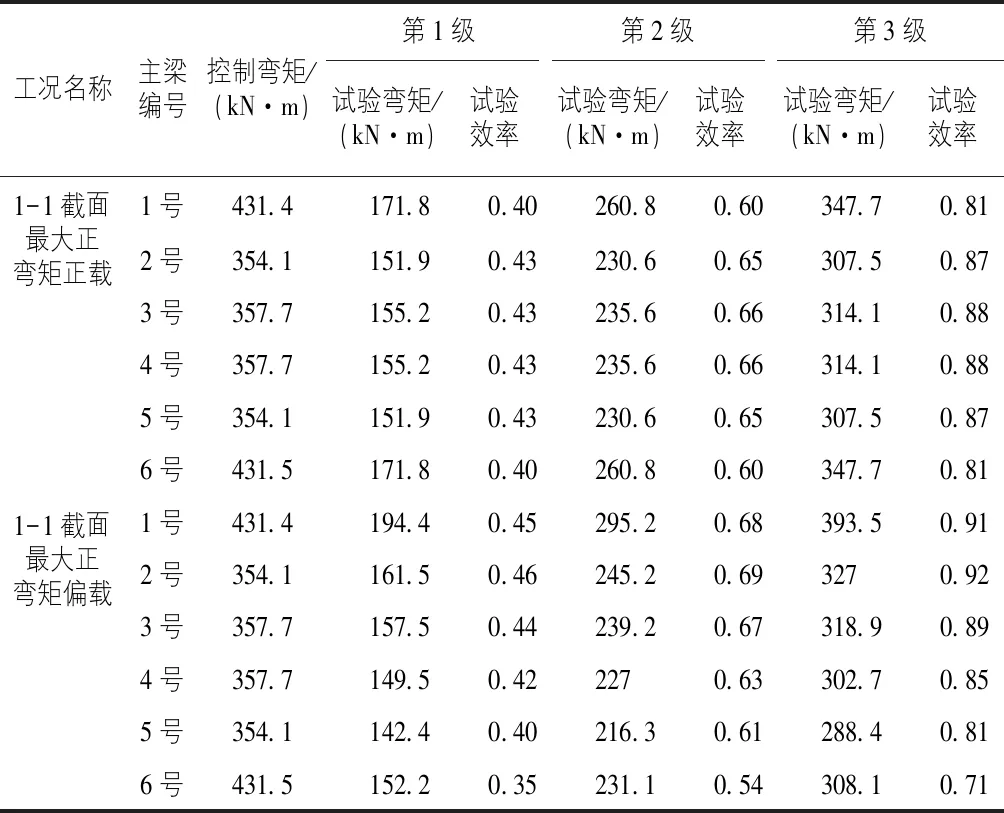
表3 两种工况第1跨最大正弯矩试验车位分级及加载效率

3 试验结果及分析

3.1 结构验算

梁桥梁荷载效应不利组合设计值应不大于结构抗力效应设计值的方程式见式(2):

γρS≤R(fd,ξcadc,ξsads)Z1(1-ξe)

(2)

确定检算系数Z1为1.13,承载能力恶化系数ξe为0.02,截面折减系数ξc为0.98,钢筋截面折减系数ξs为0.99。通过对该桥梁外观及专项检测结果分析及对其检算修正系数计算,其折减系数大于1,对承载能力计算有利,折减后承载能力满足设计及相应规范要求。

3.2 静载试验

图8(a)为工况1(第3跨跨中最大正弯矩正载)1-1截面上1号～3号测点满载挠度实测值与计算值关系曲线。图8(b)为工况2(第1跨跨中最大正弯矩偏载)1-1截面上1号～3号测点满载挠度实测值与计算值关系曲线。

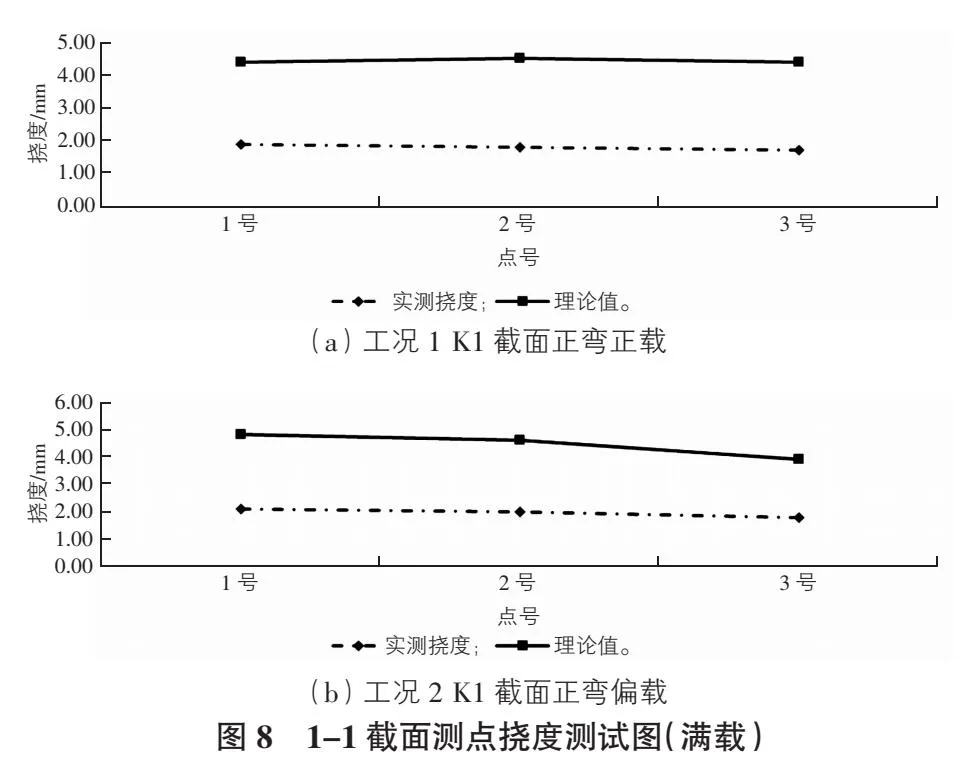
由图8可知,主要挠度测点实测值与计算值线性关系良好,且实测值小于计算值,表明结构接近弹性工作状态。由检测数据可知,工况1(第1跨跨中最大正弯矩正载)在试验荷载下,实测桥跨最大挠度为1.8 mm,主要测点挠度校验系数介于0.36～0.40之间,小于1,说明桥跨结构竖向刚度满足要求;卸载后相对残余变形在20%范围内,桥跨结构处于弹性工作状态。工况2(第1跨跨中最大正弯矩偏载)在试验荷载下,实测桥跨最大挠度为2.0 mm,主要测点挠度校验系数介于0.37～0.51之间,小于1,说明桥跨结构竖向刚度满足要求;卸载后相对残余变形在20%范围内,桥跨结构处于弹性工作状态。

图9(a)表示工况1(第1跨跨中最大正弯矩正载)1-1截面上1号～14号测点满载应变实测值与计算值关系曲线。图9(b)表示工况2(第1跨跨中最大正弯矩偏载)1-1截面上1号～14号测点满载应变实测值与计算值关系曲线。

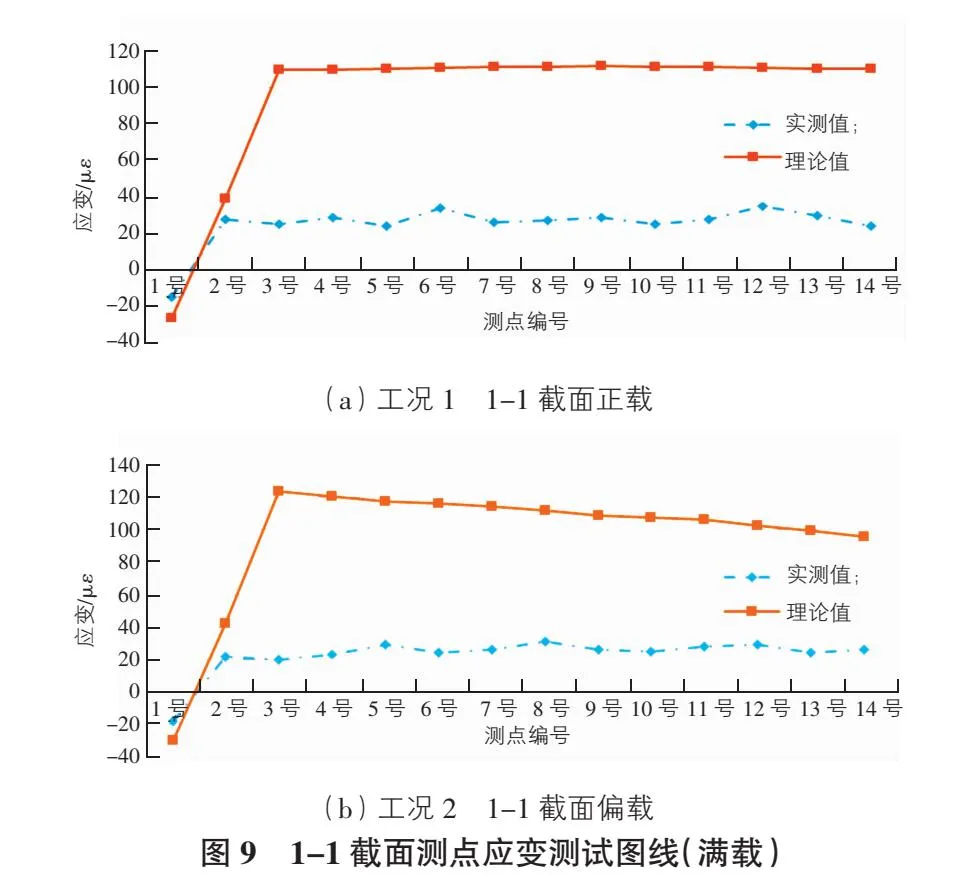
由图9可知,主要应变测点实测值与计算值线性关系良好,且实测值小于计算值,表明结构接近弹性工作状态。检测数据表明,工况1(第1跨跨中最大正弯矩正载)在试验荷载下,实测桥跨最大应变为35 με,主要测点应变校验系数介于0.22～0.74之间,小于1,说明桥跨结构强度满足要求;卸载后相对残余变形在20%范围内,桥跨结构处于弹性工作状态。工况2(第1跨最大正弯矩偏载)在试验荷载下,实测桥跨最大应变为31 με,主要测点应变校验系数介于0.18～0.60之间,小于1,说明桥跨结构强度满足要求;卸载后相对残余变形在20%范围内,桥跨结构处于弹性工作状态。

3.3 动载试验

通过对自然激励响应测得数据的辨识,以及有限元计算分析,得到结构的竖向频率为6.580 Hz,实测频谱分析结果、阻尼比分析结果、时域信号如图10,图11所示,结果汇总于表4。

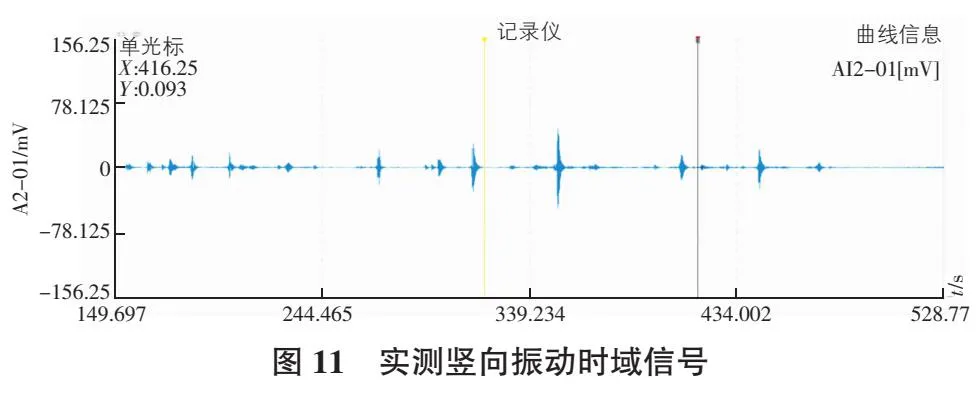
表4 结构模态参数汇总表

根据公路-Ⅱ级的通行要求,通行车辆控制上限为整车30 t、轴重12 t。结合现场踏勘可知,两端桥头均设置了限宽墩,已阻止超宽超限运输车辆通行。同时因限宽墩的存在,通行车辆在桥梁行驶速度较低,行车性能测试不具备可操作性且意义不大,本次仅做脉动试验,其评定标度作为承载能力检算系数Z1选取依据。

4 结论及建议

本文以重庆市荣昌区某单跨铁路跨线桥预应力简支空心桥为依托工程,采用两辆自卸货车进行静载实验,测定桥梁结构在试验荷载作用下的实际工作状态,评价桥梁技术状况,检验桥梁的实际承载能力是否满足设计及正常使用状况的要求,同时,建立桥面板的有限元模型,将模型的分析结果与荷载试验实测的数据相比较,以此来验证有限元模型的准确性,得到如下结论:

1)孙家湾桥所使用的单跨铁路跨线桥预应力简支空心桥面板承载能力满足公路Ⅱ级设计荷载等级要求,可以正常通车,能够很好的满足使用要求。

2)工况1～工况2试验荷载下,桥梁实测桥跨主要挠度测点校验系数介于0.36～0.51之间,均小于1,即桥跨结构竖向刚度满足要求;实测桥跨主要应变测点校验系数介于0.18～0.74之间,均小于1,即桥跨结构强度满足要求;卸载后挠度及应变相对残余均在20%范围内,即桥跨结构处于弹性工作状态。

3)为保证桥梁结构在营运期间的安全性和耐久性,建议相关部门加强对通行车辆的管理,严格按照设计荷载进行限载通行,可在桥头两侧做限重标志。