车道居中控制算法的设计与验证∗

夏钲轩 吴长水 马宏伟

（上海工程技术大学机械与汽车工程学院 上海 201620）

1 引言

车道居中控制是高级驾驶辅助系统的重要组成部分，通过环境感知、信息融合、决策控制和执行输出等环节，从而控制车辆沿着车道中心线行驶。其工作原理如下。

安装在车辆上的先进传感器（如单双目摄像头、毫米波雷达、惯导），实时感知车辆运行状态信息和车辆周围环境信息，视觉算法进行道路曲率、车辆横向偏移量、车辆相对偏航角和车道线可信度等参数计算，控制算法根据视觉算法计算结果，结合车辆运行状态等信息，进行车辆前轮转角的最优计算，执行机构控制车辆沿着车道中心线行驶［1～2］。

目前，由于高级驾驶辅助系统存在测试成本高、验证周期长、测试危险系数高等因素，多数高校仅进行了车道居中控制的模型在环测试验证研究［5］，模型在环测试存在测试参数不可调控等因素，导致模型在环测试场景覆盖度较小，无法对设计的控制算法进行更加有效的验证。针对这个问题，本文基于G29 驾驶模拟器和MicroAutoBox 实时硬件仿真系统搭建了驾驶员在环测试平台，对本文设计的车道居中控制算法进行驾驶员在环测试验证。

2 车道居中控制算法

本文以车辆的横向偏移量和相对偏航角为参考量，以车道中心线为车辆行驶的目标路径，以道路的曲率作为干扰量，基于模型预测控制原理进行车道居中控制算法的开发。车辆的横向偏移量是指，车辆的纵向中心距离车道中心线的横向距离，其中车辆纵向中心线位于车道中心线左侧时，车辆的横向偏移量为正值，车辆纵向中心线位于车道中心线右侧时，车辆的横向偏移量为负值；车辆的相对偏航角是指，车辆的行驶方向和车道中心线切线的对应夹角，其中车辆的行驶方向位于车道中心线切线左侧时，相对偏航角为正值，车辆的行驶方向位于车道中心线切线右侧时，相对偏航角为负值。车辆的横向偏移量可以控制车辆纵向中心线相距车道中心线的横向距离，但是未考虑下一时刻车辆的行驶方向，下一时刻车辆可能存在偏离车道中心线的方向行驶；车辆的相对偏航角可保证车辆下一时刻车辆的行驶方向。因此使用车辆横向偏移量和相对偏航角两个参数，可保证车辆始终沿着车道中心线行驶。

2.1 模型预测控制原理

模型预测控制原理由预测模型、滚动优化和反馈校正三部分组成。预测模型根据系统的输入信息，对将要输出的信息进行预测。滚动优化根据系统设定的目标函数，对未来时刻的控制量进行优化求解。反馈校正根据系统的实际控制效果，对下一时刻系统的理想输出重新进行规划［3］。

2.2 基于MPC车道居中控制算法

模型预测控制算法相比PID 控制算法等其他控制算法，其运算复杂度相对较高，采用较高自由度的车辆动力学模型，会增加算法的运算负担，实时性难以保证。因此，为了保证准确描述车辆动力学性能，又不增加算法负担的同时，本文采用三自由度车辆动力学模型作为模型预测控制的预测模型［4］。在三自由度车辆模型简化的基础上，建立描述车辆横向、纵向和横摆运动的三自由度车辆侧向动力学连续状态方程如下所示：

由于上述车辆侧向动力学状态方程，最终需要生成嵌入式C 代码，嵌入到智能驾驶控制器运行，因此需要对上述车辆侧向动力学连续状态方程进行离散化处理，离散化后的车辆侧向动力学状态如下所示：

上述预测模型建立好后，根据车辆横向偏移量和相对偏航角，建立如下目标优化函数：

由于车辆前轮转角机械安装位置的限制，前轮转角被限定在一定范围之内。针对这个问题，本文对控制量车辆前轮转角及其增量建立了如下约束条件：

控制量约束：

控制增量的约束：

上述目标优化函数在约束条件的限制下，可转化为二次规划求解函数：

式的前一部分反映了车道居中控制器对车道中心线的路径跟随能力，后一部分反映了车道保持辅助控制器对控制量平稳控制能力［5］。

根据上述建立的预测模型、目标优化函数和相关约束条件，结合Matlab/Simulink 自动驾驶工具箱提供的对应模块，本文搭建了车道居中控制算法模型，如图1 所示。该算法模型主要由预测模型系统、干扰量系统、参考量系统、约束常量系统和MPC优化求解系统组成。其中预测模型系统包含建立的三自由度离散化车辆侧向动力学状态方程，干扰系统包含道路曲率输入信息的处理，参考量系统包含车辆的相对偏航角和横向偏移量信息，约束常量系统包含车辆前轮转角及其增量的约束信息，MPC优化求解系统根据预测模型、车辆相对偏航角和横向偏移量反馈信息、干扰量信息和约束条件，进行车辆前轮转角的优化求解，输出车辆前轮转角参数，进而控制车辆的横向运动。

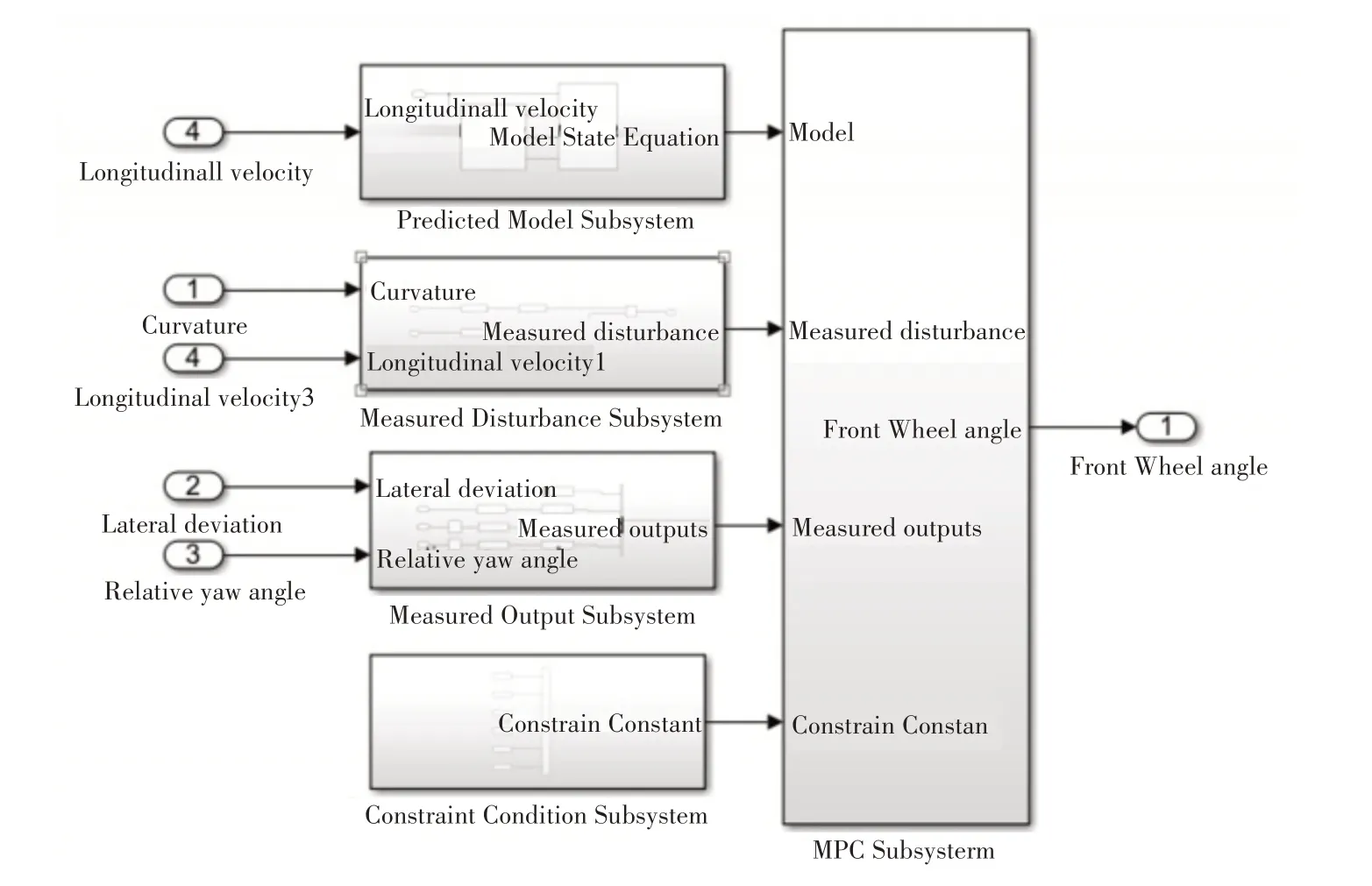
图1 车道居中控制算法模型

3 测试场景模型的搭建

根据GBT39323-2020《乘用车车道保持辅助（LKA）系统性能要求及试验方法》［6］的要求，本文在该驾驶场景设计器软件平台上，搭建了直线道路和曲线道路相连接的环形测试道路模型，其中曲线道路包括定曲率道路模型和变曲率道路模型，如图2所示。

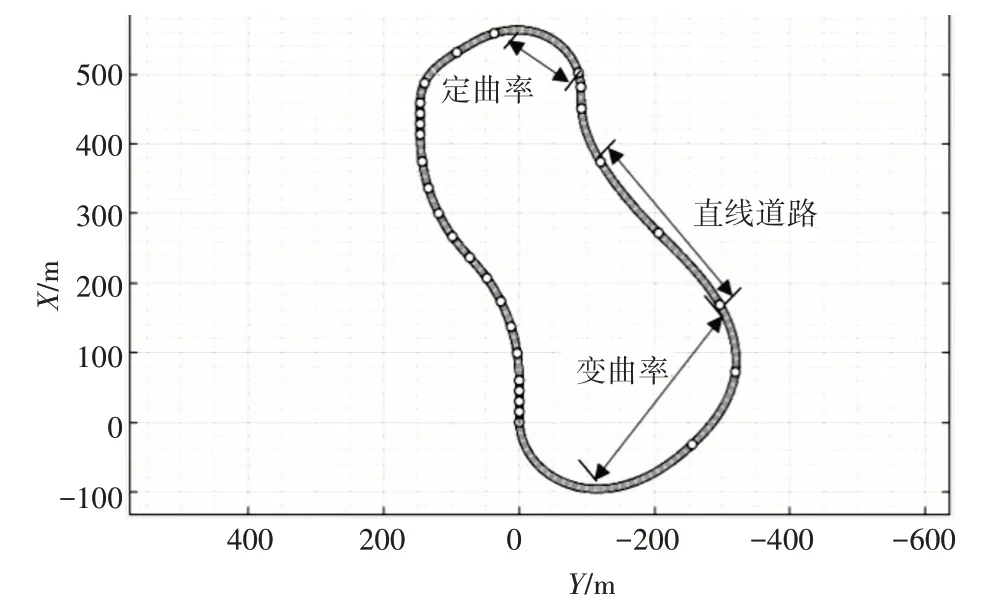
图2 测试场景模型

4 驾驶员在环测试平台

本文搭建的驾驶员在环测试平台主要由G29驾驶模拟器、MicroAutoBox 实时硬件仿真系统、服务器、直流电源和显示器五部分组成，如图3 所示。G29 驾驶模拟器主要作用是将驾驶员的前轮转角、加速踏板和转向灯等信号，输送给服务器，MicroAutoBox 实时硬件仿真系统主要运行车道居中控制算分、车辆模型和UDP 通信模型，服务器主要运行G29驾驶模拟器驱动模型、UDP通信模型和测试场景模型，直流电源主要用于向MicroAutoBox实时硬件仿真系统提供直流电源，显示器用于显示测试场景模型的3D引擎。

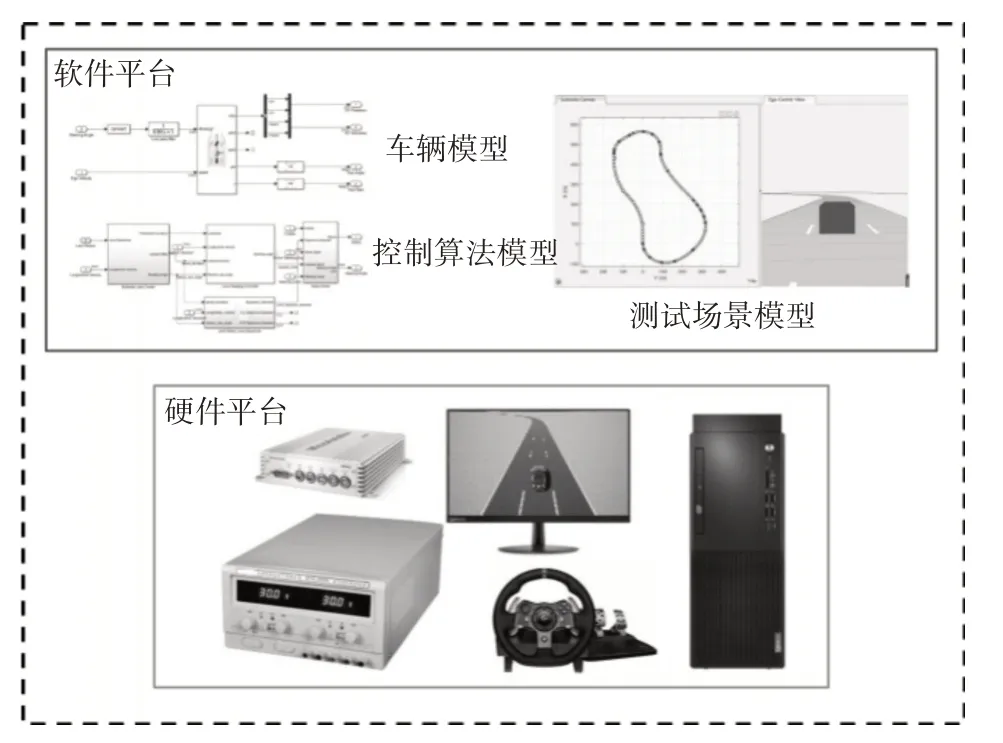
图3 驾驶员在环测试平台组成

驾驶员在环测试平台之间的数据交互主要包括两部分，一部分是G29驾驶模拟器和服务器之间的USB 接口数据交互，另外一部分是服务器和MicroAutoBox 实时硬件仿真系统之间的以太网接口的UDP数据通信。

由于Matlab/Simulink 中G29 驾驶模拟器驱动模块，提供输出接口参数取值范围为-1～1，因此需要将G29 驱动模块输出的信号量转化为实际的物理量，本文采用以脚本语言的方式，实现输出信号向物理量的转化。服务器和MicroAutoBox 实时硬件仿真系统之间的以太网接口具有.sdf描述文件下载功能，还具有服务器和MicroAutoBox实时硬件仿真系统数据传输功能。两者之间的数据交互方式主要是通过UDP 进行数据收发，其中服务器端UDP 通信以Matlab/Simulink 模块实现，MicroAuto-Box 实时硬件仿真系统端UDP 通信，需要将在ControlDesk 搭建好的UDP 通信模型、车辆模型和车道居中控制算法模型，编译成.sdf 的描述文件烧录到MicroAutoBox 实时硬件仿真系统，并且服务器和MicroAutoBox实时硬件仿真系统的IP地址要匹配，否则无法进行可靠的数据通信。

5 测试验证

5.1 测试要求

1）车道居中控制功能应控制车辆保持在车道内行驶，不应超过车道线外侧［6］。

2）车辆行驶稳定对后，驾驶员不对车辆的转向进行干预。

5.2 直线工况测试验证

驾驶员通过操作G29 驾驶模拟器的方向盘和加速踏板，控制车辆在搭建的道路测试场景上行驶，在车辆行驶稳定后，驾驶员将车辆的前轮转角控制权交给车道居中控制器，车辆的横向控制完全由车道居中控制器决定，车辆在直线道路行驶过程中，车辆的行驶路径（X 坐标表示车辆在世界坐标系下的纵向位置、Y 坐标表示车辆在世界坐标系下的横向位置）、车速、前轮转角、相对偏航角和横向偏移量变化趋势，如图4～6所示。

图4 直线工况下车辆行驶路径

由图5 可知，车辆在直线测试场景道路上行驶时，车辆的行驶速度基本保持在15m/s～21m/s，在90s～94s 期间车辆的行驶速度以较大速率进行变化。由图6 可知，车辆的前轮转角基本几乎没有发生明显的变化，表明车道居中控制算法对车辆的控制稳定性较佳。车辆的相对偏航角基本保持在参考值范围内，横向偏移量在3cm 以内，具有较好的控制精度。

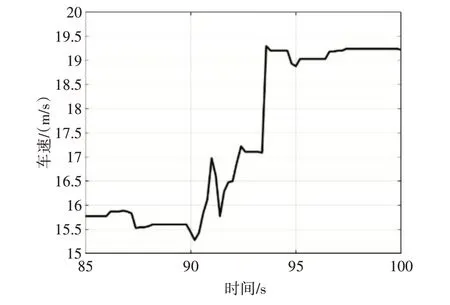
图5 直线工况下车辆行驶速度

图6 直线工况下车辆前轮转角、偏航角和横向偏移

图7 曲线工况下车辆行驶路径

5.3 曲线工况下测试验证

由图8 可知，车辆在弯道上的行驶时间大于5s，符合测试规定的要求，车辆的行驶速度保持在15m/s～21m/s 的范围变化，并且在此期间车辆以匀速运动、减速运动和加速运动三种运行状态行驶。由图9 可知，车辆的前轮转角相比直线工况下，其修正幅度具有明显的变化，特别时在车辆发生减速和加速运动时刻，车辆的前轮转角变化速率较快。车辆的相对偏航角和横向偏移量基本保持在合理的范围之内，但是车辆的横向偏移量变化幅度相对较大，在101s 左右车辆发生减速运动，车辆的横向偏移量和相对航向角发生微小的波动，在111s 左右车辆发生加速运动，此时车辆的横向偏移量变化速率较快，车辆的相对偏航角虽发生变化，但变化现象相对较小。车辆的行驶速度提高，车辆的在相同的时间内，车辆行驶的距离会更远，进而造成车辆在加速行驶过程中，车辆的横向偏移量变换幅度较大。

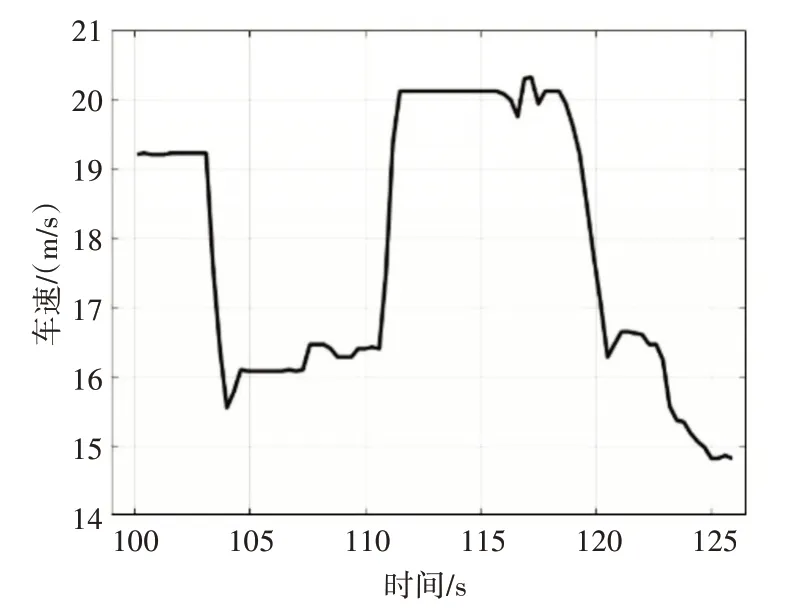
图8 曲线工况下车辆行驶速度

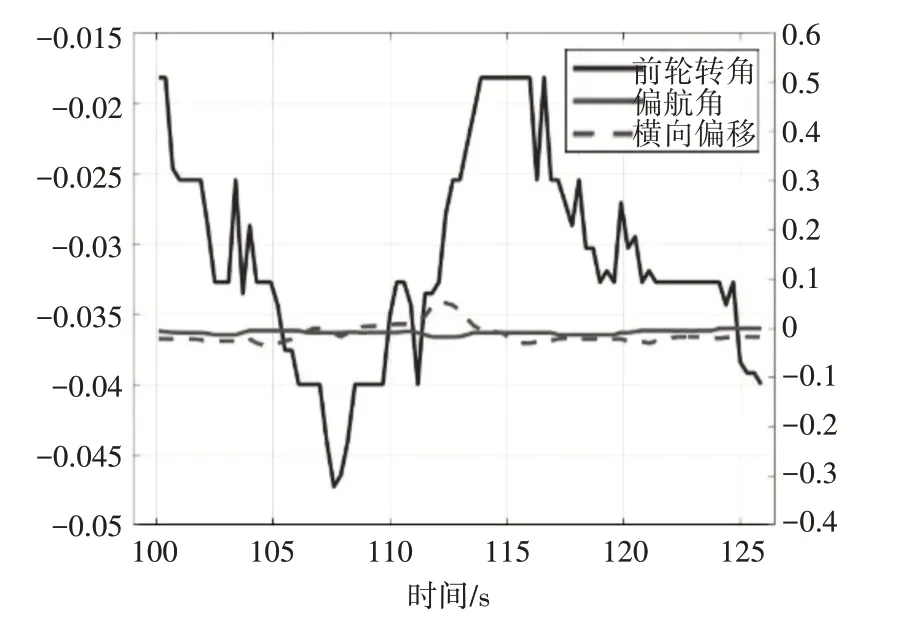
图9 曲线工况下车辆前轮转角、偏航角和横向偏移

此外，通过对直线工况和曲线工况的对比可知，在直线道路工况下，车速对车辆的横向偏移量和相对偏航角影响较小，车辆前轮转角控制稳定性也相对较佳；在曲线工况下，车速对车辆的横向偏移量和相对偏航角影响较大，车辆在发生减速或加速运动期间，车辆的相对偏航角和横向偏移量变化现象较为明显，随着车辆趋于匀速行驶，车辆的横向偏移量和相对偏航角也趋于稳定状态。相比直线工况，曲线工况下的车辆前轮转角控制稳定性较差。

6 结语

本文以车辆的横向偏移量和相对偏航角为参考量，以车道中心线为车辆跟踪目标路径，基于模型预测控制原理设计了车道居中控制算法，通过在直线道路工况和曲线道路工况下的测试，验证了车道居中控制算法的有效性和准确性。直线工况下，车速的变化对车道居中控制的影响较小；曲线工况下，车速的变化对车道居中控制的影响较大。综合来讲，道路曲率和车速的变化对车道居中控制的稳定性都有一定程度的影响。尽管本文设计的车道居中控制算法实现其基本功能，但是，本文设计的车道剧中控制算法未考虑驾驶平稳性和驾驶舒适性，下一步可将驾驶舒适性，加入车道居中控制算法，进一步完善车辆控制的稳定性。