DV-Hop 定位算法改进方法研究∗

王 勇 赵屹立

（江苏海洋大学海洋技术与测绘学院 连云港 222005）

1 引言

多年来，研究人员已经对节点定位问题提出了各种解决方案。部署过程中的每个传感器节点的位置通常由大量空间分布的传感器节点组成［1］。传感器节点随着时间的推移，他们的位置可能会改变［2］。因此，自动计算来确定传感器节点的位置成为优先选择。全球定位系统可用于准确定位，然而，它对系统硬件的要求较高，并且需要在一个昂贵的成本和功率消耗下解决定位问题［3］。所以，寻找有效的无线网络传感器定位算法成为迫切需要［4］。

DV-Hop 算法是为了避免对节点间的距离直接进行测量而提出的一种基于距离矢量路由（根据目的地远近决定最佳路径）的非测距定位算法［5］。然而DV-Hop 定位算法也存在缺点，本文就利用MIN-MAX 与最小二乘法相结合的方法对DV-Hop定位算法进行改进［6］。

2 DV-Hop算法的缺点

1）在传感器网络体系中，会存在一些bad 节点。

2）如图1 所示，节点N 可以被称为节点的位置是不唯一的，所以称该节点为bad节点。

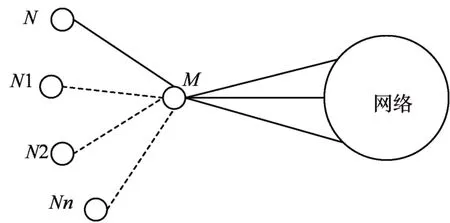
图1 第1类bad节点的示意图

3）如图2所示，节点N1只存在2个节点。不能确定E和F的位置，所以称该节点为bad节点。

4）如图3 所示，bad 节点是一个节点组。并且在节点组中没有已知的节点，该组可以绕着已知的节点坐标旋转，所以这个节点组中的所有节点都是bad节点。

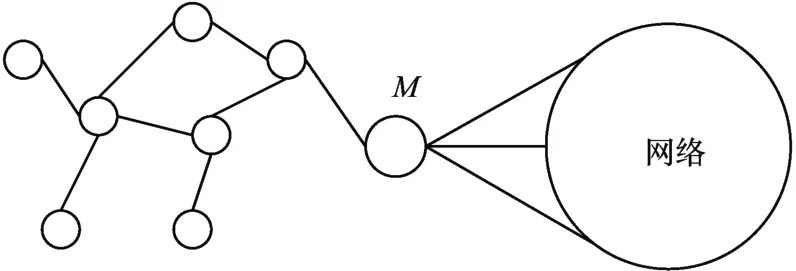
图3 第3类bad节点的示意图

5）每一个传感器节点和节点之间的距离的跳跃是已知的，与已知的节点来表示每个跳的平均距离。

6）可对该区域进行监测的范围比较小，测量节点和已知节点的接触，必须通过中间节点才能接触到。

3 DV-Hop算法的改进

传统的三边测量法计算节点的坐标会产生一些误差。MIN-MAX 算法［6］减少了浮点运算量，使计算的成本变得更小。定位精度主要由已知节点数确定，增加已知节点的数目，势必会导致成本的增加，也会增加功率消耗［7］。因此，采用MIN-MAX和最小二乘法［8］相结合的方法来取代三边测量法。

l）MIN-MAX算法

MIN-MAX算法出于协调自由分布的优化算法出现的问题，MIN-MAX 算法通过一个新的参数估计分布算法。考虑到用一种分布式的方法来解决这样的问题，提出了一种基于梯度的算法。该算法有两个显著的特点：

提出了一种分布式函数算法，使用Bregman距离。

2）提供了一种可以替代的分布式原始-对偶算法，也使用Bregman距离。

该算法的缺点是解决一类极小极大的能力分布式问题目前还没有具体的算法。但能够基本解决分布式网络结构所遇到的问题。因此，该算法可以同时解决网络定位问题。MIN-MAX算法示意图如图4所示。

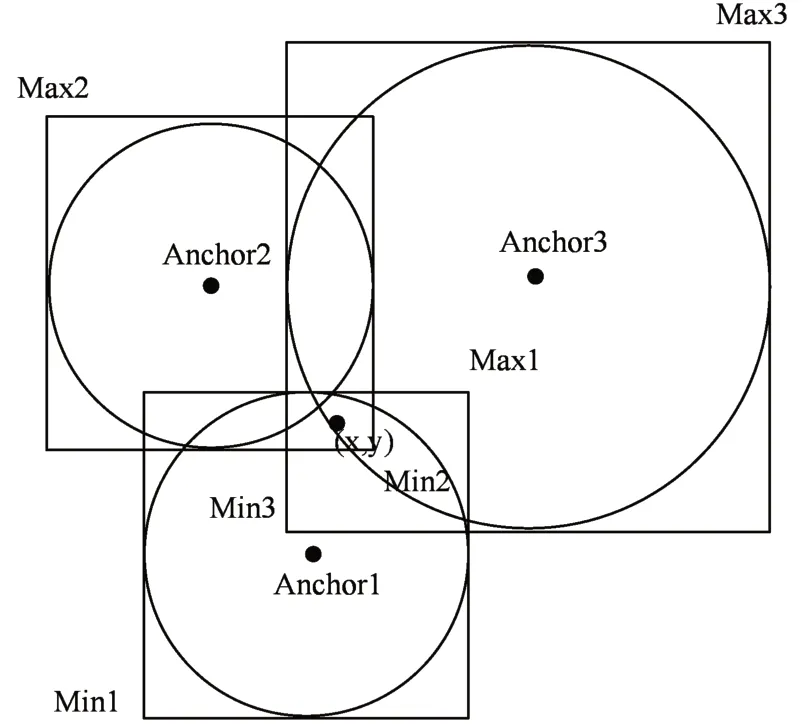
图4 MIN-MAX算法示意图

已知节点（xs，ys）的范围由［（xs-ks），（ys-ks）］*［（xs+ks），（ys+ks）］得到。交集范围可由式（1）求解出：

2）最小加权二乘法

用待测量节点到已知节点的长度估计值构造的方程ts（x），然后用式（3），求出待测节点的估计坐标［9］：

若所有的距离估计是已知的，通过构造值的加权系数ws，最小加权二乘法的估计值为

若未知节点的坐标设为（x，y），已知节点的坐标设为（xs，ys），度量的长度设为ks，则残差方程的表达式为

ts（x，y）为非线性函数，求解ts（x，y）的值，用非线性最优化来处理，求解ts（x，y）的表达式如下：

将式（6）减去式（7），得到有以下方程：

最终整理为

设有以下方程组成立：

线性处理完后，最小二乘的结果用矩阵可表示成：

最小加权二乘法的估算坐标为

只有一个对称正定矩阵可以被确定为最小方差无偏估计。在该情况下，平均误差的估计值是最小的。

在这个阶段，另已知的节点的权重是1，被测量的节点的值是在0.1的基础上，逐渐增加。

3）定位过程

过程1：这个过程是一个粗略的估计的位置。采用MIN-MAX 算法，未知节点能够通过其位置和通信模型的优点解决未知节点的距离，根据式（3）和式（4），可以估算出未知节点的坐标近似值［10］。

过程2：随着周期数的增加，未知节点的权重也在增加，节点的值逐渐接近于节点的权重［10］。一旦未知节点的权重大于1，节点坐标就非常接近。当所有的未知节点被执行时，所有的未知节点就会被定位，算法终止［11］。

4 DV-Hop算法仿真结果与分析

根据无线传感器网络的特点对参数进行设置［11］：BorderLength：边长；BeaconAmount：节点数；Sxy：存储节点的序号；Beacon：点坐标矩阵；UN：未知节点坐标矩阵；Distance：未知节点到信标节点距离矩阵；H：节点间初始跳数矩阵；X：节点估计坐标初始矩阵，X=［x，y］；R：节点的通信距离［12］。

每个节点的误差由未知节点的位置和节点位置真值之间的距离表示［13］。算法平均误差公式为

选择方案如表1所示。

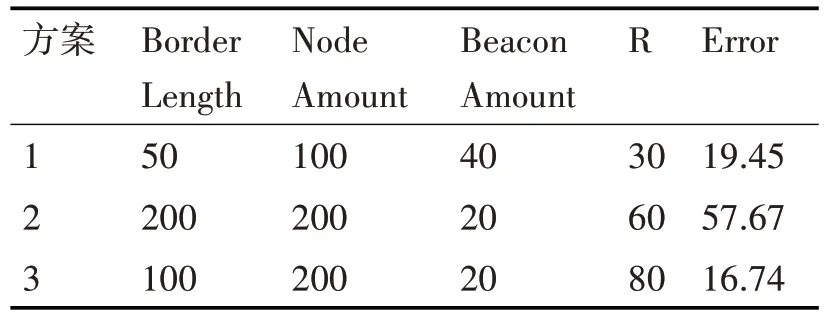
表1 定位方案

通过修改方案1 的参数，这样就可以得到一个与方案2和3对比。对比上述结果，得到如下关系：error 和borderlength 为正比例关系；和nodeamount反比关系；与beaconamount 反比关系；与R 成正比关系［14］。

从上面的比较中，我们找出了一个最佳的方案3。此时Error=16.74。仿真结果如图5、图6。

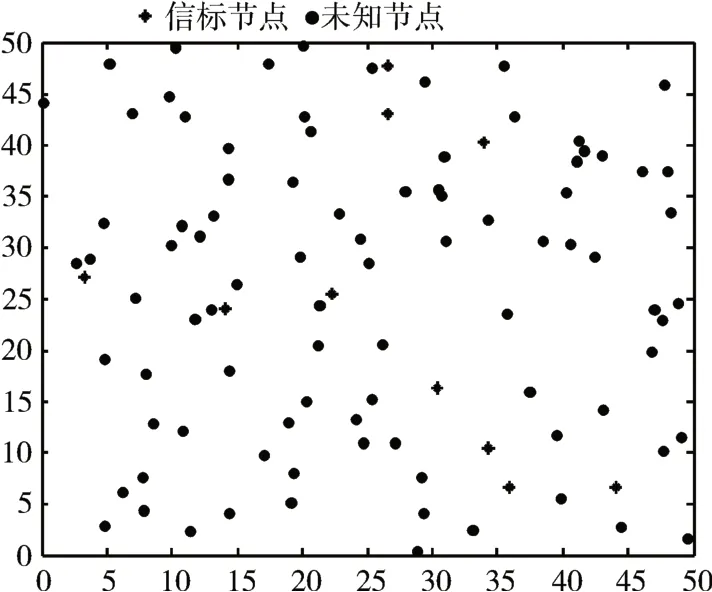
图5 方案3网络节点分布

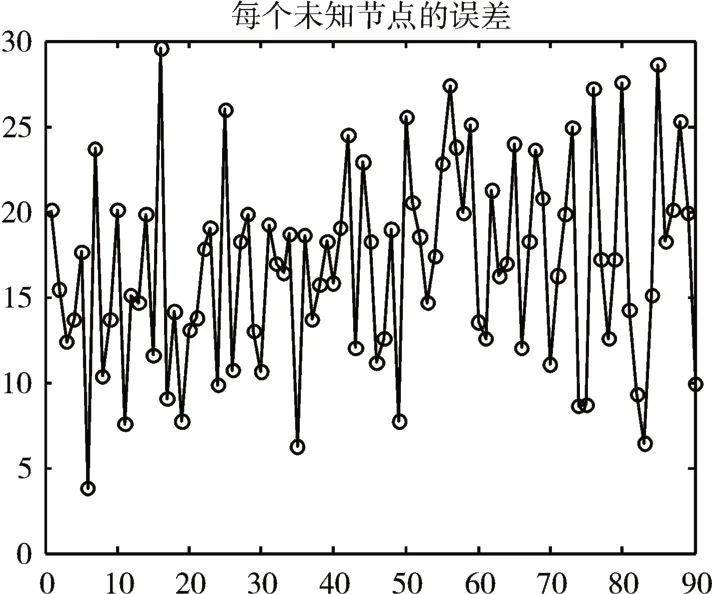
图6 方案3未知节点的误差

5 结语

本文重点介绍了DV-Hop 定位算法存在节点位置不明确的缺点，提出了以下改进：由于MIN-MAX算法能够协调自由分布的优化算法出现的问题，所以采用MIN-MAX 算法和最小加权二乘法相结合的方法替代三边测量法。通过在仿真平台对算法进行仿真实验，该算法平均定位误差Error 为16.74，表明该改进算法可以提高定位精度。