基于数学学科的STEM 课程设计

马俊海，张维忠

（浙江师范大学教育学院，浙江金华 321004）

一、问题提出

21 世纪以来，“数学教育和跨学科教育”成为国际数学教育界关注的一个重要主题①陈昊，王建磐：《21 世纪国际数学教育在关注什么——基于ICME 中TSG 主题的分析》，《数学教育学报》2020 年第2 期，第41-48 页。，数学课程综合化成为中小学数学课程改革趋势之一。2022 年4 月，我国教育部发布《义务教育课程方案（2022 年版）》和《义务教育数学课程标准（2022 年版）》，开启了核心素养导向的课程改革。在此背景下，如何实现数学课程综合化还存在诸多歧义。从文化视野出发，科学、技术、工程和数学（Science，Technology，Engineering and Mathematics，以下简称STEM）是人类文化的产物，它们在历史发展与现实应用中紧密互联。因此，当注重跨学科整合的STEM 教育与文化视野下的数学教育在课程领域不期而遇，设计一种面向数学课堂并由数学教师实施的STEM 课程，有其必要性。

1.注重跨学科整合的STEM 课程设计成为教育领域的重要主题

随着跨界与融合成为教育发展新趋势，加强跨学科内容与教学成为课程改革的重点，跨学科课程融合成为创新育人方式、促进学生核心素养提升的重要路径，这使得注重跨学科整合的STEM 课程设计成为一个研究热点。②孔晶：《基于认知深度模型的STEM 课程设计路径研究》，《现代教育技术》2021 年第9 期，第112-119 页。从历史角度看，源自美国的STEM 课程经历了多种形态，并朝着“STEM+”课程（如STEAM 课程）的趋势发展。③大卫·安德森，季娇：《从STEM 教育到STEAM 教育——大卫·安德森与季娇关于博物馆教育的对话》，《华东师范大学学报（教育科学版）》2017 年第4 期，第122-129 页，第139 页。21 世纪，美国重视STEM 课程的原因至少有三条：通过在数学和科学课程中整合技术和工程，提高学生的数学和科学成绩；以STEM 课程为媒介，为中小学工程教育提供平台，吸引更多学生进入STEM 领域；提高学生的综合能力，发展学生21 世纪技能。进入新时代，我国教育界日益认识到STEM 课程的社会价值和个人价值（如认识价值、德育价值），日益重视STEM 课程研究。

2. 面向数学课堂的STEM 课程设计是一个亟待探索的研究领域

近年来，我国对于如何设计STEM 课程开展了一些研究，开发了许多课程资源。然而，它们主要面向科学和技术课堂。①孙妍妍，何沣燊：《以“工程”为中心的STEM 课程驱动问题设计研究》，《华东师范大学学报（教育科学版）》2021 年第8 期，第33-44 页。在STEM 课程中，一个长期存在的问题是：数学只是解决科学或工程问题的一种工具。诚然，一些科学和技术教师在设计STEM 课程时将数学作为学习目标，但在教学过程中却难以引导学生深化理解数学，因为他们通常是数学的熟练使用者，但对数学的本质、数学价值观等并不熟悉。尽管研究者在STEM 课程与教学中纳入了广泛的数学内容，但聚焦数学的研究却相对较少。从学科角度来看，数学是STEM 课程的重要构成，不应成为沉默的“M”。由于数学教育工作者更容易发现学生数学能力提升的机会，故而，设计可由数学教师在数学课堂中实施的STEM 课程是一个亟待探索的新研究领域。

3. 以“STEM 整合”为抓手，有助于落实数学课程与教学中的跨学科教学活动

发展学生的数学核心素养是21 世纪国际数学教育的重要主题，也是我国数学教育面向未来发展的必要选择。数学核心素养的实现需要依托跨学科的教与学，故而，数学课程教学中跨学科和综合实践活动的落实成为一个关键问题。当前，主题式学习、项目化学习（Project-Based Learning，以下简称PBL）等已被纳入《义务教育数学课程标准（2022 年版）》，数学项目学习被视为实现数学核心素养的重要路径。但从实践角度来看，绝大多数小学和初中数学教师可能会对如何实施主题式学习、PBL 感到茫然。因而，以“STEM 整合”为抓手，从文化视野重新审视STEM 学科的关系，或可对数学教师实施跨学科活动有所启迪。

综上可知，进行面向数学课堂的STEM 课程设计有其必要性，面向数学课堂的STEM 课程涉及课程整合。鉴于基于学科的课程整合适切教育改革的生态环境，是提升学生认知能力的基础②裴晓：《论基于学科的课程整合方式》，《现代基础教育研究》2023 年第1 期，第196-202 页。，本文旨在从本体上厘定“基于数学学科的STEM 课程”，探讨其设计可行性并提出设计策略。

二、本体厘定

1. 基于数学学科的STEM 课程的内涵

基于数学学科的STEM 课程是一种文化取向的数学“综合与实践”课程，旨在通过建立数学与科学、技术或工程之间的联系来改善学生的数学学习，发展其数学核心素养。具体而言，深化理解基于数学学科的STEM 课程可进行多维透视。

（1）基于数学学科的STEM 课程是数学课程综合化的一种具现

从学科角度来看，STEM 有三重意涵，即狭义上指代科学、技术、工程和数学四个学科领域，广义上还包括心理学、社会学等社会科学，以及指代四个学科是一个紧密联系的整体。③本文对STEM 的使用，涵盖第一层、第三层含义。基于此，STEM 课程可指代“综合STEM 课程”。因此，着眼于STEM 的学科角度，基于数学学科的STEM 课程是数学课程综合化的一种具现，代表着一种思考我国数学“综合与实践”课程改革的方式。

（2）是探索数学与其他STEM 学科之间教与学的一种综合方法

在一定意义上，基于数学学科的STEM 课程是一种基于数学与现实世界问题之间的联系，将数学与一个或多个其他STEM 学科内容纳入数学课堂中的努力。基于数学学科的STEM 课程是一种通过有意识地将数学与一个或更多其他STEM 学科相关联来组织课程与教学的方式，尤其强调将工程要素和技术实践融入数学课程体系中。因此，任一STEM 学科都可在基于数学学科的STEM 课程中有学习目标，但数学和工程是主要目标。基于此，在设计基于数学学科的STEM 课程时，教师应有意识地设计数学与至少一个其他STEM 学科的学习目标，注重通过情境整合、数学建模和工程设计来教授STEM 知识，从而深化学生对数学的理解。

（3）注重数学学科系统性和STEM 学科交互性的相互统一

基于数学学科的STEM 课程具有抽象性，本文提出了两个概念模型来帮助理解其内涵。其一是一个整合工程的STEM 课程模型（见图1）。据此，基于数学学科的STEM 课程要与我国义务教育数学跨学科综合教学联系起来，既要保留数学的独特性，又要强调数学与其他STEM 学科（尤其是工程）的交互作用。该模型有两个重要假设：一是只有具备STEM 学科内容知识和综合教学知识的教师，才能使这种交互在数学课堂中真实发生；二是尽管数学和工程具有不同的认识论特征，但二者存在紧密的内在关联。这意味着中小学工程教育可发生于数学和工程学科的交叉处，学生可在整合工程的数学“综合与实践”课程中，体验工程设计过程，感受设计思维与建模思维的异同。

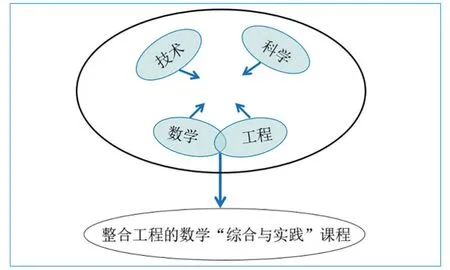
图1 聚焦数学与工程的STEM 课程模型

其二是一个基于情境学习理论、聚焦数学建模和工程设计的滑轮系统模型（见图2），它将基于数学学科的STEM 课程视为一个滑轮系统。其中，数学建模、工程设计、科学探究和技术素养是4 个滑轮，用于提升负载，即情境性STEM 学习。在这一系统中，各个滑轮都连接着常见的STEM 实践，实践共同体作为绳索将4 个滑轮与负载联系起来。因此，整个滑轮系统必须协调工作，以确保系统的完整性。尽管这一模型将数学建模、工程设计、科学探究和技术素养联系起来，但这并不意味着在设计基于数学学科的STEM 课程时，必须同时涵盖四个STEM 学科的学习目标。

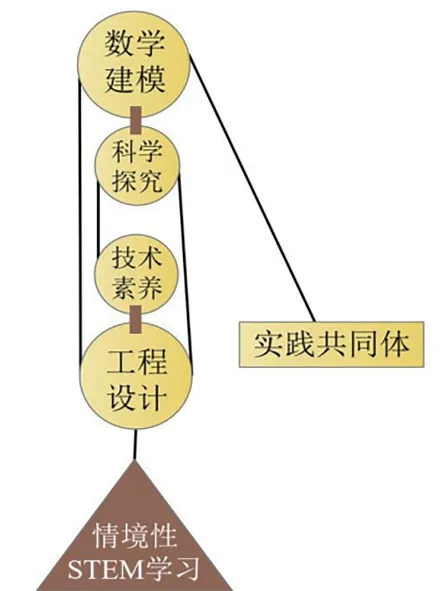
图2 滑轮系统模型

尽管两个模型各有侧重，但都聚焦STEM 中的数学和工程，强调数学建模和工程设计活动能够有意地促进学生深化理解STEM 内容和实践所必需的高阶思维。从问题解决角度来看，问题解决的数学方案与工程方案存在一致性。对于基于真实情境的开放式问题，问题解决的数学方案着重于启发式思维并强调数学建模，工程方案则着重于设计式思维并强调工程设计。然而，数学建模和工程设计都强调问题解决是一个迭代循环的过程。因此，深化理解基于数学学科的STEM 课程，要求教师关注设计师式的认知方式与数学启发式的解题方式之间的一致性，注重工程设计过程与数学建模过程的关联性。

（4）跨学科整合是基于数学学科的STEM 课程的重要内涵

理解基于数学学科的STEM 课程离不开对课程整合的讨论，课程整合的相关研究非常丰富。诸多学者的研究表明了课程整合有不同的程度和模式。①裴晓：《论基于学科的课程整合方式》，《现代基础教育研究》2023 年第1 期，第196-202 页。例如，福格蒂（Fogarty）根据整合程度不同，提出了一个课程整合的连续统一体框架，将课程整合分为具体科目整合、科际整合和学习者整合三大类，并分为分立式、联立式、巢穴式、关联式、共享式、网状式、串联式、跨科式、浸入式和网络式十种模式。②R.J. Fogarty，“Ten Ways to Integrate Curriculum”，Educational Leadership，Vol.49，no.2（1991），pp.61-65.德雷克（Drake）等学者主张，课程整合就是建立联系，并明确了多学科、跨学科和超学科三种方法。③S.M. Drake，R.C. Burns：《综合课程的开发》，廖珊，黄晶慧，潘雯译，中国轻工业出版社2007 年版，第7-16 页。因此，多学科、跨学科和超学科的范畴为理解基于数学学科的STEM 课程提供了参照，它主要涉及跨学科的范畴，并处于多学科和超学科的边缘地带。

（5）基于数学学科的STEM 课程是一种文化取向的数学课程

从文化视野出发，数学概念的创造和发展与科学、技术、工程等紧密关联，基于数学学科的STEM 课程就是一种文化取向的数学课程。在这一方面，艾伦·毕晓普（Alan Bishop）的研究为我们从文化视野来理解基于数学学科的STEM 课程提供了参考。由于数学文化是由活动发展起来的特定符号技术与数学文化中价值观的联结，所以，毕晓普主张构建一种文化取向的数学课程，并提出它应遵循“代表性、形式性、可及性、解释性、广泛而基础性”五原则，以及“基于概念的符号要素、基于项目的社会要素、基于调查的文化要素”三要素。①A. J. Bishop，Mathematical Enculturation：A Cultural Perspective on Mathematics Education，Dordrecht：Kluwer Academic Publisher，1988，pp.92-120.其中，三要素提供了一个知识框架，使文化取向的数学课程能够满足五原则。

2. 基于数学学科的STEM 课程的要素

（1）数学性

当前，大多数STEM 课程是一种项目综合体，它们多聚焦于解决一个实际问题，学生在这一过程中学习的数学知识并不系统，更体会不到数学所具备的价值观念。在常规STEM 课程中，数学主要扮演着工具性角色，因为科学和技术教师在设计STEM 课程时，通常假定学生掌握了开展科学探究或技术实践所需要的数学知识。因此，他们更多地要求学生应用数学。数学性意味着基于数学学科的STEM 课程既以数学学科知识为基础，又要帮助学生学习数学（而不只是应用数学），在价值取向上将数学的工具化转变为目的化，强调凸显数学的知识体系。

（2）数学化与生活化

数学化和生活化之间具有一定的关联性。基于数学学科的STEM 课程既要体现生活性和真实情境性，又要逐渐数学化。当学习者是低龄儿童时，教师设计基于数学学科的STEM 课程应倾向于生活化，注重实物产品的教学价值。随着儿童年龄的增长，所设计的课程要更倾向于数学化。绝对的生活化和绝对的数学化都不是基于数学学科的STEM 课程的应有之义。可以说，基于数学学科的STEM 课程旨在帮助中小学生深化理解数学世界与现实世界以及二者之间的关系，如数学源自现实世界而又超越现实世界，它也可应用于现实世界。

（3）数学成就取向

该要素意味着基于数学学科的STEM 课程是要帮助学生取得数学成就，包括改善学生的数学情感、数学态度、数学信念、数学价值观、数学能力（如数学建模能力）等。从学科德育角度来看，这也表明基于数学学科的STEM 课程能发挥数学育人价值，帮助学生逐步社会化，成为有理想、有本领、有担当的时代新人。事实上，相较于考试成绩的提升，数学成就取向更多地体现在帮助学生认识到数学与其他STEM 学科、数学与生活的紧密关联性，促进学生形成正确的数学观和数学学习观，减少学生学习数学时的恐惧、焦虑和厌恶。

3. 基于数学学科的STEM 课程的特征

基于数学学科的STEM 课程具有四大特征。第一，以数学学科知识为基础，体现数学的社会文化性。这一关键特征意味着基于数学学科的STEM 课程注重向学生传递数学文化价值观。它在体现数学的社会文化性时，也体现了数学的技术性、工具性和艺术性。第二，以探寻知识关联性为主旨，将数学与科学、技术或工程相整合。跨学科整合是STEM 教育最重要的特征②余胜泉，胡翔：《STEM 教育理念与跨学科整合模式》，《开放教育研究》2015 年第4 期，第13-22 页。，STEM 课程表现为整合两个或更多STEM 学科，基于数学学科的STEM 课程的一大特征是探寻STEM 学科知识的关联性，将数学与一个或多个其他STEM 学科相整合。第三，以数学史与数学文化为桥梁，体现基于模型和设计的活动。常规STEM 课程注重探究、项目及问题的设计③S.C. Fan，K.C. Yu，K. Y. Lin，“A Framework for Implementing an Engineering-Focused STEM Curriculum”，International Journal of Science and Mathematics Education，Vol.19，no.8（2021），pp.1523-1541.，基于数学学科的STEM 课程注重数学史和数学文化的价值，更倡导基于模型或设计的活动。在历史上，普遍性的设计活动促使不同文化的人们创造出自己的数学。第四，以“深化学习”为目的，体现基础性及提升学生的数学核心素养水平。这意味着它要适用于大多数学生。此外，基于数学学科的STEM 课程也具有一些常规特征，包括体现情境性、开放性、趣味性和挑战性，有一个激励师生成为积极学习者的环境。

4. 基于数学学科的STEM 课程的类型

基于数学学科的STEM 课程的常见类型有数-科整合、数-技整合、数-工整合及珠-线整合模式。设计基于数学学科的STEM 课程必然会加重教师的工作负担，全盘跟进各类型既无必要也无可能，因而，应找出最适切我国数学课程发展需求的类型。

（1）数-科整合最易被教师在观念上所接受

设计数-科整合课程有大量的理论基础和实践案例，但它并不是最符合我国数学课程发展需求的类型。当前，数学和科学是学校课程体系的重要构成，在数学课程中过多融入科学内容容易造成科学知识的重复教授。同时，从文献资料来看，相较于设计数-科整合课程，学校层面协调好数学和科学教师的教学活动更有助于学生数学和科学的学习。①M. M. Hurley，“Reviewing Integrated Science and Mathematics：The Search for Evidence and Definitions from New Perspectives”，School Science and Mathematics，Vol.101，no.5（2001），pp.259-268.

（2）数-技整合是一种适宜的尝试

20 世纪90 年代，国际上兴起的MST（Mathematics，Science and Technology，即数学、科学与技术）整合课程运动，旨在帮助学生理解数学、科学和技术的关联性。其中，技术教育工作者既希望技术为学生学习和应用数学及科学概念提供跨学科情境，又希望通过MST 整合促使技术成为一个学校科目。②P. Forster，“Must we MST？”，Journal of Technology Education，Vol.6，no.1（1994），pp.76-84.在我国，数学教育界很早就认识到技术在数学教学中的重要性，《义务教育数学课程标准（2022 年版）》更进一步强调要促进信息技术与数学课程融合。因此，数-技整合是一种适宜的类型。事实上，由于数学是一种强有力的符号技术，数学课程本身就是一种特殊的数-技整合课程。

（3）数-工整合存在巨大的潜在价值

当前，工程及工程教育的重要性日益凸显，美国数学教育呈现出一种工程转型趋势。这启示着我国数学教育需融入工程要素，促进数学课程发展；进一步完善现有课程体系，创设工程教育平台；发展教师工程素养，打造强有力的数学教育师资。③马俊海，张维忠：《美国数学教育工程转型的缘起、进展与启示》，《浙江师范大学学报（自然科学版）》2023 年第2 期，第227-234 页。在此背景下，工程已成为新时代我国社会必不可少的一种文化系统，从丹尼斯·劳顿（Denis Lawton）的文化分析理论来看，在数学“综合与实践”课程中融入工程要素，能够在一定程度上实现我国现行义务教育课程体系的完整性。

三、设计可行性

1. 设计基于数学学科的STEM 课程存在理论可行性

从文献资料来看，新时代教师设计基于数学学科的STEM 课程有迹可循。我国数学教育工作者对数学“综合与实践”课程的理论研究和实践探索已有20 余年，为教师设计基于数学学科的STEM 课程积累了宝贵资料。其中，2000—2010 年为探索阶段，自《全日制义务教育数学课程标准（实验稿）》新增“实践与综合应用”领域以来，许多数学教育人员探讨了如何设计并实施小学和初中数学“综合与实践”课程④宋宝和，宋乃庆：《回归生活世界凸显自主选择——从两个教学实例谈小学数学实践与综合应用课程的自主选择》，《中国教育学刊》2004 年第7 期，第32-34 页。；2011—2016 年为发展阶段，数学教育人员聚焦实践中暴露出的问题，更加关注如何更好地落实数学“综合与实践”课程⑤张维忠，岳增成：《台湾数学“连结”评介》，《教育学术月刊》2014 年第10 期，第29-32 页，第94 页。；2017 年至今为深化阶段，《义务教育数学课程标准（2022 年版》）强化了数学课程的综合性和实践性，更多数学教育人员探讨了如何设计主题学习活动或开展项目式学习。⑥郭衎，曹一鸣：《综合与实践：从主题活动到项目学习》，《数学教育学报》2022 年第5 期，第9-13 页。

2. 设计基于数学学科的STEM 课程存在实践可行性

通过问卷调查，笔者发现许多中小学数学教师都知晓数学与科学、技术和工程存在内在关联，并有意愿设计基于数学学科的STEM 课程。然而，理论知识的欠缺、可参考案例的匮乏、学校支持的不足等因素，阻碍着教师在实践中设计基于数学学科的STEM 课程。从认知和情感层面来看，教师设计基于数学学科的STEM 课程存在实践可能性，这也启示着我国数学教育界应加快开展STEM 课程设计的理论研究与实践探索。如，高等师范院校应将如何设计STEM 课程纳入数学教师专业发展项目，中小学校应当为数学教师设计基于数学学科的STEM 课程提供必要支持。当然，要设计基于数学学科的STEM 课程，教师也应从多个维度加以回应，即树立多元文化数学观，形成超学科理念；发展跨学科教学兴趣，形成超学科态度；参与浸入式学习体验，增强跨学科意识；研习跨学科课程案例，落实跨学科教学。

四、设计策略

基于数学学科的STEM 课程为我国学生提供了一种解决问题的系统方法。设计基于数学学科的STEM 课程应以数学文化为基础，从文化视野重新审视STEM 学科关系。例如，乌比拉坦·达布罗西欧（Ubiratan D’Ambrosio）从民族数学项目（Ethnomathematics Program）出发来解读STEAM 关系，阐明了民族数学项目是开展STEAM 教育最重要的理论基础。①B.W. Zehlia，Promoting Language and STEAM as Human Rights in Education，Singapore：Springer Publisher，2019，pp. 163-175.基于此，本文提出了若干有助于教师设计基于数学学科的STEM 课程的策略。

1. 基于课程标准，以数学核心素养为始终，架构多维目标

基于数学学科的STEM 课程隶属于义务教育数学“综合与实践”学习领域，其设计必须以《义务教育数学课程标准（2022 年版）》为指导，并参照《义务教育课程方案（2022 年版）》《义务教育科学课程标准（2022 年版）》等课程文件。例如，数-工整合有巨大潜在价值，但我国数学课程标准并未涵盖中小学工程教育的内容和标准，那么教师在设计数-工整合课程时，就可参照科学课程标准中有关工程学习的要求，还可以《美国K-12 高质量工程教育框架》（The Framework for Quality K-12 Engineering Education）②T.J. Moore，A.W. Glancy，K.M. Tank，et al，“A Framework for Quality K-12 Engineering Education：Research and Development”，Journal of Pre-College Engineering Education Research，Vol.4，no.1（2014），pp.1-13.为指导，从而在数学“综合与实践”课程中融入工程要素，为我国中小学生提供一个深化学习工程的机会。同时，其设计要以数学核心素养为始和终，因为“素养”是一个多元、互联、动态和发展的概念，STEM素养是STEM 学科素养链的协同作用。③A. Zollman，“Learning for STEM Literacy：STEM Literacy for Learning”，School Science and Mathematics，Vol.112，no.1（2012），pp.12-19.换言之，通过帮助发展学生的数学核心素养，能够带动学生其他STEM 学科素养的发展。此外，架构多维目标可帮助学习者将STEM 学科与行动连接起来并超越它们。还需指出，教师对如何架构多维目标应有自主选择权。

2. 情境创设和内容选择应遵循文化回应理念，重视大概念

教师在创设问题情境和选择课程内容时应遵循数学文化回应理念，因为学习者及STEM 学科皆有文化多样性，这意味着教师要发展对“数学是一种文化现象”的广泛理解，认识到数学与科学、技术和工程的关联。同时，数学教师也应重视大概念（big ideas，又称“大观念”），它是将众多学科联系成连贯整体的关键性概念，是理解初等数学的基础。④R.I. Charles，“Big Ideas and Understandings as the Foundation for Elementary and Middle School Mathematics”，Journal of Mathematics Education Leadership，Vol.7，no.3（2005），pp.9-24.大概念能帮助学生突破数学学科壁垒，深化对STEM 本质和STEM 概念的理解。因此，大概念对于理解STEM 学科至关重要，综合起来代表了STEM 学科提供的世界模型。这要求教师要明确“STEM 大概念”（big ideas of STEM）和“关于STEM 的大概念”（big ideas about STEM）是两个不同概念。⑤C. Chalmers，M. Carter，T. Cooper，et al，“Implementing‘Big Ideas’to Advance the Teaching and Learning of Science，Technology，Engineering，and Mathematics（STEM）”，International Journal of Science and Mathematics Education，Vol.15，no.1（2017），pp.25-43.前者可分为内容大概念（如概念、原则、策略或模型）和过程大概念两个类别，后者侧重于STEM 的本质和话语，涉及STEM 实践共同体中参与者的思维习惯及他们如何创造、评价和发展知识。教师还要明确认识到STEM 大概念是个连续统一体，涵盖学科大概念、跨学科大概念和超学科大概念，从而选择和应用适切的STEM 大概念来设计基于数学学科的STEM 课程。

3. 采用单元教学，突出模型启发式活动等数学跨学科实践活动

单元是课程组织的基本单位，教师应着重从单元层面设计基于数学学科的STEM 课程，这是一个将“STEM课程单元”视为整体而进行的课程重组过程，需要教师考虑大概念的层级性、整合路径或方式的多样性及整合内容的适切性。同时，数学教师要突出模型启发式活动（Model-Eliciting Activities）、基于挑战的学习（Challenge-Based Learning）、工程设计过程（Engineering Design Process）等活动。例如，在设计数-工整合课程时，教师就可以设计基于挑战的工程设计任务，引导学生进行挑战性学习活动。换言之，教师设计数-工整合课程的一个策略是整合工程设计，让学生参与具体或抽象产品的设计。其中，知情设计是一种有效的STEM 教学策略。当然，教师要突出工程设计，有必要形成“告知教法观”。①范兆雄：《告知与设境催生：两种教法认识观的教学论图式》，《课程·教材·教法》2022 年第11 期，第106-112 页。此外，数学建模作为数学的核心，是通往STEM 教育的一座桥梁②M. Kertil，C. Gurel，“Mathematical Modeling：A Bridge to STEM Education”，International Journal of Education in Mathematics，Science and Technology，Vol.4，no.1（2016），pp. 44-55.，教师设计基于数学的STEM 课程应突出数学建模。

4. 理解数学素养导向评价理念，坚持“学-教-评”一致性原则

评价在教育活动中发挥着诊断、反馈、激励等作用，能够有效调控并促进教育改革。③靳昕，蔡敏：《美国中小学“21 世纪技能”计划及启示》，《外国教育研究》2011 年第2 期，第50-54 页，第77 页。在核心素养评价时代，评价是数学“综合与实践”课程改革取得成功的关键因素，这要求教师树立正确的评价观。在设计基于数学学科的STEM 课程时，教师要明确自己是一位评价者，要形成数学素养导向的评价理念。这要求教师在评价理念上着眼于学生的全面发展，能理解STEM 素养链的内在关联，明确素养导向评价与知识（或能力）导向评价之间的区别。通常，评价理念随着育人理念的变化而呈现出不同的发展样态。④张维忠，江漂：《素养导向的数学核心素养评价——〈义务教育数学课程标准（2022 年版）〉的新变化》，《中小学课堂教学研究》2022 年第7 期，第1-3 页，第7 页。在设计基于数学学科的STEM 课程时，教师也可能具有不同的课程评价观念，教师应从“针对基于数学学科的STEM 课程的评价”转变为“为了基于数学学科的STEM 课程的评价”，并逐渐形成“作为基于数学学科的STEM 课程一部分的评价”的观念。同时，教师应注重评价主体、评价内容及评价方式的多元化，采用动态互联的眼光来审视基于数学学科的STEM 课程设计，坚持“学-教-评”一致性原则。