倾斜式钢箱拱结构分析与设计
王 麒,于建立,郑亚林
(1.中建中原建筑设计院有限公司,郑州 450000;2.中国建筑第七工程局有限公司,郑州 450000)
随着环境保护和“双碳”战略的实施,以及全寿命周期设计理念的普及,钢结构得到越来越广泛的应用;随着社会和经济的发展,人们对建筑结构的景观性和美学要求越来越高。倾斜钢箱拱是一种受力良好的结构形式,又拥有非常好的景观效果,在工程中得到越来越多的应用,特别是一些景观效果显著的建筑。倾斜钢箱拱以受弯受压为主,又因为倾斜而存在很大的扭矩,复杂的受力使其稳定承载力难以确定。
倾斜钢箱拱介于拱和曲梁之间,相关理论自20 世纪50 年代以来得到广泛的研究。苏联学者Y. Schechtman[1]采用刚周边假定,认为曲梁中面没有剪切变形,创立了经典曲梁理论。Usami 等[2]假定非线性剪应变为零,考虑构件翘曲影响,列出了翘曲位移方程,被广泛用于拱问题分析。Kang 和Yoo[3]以Usami 的翘曲位移理论为基础,利用能量法避免了复杂的变形方程,推导了曲梁非线性问题的基本方程。我国学者李国豪[4]以梯形箱梁为对象研究了曲梁的弯曲扭转理论。程鹏[5]研究了两铰圆弧拱的非线性弯曲和弹塑性稳定。杨永华等[6-7]研究了开口薄壁截面圆弧拱的弹性稳定承载力,并推导了拱的弹塑性稳定的方程。康厚军[8]以倾斜拱桥为工程背景,研究了索拱结构的稳定。窦超等[9-10]分析了拱的平面外稳定性能,并研究了其设计方法。徐庆幸[11]以高强钢焊接工字形截面圆弧拱为对象,研究了其平面外的整体稳定性。许强、童根树[12-15]对薄壁曲梁弹性和弹塑性稳定极限承载力进行力研究,考虑翘曲位移,建立起一套适用任意开口薄壁截面圆弧曲梁线性和非线性理论,并提出了适用于实际工程的曲梁稳定公式。张哲等[16]提出了单轴对称工字形钢梁的弹塑性稳定系数。许强[17]总结了不同学者的研究方法和研究结果,并提出了适用范围更广的计算方法。
现有的研究多针对竖直拱或水平曲梁,对于倾斜拱的稳定问题缺乏研究。本论文结合工程实例,采用有限元软件,在考虑材料非线性和几何非线性的情况下对倾斜钢箱拱的失稳全过程进行数值模拟,分析其稳定承载力,为类似工程提供参考。
1 工程概况
某人行桥为下承式拱桥,主拱采用倾斜式钢箱拱,主梁采用平面弯曲的钢箱梁,拱和梁分别向2 个方向弯曲,遥相呼应,妙趣横生。桥长107 m,桥面净宽5 m,共设置13 根拉索,布置形式如图1 所示。

图1 人行钢拱桥布置图
钢箱拱整体对称布置,拱轴线采用二次抛物线,矢高35 m,矢跨比1∶3,两端拱脚通过拱座与承台连接,形成拱脚固结的无铰拱。钢箱拱在竖向倾斜15°,采用3 m×3 m 的钢箱截面,由于倾斜,钢箱拱在剖面图中呈菱形布置。钢箱拱采用Q345 钢,钢板厚均为22 mm,通长布置T 型纵向加劲肋,在拉索位置增设刚性横隔板,板厚30 mm,以承担和分散拉索的集中荷载。
有限元模型采用板单元建立,板单元能够考虑杆件约束扭转的翘曲和畸变,有很高的计算精度。有限元模型共建立6 607 个节点,6 708 个单元。钢箱拱两端固定于拱座上,模型对拱脚采用固结约束,完全约束节点的3 个平动和3 个转动自由度。结构采用Q345 钢材,为各向同性材料,密度76.98 kN/m3,弹性模量206 000 MPa,泊松比为0.3,剪切模量为79 230 MPa。材料塑性采用von Mises 屈服准则,屈服应力为345 MPa。
实际工程中人群荷载是通过主梁传递到拉索,再传递给钢箱拱,钢箱拱除了自重主要承受来自拉索的力,所以有限元模型在拉索对应位置施加集中力。成桥状态下的索力见表1。

表1 成桥状态下的拉索索力
对模型进行稳定性计算时,荷载将按照表中的索力成比例增加,每级加载的拉索力为表中荷载的0.4倍,共分15 步加载。由于不同拉索的索力不相等,为了表述方便,以中间拉索LS-7 的索力为代表索力。
2 倾斜钢箱拱位移变化
经数值模拟钢箱拱跨中位移变化如图2 所示。
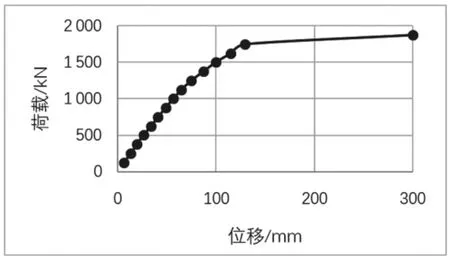
图2 钢箱拱荷载——位移曲线图
由图可知,刚开始跨中位移和荷载基本呈线性关系,当代表索力达到1 250 kN 后变形加快,此时材料还处于弹性阶段,变形加快主要是几何非线性的影响。索力达到1 747 kN 时,结构的最大位移不再是跨中位置的129 mm,而是1/4 跨的底板处的292 mm。根据应力计算结果显示,此时1/4 跨的底板处应力值为399 MPa,已达到屈服极限,发生了局部屈曲,而此时整个结构还可以继续承载,并未发生整体失稳。当荷载进一步增加时,跨中位移急剧增大,结构大部分进入塑性状态,钢箱拱失去承载能力。
由分析可以看出,在几何非线性和材料非线性的叠加影响下,倾斜钢箱拱从出现局部屈曲到整体失稳过程很短,表现出一定的突发性,这和钢箱拱的板件宽厚比、横隔板和加劲肋的设置有很大关系,工程中应注意稳定承载力的安全储备,并采用合理的构造以延缓局部屈曲到整体失稳的过程。
2.1 倾斜钢箱拱的变形
当代表索力为1 747 kN 时局部屈曲位置的位移已很大,代表索力为1 622 kN 时的变形更有参考价值,此时钢箱拱的变形即为失稳模态,如图3 所示。

图3 倾斜钢箱拱在极限稳定状态下的变形
钢箱拱每隔一段距离布置有横隔板,以限制钢板的局部失稳,在横隔板之间存在第二受力体系,钢箱拱的变形也表现出2 个体系的特征,分为整体变形和局部变形。整体变形以竖向变形为主,跨中向下变形,1/4 跨位置由于存在负弯矩而向上变形。局部变形以平面外变形为主,跨中的顶板和侧板发生了以横隔板间距为波节的变形,这是因为横隔板刚度较大;拱脚部位顶板和侧板都发生平面外变形,但它们的变形波节却又不完全相同;底板没有发生明显的平面外变形。最终变形是整体变形和局部变形之和,最大变形为114.6 mm,位于拱中间的上侧面。
当代表索力为1 747 kN 时钢箱拱出现局部屈曲,此时塑性发展情况如图4 所示,黑色为塑性发展区。可以看出1/4 跨位置率先进入塑性,说明此处的应力和内力较大。
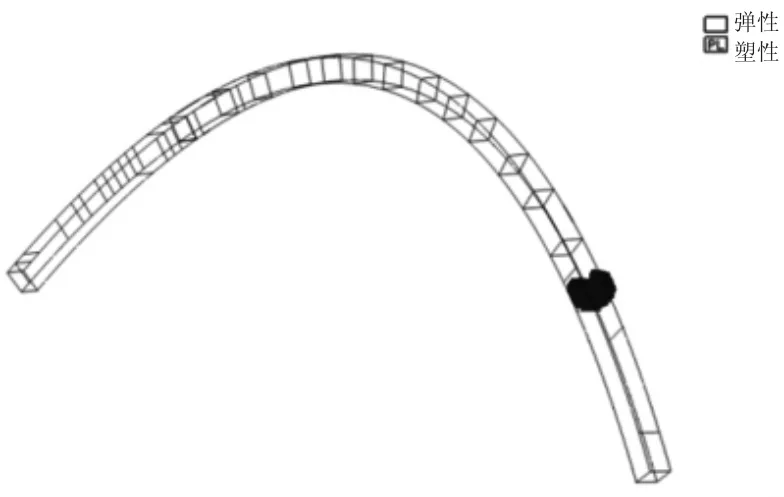
图4 结构塑性发展情况
2.2 1/4 跨内力图
根据计算,钢箱拱1/4 跨截面的弯矩和扭矩变化曲线如图5 所示。

图5 钢箱拱荷载——内力曲线图
图中Mx 为截面扭矩,Y 轴为截面竖直向下的坐标轴,Z 轴为截面水平坐标轴,My、Mz 分别为绕坐标轴的弯矩。由图可知,截面上以竖向弯矩Mz 为主,内力和荷载在前期呈线性增长,当代表索力达到1 747 kN 时竖向弯矩Mz 开始减小,但横向弯矩My 和扭矩Mx 开始加大,材料进入塑性状态,截面出现内力重分布。1/4跨截面变形较小,受几何非线性影响小,在材料非线性影响下内力出现了突然变化,这是造成钢箱拱突然失稳的主要因素。
2.3 钢箱拱应力分布
当代表索力达到1 747 kN 时钢箱拱已出现局部屈曲,应力进行了重分布,此时的应力分布不能代表正常使用时的应力分布。当代表索力为1 622 kN 时钢箱拱还处于弹性阶段,应力分布更具代表性,所以对此时的应力进行了分析。因为钢箱拱以受压为主,第二主应力比第一主应力更重要。钢箱拱的第二主应力云图如图6 所示。

图6 极限稳定状态空间曲梁的第二主应力图
von Mises 等效应力云图如图7 所示。

图7 极限稳定状态空间曲梁的von Mises 等效应力图
可以看出,最大应力出现在拱脚位置,拱脚也是弯矩最大的地方。需要注意的是最大应力出现的位置并不是严格的拱脚位置,而是距离拱脚一个波节左右的地方,这是因为叠加了第二受力体系下的局部应力。从von Mises 等效应力云图可以看出,还有很多位置应力值较小,材料强度没有得到充分利用,这可以通过优化构造设计来改善。
3 结论
本论文采用板单元对倾斜钢箱拱进行数值模拟,在考虑几何非线性和材料非线性的情况下分析了钢箱拱失稳的全过程,并分析了钢箱拱的内力变化和极限稳定状态下的变形和应力分布。主要结论如下:
1)倾斜钢箱拱从局部屈曲到整体失稳发展非常快,工程中应注意稳定承载力的安全储备。
2)倾斜钢箱拱在极限稳定状态下的变形包括整体变形和局部变形,整体变形在平面内为跨中向下、1/4跨向上的对称变形,局部变形为板材的平面外变形,最大变形出现在跨中侧板位置。
3)构造设计很重要,它直接影响第二体系下的局部变形和局部应力,工程中可通过合理的构造设计延缓倾斜钢箱拱从局部屈曲到整体失稳的发展历程,提高材料利用率。

