基于改进AHP-PSO的三模盾构掘进模式地质适应性研究

陈乔松, 郭俊平, 梁红兵, 马经哲, 陶江峰

(1.广州地铁集团有限公司, 广州 511430; 2.中铁隧道集团三处有限公司, 乐昌 512205;3.中铁(广州)投资发展有限公司, 广州 510000; 4.西南交通大学机械工程学院, 成都 610031)

在中国的城市轨道交通施工工程中,由于大多数城市地质水文条件较复杂,盾构施工时往往存在软土硬岩交替等恶劣施工条件,单模盾构机难以适应复杂多变的地质环境,地质适应性较好的复合盾构也就越来越多地应用于隧道工程。复合盾构即通过对刀盘刀具、土仓和出渣结构等的适应性设计使其具备两种或两种以上掘进模式从而能够在复杂地质条件下安全高效地掘进施工的盾构机,复合盾构的地质适应性分析及其掘进模式选取研究对于中国隧道工程领域的发展具有重要意义。

刘东[1]对双模式盾构的隧道掘进机(tunnel boring machine,TBM)和土压平衡(earth press balance,EPB)两种掘进模式的功能原理和适用范围进行了分析。赖理春[2]通过分析土压盾构和泥水盾构的施工特点提出了土压和泥水模式的适用工程条件。此类研究主要是通过分析不同掘进模式的功能原理、总结相关工程经验定性分析不同掘进模式的适用范围,并未涉及不同掘进模式地质适应性的深入分析。

吕睿虎[3]通过分析TBM设备指标和环境指标对TBM施工地质适应性进行了综合评价,其研究需要工程的掘进效率和工时利用率等信息,不适用于工程施工前的选型。颉芳弟等[4]运用测度理论构建了隧道掘进机地质适应性评价模型,其评价指标涉及TBM施工参数,也不太适用于工程施工前的选型。姚乐[5]通过分析影响EPB掘进的相关参数建立了土压平衡盾构掘进适应性评价模型,其研究对复合盾构土压平衡模式地质适应性量化分析有一定的参考作用。此类研究集中在土压平衡盾构和TBM的地质适应性分析,缺少对复合盾构的研究分析。

詹金武[6]基于模糊数学构建了TBM选型及适应性评价体系并通过案件推理(case-based reasoning,CBR)方法建立了TBM选型及适应性评价决策支持系统。赵斌[7]通过分析盾构的刀盘形式、道具结构、刀盘扭矩等关键结构及关键参数提出了一款隧道施工机械的选型配套分析方法,此类研究主要基于单模式掘进机,对于目前应用较多的多模盾构研究较少。

综上,对于复合盾构掘进模式地质适应性目前中外相关研究较少,同时,对于单模式掘进的地质适应性分析常采用传统层次分析法 (analytic hierarchy process,AHP)法,其权重计算可信度不高且容易稀释重要指标的权重。鉴于此,通过粒子群优化(particle swarm optimization,PSO)算法和改进AHP法进行三模盾构掘进模式地质适应性分析,以弥补对于复合盾构适应性设计的不足,为复合盾构掘进模式工程提供参考。。

1 三模盾构掘进模式地质适应性评价方法

1.1 改进层次分析法

层次分析法AHP是常用的模糊问题的量化求解方法[8-9],其主要求解步骤如下。

步骤1递阶建立层次结构。将模糊决策划分为目标层A、准则层B和指标层C,目标层为决策对象,准则层和指标层表征各级决策对象的影响因数。

步骤2构造判断矩阵。按照表1所示的九标度表两两对比以构建对应的判断矩阵F={fij}n×n。

表1 九标度表Table 1 Nine scale table

步骤3层次单排序及一致性检验。传统的层次分析法通过式1、2进行判断矩阵的一致性检验,其中RI的取值如表2所示。

(1)

表2 RI取值Table 2 RI value

(2)

式中:RI、CI、CR分别为随机一致性指标、一致性指标和一致性比值;n和λmax分别为判断矩阵阶数和最大特征值。

当CR<1时即认为其满足一致性检验,各层的单排序权重即为其判断矩阵最大特征值对应特征向量。

步骤4层次总排序及一致性检验。基于单排序权重计算指标层元素Ci对于目标层A的总排序权重,并根据式(3)进行总排序一致性检验。设B层中与Aj相关的因素的判断矩阵经一致性检验求得CI(j)、RI(j),w(j)为Aj的总排序权重,则B层次总排序一致性比例为

(3)

上述的一致性检验方法进行了近似处理,对于高阶判断矩阵的可信度较差,因此基于粒子群算法改进AHP的一致性检验及权重求解。根据AHP的基本理论和判断矩阵的构造原理,当判断矩阵及其权重满足式(4)时,即认为其完全满足一致性。

(4)

式(4)中:fik为判断矩阵F中第i行第k列元素;ωi、ωk分别为总排序权重中的第i与第k个元素,实际应用时判断矩阵难以完全满足一致性,因此可考虑将式(5)作为优化目标函数通过粒子群算法求解,从而得到一致性较好的权重向量。

(5)

步骤5计算指标隶属度。设定各评价指标的隶属度函数,根据所评价对象各指标实际值代入隶属度函数求得每个指标隶属度。

步骤6模糊问题量化求解。传统的AHP通过式(6)所示的并行逻辑结构进行模糊问题的量化评估,并行功能逻辑结构如图1所示,当指标数增加时其重要指标的权重会被稀释。

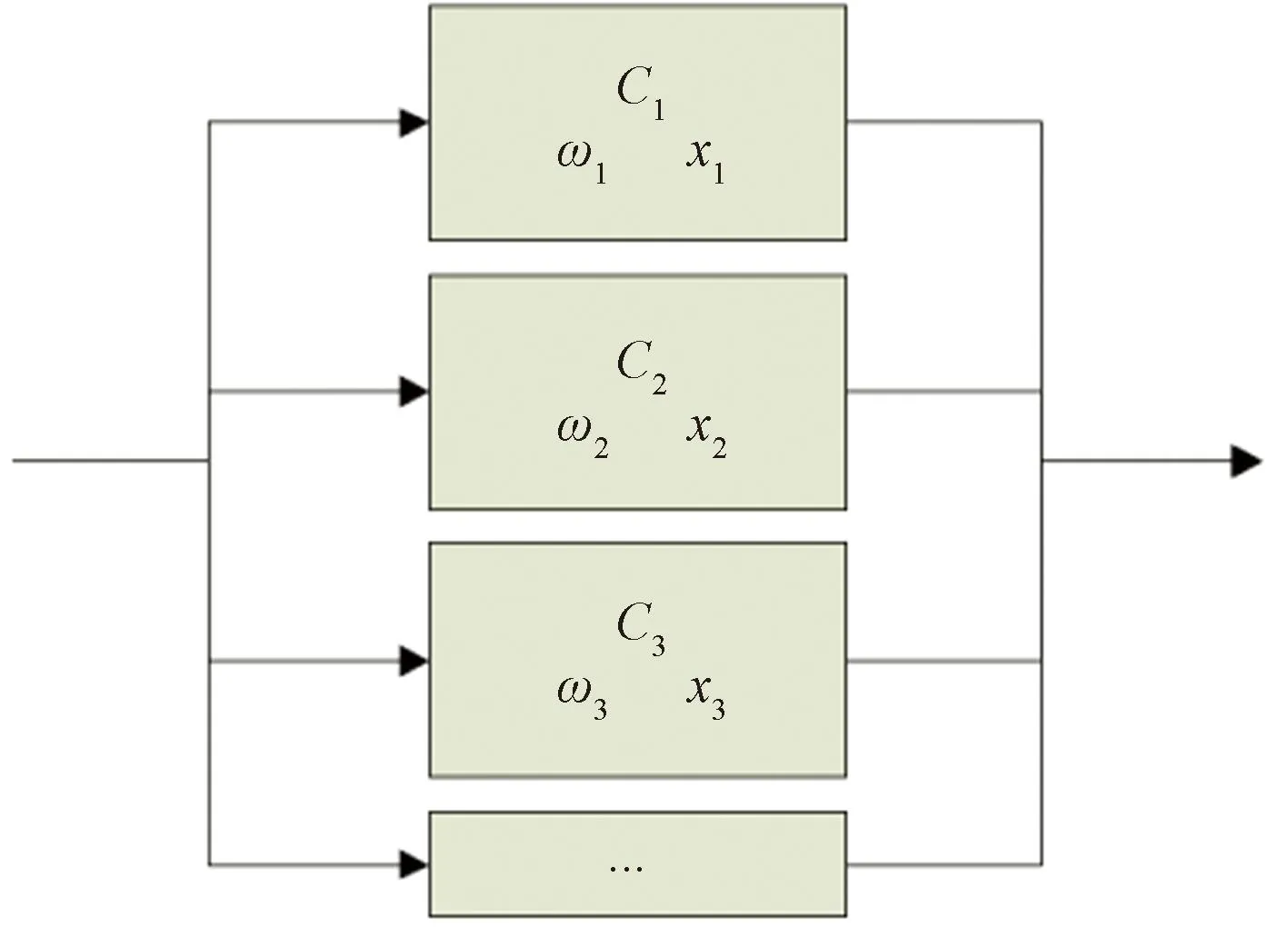
Ci为评价指标;xi为适应度;wi为权重图1 并行功能逻辑结构框图Fig.1 Parallel functional logic structure block diagram

其对应的量化评价值S可通过式(6)求解。

S=WX=ω1x1+ω2x2+…+ωnxn

(6)

为避免并行加权对涌水量等地质风险参数的权重稀释,可对重要指标建立图2所示的串联结构修正其对量化评价值的影响,其对应的量化评价可通过式(7)求解。

(7)

图2 串行功能逻辑结构框图Fig.2 Serial function logic structure block diagram

式(7)中:max(ω)为ωi中权重最大值。

采用图3所示的串并行混合功能逻辑结构可以避免重要指标的权重稀释[10-11]。

图3 混合功能逻辑结构框图Fig.3 Mixed function logic structure block diagram

设一模糊问题采用含有m个串行逻辑结构评价指标和n-m个并行逻辑结构评价指标组成的混合结构AHP进行定量分析,其量化评价值可通过式(8)求解。

(8)

1.2 粒子群算法

粒子群算法(particle swarm optimization,PSO)是受到飞鸟集群活动启发形成的一种优化算法,其利用群体中个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程,从而获得最优解[12-13]。其优化求解步骤如下。

步骤1确定粒子维度。PSO算法首先在求解空间中初始化一群粒子,每个粒子有位置、速度和适应度3个指标,其中位置通常表征优化问题的解的值,速度表征粒子在求解空间的变化速率,适应度表征粒子的好坏。

步骤2粒子群初始化。粒子群算法初始化需设定粒子数目、初始位置和初始速度。

步骤3最优位置求解。根据目标函数计算每轮的粒子适应度,依据其得到粒子个体最优位置pi(t)和全局群体最优粒子位置pg(t)。

步骤4迭代。根据式(9)所示的进化方程更新各粒子的位置和速度。

(9)

式(9)中:xi和vi为粒子的位置和速度;c1和c2分别为个体和群体学习速率;t为粒子迭代次数,根据文献[14],其取值均为0.2;r1和r2为[0,1]中的随机数,其用以避免粒子群算法陷入局部最优解。

步骤5求解最优解。

按照上述步骤反复迭代直到达到设定的迭代次数,或者优化问题达到需要的求解精度。

根据上述流程,以式(5)为目标函数进行评价指标权重求解,如图4所示。

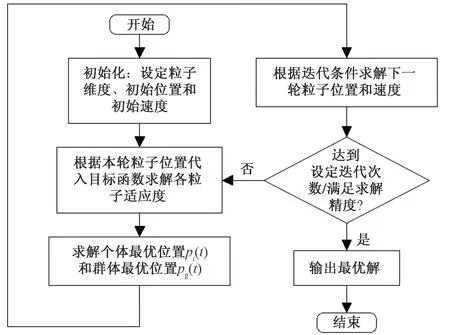
图4 权重求解流程Fig.4 Weight solving process

2 三模盾构地质适应性评价量化分析模型

根据前述的算法模型建立土压、泥水TBM 3种掘进模式的地质适应性量化分析模型。

2.1 地质适应性评价指标体系

三模盾构机某掘进模式在某特定地质环境中掘进施工时的掘进效率和施工质量即表征该掘进模式在对应地质下的地质适应性,其影响参数主要集中在基本地质条件、相关地质风险、盾构结构设计参数和工程需求指标等方面。

运用AHP的“分层递阶”思想分别建立土压、泥水、TBM 3种掘进模式的地质适应性评价指标体系如图5～图7所示。

图5 TBM掘进模式地质适应性评价指标体系Fig.5 Geological adaptability evaluation index system of TBM tunneling mode

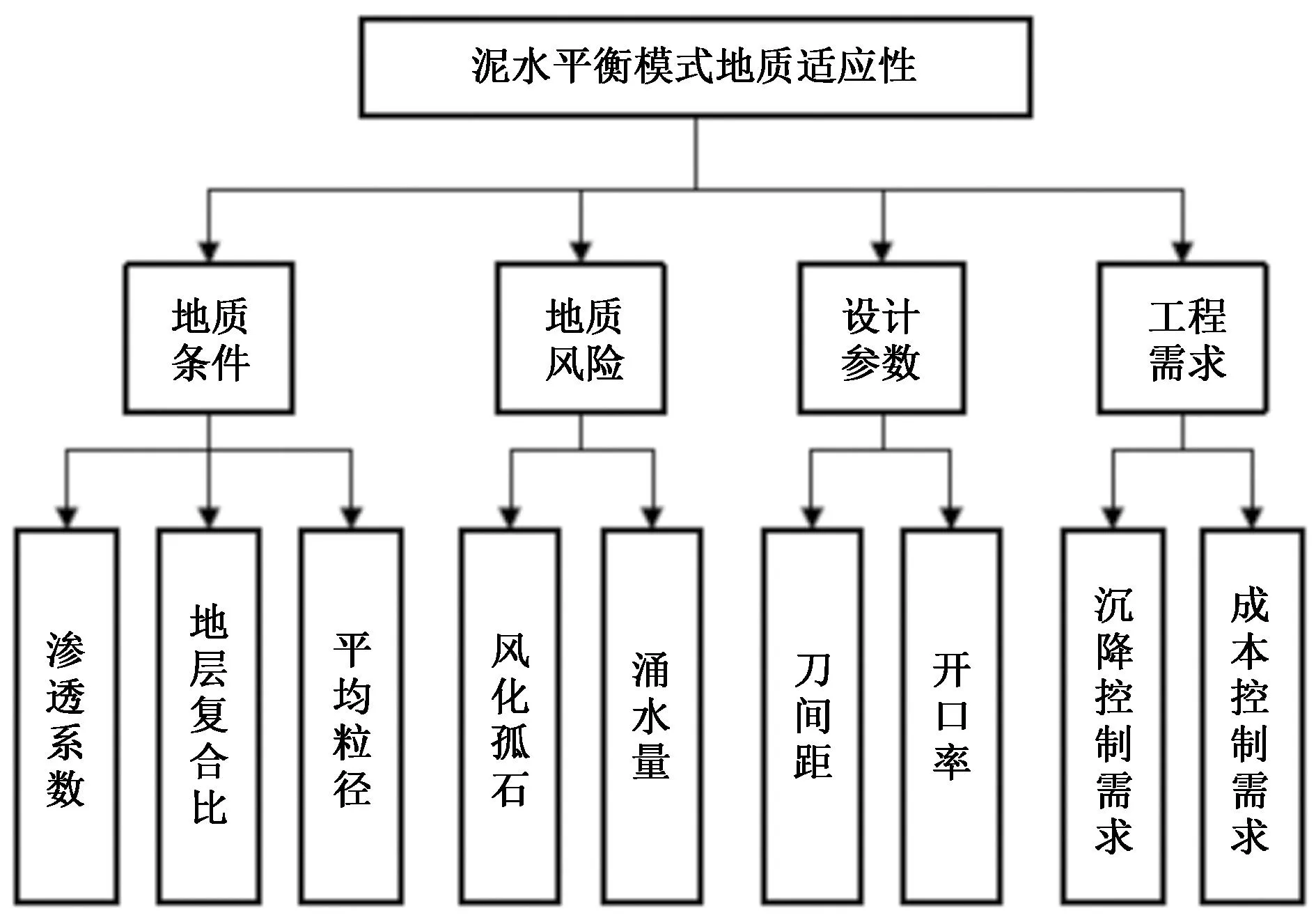
图6 泥水平衡模式地质适应性评价指标体系Fig.6 Geological adaptability evaluation index system of slurry balance model

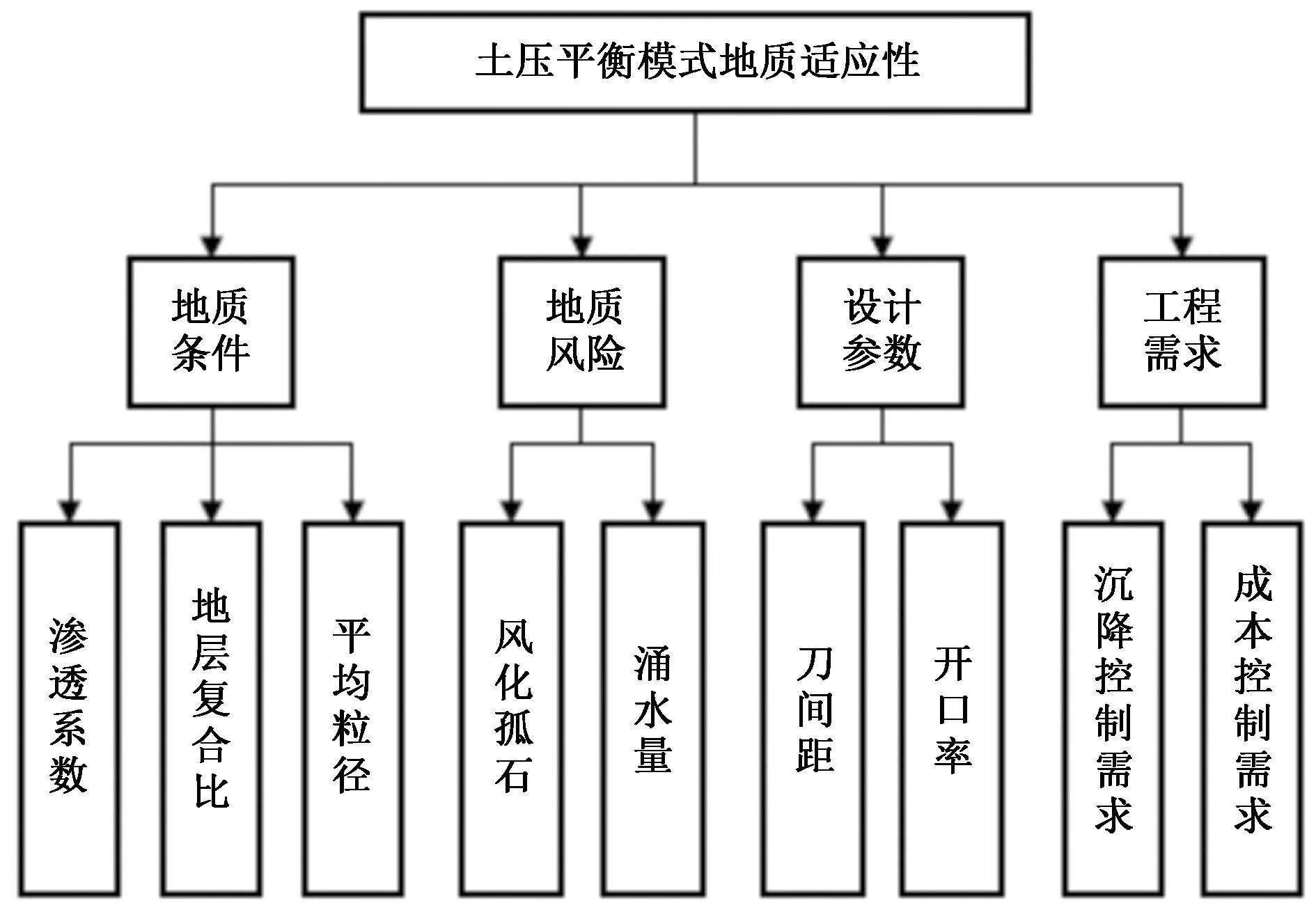
图7 土压平衡模式地质适应性评价指标体系Fig.7 Geological adaptability evaluation index system of earth pressure balance model

2.2 构建判断矩阵

依据九标度表,通过四位隧道工程领域的资深专家开会讨论,分别构建3种掘进模式的判断矩阵,具体如下。

(1)土压。

(10)

(2)泥水。

(11)

(3)TBM。

(12)

式中:E1、S1和T1分别为土压、泥水和TBM的准则层(地质条件、地质风险、设计参数、工程需求)对目标层的判断矩阵;E2～E5、S2～S5、T2～T5为相对应的指标层对准则层的判断矩阵。

2.3 基于粒子群算法求解权重及一致性检验

参考图4所示的权重求解流程,在MATLAB中构建粒子群算法模型求解评价指标权重,以土压平衡模式的A1-B层为例,将各层判断矩阵作为参数输入到算法中,以式(5)为目标函数,式(8)为迭代方法,得到最优粒子适应度随迭代次数的变化如图8所示。

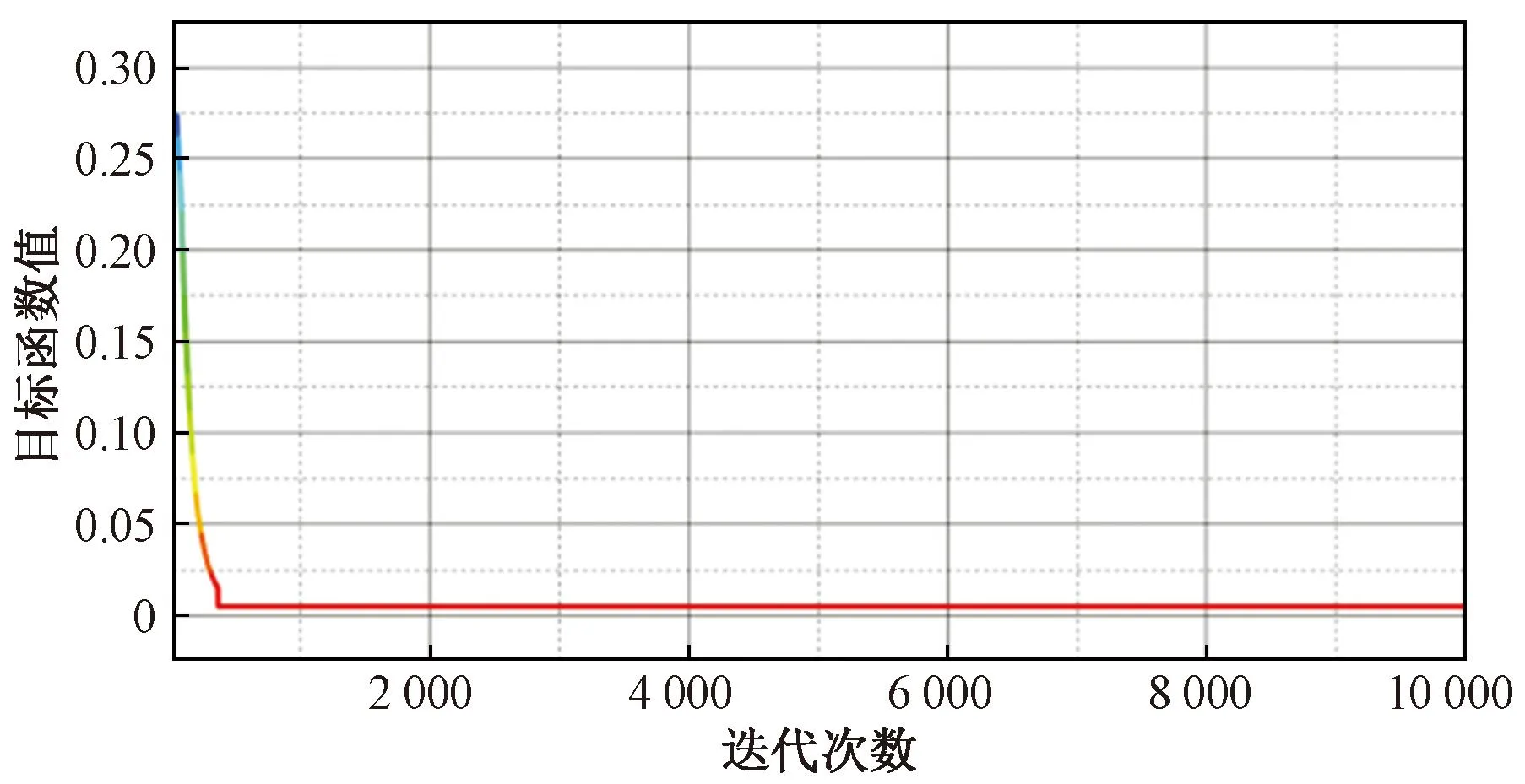
图8 求解精度随迭代次数变化曲线Fig.8 Curve of solution accuracy with the number of iterations

从图8可以看出,经过上百次迭代后目标函数值基本稳定在0.01一下,取迭代10 000次以后的最优粒子坐标作为优化得到的权重值,{B1,B2,B3,B4}的权重值为{0.266 0,0.453 8,0.139 6,0.140 6}。

同理可得土压、泥水、TBM 3种掘进模式地质适应性各评价指标权重如图9所示。

2.4 建立评价指标隶属度函数

由于各个评价指标的量纲和对不同掘进模式的掘进施工效率和质量的影响程度不尽相同,模糊数学中用区间[0,1]上的数值来表示元素与模糊集合的关系。

表3为各个评价指标的评价标准。考虑到渗透系数、涌水量等指标存在跨数量级的数值变化,以线性关系和对数关系建立各个指标的隶属度函数,当指标数值位于区间Ⅰ时,其隶属度为1,位于区间Ⅱ时其隶属度以线性或对数关系在[0,1]上变化,其余为0,所建立的主要隶属度函数如表4～表6所示。

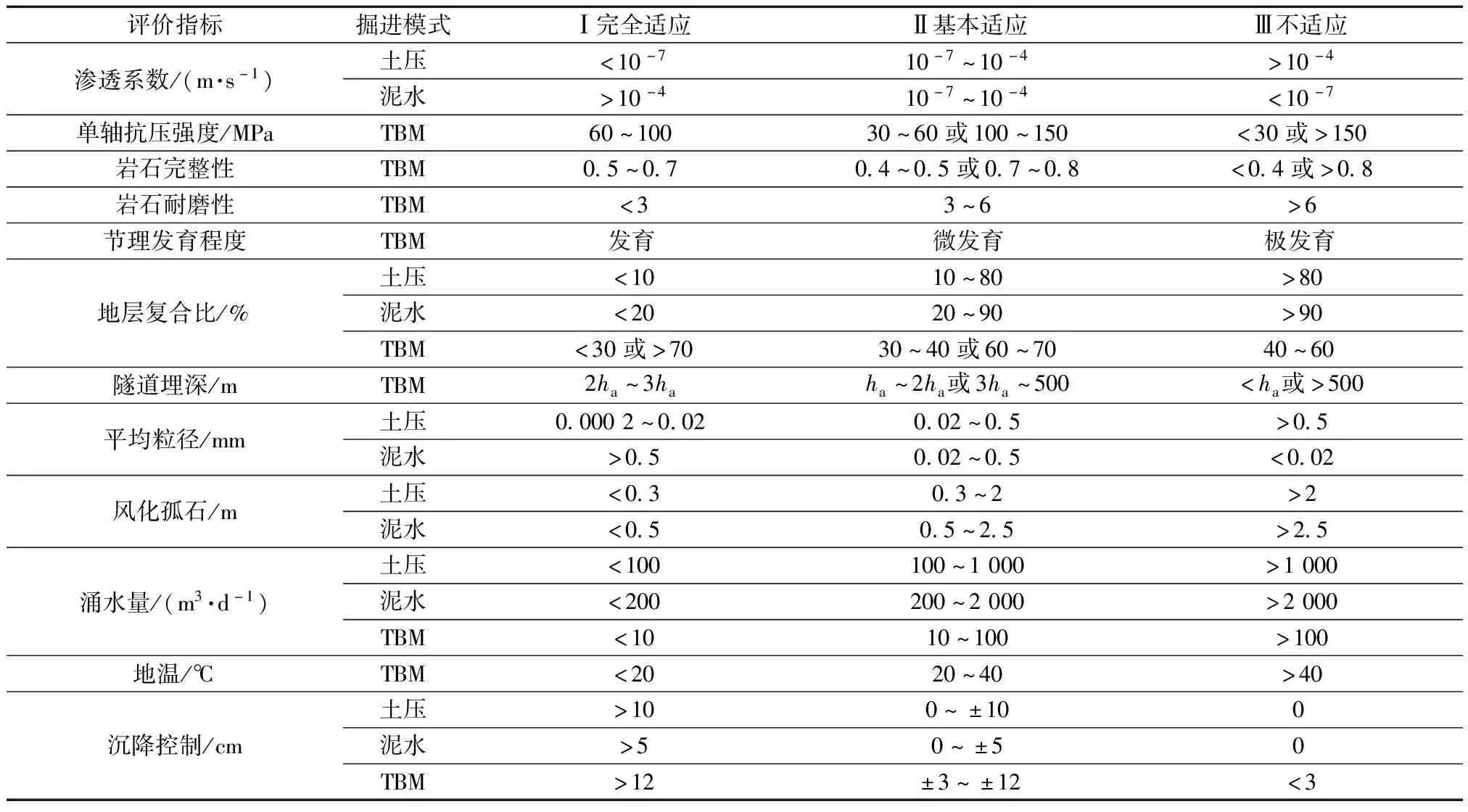
表3 各地质适应性评价指标评价标准Table 3 Evaluation criteria of various geological adaptability evaluation indexes

表4 土压平衡模式地质适应性评价主要隶属度函数Table 4 Main membership function of geological adaptability evaluation of earth pressure balance model

表5 泥水平衡模式地质适应性评价主要隶属度函数Table 5 Main membership function of mud-water balance model geological adaptability evaluation

表6 TBM掘进模式地质适应性评价主要隶属度函数Table 6 Main membership function of geological adaptability evaluation of TBM tunneling mode

2.5 基于改进AHP法求解掘进模式地质适应性

在实际盾构施工选型时中,通常需要优先保障涌水量等地质风险参数得到满足,随后要考虑地层沉降、经济性等的影响,最后才是根据其他参数进行选型。因此,基于混合功能逻辑结构改进的AHP进行掘进模式地质适应性分析。图10～图12为土压、泥水和TBM对应的混合功能结构。结合图10～图12所示的混合功能结构,根据式(7)即可求得各掘进模式的地质适应性量化值。

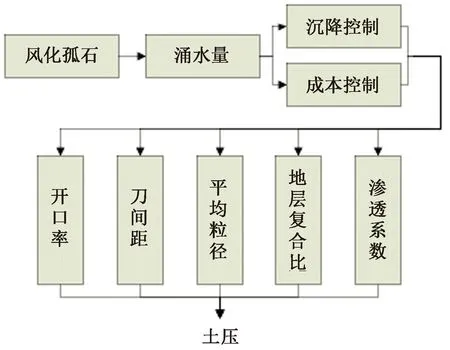
图10 土压掘进模式对应混合功能结构Fig.10 The earth pressure excavation mode corresponds to the mixed functional structure

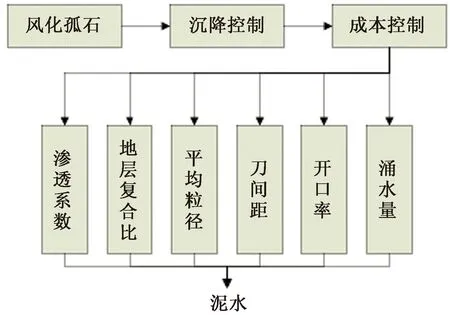
图11 泥水掘进模式对应混合功能结构Fig.11 Slurry tunneling mode corresponds to mixed functional structure

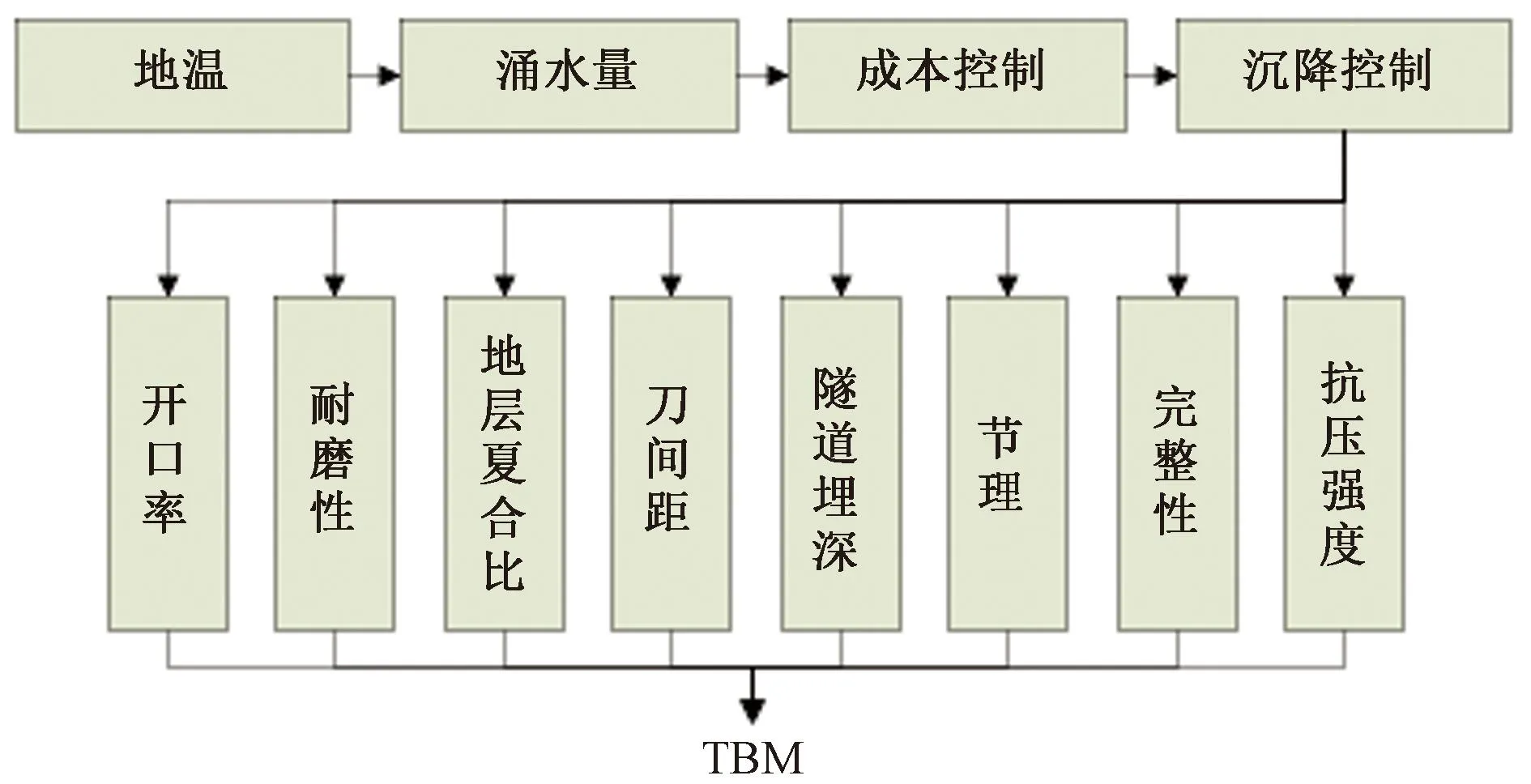
图12 TBM掘进模式对应混合功能结构Fig.12 TBM tunneling mode corresponds to the mixed function structure

3 工程实例验证

3.1 工程概况

广州地铁7号线二期工程萝岗站～水西站区间隧道左线起讫里程ZDK40+713～ZDK41+799,长1 086 m,采用集成有土压、泥水、TBM 3种掘进模式的三模式盾构掘进施工。其沿线穿越地层主要为不同风化程度的花岗岩,沿线均为孤石发育区,左线ZDK40+713～ZDK40+945段钻孔孤石发育率为66.7%,为孤石强烈发育区,左线地质纵断面如图13所示。

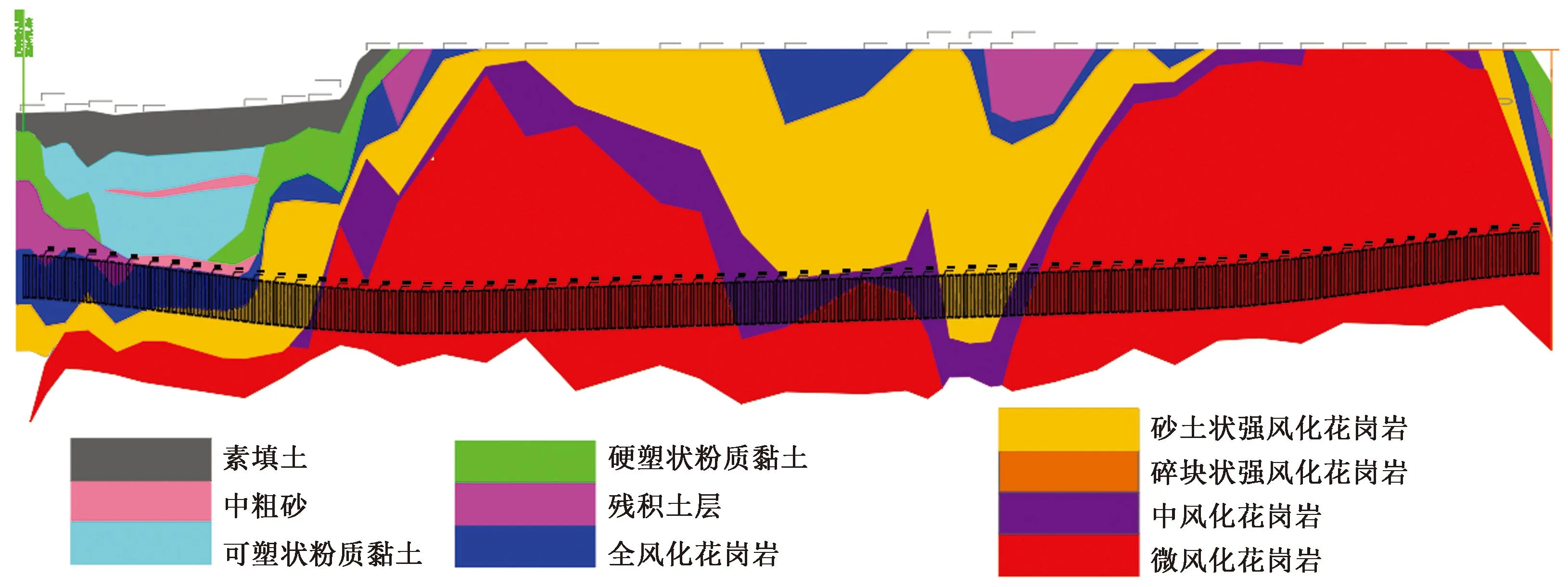
图13 广州地铁7号线萝岗-水西区间地质纵断面图Fig.13 Geological profile of Luogang-Shuixi section of Guangzhou Metro Line 7

上述区间穿越地层复杂多变,现有单模或双模盾构难以胜任,施工中采用了具有土压、泥水、TBM 3种掘进模式的盾构机,如图14所示,其能够实现在3种掘进模式之间一键切换[15]。盾构开挖直径Φ6 280 mm,刀盘配置复合式刀盘,其开口率达30%;配置59.94 cm中心双联滚刀、38把59.94 cm单刃滚刀以及47把刮刀、12组边刮刀。该三模式盾构的TBM掘进模式通过泥水排渣管道排出渣土,省去了中心皮带机,优化了其内部空间配置。

图14 三模式盾构机Fig.14 Three mode shield machine

3.2 掘进模式地质适应性分析

三模式盾构掘进区间左线长1 086 m,其穿越软土、硬岩及软硬不均等复杂地质,在进行掘进模式选取推荐时将其划分为前110、110～135、135～142、143～434、435～479、480～724环区段,每个区段地质参数相近,便于选取合适的掘进模式指导工程施工。

以左线435～479环为例,根据萝岗～水西三模式盾构施工区间的地质勘测资料,其地质参数及对应隶属度如表7所示。

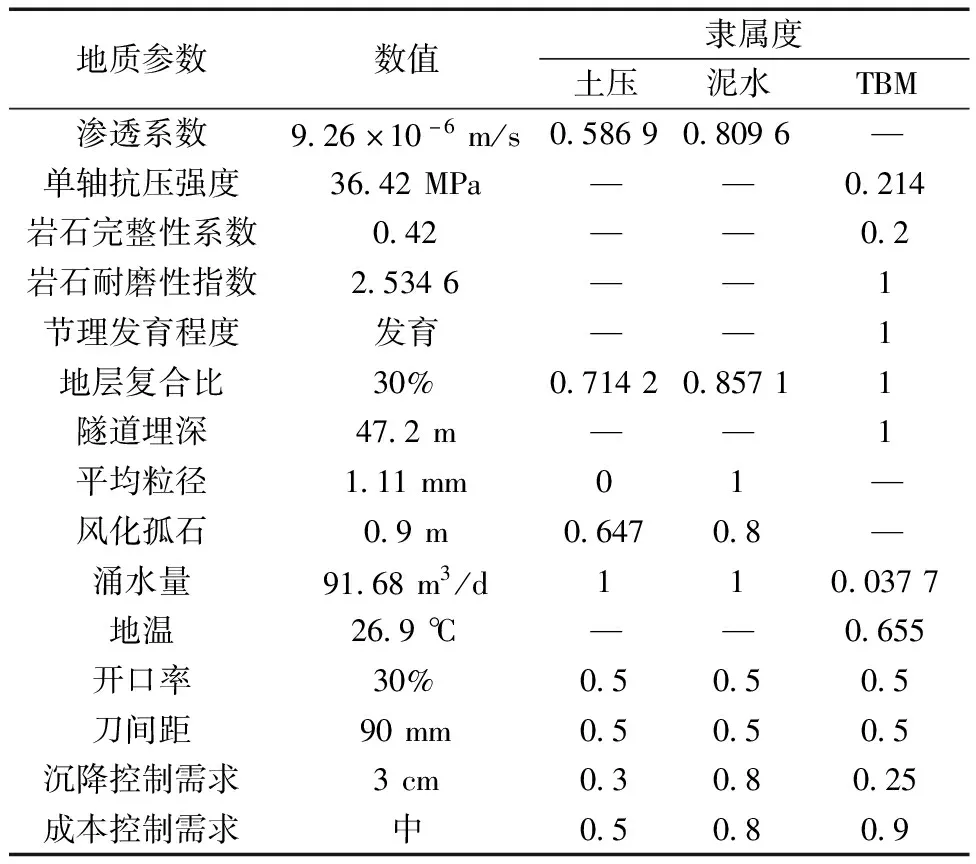
表7 435环～479环地质参数及隶属度Table 7 Geological parameters and membership degree of rings 435 ～ 479

结合表3的权重代入式(7)中计算可得土压平衡模式、泥水平衡模式和TBM掘进模式的适应性量化指标为{0.635 6,0.781 9,0.161 9}。当量化值大于0.5时,即认为其在对应地质条件下适应性很好。可以看出,萝岗—水西区间435～479环泥水平衡模式适应性优于土压优于TBM,基于最大适应度原则该段建议选取泥水平衡模式施工。同理可分析得到左线其余区段掘进模式选取方案如表8所示。

表8 萝岗-水西区间三模式盾构掘进模式选取推荐Table 8 Luogang-Shuixi three shield tunneling modes are recommended

广州地铁7号线二期工程三模式盾构掘进区间左线基本掘进完成,依托本文模型得到的掘进模式选取方案在实际工程中掘进效果良好。所建立三模盾构掘进模式地质适应性分析模型具备一定的工程指导意义。

4 结论

(1)以渗透系数、岩石单轴抗压强度、沉降控制需求等为评价指标,基于改进AHP-PSO算法建立了三模式盾构掘进模式地质适应性计算分析模型,定量分析一定地质条件下的各掘进模式地质适应性。

(2)基于PSO算法进行指标权重计算和一致性检验避免了传统AHP的不足,采用改进AHP法避免了重要指标被稀释权重。

(3)广州地铁7号线二期工程三模式盾构施工工程是中国三模盾构的首次尝试,基于其进行了三模盾构掘进模式地质适应性分析,对于多模式盾构的发展应用具有指导借鉴作用。