基于动态加权差分主成分分析的故障检测

张谦谦, 王文标, 郝友维

(大连海事大学船舶电气工程学院, 大连 116026)

随着生产需求的快速增长,现代化工业蓬勃发展,生产过程越来越集成化和复杂化。而复杂系统各环节紧密相连,即使发生微小的故障都可能会造成巨大的财产损失和人员伤亡,因此故障检测技术在现代工业生产中具有重要意义[1-4]。以主成分分析[5-9](principal component analysis, PCA)为代表的数据驱动方法,已经广泛应用于工业系统的过程监控和故障检[10-15]。然而使用PCA方法进行故障检测的前提是数据为单模态且样本之间相互独立,对于具有多模态特性和动态特性系统故障检测效果不佳。

多模态数据通常具有中心漂移、方差差异明显等特征。对于这一问题,可建立多个局部模型或全局模型来解决。李元等[16]采用基于K均值聚类方法对数据进行分类,为各个模态单独建立模型。由于故障检测效果与模型划分结果紧密相关,因此该方法对模型划分精度要求较高。张成等[17]提出了基于k近邻主元得分差分的故障检测方法,采用得分差分方法降低了数据多模态特性对故障检测的不利影响,但其未考虑不同特征对评价指标的贡献差异。冯立伟等[18]提出了基于权重k近邻的故障检测方法(fault detection of weightedknearest neighbor,FD-wkNN),通过寻找样本的k近邻并利用其加权近邻距离信息,解决样本中心漂移问题。但当样本不均匀时,对稀有样本的故障检测精度会降低。顾幸生等[19]采用局部近邻标准化(local neighborhood standardization, LNS)方法对数据进行标准化处理,消除了数据的多模态特性。但当故障数据的邻域信息来自多个模态时,经该方法处理后会造成故障数据与正常数据混叠,降低了故障检测精度。

对于动态系统,各参数的变化需要经过一定的滞后时间才会影响到其他变量的变化,且运行数据是根据时间采样的时间序列数据,因此在进行故障检测时要考虑数据的时序特性。对此,来颜博等[20]使用动态主元分析法(dynamic principal component analysis, DPCA),通过增加延时测量值构成增广矩阵提取系统动态特性,但其无法描述样本的自相关性且增大了数据维度,降低了计算效率。李元等[21]提出了时空近邻标准化(time-space nearest neighborhood standardization, TSNS)方法,通过寻找样本的时间和空间的局部近邻并进行标准化处理,消除了数据的动态特性。

针对系统的多模态和动态问题,提出动态加权差分主成分分析法 (dynamic weighted differential principal component analysis, DWDPCA)。设置合理长度的时间窗描述系统的动态特性,并寻找时间窗中样本在空间上的第一近邻和第一近邻的近邻集,利用加权差分方法解决数据中心漂移的问题,使用PCA进行异常检测。该方法兼顾了样本的时序特性和空间特性,适用于具有动态特性和多模态特性的系统,可提高系统的故障检测率。

1 基于动态加权差分主成分分析法的故障检测

1.1 主成分分析法

选取系统在正常工况下运行产生的历史数据,构建样本矩阵X=(Xij)n×m,其中,m为样本的变量数量,n为样本数量。使用z-score法将数据标准化,并计算其协方差矩阵S,计算公式为

(1)

主元个数由累计方差贡献率(cumulative percent variance, CPV)确定,其表达式为

(2)

式(2)中:λj为S的特征值。

(3)

Ti=XiPi

(4)

式中:XP为主元子空间中样本向量X的投影;Ti为得分矩阵;Pi为负荷矩阵;E为残差子空间。

T2和SPE统计量是PCA进行故障诊断的两个重要指标。T2统计量的控制限CLT2可表示为

(5)

式(5)中:α为显著性水平;1-α为置信度;Fα(α,n-α)为F分布,其第一自由度为α,第二自由度为n-α。

SPE统计量的控制限CLSPE可表示为

(6)

(7)

(8)

式中:cα为标准正态分在布置信水平为α时的置信限;h0为阈值;θ1和θ3为数据集的一分位数和三分位数;θi的定义如式(7)所示;λ为特征值。

1.2 动态加权差分主成分分析法

传统的PCA方法适用于数据服从独立同分布的单模态系统,对具有时序特性或多模态特性的系统检测效果并不理想。为提高PCA对具有的动态特性和多模态特性系统的故障检测性能,提出动态加权差分主成分分析法。通过时间窗描述样本间的时序关系,利用加权差分法解决数据中心漂移问题,使用PCA方法进行故障检测。具体方法如下。

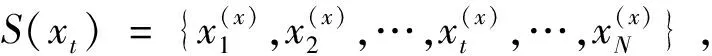
(9)

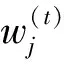
(10)

权值公式的约束条件如式(11)所示。

(11)

1.3 DWDPCA的故障检测

DWDPCA法故障检测流程图,如图1所示。

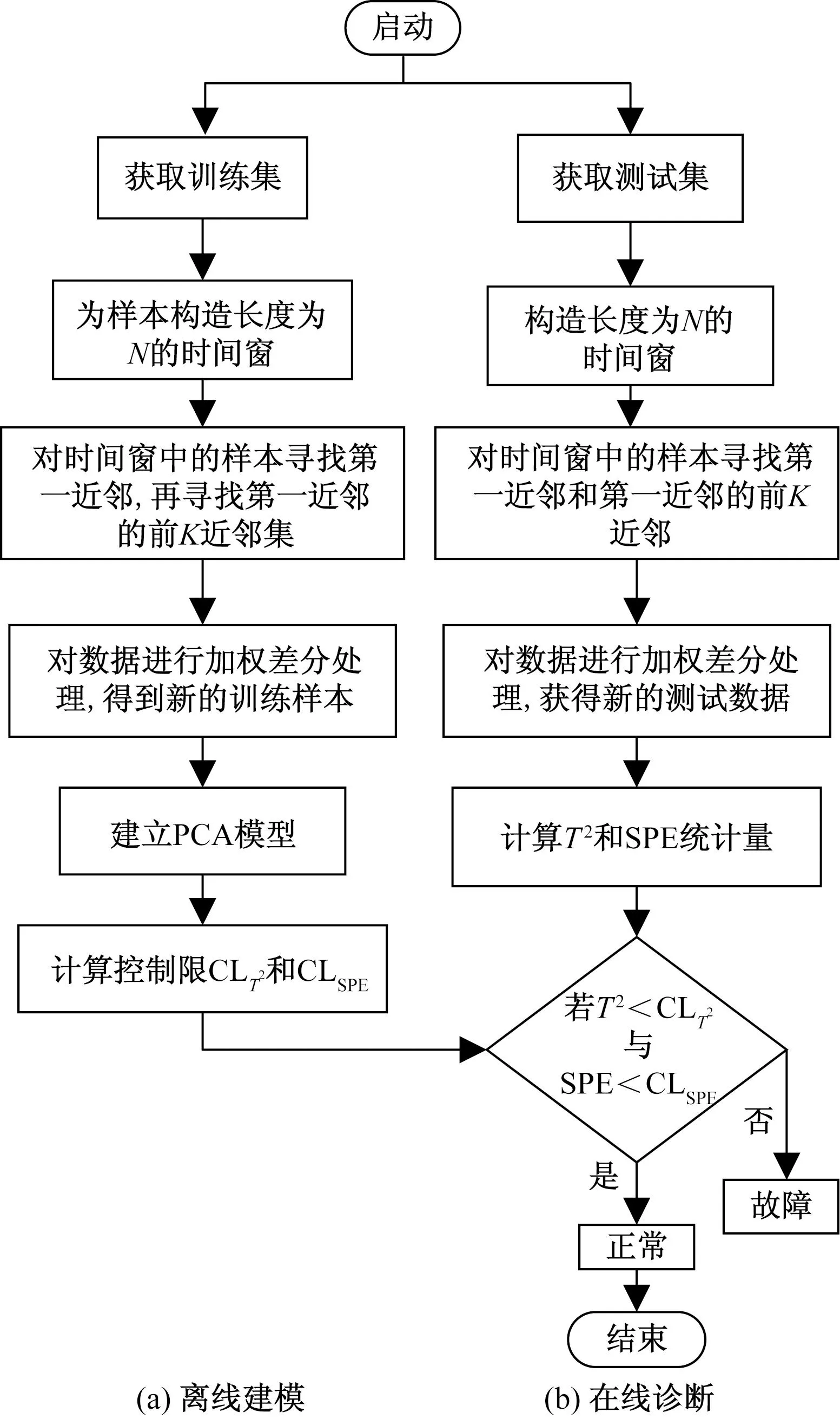
图1 故障诊断流程图Fig.1 Flowchart of fault diagnosis

利用动态加权差分主成分分析法进行故障检测主要分为:离线建模和在线诊断,具体步骤如下。

1.3.1 离线建模

步骤1获取正常工况下的历史数据作为训练集X。

步骤2对训练集中的每个样本xt设置合理的时间窗,再对时间窗中的样本寻找其空间上的第一近邻和第一近邻的K近邻集。

步骤4构建PCA模型,计算控制限CLT2和CLSPE。

1.3.2 在线诊断

步骤1获取要检测的样本作为测试集X*。

步骤2对测试集样本x*构造时间窗,并对时间窗中的样本在训练集中寻找第一近邻和第一近邻的K近邻集。

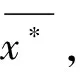
步骤5判断T2和 SPE统计量与控制限CLT2和 CLSPE的关系,若超限则说明此时系统发生故障,否则认为系统运行正常。

2 仿真结果与分析

分别利用数值仿真系统和Tennessee Eastman(TE)仿真平台模拟工业系统运行过程,并对其进行故障检测来验证该方法的有效性。

2.1 数值仿真

使用具有时序特性的数值仿真系统模拟多模态数据,仿真过程为

(12)

式(12)中:x1和x2为输出变量;t为时间变量;θ为角度;e1、e2为服从[0 ,0.01]的随机噪声;a、b为过程参数,通过改变其值来产生多模态数据,模态一中设置a为0.2;b为0.2,模态二中设置a为0.1,b为-2。

系统在模态一下运行4π时间后切换到模态二继续运行4π时间,每个模态生成500组数据,构成1 000组训练数据。再次让系统重新运行,每个模态各生成250组校验数据和250组故障数据,其中故障数据为在变量t上添加幅值为-6的阶跃信号所造成。系统产生的多模态数据散点图如图2所示。可以看出,正常数据的中心随时间逐渐变化,故障样本偏离正常轨迹,靠近前半段正常数据。

x1、x2为仿真模拟系统模拟出的数据图2 数值例子散点图Fig.2 Scatter plot of numerical examples

图3和图4分别为原始数据和经LNS方法处理后的测试集数据散点图和分布图。由图4可知, LNS方法均可将数据化为单模态且近似服从单峰高斯分布,符合使用PCA方法进行故障检测的前提条件,降低了多模态结构对故障检测性能的影响。但LNS方法并未考虑数据的时序特性,对具有动态特性的系统进行故障检测时存在不足。使用可以解决时序问题的动态加权差分(dynamic weighted differential, DWD)方法对数据进行处理,处理后的数据散点图及校验数据直方图如图5所示。

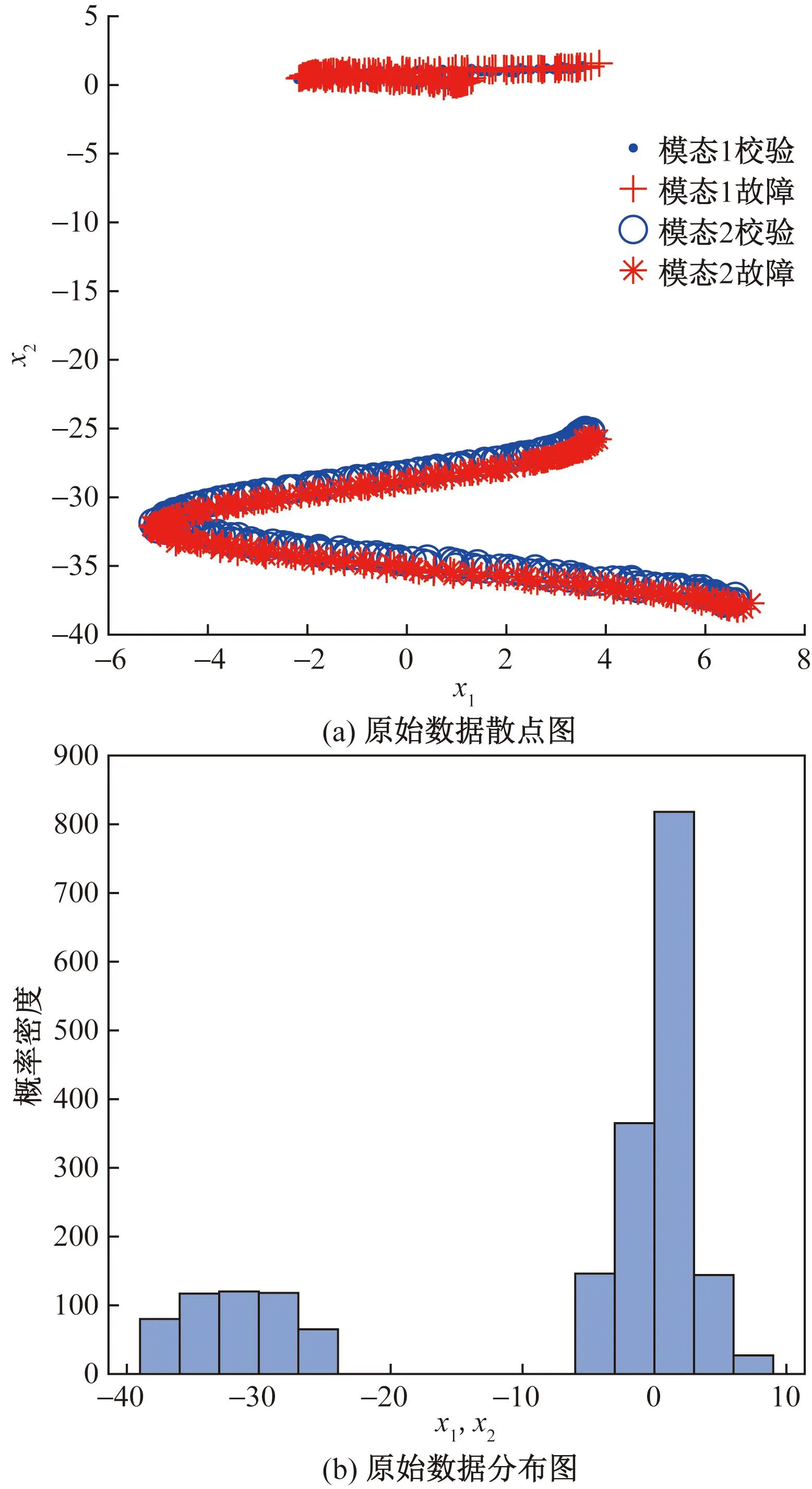
图3 原始数据散点及分布图Fig.3 Original data scatter and distribution map

图4 LNS处理后数据散点及分布图Fig.4 Data scatter and distribution after LNS processing

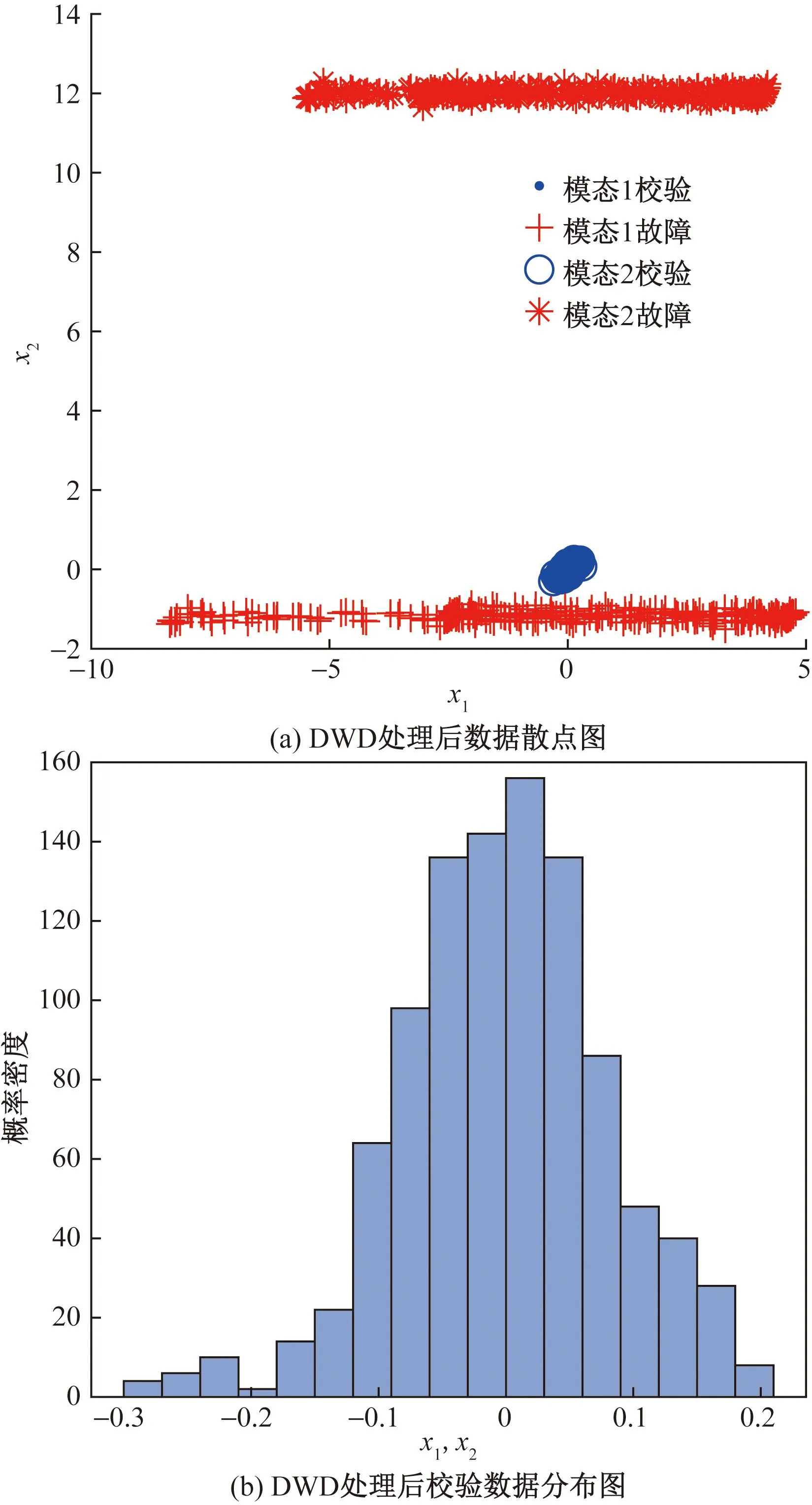
图5 DWD处理后数据散点及分布图Fig.5 Data scatter and distribution after DWD processing

同一数据分布区域内,故障数据与正常数据在空间上分布相近,但在时序上其分布却存在明显差距。因此设置时间窗可有效描述样本间的时序关系,实现正常样本与故障样本的有序排列,避免了只寻找样本的空间近邻,而忽略了样本间的时序特性。解决了样本时序特性对故障检测的影响后,再寻找样本的第一近邻和第一近邻的近邻集对数据进行加权差分处理,消除了数据的多模态特性。经DWD方法处理后,故障样本远离坐标原点,可将故障样本从正常样本中分离出来。

经DWD方法处理后的数据具有正态特性,即样本间是相互独立的,消除了数据的时序特性。因此要选取合适的时间窗长度L,若数据选择过大,则会增加计算复杂度。若选择过小,则无法对当前时间段系统的动态特性进行准确描述。本实验使用交叉验证的方法选取最佳L和K,设置时间窗长度L为5,近邻数K为5。使用DWD方法进行数据处理,由图5可以看出,该方法可有效处理具有动态特性的多模态数据,将其转化为单模态数据且服从高斯分布,并将故障样本与正常样本分离。使用PCA和DWDPCA方法对测试集数据进行检测,设置置信度为99%,累计贡献率为85%,检测结果如图6和图7所示。

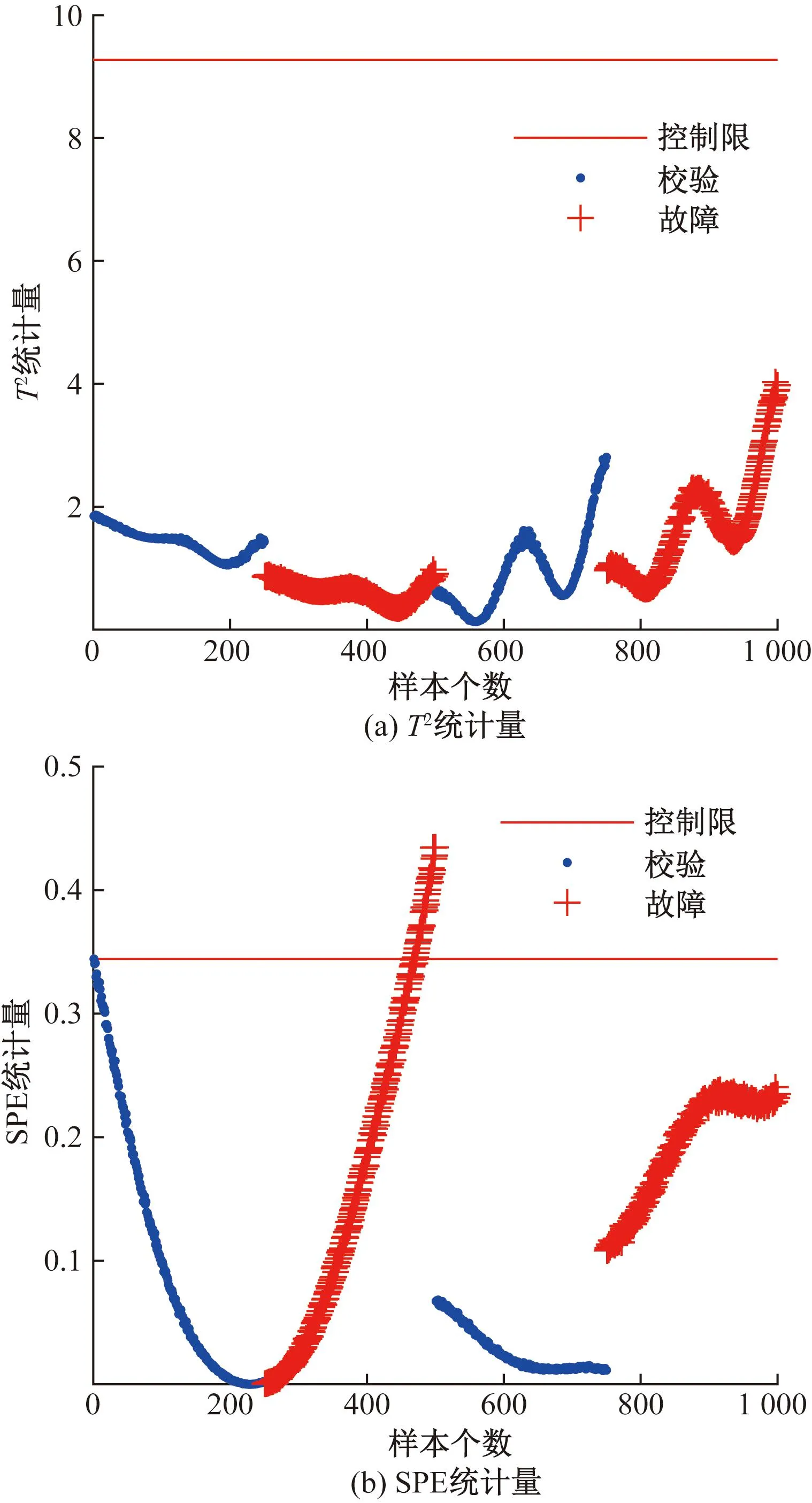
图6 数值例子PCA故障检测图Fig.6 PCA fault detection diagram for numerical examples

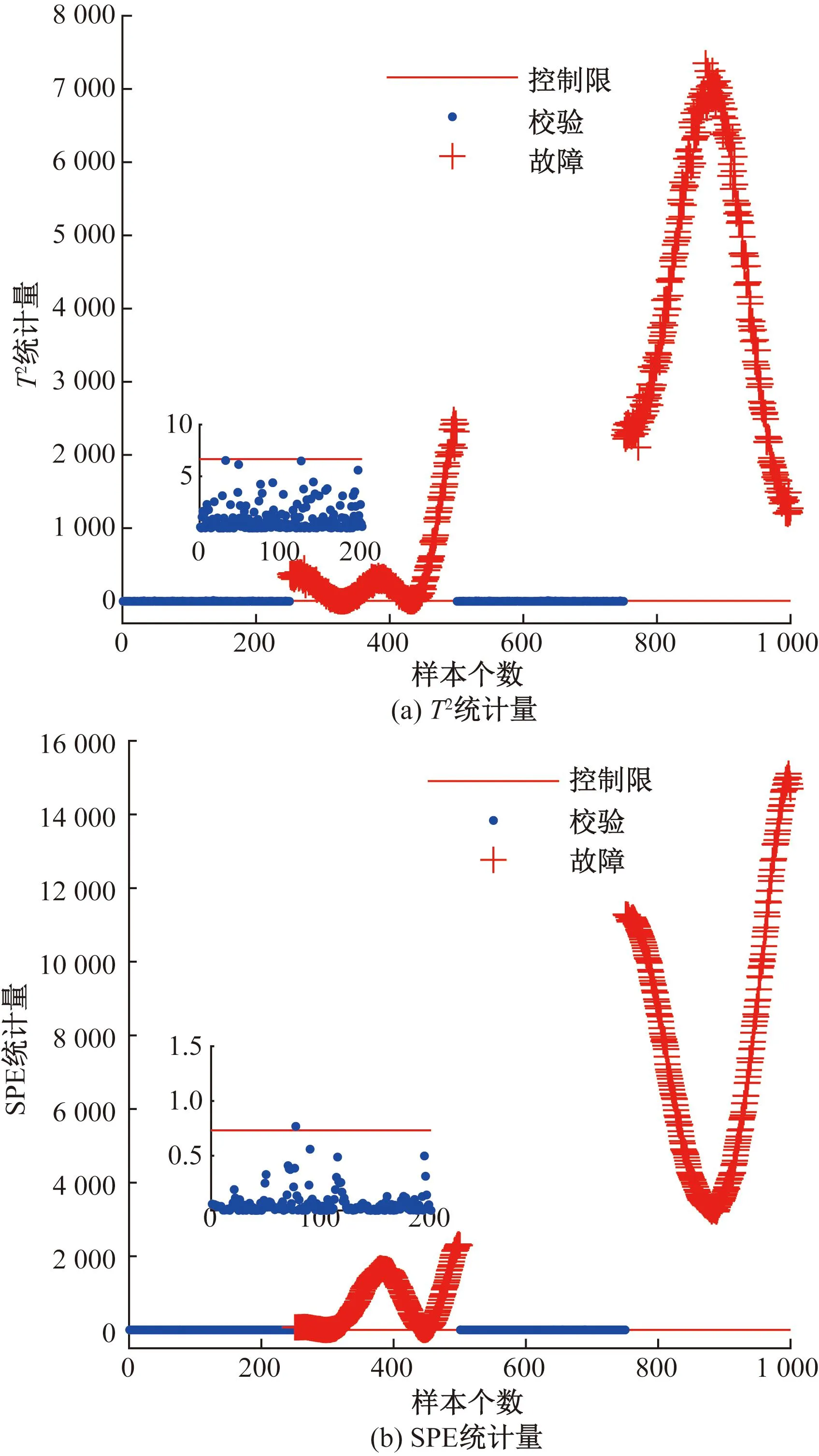
图7 数值例子DWDPCA故障检测图Fig.7 DWDPCA fault detection diagram for numerical examples

由图6可以看出,使用PCA方法进行故障检测检测效果很不理想,T2统计量的故障检测率为0,SPE统计量的故障检测率为6.2%。这是由于数据具有动态特性和多模态特性,使用全局建模方法计算得到的控制限指标过高,无法检测到故障。从图7可以看出,使用DWDPCA方法可基本将故障数据完全检测出来,T2统计量的故障检测率为96.4%,SPE统计量的故障检测率为98.8%,相比于PCA故障检测率提高了92.6%,具有较高的检测率。

2.2 TE过程故障检测

TE平台是根据多变量的复杂化工反应过程模拟的仿真平台,已被大量应用于检测故障诊断算法有效性的实验中。TE过程有5个操作单元和8种气体成分,共53个变量,由12个控制变量和41个测量变量组成,本实验选取41个测量变量用于故障检测。

TE过程根据生产物G/H的比例将生产过程分为4种模式,本实验选取模态1和模态3进行故障检测,具体如表1所示。系统先在模态一下运行48 h,然后再在模态三下运行48 h,期间以3 min为间隔进行采样,共采集训练样本1 920组。测试集数据的采集和上述方法相同,但均在每个模态运行8 h时加入不同类型的故障,直至本模态运行结束,故障说明如表2所示。

表1 TE过程生成模式Table 1 TE process generation models

表2 TE过程故障说明Table 2 TE process fault description

如图8和图9所示,任取两个变量分别绘制原始数据和经DWD方法处理后的数据散点图和分布图。由图8可知,原始数据为多模态结构,方差差异明显。经DWD方法处理后数据转化为单模态且近似服从单峰高斯分布,如图9所示。

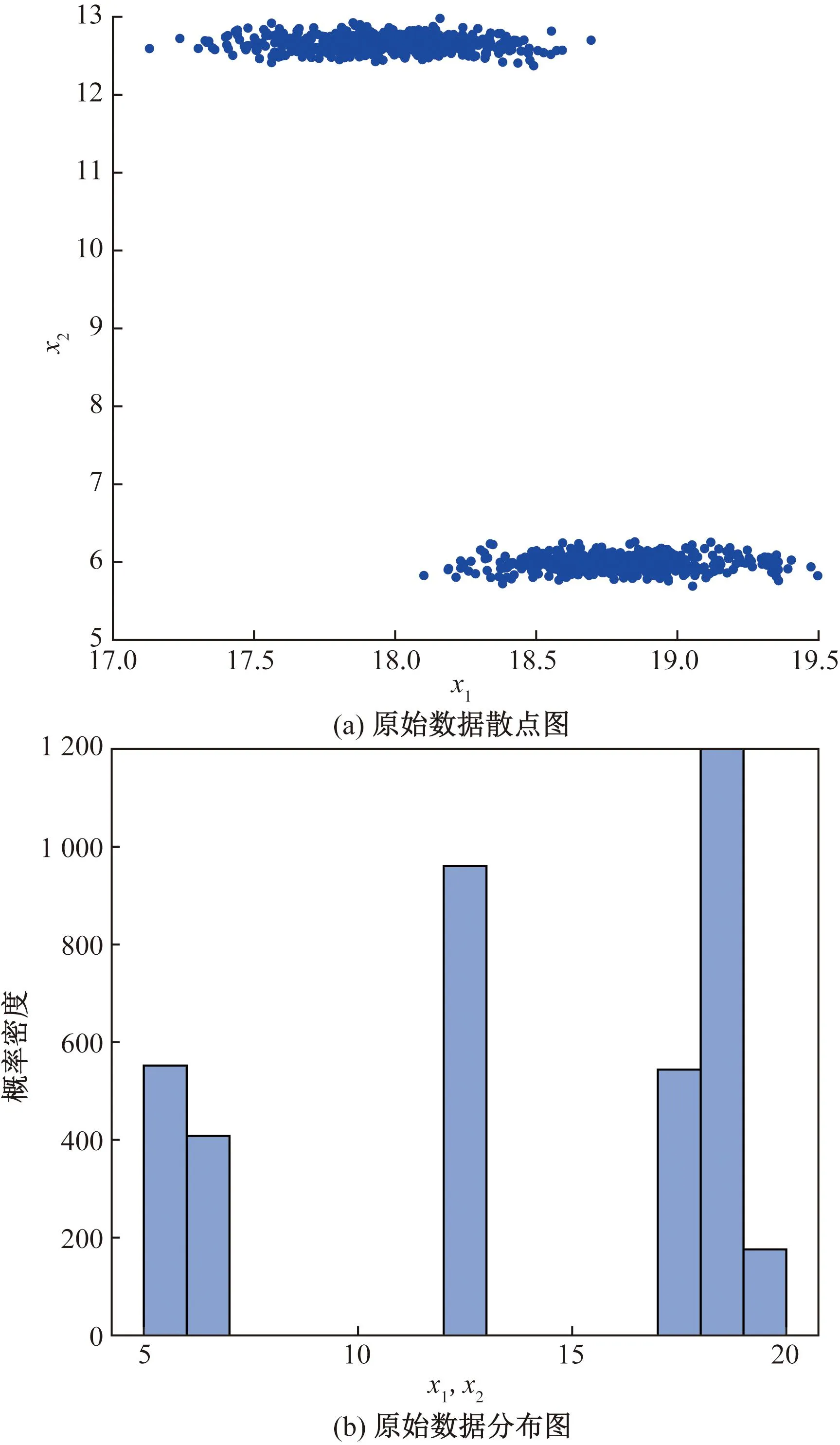
图8 TE过程数据散点图及分布图Fig.8 Scatter plot and distribution diagram of TE process data

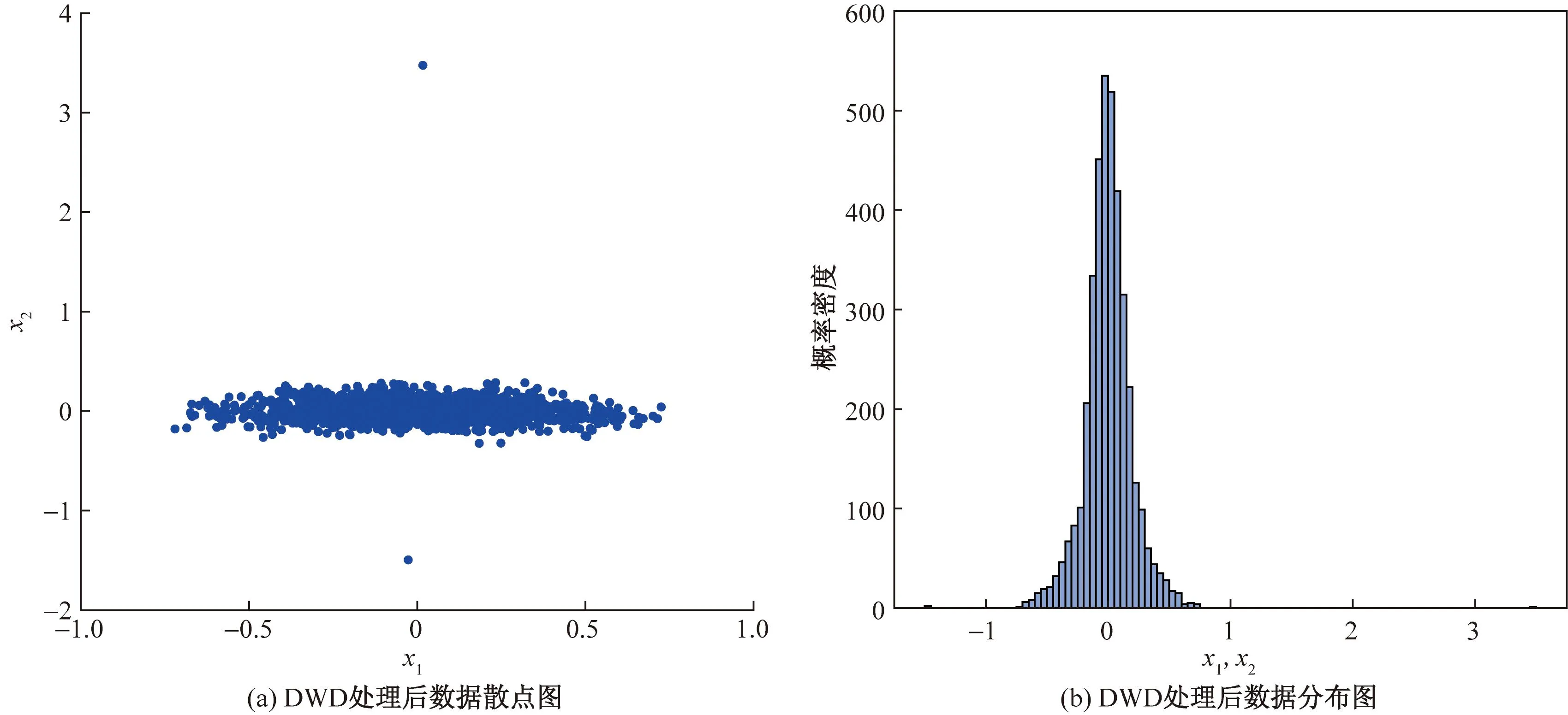
图9 TE过程DWD方法处理后数据散点图及分布图Fig.9 Scatter plot and distribution diagram of data after TE process DWD method

使用PCA和DWDPCA方法进行故障检测,置信度为99%,累计贡献率为85%,通过交叉验证方法确定DWDPCA的时间窗长度L为5,近邻数K为5。使用这两种方法对不同故障的故障检测率如表3所示。由表3可知,DWDPCA方法对6种故障的故障检测率均高于PCA方法,DWDPCA的故障检测性能得到验证。

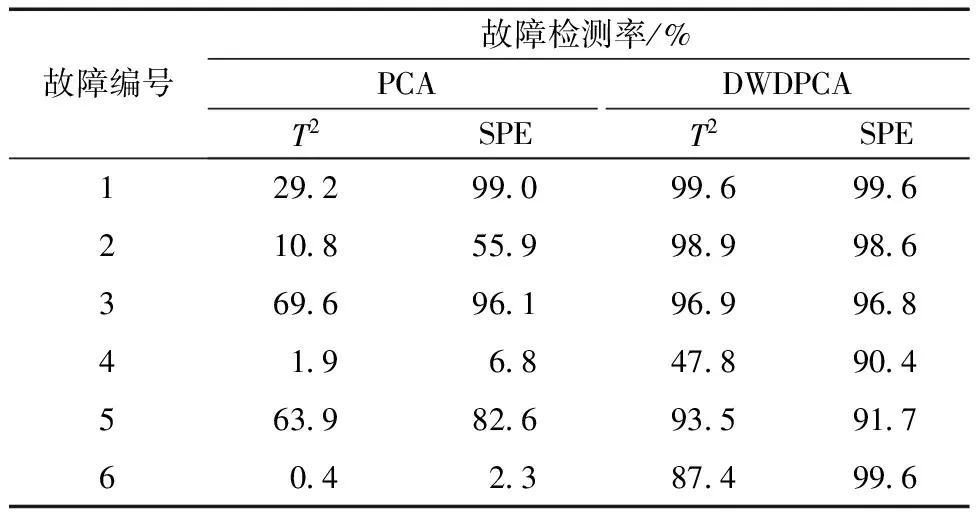
表3 测试集故障检测率Table 3 Test set fault detection rate

以故障2为例,A/C进料流比不变,组分B含量发生阶跃变化,致使总进料发生改变,使系统无法正常运行而发生故障。使用PCA和DWDPCA方法对此故障进行诊断,诊断结果如图10和图11所示。PCA的T2统计量的故障检测率为10.8%,SPE统计量的故障检测率为55.9%,DWDPCA的T2统计量的故障检测率为98.9%,SPE统计量的故障检测率为98.6%,相比于PCA故障检测率提高了42.7%。DWDPCA方法的故障检测效果明显高于传统PCA方法。这是由于DWDPCA方法首先对数据进行处理,消除了数据的时序特性和多模态特性,使数据符合使用PCA进行故障检测的前提条件,再使用PCA方法进行故障检测,使得检测性能得到提高。

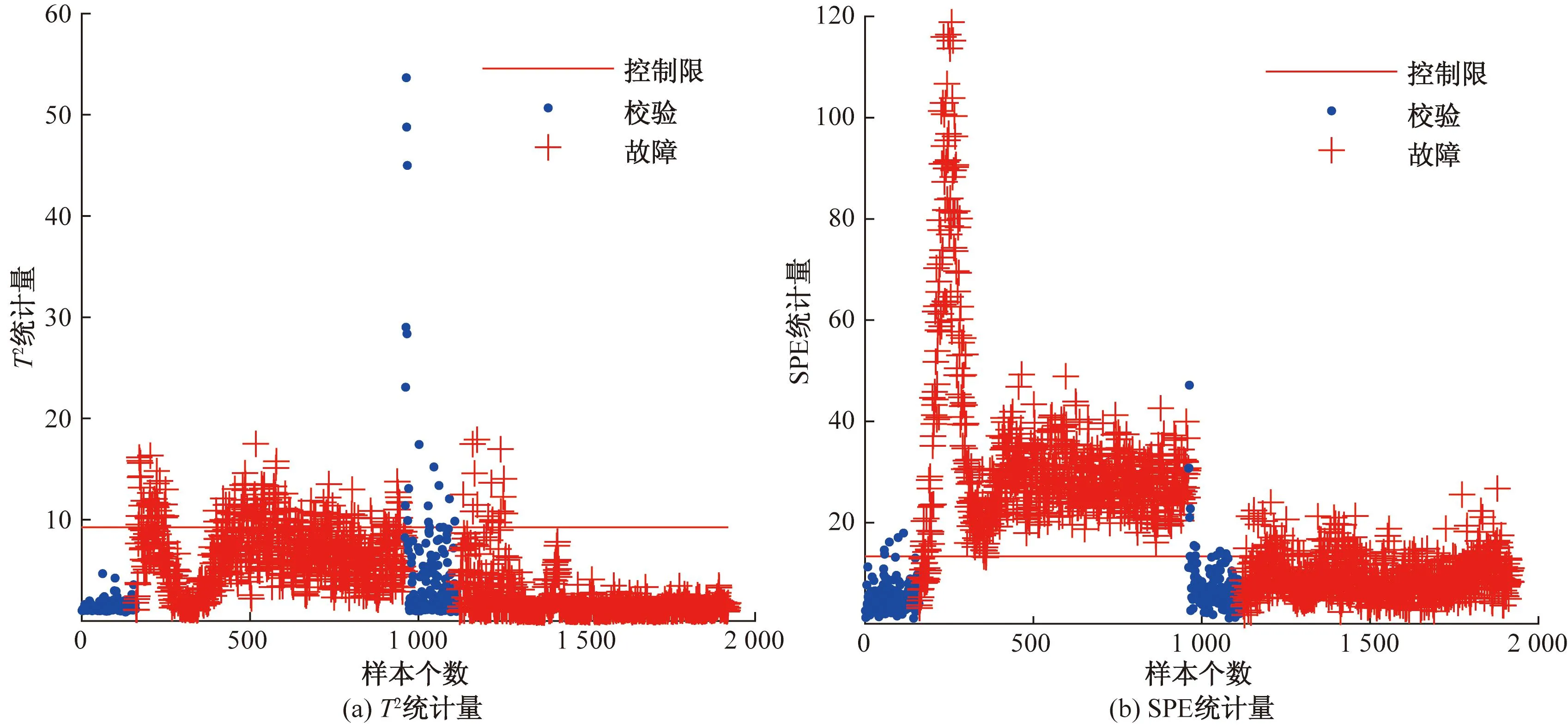
图10 TE过程PCA故障检测图Fig.10 PCA fault detection diagram of TE process

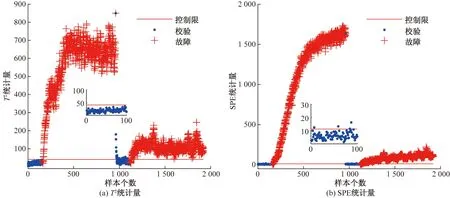
图11 TE过程DWDPCA故障检测图Fig.11 DWDPCA fault detection diagram of TE process

3 结论

针对工业系统中存在的动态特性和多模态特性问题,提出了DWDPCA故障检测方法。通过使用数值仿真例子和TE仿真平台进行故障检测可得出如下结论。

(1)使用动态加权差分方法,克服了动态系统多中心结构的缺陷,消除了数据的时序特性,并将数据转化为单一模态且近似服从单峰高斯分布。

(2)针对具有动态特性和多模态特性系统,所提出的DWDPCA方法可显著提高其故障检测率,并通过实验验证了该方法的有效性和优越性。