基于LPV-MPC的风电机组功率-载荷协调控制策略

梁栋炀，宋子秋，刘亚娟

（华北电力大学控制与计算机工程学院，北京 102206）

0 引言

风电机组大型化已经成为风电行业降本增效的主流发展趋势[1]。大型风机在提升发电容量的同时，也将导致更大的结构载荷。大型风机的变桨控制目标不仅仅是实现功率的稳定调节，还应当尽可能地降低结构载荷[2]。

风电机组是一个气动-伺服-弹性互相耦合的高度非线性系统，其变桨运行工况范围宽，受到外界风速波动影响大，这给风机变桨控制设计带来了巨大挑战。传统的风电机组变桨控制策略是基于发电机转速误差信号进行增益调度比例积分控制（GS-PI）[3]，但这种传统控制策略无法很好地处理系统约束，在靠近额定风速区间常常出现执行器饱和现象，导致控制性能恶化。为了解决约束问题，文献[4]建立了大惯量风机线性控制模型，采用模型预测控制（MPC）策略进行变桨操作，同时兼顾了功率调节和载荷降低性能，但该方法是基于单一工况点模型设计的，无法适应风机大范围变工况运行。文献[5]建立了风电机组简化的非线性模型，提出非线性MPC变桨控制策略，该控制策略能够有效克服风速扰动。但非线性MPC控制器设计困难，优化问题求解时间较长，难以实现实际应用。文献[6]采用Wiener模型所设计的PI和MPC控制策略能够取得良好的变桨功率调节控制效果，但该方法未考虑载荷优化，且尚未在风电专业软件OpenFAST上进行测试，其模型及控制器的有效性有待进一步验证。文献[7]建立了风电机组的模糊模型和线性参数变化（LPV）模型，采用MPC控制器实现了功率调节与结构降载荷。然而这些工作均是基于静态功率经验系数来获取线性模型，与实际风机气动性能有较大差距，且以上工作均未考虑塔筒动态，无法同时兼顾功率调节与载荷降低。

针对以上问题，本文采用机理与参数辨识相结合的方法，构建能够体现风机大范围变工况运行特性的LPV模型。引入间隙度量理论对局部线性模型进行分析，降低构建LPV模型的复杂度。对于实际风电机组状态不完全可测的问题，设计了时变卡尔曼滤波器实现风机的最优状态估计。基于获得的最优状态，设计自适应MPC变桨控制器，实现了大型风电机组功率-载荷协调控制。

1 风电机组模型

1.1 非线性模型

为了得到用于控制系统设计的风电机组模型，本文建立了包含气动、传动链、发电机、变桨执行器和塔筒的风电机组非线性模型。选取传动链扭转角θ、转子转速ωr、发电机转速ωg、变桨角度β、发电机转矩Tg，塔筒一阶前后弯曲位移dt和速度d˙t为状态变量，变桨指令βcmd和转矩指令Tg_cmd为输入变量，风速V为扰动输入，ωg和d˙t为实际可测量输出变量，则非线性模型的动态方程可以表示为

式中：f为系统状态；x=[θ，ωr，ωg，β，Tg，dt，d˙t]T；u为控制输入，u=[βcmd，Tg_cmd]T。

F为u和V的非线性函数向量，其线性部分见文献[8]，非线性部分可表示为

式中：Ng为齿轮箱增速比；Ks，Ds分别为传动链低速轴弹性常数和阻尼系数；Jr为转子惯性；Tr为气动转矩；Mt，Dt，Kt分别为塔筒一阶前后弯曲模态的等效塔顶质量、阻尼和刚度系数；d¨t为塔筒一阶前后弯曲模态的加速度；Ft为转子气动推力。

1.2 LPV模型

构建LPV模型首先需要获得被控对象的局部线性模型。前文获得的风电机组模型的主要非线性项为Tr（ωr，β，V）和Ft（ωr，β，V），将其在稳态工况点使用一阶泰勒展开公式进行线性化，可得：

式中：Δωr，Δβ，ΔV分别为转子转速增量、变桨角增量和风速增量；分别为转子转矩对转速、变桨角和风速的偏导数；分别为转子推力对转速、变桨角和风速的偏导数。

通过使用高保真风机仿真软件OpenFAST，固定NREL5MW风电机组的转子转速为12.1r/min，然后给定一系列11.4～25 m/s内的风速作为激励信号，并调整变桨角使得气动功率稳定在5.29 MW，可以唯一确定风电机组的稳态变桨角和塔顶位移（图1）。

得到了稳态工况轨迹后，通过在稳态点附近做小扰动线性化试验，使用差分扰动方法计算气动偏导数。

式中：Y为气动转矩Tr或气动推力Ft；y为转子转速ωr、变桨角β或风速V；Δy为在给定工况点处ωr，β或V的增量。

图2为辨识得到的NREL 5 MW风电机组的气动偏导数。

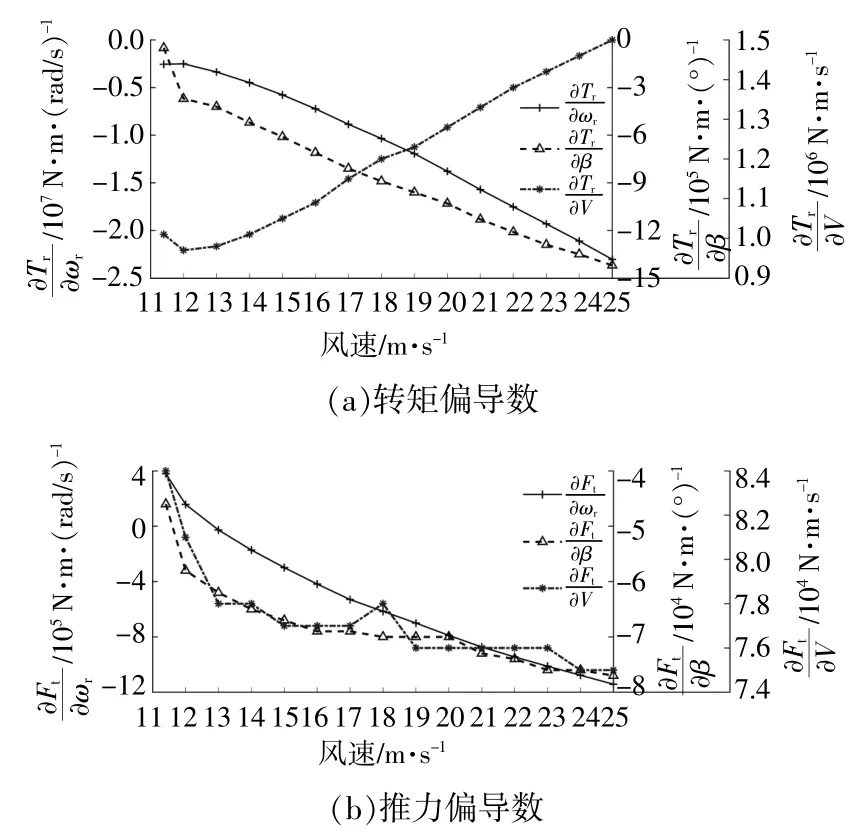
图2 气动偏导数Fig.2 Aerodynamic derivatives

由于可获取的局部线性模型过多，构建LPV模型所需的局部线性模型选取具有盲目性，本文引入间隙度量理论进行局部模型的选取。间隙度量理论用来度量两个线性动态系统之间的距离，对于i=1，2，带有右互质分解的两个传递函数Gi（s）[9]可以表述为

式中：Ni（s），Mi（s）均为Gi（s）的归一化右互质因式分解。

Mi（s）具有逆函数，并且Ni（s）和Mi（s）满足式（9）[9]。

式中：Ni（s）*，Mi（s）*分别满足Ni（s）*=Ni（-s）T和Mi（s）*=Mi（-s）T；I为单位矩阵。

传递函数G1（s）和G2（s）之间的间隙度δ[G1（s），G2（s）]可定义为

间隙度的取值为δ[G1（s），G2（s）]∊[0，1]。通过预设合理的间隙阈值δth，选取最优数量的局部线性模型可以降低构建LPV模型的复杂度。在风速为12～25 m/s，以1 m/s为风速间隔，计算桨距角输入βcmd到发电机转速输出ωg的传递函数之间的间隙值，结果如图3所示。

图3 线性模型之间的间隙度Fig.3 The gap value between linear models

图中，G12～G25分别表示风速为12，13，…25 m/s时，输入βcmd到输出ωg的传递函数选取合适的间隙阈值δth=0.2[8]。最终，简化得到风速为12，15，19 m/s和25 m/s的4个局部线性模型。

选取可测量风速V作为LPV模型唯一的调度变量ρ（t）。调度空间定义了调度变量V的变化值为12～25 m/s。

LPV模型的调度规则采用线性内插法和最近邻外插法，最终得到的LPV模型为

式中：Ac，Bc，Bcv，Cc分别为连续的状态增益矩阵、控制增益矩阵、扰动增益矩阵和输出增益矩阵。

2 自适应MPC变桨控制器设计

图4为设计的整个变桨控制策略原理图，包含风电机组LPV模型的构建、自适应MPC控制器和时变卡尔曼滤波器的设计。

图4 基于LPV模型的自适应模型预测变桨控制结构图Fig.4 Structure diagram of adaptive model predictive pitch control for wind turbine based on LPV model

2.1 自适应MPC控制器

2.1.1预测模型

自适应MPC控制器的预测模型为以上建立的LPV状态空间模型，取采样时间为Ts，使用前向欧拉法进行离散化可得到离散LPV模型。

式中：Ad，Bd，Bdv，Cd均为离散化的系统增益矩阵。

在每个采样间隔，LPV模型根据当前调度变量更新预测模型，更新后，Vˉ（k+i）=Vˉ（k），∀i∊[0，Np-1]表明在整个预测时域内调度变量保持不变。x（k）=x^（k|k）表示系统状态由时变卡尔曼滤波器进行估计。

2.1.2代价函数

自适应MPC控制器的代价函数[10]可表示为

式中：ep=x（k+Np|k）-xref为终端状态误差，xref为参

2.1.3系统约束

由于风机变桨执行机构的物理限制，需要在控制问题中考虑风电机组变桨执行器约束，具体可表示为

式中：βmin，βmax分别为变桨角允许的最小值和最大值；βth为变桨执行器单位时间内的最大变桨角度。

在每个控制时域，自适应MPC变桨控制动作均需满足变桨角幅值和速率的约束。

2.1.4优化求解

在每个控制间隔，自适应MPC在线求解约束二次规划问题。

使用有效集方法对以上优化控制问题进行求解。Uk=[u*（k|k），u*（k+1|k），…，u*（k+Np-1|k）]T是在预测时域为Np时得到的最优控制序列。

2.2 时变卡尔曼滤波器

然后，使用测量值y（k）更新估计状态。

在下一个递归过程中需要进一步更新误差协方差矩阵Pk，直到卡尔曼增益和误差协方差矩阵稳定并保持常数。

式中：Q为测量噪声协方差矩阵。

3 仿真结果与分析

以NREL 5 MW风机为参考机组，关键参数见表1。

表1 NREL 5 MW风机的关键参数Table 1 Key parameters of NREL 5 MW wind turbine

在OpenFAST和Matlab/Simulink平台上进行联合仿真测试，验证LPV模型的精度和控制器的有效性。仿真过程中激活风机所有可用自由度。仿真环境的硬件配置为CPU i7-7700HQ，2.80 GHz和8 GB内存的计算机。

仿真的相关控制参数设置如下：比例因子能够使每个状态变量划归为同一数量级，权重的调整更加注重于相对重要性，根据每个状态变量的变化范围来确定，未知变化范围的变量设置为1。本文比例因子设置为Sx=diag（[0.004 8 1.267 122.910 30 0.4 1]），Su=1，终端权重矩阵P在每个时刻通过求解无约束最优控制问题的黎卡提微分方程得到[10]。根据相关经验，权重矩阵采用多次仿真迭代测试进行配置，设置为Q=diag（[0.3 0.1 2 0 0 0.01]），Ru=0和RΔu=0.05，采样时间与OpenFAST软件推荐的采样时间保持一致Ts=0.012 5 s。考虑MPC求解的稳定性和复杂性，预测时域设置Np=15。

3.1 LPV模型验证

将NREL 5 MW完全非线性风机模型、18 m/s风速处的局部线性模型和本文提出的LPV模型进行开环响应对比，以此验证LPV模型的准确性。采用阶跃变化的风速（12，14，16，…，24 m/s），分别比较3种模型的发电机转速和塔筒一阶前后弯曲位移响应，对比结果如图5所示。

图5 LPV模型验证Fig.5 Validation of LPV model

由图5可知，在远离稳态工况时，18 m/s局部线性模型系统动态响应与NREL 5 MW相差较大，这是由于风机的非线性较强，单一的线性化模型只能够在其稳态点附近与非线性模型有较好的一致性，而LPV模型可在风速大范围变化时仍然与NREL 5 MW风机模型开环响应曲线有很好的一致性。为量化开环响应的误差，采用平均绝对百分比误差（MAPE）指标来进行分析。结果显示：18 m/s风速处的局部线性模型与NREL 5 MW完全非线性模型的发电机转速开环响应MAPE为6.81%，塔顶弯曲位移的MAPE为6.52%，两者差距较大；本文建立的风电机组LPV模型与NREL 5 MW完全非线性模型的对应指标分别为0.46%和5.47%，表明本文建立的风电机组LPV模型精度可以达到后续自适应MPC控制器的设计需求。

3.2 自适应MPC控制器仿真分析

采用突变风和阶跃风，与GS-PI控制和普通MPC（18 m/s单一模型MPC）控制策略进行对比，对本文提出的基于LPV模型的自适应MPC控制器（LPV-MPC）的有效性进行验证。使用IECWind软件[12]产生突变风，风速设置及控制仿真结果如图6所示。

图6 GS-PI，MPC与LPV-MPC控制器性能对比Fig.6 Performances comparison between GS-PI controller MPC controller and LPV-MPC controller

由图6可知，在突变和阶跃风速下，本文提出的基于LPV模型的自适应MPC控制器能够及时调节叶片进行变桨动作，降低突变风速下的功率波动峰值和载荷峰值，在接近额定风速时，自适应MPC能够考虑系统约束，进行最优变桨调节，既降低了调节时间和超调量，又避免了执行器饱和，可有效防止控制性能恶化。

相比于普通MPC（18 m/s单一模型MPC）控制器，LPV-MPC在高风速和靠近额定风速区间时显示出更好的控制性能，主要表现为降低了功率波动的超调量和减少了调节时间，同时降低了载荷峰值。为了使得控制性能对比更加明显，采用平均值和标准差对控制结果进行量化，结果如表2所示。

表2 仿真结果量化分析Table 2 Quantitative analysis of simulation results

由表2可知：普通MPC控制策略的功率平均值与变桨角度偏差最大，同时塔基载荷标准差最大，其主要原因是偏离18 m/s额定工况时，风机的非线性使得模型失配，导致控制性能下降；LPV-MPC控制器使发电功率更加平稳，功率平均值更加接近5 MW，相比于GS-PI控制器，功率波动降低了36.57%，载荷波动降低了26.27%；变桨控制动作功率平均值增大了0.68%，波动降低了29.6%。这说明本文所设计的基于LPV模型的自适应MPC控制器能够在风速大范围变化时，充分利用风电机组变桨约束条件，做出最佳变桨控制输出，同时兼顾了功率调节与载荷降低性能。

4 结论

针对大型风电机组功率-载荷协调控制，本文提出了一种基于LPV的风电机组模型，采用自适应模型预测控制算法在线求解最佳变桨控制动作，实现了大型风机功率-载荷协调变桨控制。

①借助OpenFAST软件，使用差分扰动方法可以计算得到更加精确的风机气动偏导数。采用间隙度量理论能够有效指导风机局部线性模型的选取，使构建的LPV模型的模型库数量由14个降为4个。

②与NREL 5 MW非线性风机模型相比，本文建立的LPV风机模型的发电机转速和塔顶弯曲位移开环响应的平均绝对百分比误差分别为0.46%和5.47%，该LPV模型可以反映大型风电机组的非线性动态特性，能够满足先进控制器的设计需求。

③在突变和阶跃风速下，与常规PI控制器与传统MPC控制器相比，自适应MPC控制器能够在每个采样时刻跟随风况变化，更新预测模型，通过权重矩阵的衡量和约束优化问题的求解，自适应MPC控制器能够做出最佳变桨控制动作，降低了功率波动幅度和调节时间，同时降低了塔基载荷均值和波动幅度，实现了功率-载荷协调控制。