含软弱夹层场地的一维等效线性化地震响应研究

唐俭政 张 齐 黄颖婷 崔如玉 彭 刚

(1.防灾减灾湖北省重点实验室(三峡大学), 湖北 宜昌 443002;2.三峡大学 土木与建筑学院, 湖北 宜昌443002)

我国地震区域广阔而分散,地震发生的场地类型多样而复杂[1].根据海内外学者对众多地震区域震后情况的统计研究发现,地震区域的场地条件对地震引起的破坏类型和程度有重要影响[2].而普遍存在于各类地形地貌中具有较小的剪切模量和较大变形能力的软弱夹层会使得场地的基本自然周期延长,且通过夹层后的地震波频谱特征也会发生改变,在特殊情况下可能与上部结构形成“共振”效应,从而使得场地和上部结构产生异常的破坏,如在地震作用下的边坡场地由于存在软弱夹层导致稳定性不足而引起的滑坡、泥石流灾害等;地下岩石场地中存在较脆岩层导致局部强度不足而引起的土地开裂等;地基场地或路基下存在较软弱夹层导致承载力过小和变形不均匀引起的不均匀沉降等[3].

正常状态下,场地土层具有连续性和稳定性,软弱夹层不会轻易引起场地及结构的失稳与破坏,而在动力作用时,相对于建立在岩石或硬土上的结构,建立在软土场地上的结构则会发生较大、较快的破坏.这是由于软弱夹层在较小的外力作用下也会有较大的土壤变形,从而引起场地失稳和上层结构破坏,如肖景文等[4-5]对含软弱夹层的场地上路堤桥台的地震响应进行了研究,发现离软弱夹层越近的路堤沉降和位移产生更加快速和显著.以往研究还表明,场地中的软弱夹层对地震波在场地中具有减小加速度和消耗能量的作用,会使地震波传输到地表的能量减小,从而减小传输到地表的地震对上部结构的破坏与影响[6-7],如温卫平等[8]通过数值模型分析了含软弱夹层的子盆地和小山包的地震响应特征和PGA 变化规律,发现软弱夹层的存在使得盆地地表PGA 减小.此外软弱夹层对地震动特征、场地以及上部结构也有所影响,如Villalobos M 等[9]通过对日本软土实地的地震动响应分析与研究计算指出:软土在地震作用下会使得加速度的频谱在软弱场地自然频率附近出现放大;张日新[10],曹均锋等[11]使用等效线性化方法对含不同特征的软弱夹层场地和上部高层建筑结构进行了地震响应对比研究,发现不同厚度和埋深的软弱夹层影响了地表和上部建筑结构的动力响应;王冲等[12]采用数值模拟的方式研究了软弱夹层对场地中加速度传递以及场地特征周期的影响;闫孔明[13-14],左熹[15],曹杰等[16]采用离心振动台试验,研究了软弱夹层对加速度放大效应、频谱特征、土体受力与位移的影响;杨乾等[17]基于ADINA 分析了不同特征量的软弱夹层对场地中的管道地震动响应的影响;刘汉香等[18]通过施加不同激振强度的地震动对含不同相对高程、不同厚度以及不同倾角软弱夹层的斜坡模型的振动台试验,分析研究了这三类夹层特征对边坡的地震响应及破坏形式的影响.

综上所述,目前针对软弱夹层场地地震反应研究成果主要侧重于对地表地震响应特征的比较和基于经验数据的场地放大效应模型构建.而从土体剪切应变变化规律的角度分析软弱夹层对场地地震响应特性和场地放大效应的影响规律和机理的研究尚不充分.因此,本文通过计算不同地震工况下的含软弱夹层场地地表响应,分析了软弱夹层对地震动频谱特性和场地放大的影响规律,并根据土层应变计算结果研究了土体的剪切模量和阻尼变化,从软弱夹层对地震波能量耗散和吸收作用的角度对上述规律进行了解释.揭示了不同工况下软弱夹层对场地地震响应的影响规律,探明软弱夹层对场地地震响应的影响机理,为地震灾害的预测、防范和减灾提供了理论参考.

1 计算模型

1.1 研究方法及场地模型

一维场地响应分析被用来解决水平剪切波(SH波)在水平分层土壤中的垂直传播问题,波传播方程的解决过程是在频域中进行的.在计算模型中水平土层的行为被近似为Kelvin-Voigt固体,其中弹性剪切模量和黏性阻尼是土壤的属性特征[19].一维模型的等效线性化研究方法无需考虑土层间的接触关系和场地边界条件的设置,且其原理是在总动力学效应上通过等效意义下的剪切模量和阻尼比代替非线性变化下的所有不同应变幅值下的剪切模量和阻尼比,将非线性问题转化为线性问题进行计算[20].此方法方便快捷,能够极大地节省计算时间,并能得出相对准确合理的结果,如Shylamoni P 等[21]使用等效线性化方法对日本柏崎刈羽核电站进行了一维等效线性地震反应分析,结果表明等效线性化的计算结果与现场的大多数余震记录值有很好的一致性.

本文对地震波在场地中的传播的模拟是用一维场地分析程序EERA[22]进行的,它是为了模拟地震在地下土壤中的传播而开发的,采用修正的Hardin-Drnevich模型,并具有等效线性分析的特点.首先基于动剪切模量曲线(G/G0-γ)和动态阻尼曲线(ζγ)来进行土壤的剪切模量和阻尼参数赋予,淤泥质土(软弱夹层)的两种模量曲线如图1所示.

图1 动剪切模量曲线与动态阻尼曲线

基本场地模型是运用计算软件EERA 所构建的深度为78 m 的含2 m 软弱夹层的一维基础场地模型,默认场地下部为坚硬基岩,基岩剪切波速为1 000 m/s,满足我国规范规定[23]岩石层剪切波速大于500 m/s的要求.岩层上总共由9种土质组成,动剪切模量以及阻尼参考袁晓铭[24-25],Sun J I和Seed H B等[26]研究所得出结果进行选用,场地土层结构及剪切波速如图2所示,基本场地内土层结构属性见表1.

表1 场地土层结构参数表

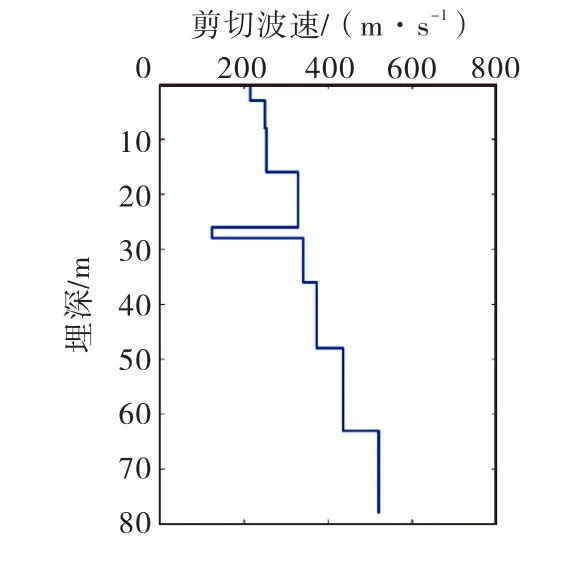
图2 土层结构及剪切波速

1.2 地震动输入与计算

场地模型可能经受的以及各类实际场地可能遇见的各种地下运动是场地预测分析的主要未知数,运动的幅值、总时长、震动频率、震源位置以及运动路径等都对场地以及地面结构的运动和破坏有影响.由于地震本身的偶然性且部分未知参数不能准确确定,本文所进行的研究为满足地下基岩地震动输入的合理性,依据基岩剪切波速(1 000 m/s)和基岩深度(78 m)从Kki-net地震记录数据库中选取符合基本条件的3种不同地震波,编号分别记为A 波、B 波和C 波.为在满足计算需求的前提下节省计算时间,截取地震波主要部分,截取地震动与原始地震动速度时程部分见下图,时长均为40 s,截取地震加速度与原始地震加速度基本一致.计算其傅里叶频谱观察地震波频谱特征.选用的地震波加速度时程曲线以及傅里叶谱曲线如图3～5所示.

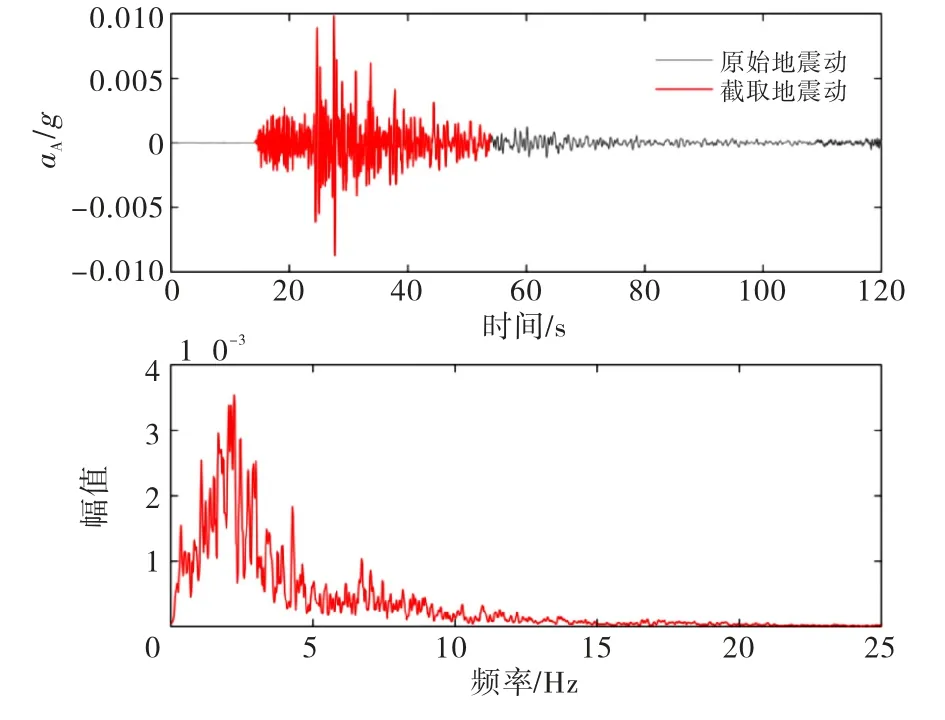
图3 A 波加速度时程和Fourier幅值谱

图4 B波加速度时程和Fourier幅值谱

图5 C波加速度时程和Fourier幅值谱

此次数值模拟计算了基岩处输入地震动幅值变化时的场地地震响应.记录场地地表和软弱夹层上下位置处的加速度时程并计算了其傅里叶谱,之后进行场地地震响应对比以分析软弱夹层对场地的地震响应影响,此过程通过与基岩处的PGA 进行对比计算放大系数k以及对应的Fourier谱值比r来进行说明,计算过程如下.

式中:PGAsurface是地表处的加速度峰值;PGAinput是基岩处的输入加速度峰值;Fsurface是地表加速度的Fourier谱值;Finput是基岩输入加速度的Fourier谱值.

2 计算结果分析讨论

2.1 基岩输入对软弱夹层场地放大的影响

观察基岩输入PGA 从0.05g到0.5g的3种地震波在含有软弱夹层和不含软弱夹层的基岩上场地时地表的PGA 放大系数k=PGAsurface/PGAinput变化,如图6～7所示.

图6 无软弱夹层场地地表PGA 放大系数随输入地震强度变化曲线

从图6可看出,当场地中未含有软弱夹层时,地表的PGA 放大系数是普遍大于1的,意味着地震波穿过场地后到达地表的地震动增大.而图7中含有软弱夹层的场地地表PGA 放大系数明显小于图6中的数值,且在输入地震PGA 大于0.1g时系数是小于1的.可得出结论:软弱夹层的存在使得地表加速度明显减小,在经受较大地震强度时,地表加速度的幅值小于输入地震动,这与曹均锋等[11]的研究结论相似.

图7 含2 m 软弱夹层场地地表PGA 放大系数随输入地震强度变化曲线

2.2 软弱夹层对地震频谱的影响

场地中不同的土层结构决定不同的土层性质,在动力计算中通常以场地基本自然周期和自然频率来表达.对于层状土,当基岩上的均匀土壤覆盖层具有恒定的剪切波速度时,场地的基本自然周期T n可定义为:

式中;H是高度;Vs是基岩上等效剪切波速度.

对于由明显不同土壤性质的若干土层组成的场地覆盖层,通常用覆盖层的等效剪切波速度Vs来计算整个沉积物的基本周期.则m层的场地等效剪切波速度可用式(4)计算:

式中:h i是第i层的均匀厚度;(Vs)i是第i层剪切波速度.

通过公式(3)、(4)联立,可计算出场地剖面的基本自然周期,基本自然频率被计算为基本自然周期的倒数.基于上述描述,表1中所描述的基本场地的基本自然周期和频率分别被评估为0.925 s和1 Hz.

场地有其基本频率,而频谱是波在单自由度(SDOF)系统中与自然频率(或自然周期)和阻尼比的函数,是描述SDOF系统对特定输入运动的最大响应[27].因此可通过对基岩与地表的频率谱值比曲线进行分析来讨论这上述地表加速度出现减小的原因.

在通常情况下,地震波在土壤中的传播的过程中会使地震波出现一些频段波的变化,这种变化可能是由于某种土质影响的,且高于土层或场地自然频率的波会使得部分土体在场地中产生移动[28].因此为探明场地中的土体对不同频率的波的敏感性而对在0.1g、0.2g、0.3g输入激振强度作用下不同地震波作用在表1基本场地时的傅里叶幅值比曲线来进行响应分析,如图8～9所示.

图8 0.1g、0.2g、0.3g 地震输入下无软弱夹层场地的地表与基岩的傅里叶谱值比

从图8、9对比看出,地震波在场地基本频率附近的频段波均被放大了,相比于无软弱夹层的场地地表的加速度频谱,软弱夹层的存在使得高频波段大幅度减小,而部分频率波段无论是否存在软弱夹层变化均较小,谱值比也较为稳定,这可能是因为此场地对个别频率的波段不敏感造成的.总的来说能得出这一相关结论:场地的自然属性对地震响应有所影响,使得地震波在场地中作用时接近场地自然振动频率的波段成分会增大,而软弱夹层的存在使得地震波中的高频成分极大的减少,能够达到消减传输到地表地震波的能量的作用,而最终使得到达地表的加速度减小.

2.3 软弱夹层场地效应机理分析

除频谱的变化外,软弱夹层处的PGA 和剪切应变也发生了较大变化,如图10～11所示.

在地震波经过软弱夹层后,加速度明显变小,软弱夹层中的发生的剪应变远大于邻近正常土层中的剪应变,这一不和谐的应变现象和刘[29]和Villalobos M 等[9]的对软土层的研究结果相似,软弱夹层在较小地震作用下都产生了与其他土层相比不和谐的剪切应变.

由应力-应变滞回理论,土体耗散的能量随阻尼和应变的变化曲线可以用公式(5)中来表达.

式中:WD为耗散的能量;ξ为阻尼;γc为应变量.

这意味着土壤变形增大消耗了地震波的能量从而使得穿过软弱夹层之后的地震PGA 变小,是符合基本力学理论的.因此可以得出结论:软弱夹层应变增大的过程中地震的加速度减小,认为软弱夹层的变形有消耗地震能量的作用,但土壤的变形增大,可能导致场地的位移和应变增大,因此这可能对工程结构造成严重破坏,应着重注意.

从图10～11可以看出,另外一个较为明显的特征是,虽然地震波B的输入PGA 和A 波,C波一样,但是其在软弱夹层下部的地震PGA 明显小于A 波和C波,引起的软弱夹层的剪切应变量也明显小于A波和C波,观察软弱夹层上下处的3种地震波的频谱图发现,B波的10 Hz附近的频段成分较多,而通过图8、图9发现场地对此频率附近的波段不敏感,因此导致B波在土层中引起的加速度响应变化和软弱夹层剪切应变都较小.

图9 0.1g、0.2g、0.3g 地震输入下含软弱夹层场地的地表与基岩傅里叶谱值比

图10 0.1g、0.2g、0.3g 地震输入下的各土层表面PGA

图11 0.1g、0.2g、0.3g 地震输入下各土层最大剪切应变

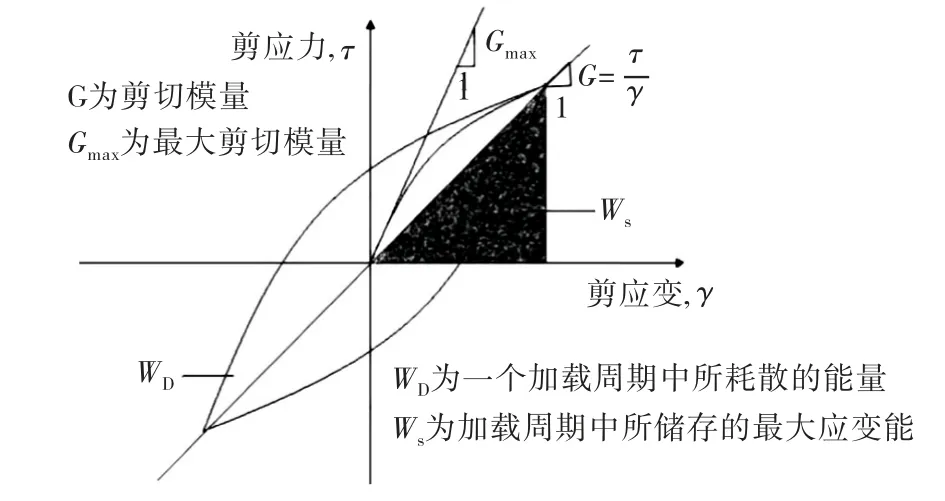
图12 应力-应变滞回曲线

根据上述研究结果,软弱夹层土具有相当程度的消耗地震能量的作用和较大的压缩性,相对较低的运动强度(0.1g)也使得土体产生了相对此场地其他土体来说相当大的剪切应变.与具有较大阻抗比的土壤相比,软弱土质产生的剪应变相对较大,剪切模量与阻尼比变化也较明显,如图13所示.其产生较大变形和消减高频波的性质是与其剪切模量减小和阻尼比增大有关的.

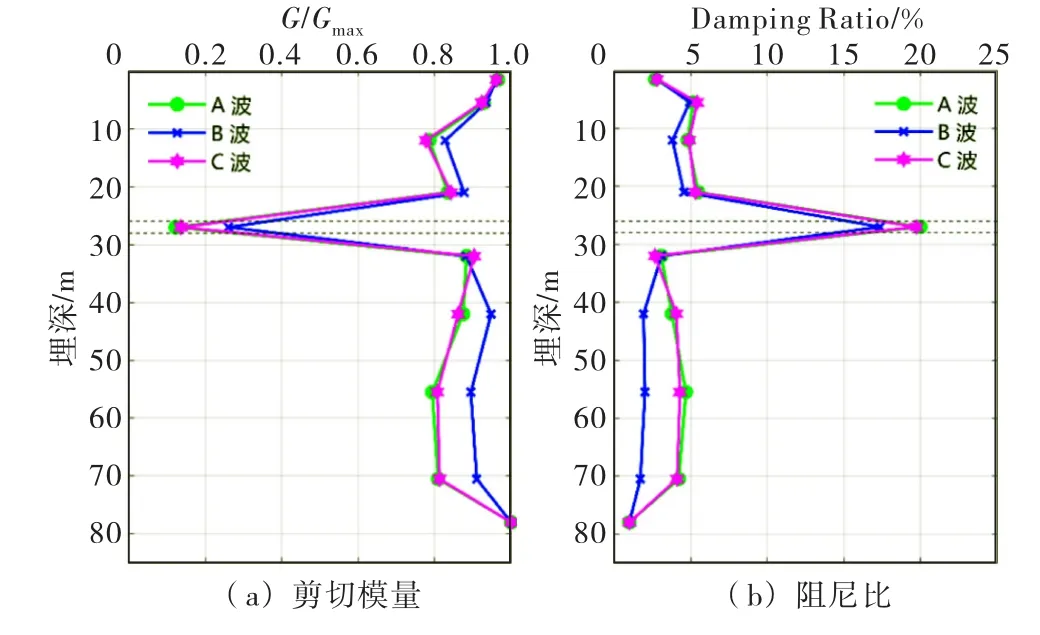
图13 0.1g 地震输入下的土层动剪切模量与阻尼比变化

基于上述分析结果以及其他学者的一些研究结论,可以了解到,虽然等效线性化计算软件(如EERA、SHAKE等)进行的一维线性地面响应分析被广泛用于描述地面响应的特征.然而,等效线性响应分析是一种保守的方法,因为它仅是在线性框架内接近非线性行为,而不能准确描述非线性土体的应力-应变关系[30].且其主要限制是在整个一维场地分析过程中使用了保持了相对恒定的阻尼和线性剪切模量,而未能体现实际动力运动中不同土体之间的具体非线性变化,因此等效线性地面响应分析会导致对软土层的峰值加速度和场地应变的高估.考虑到使用地震加速度时程在软土层处造成的较大剪切应变,且为降低这种不和谐的剪切应变,本文建议使用位移时程或力时程而不是加速度时程来施加作用可能更好的表现软弱夹层的应力应变响应,而此种操作超出了EERA 的适用范围,因此可以考虑运用其他程序来进行相关计算,本文仅说明软弱夹层对场地的地震响应的影响分析,不做后续研究分析.此外,等效线性地面响应分析可能会受到岩土工程现场条件的高度影响[31],对岩土工程条件的描述程度能够很大程度上影响计算的可靠性,且岩土工程场地土质属性的不时变化也会导致结果的显著变化[32],因此场地条件和土层属性的准确描述也至关重要.

3 结 论

通过上述分析,可以得出以下相关结论:

1)相比于无软弱夹层的场地,软弱夹层的存在使得地表PGA 显著减小,当输入地震PGA 大于0.1g时,软弱夹层使得地表PGA 放大系数小于1;并且软弱夹层在相对较低的地震强度(0.1g)作用下软土层就足以产生相对较大的剪切应变.

2)由于场地自然属性的原因,地震动在场地传递过程中场地自然振动频率附近的波段会明显增大,但地震动经过软弱夹层后其高频段的能量被减少,所以认为软弱夹层在场地中具有相当程度的滤波耗能作用.

3)根据剪切模量与应变变化的关系,软弱夹层的剪切模量变小是导致软弱土产生较大剪切应变的主要原因,并伴随着软弱夹层阻尼比的增大,而土层这种较大的土壤应变和较大阻尼则是软弱夹层消耗地震能量的主要原因.

4)考虑到软土层在较小的地震加速度时程作用下会出现的较大的不和谐剪切应变,建议使用位移或力时程来进行分析,这对软弱夹层地震响应分析可能会有更好的效果.