基于等效静载荷法的挤压铝门槛梁非线性结构优化

高伟钊 邓清源 杨军 潘锋

（1.迅仿科技（上海）有限公司，上海 201821；2.广州汽车集团股份有限公司汽车工程研究院，广州 511434）

1 前言

电动车动力电池常布置在车身地板下方，与车身扭力盒、左右侧门槛梁和地板等结构相连。为降低由车辆碰撞引起的动力电池起火、爆炸等安全事故发生几率，C-NCAP 管理规划（2021 年版）中的侧面碰撞工况对电动车采用更为严苛的32 km/h 侧面柱碰撞[1]。车身门环区域中的门槛梁结构在侧面柱碰撞工况中对电池包起主要保护作用，燃油车常采用高强钢或热成形冲压件与加强件的组合方案提升侧面耐撞性，然而钣金结构在腔体Y向空间利用率低，结构方案通常较重，挤压铝型材截面形式在碰撞方向上具有更大的设计自由度，抗弯和吸能特性优异，轻量化效果显著，成为电动车门槛梁结构的首选方案。

挤压铝门槛梁零件截面路径选型时，国内主流整车研发团队多基于经验或典型结构，采用试错法开展性能驱动下的筋板料厚设计，传统设计理念缺乏理论指导，结构方案的质量、成本和性能难以达成最优。针对于这一问题，国内外学者开展若干尝试，冯富春等采用变密度线性拓扑优化技术改进了某电池包挤压铝框架在侧挤工况下的截面形式[2]；易广威等提出了以线性拓扑优化技术为基础，混合元胞自动机非线性拓扑优化技术为补充的联合优化技术，在钢包铝门槛梁结构设计中开展了侧面柱碰撞工况下挤压铝门槛梁填充件的截面优化工作[3]；除此之外，Kathrina 等基于等效静载荷法（Equivalent Static Load，ESL）的非线性拓扑优化技术，对挤压铝横梁开展了类似研究，均取得较好效果[4]。

相关文献并未给出挤压铝结构截面路径选型和料厚优化的完整解决方案。为解决这一问题，基于等效静载荷梯度法优化技术，以某乘用车简化门槛梁结构为例，系统探索了挤压铝门槛梁结构正向优化设计的技术路线。

2 等效静载荷法与ESLDYNA软件

2.1 等效静载荷法基本原理

等效静载荷结构优化方法最早由B.S.Kang 于2001 年提出[5]，用于解决大变形碰撞非线性工况下的结构优化问题。碰撞工况CAE 求解常采用显式计算方法，求解过程中，系统中各零部件节点位移场在不同时刻有不同分布形式，如图1 所示。

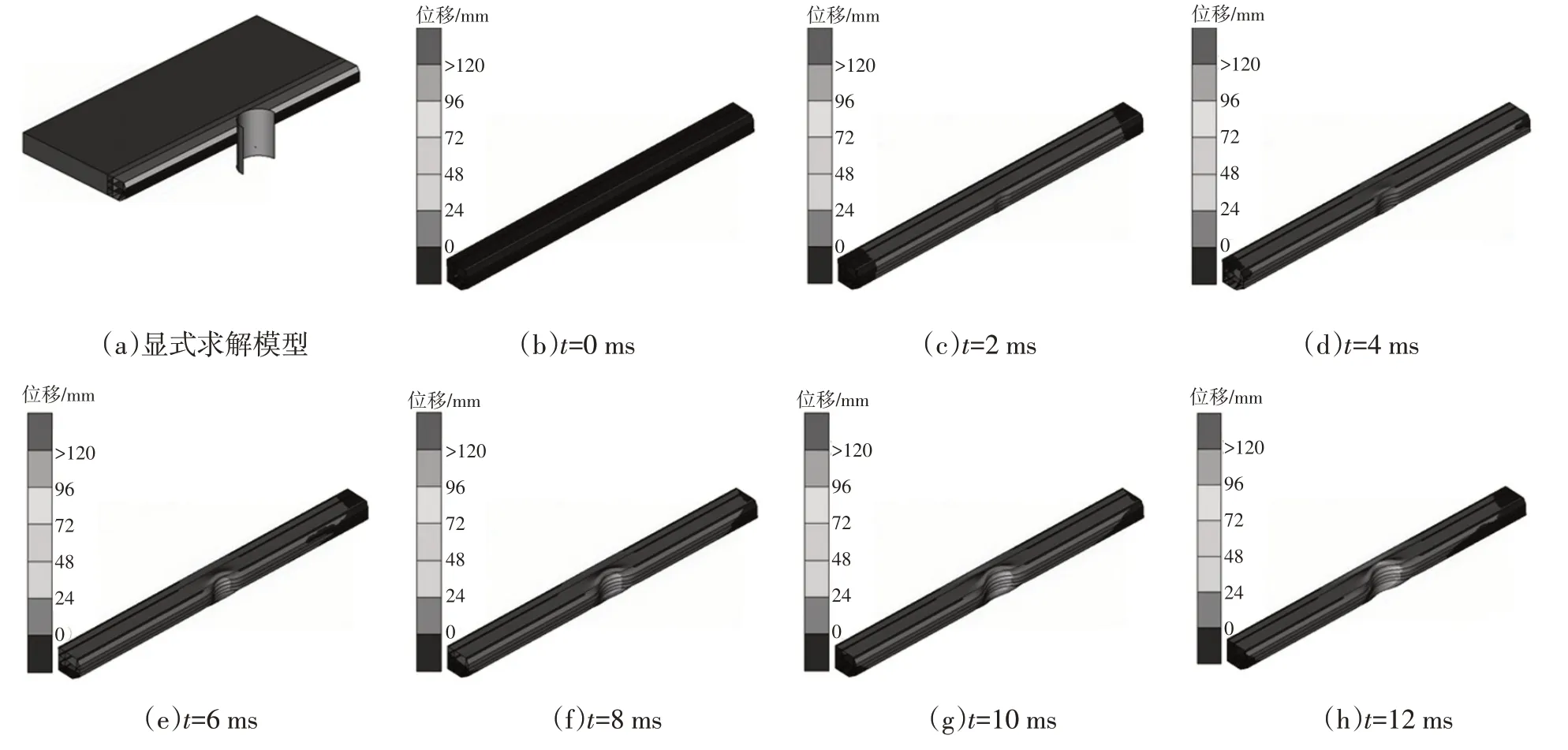
图1 动力学计算过程位移场变化示意

等效静载荷法不同时刻响应示意如图2 所示，通过将显式计算过程中特定时刻CAE 模型节点位移场与静力学CAE 模型刚度矩阵相结合，换算得到静力学CAE 模型各节点等效静载荷，进行等效静载荷工况构建，如式（1）所示。

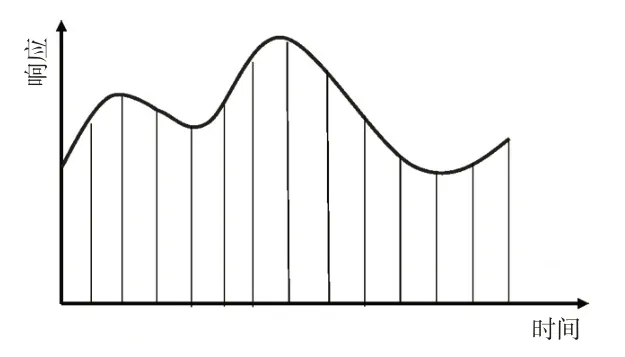
图2 等效静载荷法不同时刻响应示意

式中：fESL(ti)为ti时刻等效静载荷工况的等效静载荷，KL为等效静载荷工况的刚度矩阵，ZN(ti)为ti时刻显示计算过程中的节点位移场。

将等效静载荷工况与梯度法优化技术相结合，采用图3 所示的优化流程，实现对大变形非线性载荷下零部件结构的拓扑优化、尺寸优化、拓扑尺寸优化、形貌优化、形状优化等优化设计。

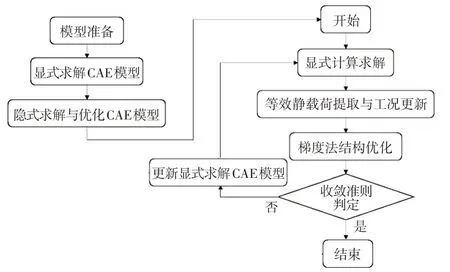
图3 基于等效静载荷法的非线性结构优化流程

2.2 ESLDYNA软件

Omniquest 公司的Genesis 软件是一款集静力学分析和梯度法优化技术为一体的CAE 分析与优化软件，自带的Genesis 求解器完美兼容Nastran 关键字，具备结构拓扑优化、拓扑尺寸优化、尺寸优化、形貌优化、形状优化、自由形状优化、复合材料优化、增材制造3D 打印和晶格微结构优化等功能。公司软件团队在Genesis 结构优化软件基础上，基于等效静载荷法开发了非线性结构优化工具ESLDYNA，支持碰撞工况下非线性结构优化需求。该工具可直接解析LS-DYNA 求解器的计算结果文件d3plot 或nodout，提取模型中各零件单元节点在特定变形时刻的位移场，根据Genesis 有限元模型刚度矩阵，反求各节点等效载荷，作为结构优化中非线性工况载荷定义，驱动碰撞工况下的零部件非线性结构优化设计。

ESLDYNA 软件与LSDYNA 求解器兼容性较好，支持碰撞安全模型中非拓扑设计域的材料卡加密要求，其位移场映射功能满足静力学和碰撞模型的网格标准差异化需求，降低工程师使用门槛[6]。ESLDYNA 软件自诞生以来，被广泛用于碰撞工况下的整车和零部件结构优化[6-8]。

除常规等效静载荷法外，新发布的Genesis 2024版本中，增加了增量等效静载荷法（Incremental Equivalent Static Load，IESL）功能，如式（2）所示，通过对静力学CAE模型刚度矩阵和位移场的修正，更加真实地复现单元在碰撞工况中的受力状态，提高碰撞过程中零部件节点的等效载荷精度，更有利于大变形碰撞工况下的结构优化设计。

式中：fESL(ti)为ti时刻等效静载荷工况的等效静载荷，KL(ti-1)为ti时刻等效静载荷工况的修正刚度矩阵，ΔZN(ti)为ti时刻等效静载荷工况的修正位移场，ZN(ti)和ZN(ti-1)分别为显示计算过程中ti时刻和ti-1时刻的位移场。

3 CAE模型搭建与优化问题定义

3.1 有限元建模与工况定义

本研究案例来源于某车型电池包和门槛梁集成方案，根据C-NCAP 管理规则（2021 年版）[1]，搭建侧面柱撞CAE 模型。模型中挤压铝腔体设计域采用六面体/五面体单元填充，挤压铝外轮廓采用2 mm 厚的壳单元模拟，与设计域共节点连接。在通用前处理软件中，将LS-DYNA 碰撞模型转换为Nastran 格式的静力学CAE 模型，初始模型共计网格数量约18 万个，如图4 所示。

图4 侧面柱撞简化模型

3.2 挤压铝截面侧面柱碰拓扑优化

分别采用线性拓扑优化技术和基于等效静载荷法的非线性拓扑优化技术对挤压铝门槛梁设计域进行传力路径优化。线性拓扑优化过程中，静力学加载工况定义如图5 所示，约束远离撞击侧电池包截面的全部自由度，在柱子中心点施加沿碰撞方向800 kN 的简化载荷，进行加载。

图5 线性拓扑优化模型工况加载示意

梯度法拓扑优化技术无法直接以碰撞工况的吸能指标进行优化，需进行性能等效。通常情况下，材料牌号相同时，结构的刚度与吸能效率和材料利用率正相关，基于此假设，线性拓扑优化问题可定义为一定质量分数约束下的刚度最大化或应变能最小化问题，如式（3）所示：

式中：E为静力学工况下的CAE 模型应变能，Mf为设计域质量分数。

采用等效静载荷法非线性拓扑优化技术时，为使结构在整个变形空间内均具有较高的刚度和吸能效率，需确保碰撞工况中设计域在加载方向变形充分。本案例中碰撞模型采用刚性柱沿碰撞方向的强制位移法进行加载，d3plot 输出间隔定义为2 ms。为了确保优化方案能充分兼顾碰撞过程中不同变形时刻的结构效率，等效静载荷工况采用与d3plot 相同的时间间隔进行定义，如表1 所示。

表1 等效静载荷工况列表 ms

非线性拓扑优化问题定义采用与线性拓扑优化相同的假设，以表1 中的10 个等效静载荷工况应变能之和最小作为优化目标，设计域质量分数上限作为约束，如式（4）所示。

式中：Ei为等效静载荷工况模型应变能，Mf为设计域质量分数。

线性拓扑优化与非线性拓扑优化结果如图6所示。根据结果可知，线性拓扑优化中，结构变形和受力集中在撞击侧，致使优化方案中靠近碰撞侧的材料保留较多，远离碰撞侧的材料保留较少；非线性拓扑优化方案中，优化目标中同时考虑了不同变形时刻的结构刚度，优化方案材料分布相对均匀。侧面柱碰撞工况下门槛梁结构合理的刚度分布通常表现为靠近撞击侧较小，远离撞击侧较大，以此来确保结构变形次序的稳定性，优化结果显示，相对于线性拓扑方案，基于等效静载荷法的非线性拓扑优化方案更符合侧面柱碰撞工况中门槛梁刚度设计策略。

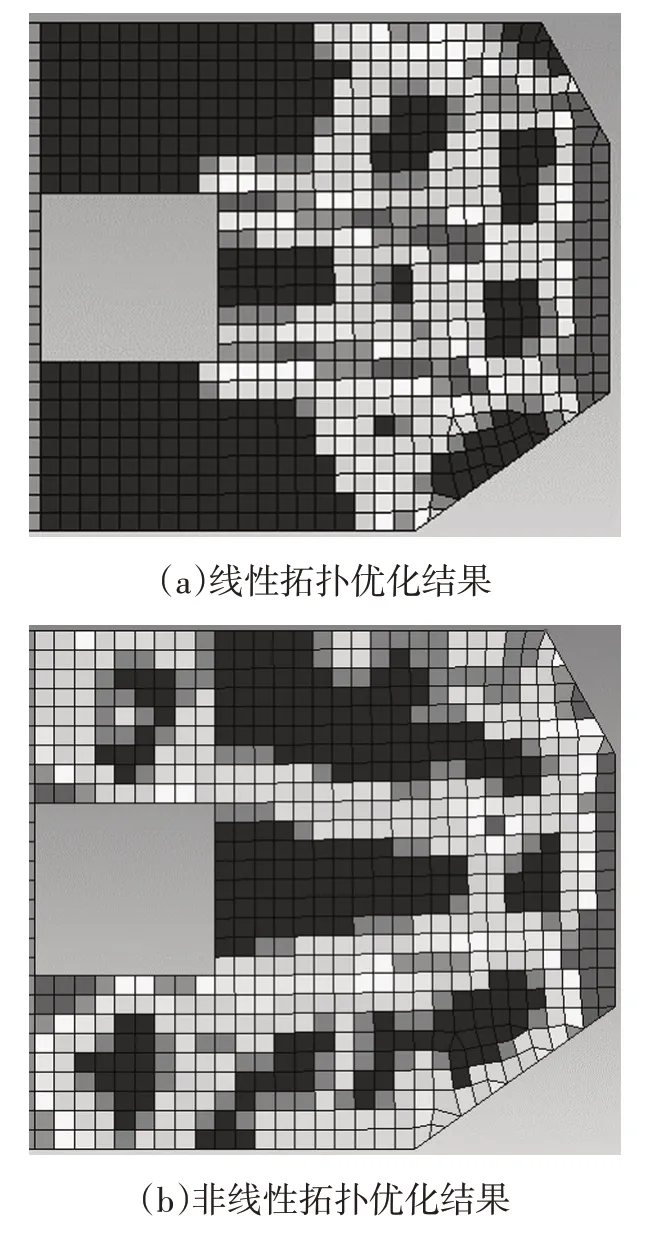
图6 拓扑优化结果对比

3.3 挤压铝门槛粱侧面柱碰工况料厚优化

基于非线性拓扑优化结果，对加强筋方案进行重构，得到初始门槛梁截面方案形式，如图7a 所示。本案例中，门槛梁和电池包总成在碰撞过程中，需在65.5 kJ 的碰撞能量下，确保门槛梁前端面Y向侵入量小于116 mm，以减少车体侵入；后端面Y向侵入量小于40 mm，以规避门槛粱对电池模组的挤压，因此在给定的门槛梁截面形式下，需对各筋料厚进行优化设计，获取满足设计约束的轻量化厚度分布方案。

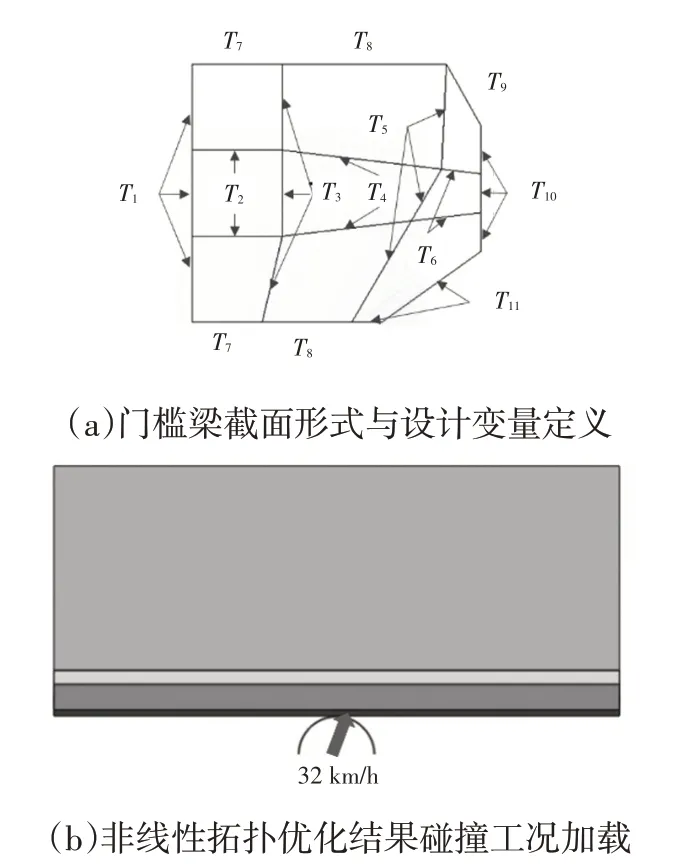
图7 料厚优化用碰撞模型

门槛梁料厚优化问题定义如式（5）所示：

式中：M为门槛梁质量，Ti为门槛梁各筋料厚，df和dr分别为门槛梁前端面和后端面最大变形时刻的Y向侵入量。

门槛梁设计变量定义、碰撞工况加载如图7 所示。碰撞模型中，采用与非线性拓扑优化相同的约束形式，加载调整为配重状态下的刚性柱沿碰撞方向以32 km/h 的初速度撞击简化模型。

由于线性梯度法优化技术在碰撞工况中无法直接使用，国内外学者常采用基于近似模型的数值优化方法[9-10]开展碰撞工况下的零件料厚优化。当设计变量较多（＞10）时，数值优化技术需要消耗大量的硬件资源生成足够数量的DOE 样本来提升近似模型精度，这使其在大变量优化问题中使用受限，工程应用普及率低。基于等效静载荷法的梯度法优化技术，弥补了传统线性梯度法优化技术的缺点，可以用于碰撞工况下的零部件料厚优化。为了对比不同优化方法的优化效果，分别采用基于Kriging 近似模型和均匀拉丁方DOE 方法的数值优化技术、传统等效静载荷法和增量等效静载荷法的梯度法料厚优化技术，对式（5）中的优化问题进行求解，结果如表2 所示。

表2 优化结果对比

根据表2 可知，数值优化方法受限于近似模型函数形状和精度，在满足侵入量约束的前提下，优化方案轻量化效果较差；传统等效静载荷法的梯度法料厚优化过程中，碰撞工况位移场为特定时刻绝对值，采用式（5）优化问题定义时，仅需定义最后若干时刻的等效静载荷工况，无法兼顾碰撞过程中的模型变形影响，优化方案相对于数值优化结果有2.1 kg 的优势；增量等效静载荷法的梯度法料厚优化过程中，采用等效静载荷工况位移叠加的方式定义约束节点侵入量，约束响应灵敏度计算过程中可兼顾各变形时刻的零件变形状态，优化方案的轻量化效果较好，且挤压铝门槛梁前后端面最大侵入量相比较基于近似模型的数值优化方法和传统等效静载荷的梯度法料厚优化方法更小。

除此之外，为了对比3 种优化技术的硬件资源消耗和优化效率，数值优化中的DOE 样本计算和等效静载荷法优化求解，采用相同的硬件资源配置。统计结果显示，数值优化过程中，在不考虑优化求解过程时，仅234 个DOE 样本的计算时间耗时已达到2 h 17 min，而传统等效静载荷法和增量等效静载荷法的梯度法料厚优化过程的完整求解时间分别为28 min 和1 h 29 min，均优于数值优化技术。由此可知，基于等效静载荷梯度法料厚优化技术在资源消耗和优化效率方面要远优于基于近似模型的数值优化技术。

4 结束语

基于等效静载荷法的梯度法优化技术，以某乘用车简化电池包门槛梁系统为例，探索了挤压铝门槛梁结构的正向设计方法。结果表明，概念设计阶段，相比较传统的线性拓扑优化技术，基于等效静载荷法的非线性拓扑优化技术可以得到更加符合安全变形策略的门槛梁截面路径；详细设计阶段，相比较传统的数值优化技术，基于等效静载荷法的梯度法料厚优化技术，优化效果和效率更佳；且相对于传统的等效静载荷法，增量等效静载荷法可以在相同的约束条件下得到更为合理的料厚分配方案，最大化挤压铝门槛梁结构设计的轻量化效果。