表面织构对高速插针机构导轨的表面摩擦性能影响

王星龙, 陶宗杰, 杨泊莘, 安 琦

(1.华东理工大学 机械与动力工程学院,上海 200237;2.泰科电子(上海)有限公司,上海 200030)

插针机构功能是指插针快速插入印制电路板孔洞,实现两者的紧密电气连接。插针机构中的导轨是其核心部件,导轨中滑块在工作过程中长时间高频往复运动,其摩擦面磨损较快。如何采取措施有效改进其润滑性能、降低磨损十分必要。

关于导轨润滑方面有不少专家学者进行了研究。于如飞等[1]从理论与试验出发对表面织构化技术研究进行了综述。张赟等[2]利用激光加工技术在导轨摩擦副上加工出了4种不同微织构,研究了微织构形状对导轨副摩擦性能的影响。Dinesh Babu等[3]对钛合金表面进行织构化处理,分析了其磨损性能。Zhang等[4]采用激光在钢导轨摩擦副上制造仿生六边形微纹理,研究了不同微织构分布和方向、载荷和滑动速度对导轨摩擦性能的影响。Yue等[5]研究了边界润滑下表面织构对滑动导轨摩擦学性能的影响。Gachot等[6]讨论了表面纹理对Stribeck曲线的影响以及保形和非保形接触之间的区别。韩洪松等[7]利用激光微织构技术在45号钢盘试样端面分别加工规则及有序排列的微凹坑和微凸起。张东亚等[8]仿真研究了沟槽织构表面的流体动力效应。Niu等[9]在中碳钢的表面上制造凹坑纹理表面,通过试验发现凹坑深度是影响摩擦磨损性能的主要因素。Rodrigues等[10]研究了电化学织构产生的不同形貌对润滑状态的影响及其对织构表面耐磨性的影响。Cheng等[11]采用混合弹流润滑模型研究线接触织构表面的摩擦磨损,得到有利于提高表面摩擦学性能的最优织构形式。Pawlus等[12]研究了压痕形状和面积密度对磨料磨损的影响,通过试验得出球形凹坑优于水滴形凹坑。Wan等[13]分析了固体润滑对微织构表面的润滑机理,以及微织构尺寸对摩擦系数的影响。Zhang等[14]研究了不锈钢纹理表面的摩擦学特性,发现表面纹理的有效性在很大程度上取决于纹理的深度和几何形状。

通过上述文献可知,在导轨表面加工出表面织构可以实现其润滑性能的改进。但目前针对表面织构摩擦副的研究多为在单一速度、固定载荷下进行分析,这些研究大多不考虑油膜挤压和表面粗糙度对油膜压力的影响,同时专门针对高速插针机构中导轨这一特殊应用场景下的研究较少,将表面织构引入插针机构的导轨摩擦副很有意义。为此本文以插针机中导轨摩擦副为研究对象,将表面织构引入到摩擦副表面,考虑表面粗糙度、载荷波动、速度变化、时变油膜挤压效应等因素,分析表面织构对其摩擦性能的影响,将Greenwood和Tipp建立的粗糙度接触模型以及Patir和Cheng修正后的平均油膜流体润滑模型耦合,构建混合摩擦模型,应用MATLAB分析有关参数的影响。

1 具有表面织构导轨混合摩擦模型

1.1 表面织构的引入方法

如图1(a)所示,插针机构中导轨由底座、滑块和两块挡板组成。为了降低导轨摩擦面的摩擦,将表面织构引入到导轨摩擦副,在导轨的底座表面开设激光微观点阵,如图1(b)所示,本文将实际加工的表面织构近似看作球状凹坑。

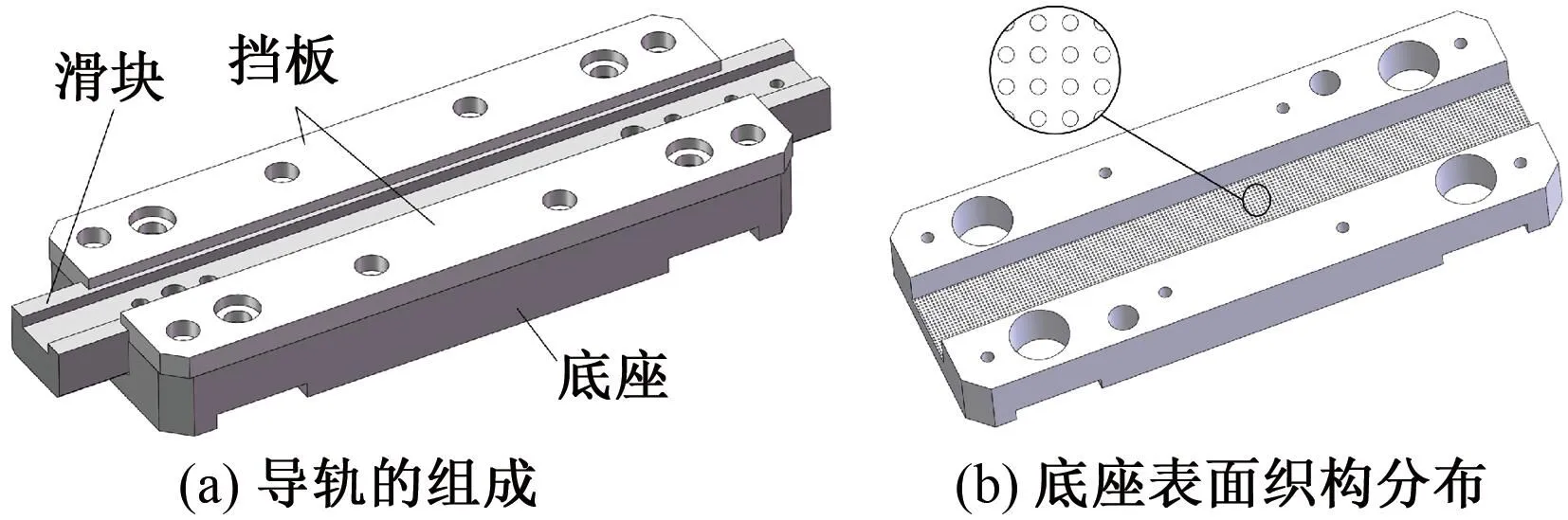
图1 底座的表面织构Figure 1 Surface texture of the base

图2所示为表面织构分布图,具有表面织构的底座摩擦面总长为L、总宽为W。长度和宽度方向分别设有NL和NW个织构单元。每个单元的正中间设有球状凹坑,凹坑的深度为hp、半径为rd,初始油膜厚度为c、滑动速度为U、单个织构单元的长度l、宽度w。织构面积占有比Sp为

(1)

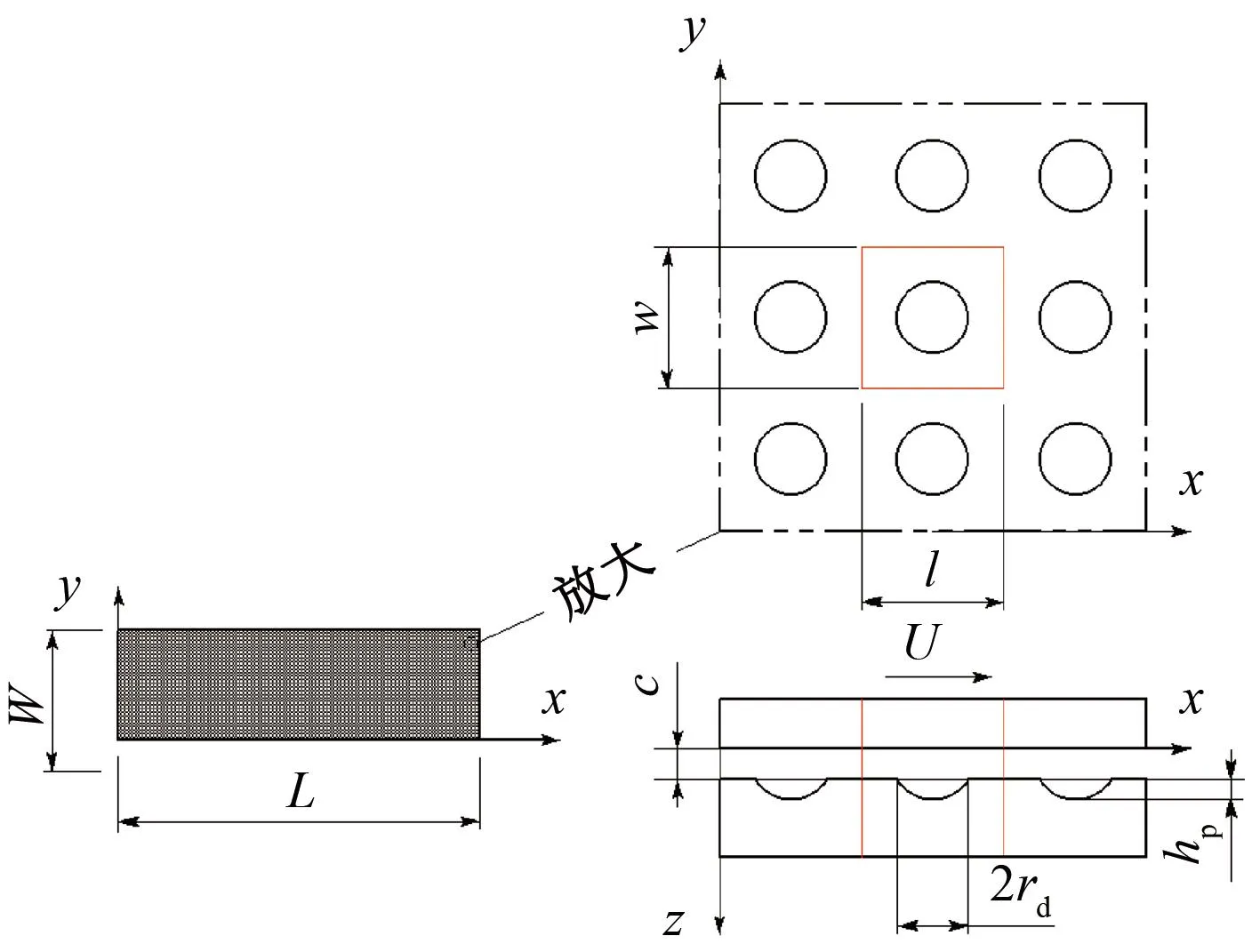
图2 表面织构分布图Figure 2 Surface texture distribution

图3 油膜厚度示意图Figure 3 Oil film thickness diagram

由图3可知,名义油膜厚度h计算公式为

(2)

式中：d为(x,y)到织构中心(x0,y0)的距离;Ω为以半径为rd的凹坑区域。如图3所示,hT为实际油膜厚度,其大小为h+δ1+δ2。δ1、δ2分别为底座和滑块表面随机粗糙度高度,分别服从以0为均值,σ1、σ2为偏差的正态分布,hT与h的关系为

(3)

式中：φc为接触因子。

基于AR模型的二维数字滤波技术,对导轨摩擦副粗糙表面进行计算机模拟,生成具有指数形式的粗糙表面。其自相关函数为

(4)

式中：βx、βy分别为x、y方向上的相关长度。

1.2 平均油膜流体润滑模型

为分析摩擦副的润滑特性,应用Patir和Cheng修正后的平均雷诺方程为

(5)

1.3 粗糙度接触模型

采用Greenwood和Tipp建立的粗糙度接触模型求解粗糙表面微凸体间的接触力为

(6)

式中：WA为粗糙表面微凸体接触力;λ、β分别为微凸体密度和曲率半径;E′为两表面综合弹性模量;F5/2(H)表达式为

1.4 载荷平衡方程

导轨的滑块与底座摩擦副承受的载荷为自重,其平衡方程为

(7)

式中：pe为纵向外载荷;ξ(0,30)为以0为均值、30为方差的正态分布随机数;M2为滑块质量;pG为自重在摩擦面产生的压力。

油膜承载力Wp与Ape、WA关系为

(8)

油膜承载力Wp为

(9)

式中：m、n分别为长度和宽度方向细分份数;i、j、k分别为差分格式的二维雷诺方程在x、y、τ方向的网格编号。

2 模型的数值求解方法

2.1 雷诺方程的变量无量纲化

在数值求解之前,引入雷诺边界条件,并对雷诺方程各物理量进行无量纲化：

(10)

将式(10)代入雷诺方程得

(11)

2.2 雷诺方程的离散化

应用五点差分格式离散化二维雷诺方程,将离散后的各项代入雷诺方程：

(12)

2.3 求解步骤

假设插针机构的运动周期为T,将一个动作周期T均分为q个时间间隔,每个时间间隔的Δt=T/q。MATLAB程序计算流程如图4所示。具体步骤如下。

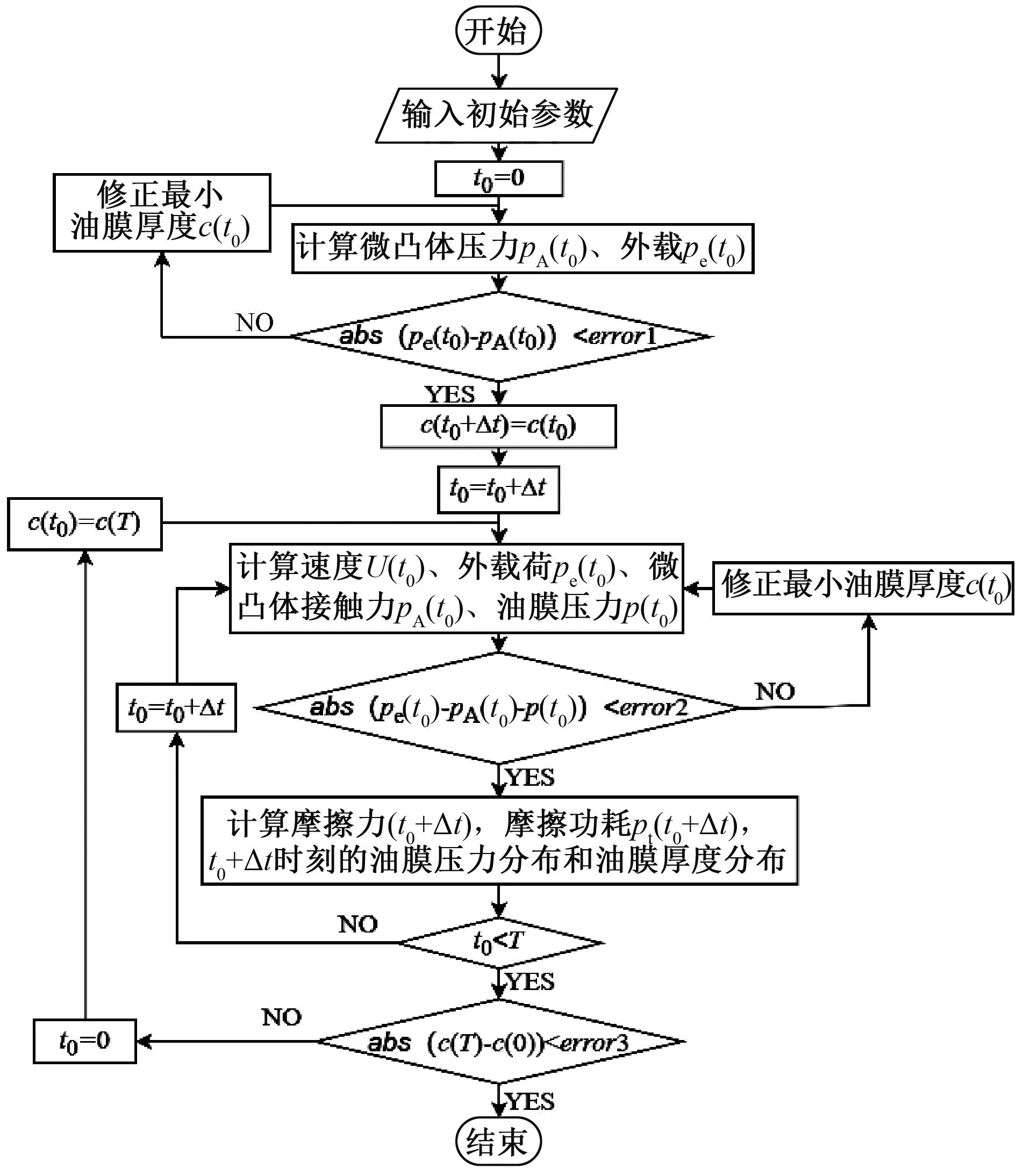
图4 主程序计算流程图Figure 4 Calculation flow chart

步骤1 求得t0=0时不考虑载荷变化和速度变化时的油膜厚度c(t0),设t0时刻微凸体接触力pA与外载荷pe相等。

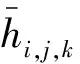
当一个周期结束后,油膜厚度、油膜压力、摩擦功耗将与初始时刻应当相等。因此检验t=0时刻与t=T的油膜厚度是否相等,如果不相等,将t=T时刻的油膜厚度c(T)作为c(0)继续依次进行步骤1～3,直到t=0时刻与t=T的油膜厚度相等。

3 算例分析

3.1 参数确定

本模型的相关参数如表1所示。

表1 相关参数Table 1 Correlation parameters

3.2 摩擦副表面微观形貌计算机模拟

如图5所示,以σ1=1.2 μm对摩擦副表面进行计算机模拟。可以看出3×3单元底座摩擦表面存在球状凹坑,与实际底座表面较为符合。

3.3 模型的对比验证

将文献[15]中针对光滑圆柱状织构表面的模型中的输入参数和压力无量纲化参数导入本文模型,求解出的无量纲油膜压力分布如图6(a)所示。相比文献[15]得出的图6(b)所示结果,本文模型油膜压力分布相似性大,压力值略微偏高,这是由于本文模型考虑了粗糙度对油膜压力的影响。

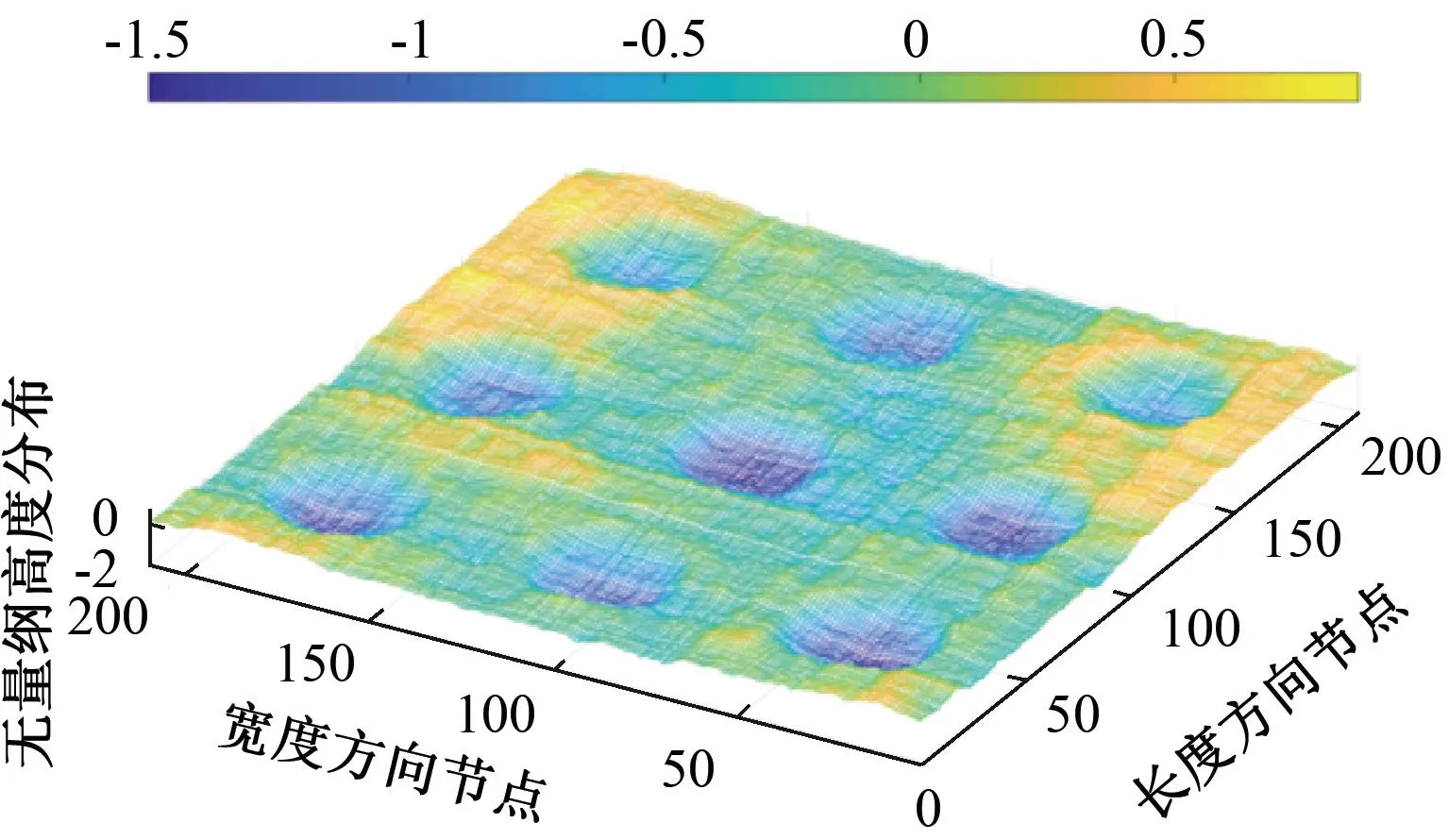
图5 底座表面的微观形貌Figure 5 Microstructure of the base surface

图6 油膜压力对比Figure 6 Comparison of oil film pressure

3.4 单元数量对油膜压力分布的影响

如图7所示,设rd=30 μm、Sp=30%、hp=3 μm、U=2 m/s、σ1=0.9 μm、c=6 μm、pe=3 333 Pa,NL和NW取3～13,分析其稳态油膜压力。可以看出,在其他条件一定的情况下,随着长度与宽度方向的织构单元数量增加,摩擦副最外层以内的单元压力分布保持恒定,故确立NL=3、NW=3摩擦副的最中间单元作为油膜承载力的计算依据。

图7 单元数对油膜压力分布的影响Figure 7 Influence of the number of elements on the pressure distribution of oil film

3.5 混合润滑各关键时间点的油膜压力分布

如图8所示,选取rd=55 μm、Sp=30%、hp=3 μm、σ1=1.2 μm分析油膜压力分布随时间变化。可以看出,油膜厚度变化略微滞后于速度变化,这是由于挤压效应的存在,导致油膜不需要迅速变化就能立即产生动压效应来响应速度的变化。

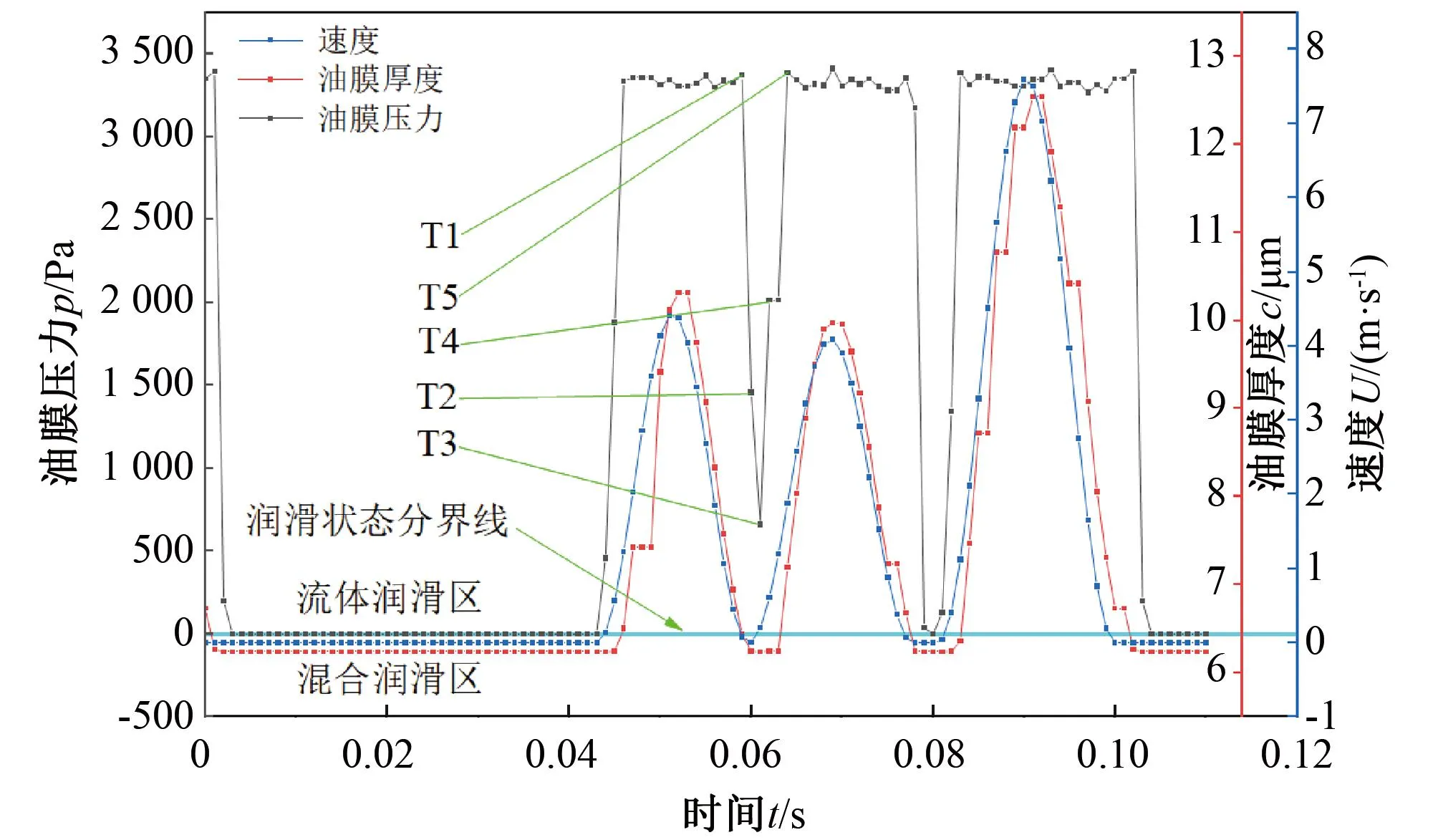
图8 摩擦副的速度、油膜厚度、油膜压力变化Figure 8 Velocity, oil film thickness and oil film pressure changes of friction pairs

如图9所示为T1～T5共5个关键时刻的瞬时油膜压力分布。在T1时刻由于摩擦副速度较大,摩擦副处于完全流体润滑阶段,油膜压力主要由动压效应和表面粗糙效应产生;该时刻以后由于速度降低,油膜压力随之下降,挤压效应作用逐渐突出,动压效应和表面粗糙效应作用逐渐削弱;到了T3时刻速度降为0,动压效应与表面粗糙效应完全消失,挤压效应作用最为突出;T3以后由于速度从0逐渐增大,油膜压力和油膜厚度随之增大,动压效应与表面粗糙效应逐渐恢复,挤压效应逐渐削弱;到了T5时刻摩擦副再次进入完全流体润滑阶段。

3.6 表面粗糙度对具有织构摩擦副润滑特性的影响

如图10所示,以rd=30 μm、Sp=30%、hp=3 μm分析表面粗糙度对具有表面织构摩擦副的影响。可以看出,随着表面粗糙度的增大,混合润滑阶段的油膜压力降低、微凸体压力升高,当粗糙度方差σ1从1.0 μm升高1.6 μm时,油膜压力的最大降低幅度为58%。

3.7 织构尺寸参数对摩擦副润滑特性的影响

3.7.1 微型凹坑半径rd的影响

如图11所示,以Sp=30%、hp=3 μm、σ1=1.2 μm分析微型凹坑半径rd对具有表面织构摩擦副的影响。可以看出,随着微型凹坑半径rd的增大,混合润滑阶段的油膜压力随之增大,当微型凹坑半径rd从30 μm升高60 μm时,油膜压力的最大升高幅度为156%。

图9 摩擦副关键时间节点的油膜压力Figure 9 Oil film pressure at critical time node of friction pair

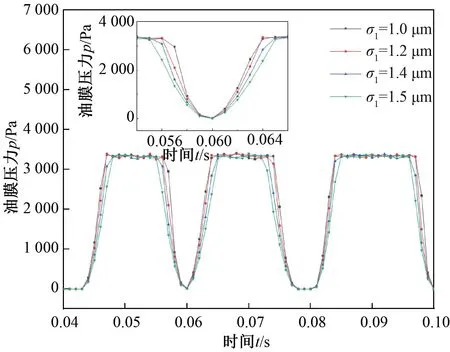
图10 粗糙度对具有织构摩擦副油膜压力的影响Figure 10 Effect of roughness on film pressure of textured friction pairs

3.7.2 面积占有比Sp的影响

如图12所示,以rd=40 μm、hp=3 μm、σ1=1.2 μm分析表面织构的面积占有比Sp对具有表面织构摩擦副的影响。可以看出,随着面积占有比Sp的增大,混合润滑阶段的油膜压力先增大后减小,当Sp=40%取得最大的油膜压力。

3.7.3 表面织构尺寸hp的影响

如图13所示,以rd=30 μm、Sp=40%、σ1=1.2 μm分析微型凹坑深度hp对具有表面织构摩擦副的影响。可以看出,随着微型凹坑深度hp的增大,混合润滑阶段的油膜压力先增大后减小,当hp=5 μm时取得最大的油膜压力。

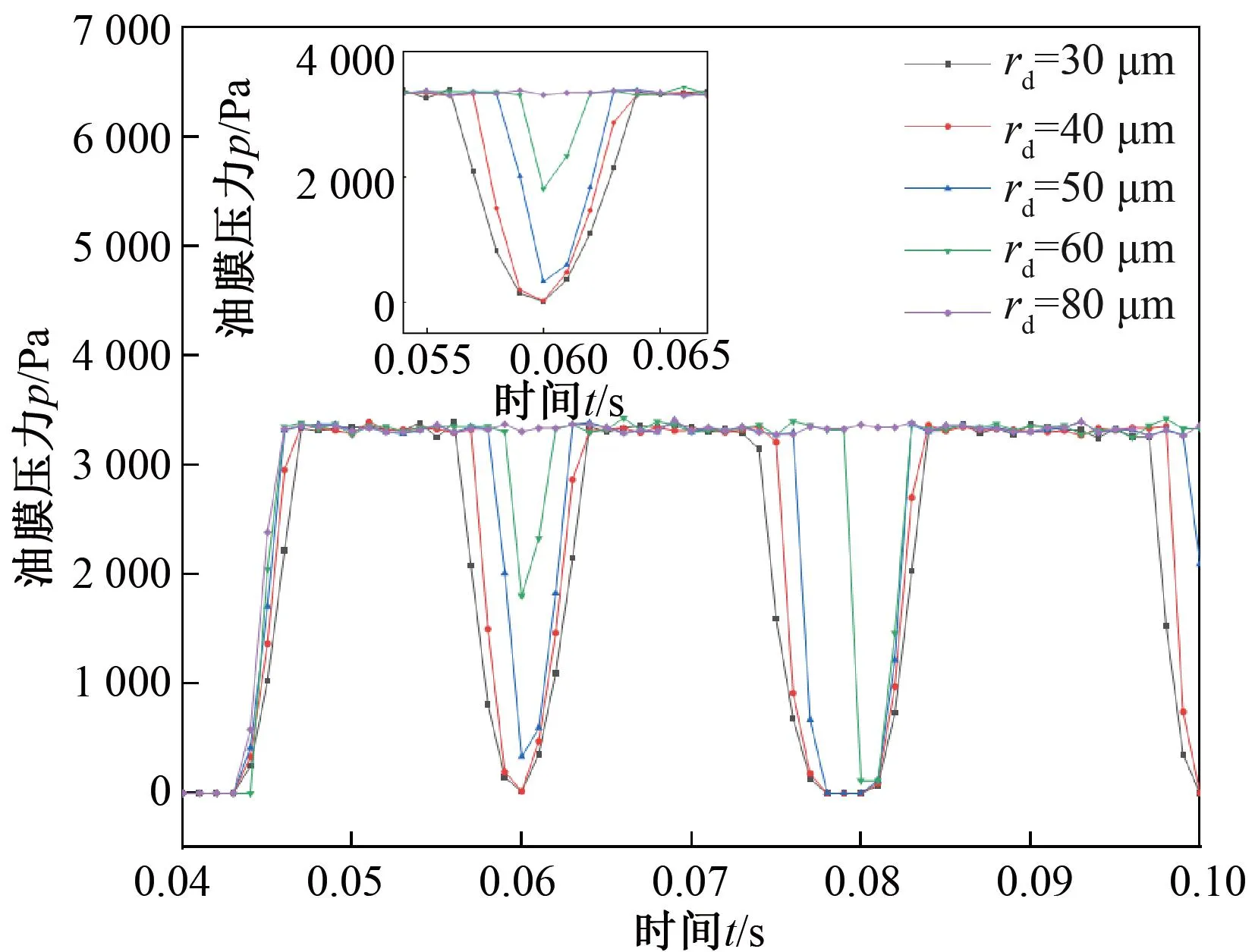
图11 rd对具有织构摩擦副油膜压力的影响Figure 11 Effect of rd on oil film pressure with textured friction pairs

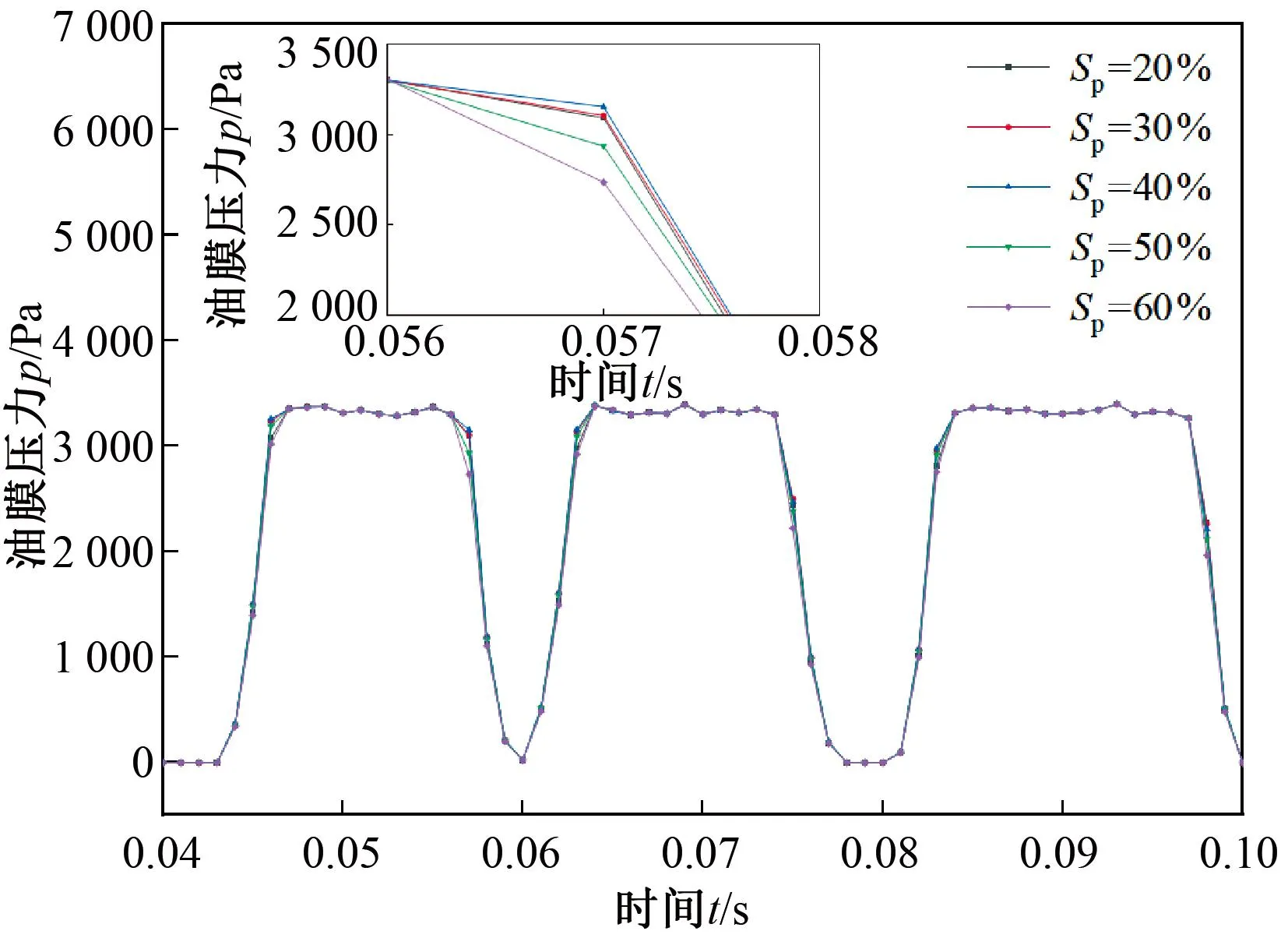
图12 SP对具有织构摩擦副油膜压力的影响Figure 12 Effect of Sp on the pressure of oil film with textured friction pairs

图13 hp对具有织构摩擦副油膜压力的影响Figure 13 Effect of hp on the pressure of oil film with textured friction pairs

4 结论

(1)以插针机构中导轨摩擦副为研究对象,考虑表面粗糙度、载荷波动、速度变化、时变油膜挤压效应等因素,分析表面织构对其摩擦性能的影响。应用计算机模拟生成粗糙表面,将粗糙度接触模型和修正后的平均油膜流体润滑模型耦合构建混合摩擦模型,通过数值方法计算出油膜压力、微凸体压力、油膜厚度。

(2)分析了混合润滑阶段摩擦副的油膜压力变化规律,发现由完全流体润滑状态转变到混合润滑状态过程中,动压效应与表面粗糙效应作用逐渐减弱,油膜挤压效应作用逐渐增强;由混合润滑状态转变到完全油膜润滑状态过程时结论相反。

(3)分析了表面粗糙度和织构尺寸对摩擦副润滑特性的影响,发现随着表面粗糙度的增大,润滑性能变差;随着微型凹坑半径rd的增大,润滑性能提升;随着织构的面积占有比Sp的增大,润滑性能先提升后变差;随着微型凹坑深度hp的增大,润滑性能先提升后变差;当Sp=40%、hp=5 μm时获得最优润滑性能。