富水地层深基坑施工诱发邻近建筑物变形分析: 以济南地铁R2线烈士陵园站深基坑为例

刘贵香, 刘毅, 冯新绪, 王勇, 马少坤, 张加兵*

(1.中铁北京工程局集团有限公司, 北京 100097; 2.济南轨道交通集团有限公司, 济南 250014; 3.广西大学土木建筑工程学院, 南宁 530004)

随着中国城市现代化轨道交通的快速发展,地铁车站基坑工程面临着开挖深度越来越大、周边环境越来越复杂等问题。深基坑工程施工不可避免地会引起地表沉降,当影响范围内存在建筑物时,可能导致其结构倾斜、开裂,甚至倒塌等,严重危及既有建筑物正常使用[1-2]。因此,在深基坑开挖过程中如何减小对邻近建筑物及周边环境的影响,是城市轨道交通建设的重中之重。

在深基坑施工过程中通常将坑外地表沉降作为邻近建筑物沉降,Moormannn[3]基于大量监测数据,提出根据围护结构位移预测坑外地表沉降的方法。杨敏等[4]采用数值模拟方法,得到坑外地表沉降曲线呈正态分布规律。但上述方法均未考虑坑外建筑物基础刚度能有效抵抗土体变形,导致计算结果大于实测值。范凡等[5]、章红兵等[6]认为,建筑物沉降主要来源于基础下方软卧土层的变形,并提出一种基坑施工诱发邻近建筑物沉降的计算方法。后来研究发现基坑施工诱发邻近建筑物变形不仅受土体开挖卸载影响,还与建筑物自身结构和地下水渗流等因素密切相关。Zhang等[7]研究认为,在基坑开挖过程中,地层沉降不仅受土体开挖影响,支护桩间渗水也会引起土体流失,从而造成地层损失,导致临近建筑物沉降增加。Li等[8]通过现场监测结果发现基坑开挖造成坑外两侧土体横向应力释放,会导致建筑物承重墙产生拱形变形。刘念武等[9]通过现场监测结果发现建筑物基底压力与变形之间存在关联,基坑附近楼层较高的建筑物沉降与地表土体沉降变化相差较大,而楼层较低则与地表土体沉降接近。Zheng等[10]分析了地下水回灌时基坑排水导致坑外地下水位深度变化和地表沉降规律,并提出地下水回灌措施能够有效控制邻近建筑物变形。目前,同时考虑降水、开挖、渗流和止水帷幕阻力等多因素作用下基坑施工引起周边建筑物变形规律仍比较少见。

鉴于此,依托济南轨道交通R2线烈士陵园站深基坑工程,采用现场监控量测手段对深基坑施工诱发邻近建筑物变形进行分析。再采用三维数值计算与现场监测数据相互印证,分析深基坑施工对邻近建筑物变形的影响,并探讨不同钢支撑间距、止水帷幕深度对邻近建筑物变形的影响,以期为类似富水地层深基坑邻近建筑物施工提供参考。

1 工程背景

1.1 工程概况

济南轨道交通烈士陵园站位于规划飞跃大道与凤凰路交叉口,为R2线与M1线呈“L”型换乘车站。其中,R2线沿规划飞跃大道东西向布置,M1线沿规划凤凰路南北向布置,烈士陵园站平面布置如图1所示。R2线烈士陵园站为地下两层岛式车站,结构型式为钢筋混凝土箱型,站台宽度为14 m,有效站台长120 m。M1线烈士陵园站为地下三层岛式车站,结构型式为钢筋混凝土箱型,站台宽度为14 m,有效站台长140 m。车站周边建筑物密布,全部为条形浅基础框架结构楼房,A1～A2为济南市小企业创业辅导基地,A3～A8为济钢第三工业小区宿舍,其中与基坑最为接近的建筑物为转角区济钢工业小区第三宿舍A4,楼层高度为18 m,为六层混凝土钢筋结构楼房,与R2线基坑垂直距离为15.73 m,与M1线基坑垂直距离为42.22 m。

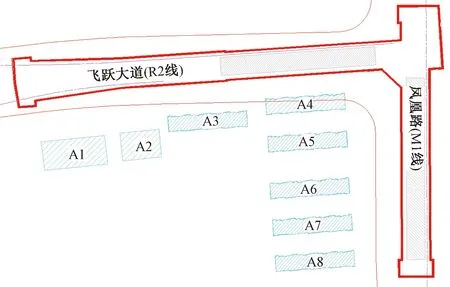
图1 烈士陵园站平面图Fig.1 Plan of martyr cemetery station

场地覆盖层主要由第四系全新统冲洪积～中上更新统坡洪积黏性土、碎石土组成,上覆新近人工填土,下伏燕山晚期闪长风化层和奥陶系石灰岩、大理岩。场地地下水位为地表以下10 m深,主要类型为第四系松散层孔隙潜水和岩浆岩裂隙水。考虑岩浆岩裂隙水和碳酸盐岩溶裂隙水具承压性,残积土分布区、裂隙发育带及局部风化深槽处施工时可能会发生地下水突涌情况。此外,场区内碎石层分布较多,地下水可相互连通,水力联系密切,因此需要设置止水帷幕来阻断坑内外地下水的联系。

1.2 依托工程监测及结果分析

根据文献[11]研究成果可知,建筑物到基坑的水平间距越近,其影响效应越大。因此,仅对距离基坑开挖三角区最近的建筑物A4进行分析,并对烈士陵园站基坑施工过程中围护桩体水平位移、建筑物沉降和地下水位等监测数据进行分析,监测点布置图如图2所示。

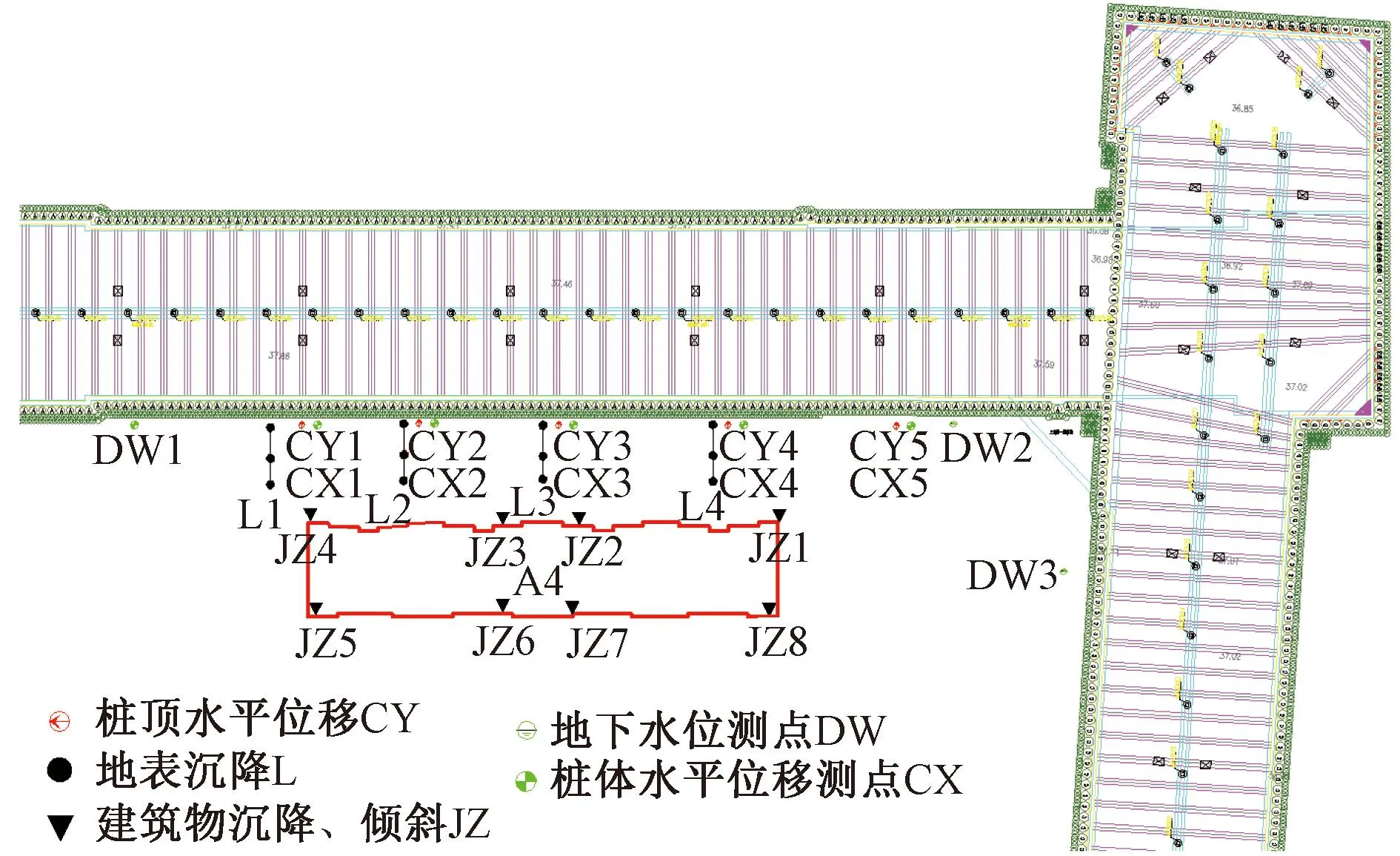
图2 建筑物A4邻近监测点平面布置图Fig.2 Layout plan of monitoring points adjacent to building A4

1.2.1 围护桩体水平位移分析

建筑物与基坑之间的围护桩体为主要监测对象,选取桩体水平位移监测点CX1～CX5进行研究,基坑完全开挖至底部时围护桩体水平位移随开挖深度的变化规律如图3所示。围护桩体水平位移呈“弓”形,即围护桩中间向坑内凸出,水平位移最大,上部向坑外产生较小水平位移,其下部基本不产生水平位移。监测点CX1～CX5最大水平位移不相同,其最大水平位移分别为22.0、21.8、4.8、3.0、2.5 mm,围护桩体CX1、CX2水平变形比CX3、CX4和CX5更大,这是由于基坑三角转角区采用了密集的钻孔灌注桩进行加固。另外,由于坑角效应[12],接近坑角处桩体水平位移会变得更小,因此桩体CX3、CX4和CX5相对其他测点的围护桩体水平位移更小。

图3 围护桩水平位移Fig.3 Horizontal displacement of retaining pile

1.2.2 建筑物变形分析

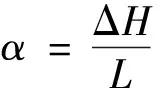
1.2.3 地下水位分析

选取DW1、DW2和DW3三个监测点的地下水位进行监测,三点都位于坑外,其地下水位最终变化量分别为+532、-231、+142 mm,如图4所示。可以看出,t=0时刻开始降水,地下水位不断下降,降水一段时间后,在t=15 h的时候在坑外进行回灌,坑外地下水位又开始回升,直到t=40 h之后水位开始趋于稳定。当渗流量与注入量保持平衡时,回灌水位就不再继续上升而稳定下来,此时在回灌井周围形成一个水位的上升锥,其形状与抽水的下降漏斗十分相似,只是方向正好相反。DW1和DW3监测点的地下水位最终不降反升,这是因为回灌井两侧的水头较高,而DW1、DW3与回灌井的距离较近,在回灌作用下水位反而上升。

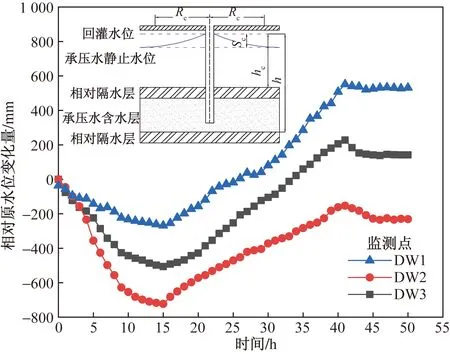
Rc为回灌影响半径;hc为回灌水位;Sc为水位升幅;h为地下水位图4 地下水位变化Fig.4 Changes in groundwater level

2 数值模拟

2.1 数值模型及材料参数

建立考虑地下水渗流的三维数值计算模型,模型取基坑开挖深度3～5倍范围,即模型长200 m,宽180 m,高50 m,基坑转角处存在六层高的建筑物,为天然条形浅基础框架结构,埋深2.0 m,尺寸61 m(长)×12 m(宽)×18 m(高)。为提高计算效率和准确模拟实际工况,对基坑区域的网格进行加密,整个模型共划分215 647个单元,156 065个节点,如图5所示。地层采用实体单元模拟,建筑物的条形基础、楼板和柱子均采用弹性实体单元。计算模型四周边界采用滚轴约束,下表面采用固定约束,上表面采用自由约束,初始应力场仅考虑自重应力。基坑的围护墙采用各向同性弹性模型,并在基坑围护墙两侧添加接触面,以便模拟土体和墙体之间的摩擦。建筑物材料参数如表1[13]所示。

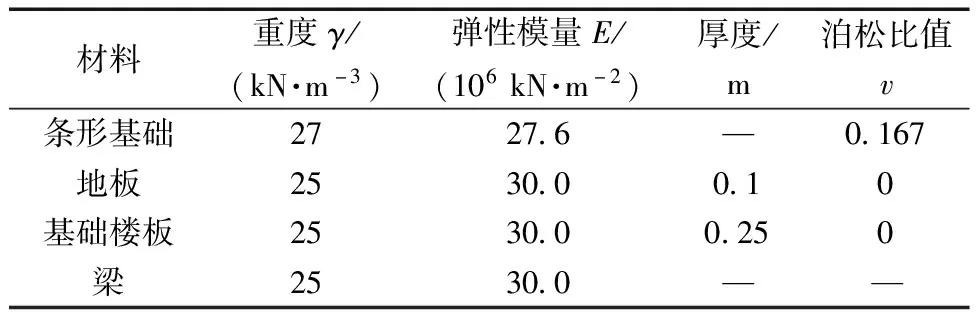
表1 建筑物材料参数[13]Table 1 Material parameters of buildings[13]

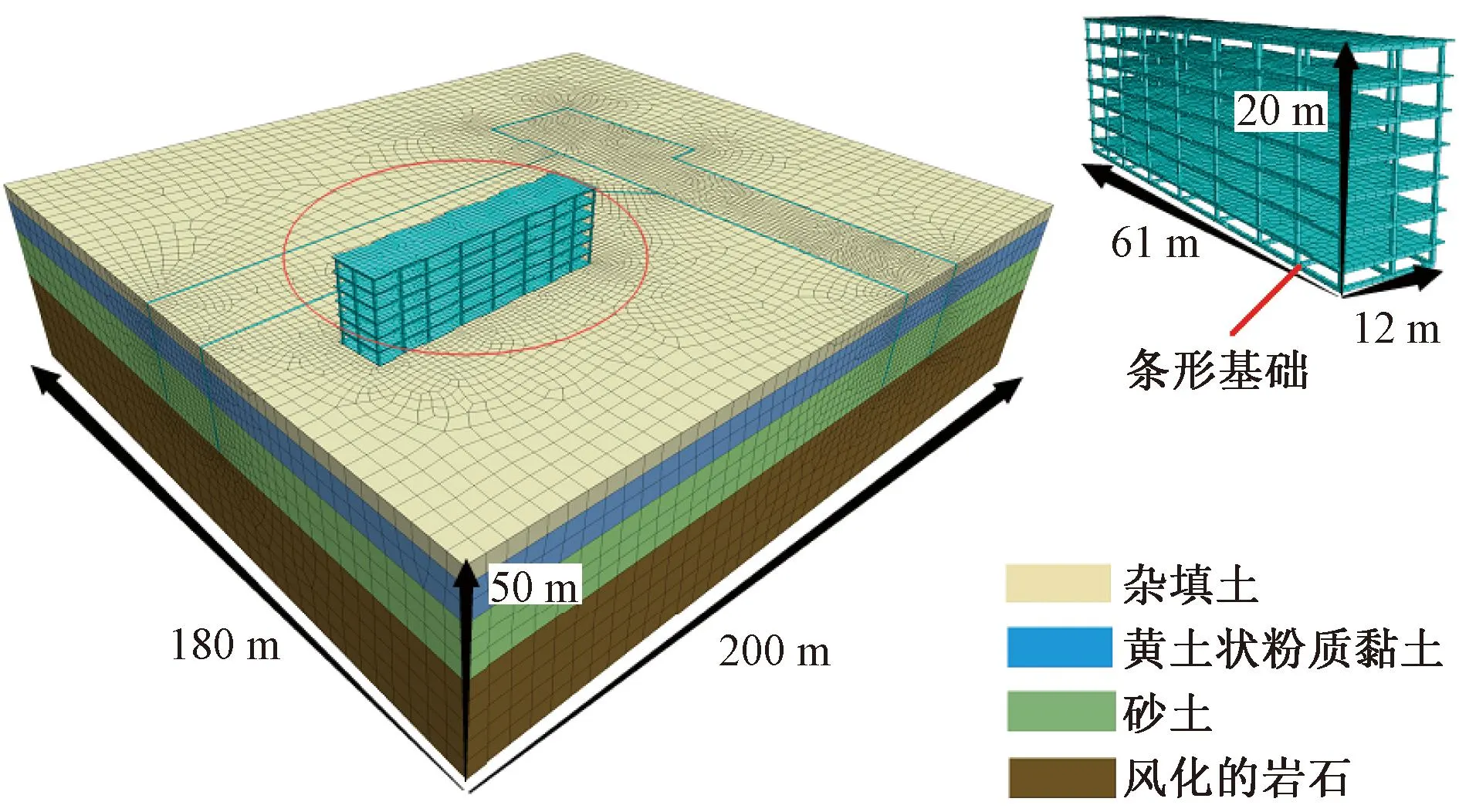
图5 基坑和建筑物模型Fig.5 Foundation pit and building models

2.2 本构模型

(1)

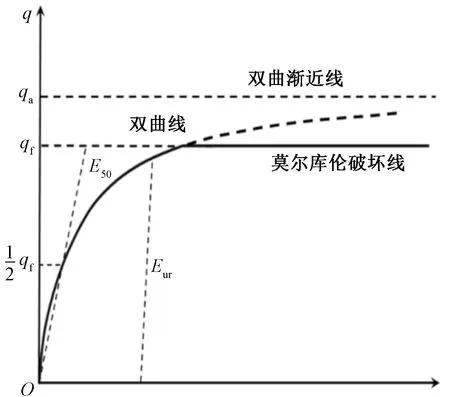
E50为割线刚度;Eur为卸载再加载刚度;qf为破坏应力;qa为渐近强度图6 剪切荷载下双曲线应力-应变关系Fig.6 Hyperbolic stress-strain relationships under shear loads

(2)

(3)

深基坑开挖时,MC模型由于土体卸载后坑底隆起,土体与围护墙之间的摩檫力使得墙后土体也有上升的迹象,抵消了一部分沉降,因此MC模型的总体沉降值较小,其墙后影响区域也小于PH模型。为选取合理的本构模型,通过选取不同本构模型进行数值模拟计算,土层参数如表2所示。对比计算结果和实测结果发现,无论是从地表沉降规律(图7)还是建筑物沉降规律(图8)来看,发现PH模型在深基坑中更符合实际情况,故采用PH模型进行模拟。

表2 土层参数Table 2 Soil parameter

图7 不同模型下地表沉降Fig.7 Building subsidence under different models

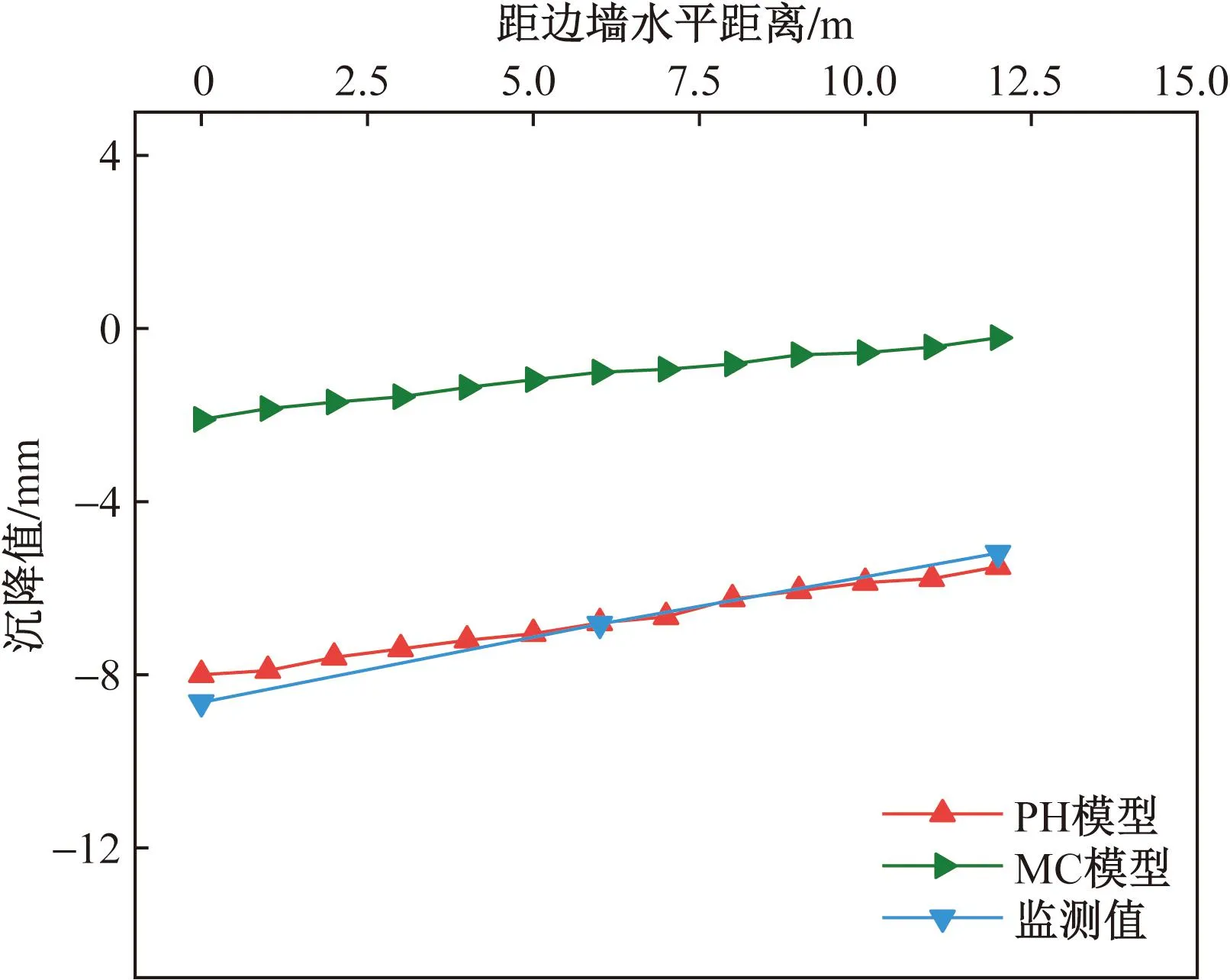
图8 不同模型下建筑物沉降Fig.8 Building subsidence under different models

2.3 数值模拟方案

烈士陵园站围护结构采用钻孔灌注桩,桩孔直径为1 000 mm,桩长25 m,在桩外设置800@450 mm高压旋喷桩止水帷幕。为简化计算,钻孔灌注桩简化为600 mm厚度的地下连续墙,采用实体单元模拟并设置为不透水。为反映基坑开挖过程,将R2线和M1线分为五层进行开挖,先开挖R2线基坑第一层,施做横撑;后开挖M1线第一层,施做横撑,以此类推,当开挖到地下水时,先将水位降低至开挖面以下1.5 m,之后再进行开挖。

3 数值模拟结果及对比分析

3.1 地表沉降分析

数值模型选取的监测线位置和平面布置与图2一致,如图9所示。L1、L2、L3及L4为测点位置,其中L1地表上无建筑物,而L2、L3和L4的地表上均有建筑物。可以看出,地表沉降曲线在建筑物基础的影响下,由圆滑的倒“C”型出现了折线形区域,而其区域恰恰就在建筑物的覆盖范围之中。对比L1～L4可以发现,越靠近东侧的地表沉降越小,这是由于东侧靠近基坑转角三角区,该区域围护桩数量加密以及坑角效应,使得土体的变形相对较小。同时,可以发现地表最大沉降位置基本不变,位于围护结构桩后13.6 m附近,存在建筑物和不存在建筑物对比时,存在建筑物的地表曲线最大沉降值有所减小,这是因为建筑物基础和土体结合相对提高了该区域的土体刚度,使得基坑墙后的建筑区域范围的沉降量有所减小。同时说明建筑物基础的存在与地表沉降曲线确实相互关联,即建筑物改变了地表沉降曲线,地表沉降导致了建筑物的变形。此外,天然地表曲线L1与实测数据的Gauss拟合曲线相差不大,基本符合沉降特征,也反映了数值模拟的准确性。

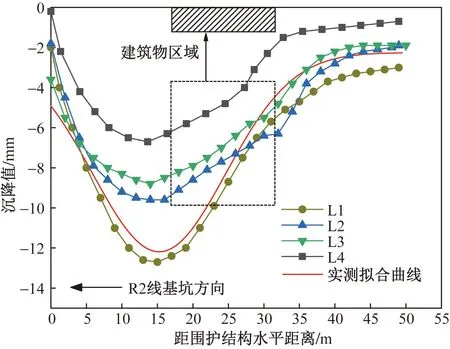
图9 模拟条件下地表沉降Fig.9 Surface subsidence under numerical simulation conditions

3.2 围护结构水平位移分析

围护结构的水平位移和坑外地表沉降存在线性关系,而地表沉降又对邻近建筑物产生影响,说明围护结构变形和建筑物沉降两者存在关联,因此,对围护结构的变形进行分析是很有必要的。

图10为数值模拟条件下围护桩水平位移,可以发现随着围护桩越接近长条基坑中部,围护桩的水平位移也随之增大,呈现向坑内凸出趋势,最大位移处于桩身中部,桩顶端产生较小的位移,桩底部位移基本不变,CX1桩身产生的水平位移最为显著,最大水平位移为22.9 mm。桩身顶端水平位移较小的主要原因是因为基坑安装了冠梁以及钢支撑,其能够显著地约束围护桩的水平变形,但随着基坑开挖到深处,其约束作用开始变小,因而在桩身中部产生的较大的变形,又由于桩底的岩层为风化的岩石,抗变形能力较强,所以桩的底部水平位移基本不变。对比围护结构水平位移监测值(图3),数值模拟反应的规律和实测值大体一致,但模拟值略大于实测值,这是因为一方面由于开挖过程的场地限制,无法完全按照施工组织设计进行施工;另一方面,坑外布置了回灌井,当坑外地下水大量流失时能够得到及时的补充,降低了由于地下水流失而造成的土体变形,而数值模拟没有考虑到回灌措施、降雨等。总体来说,尽管数值上存在误差,但模拟值的曲线发展趋势还是和实测值基本一致。

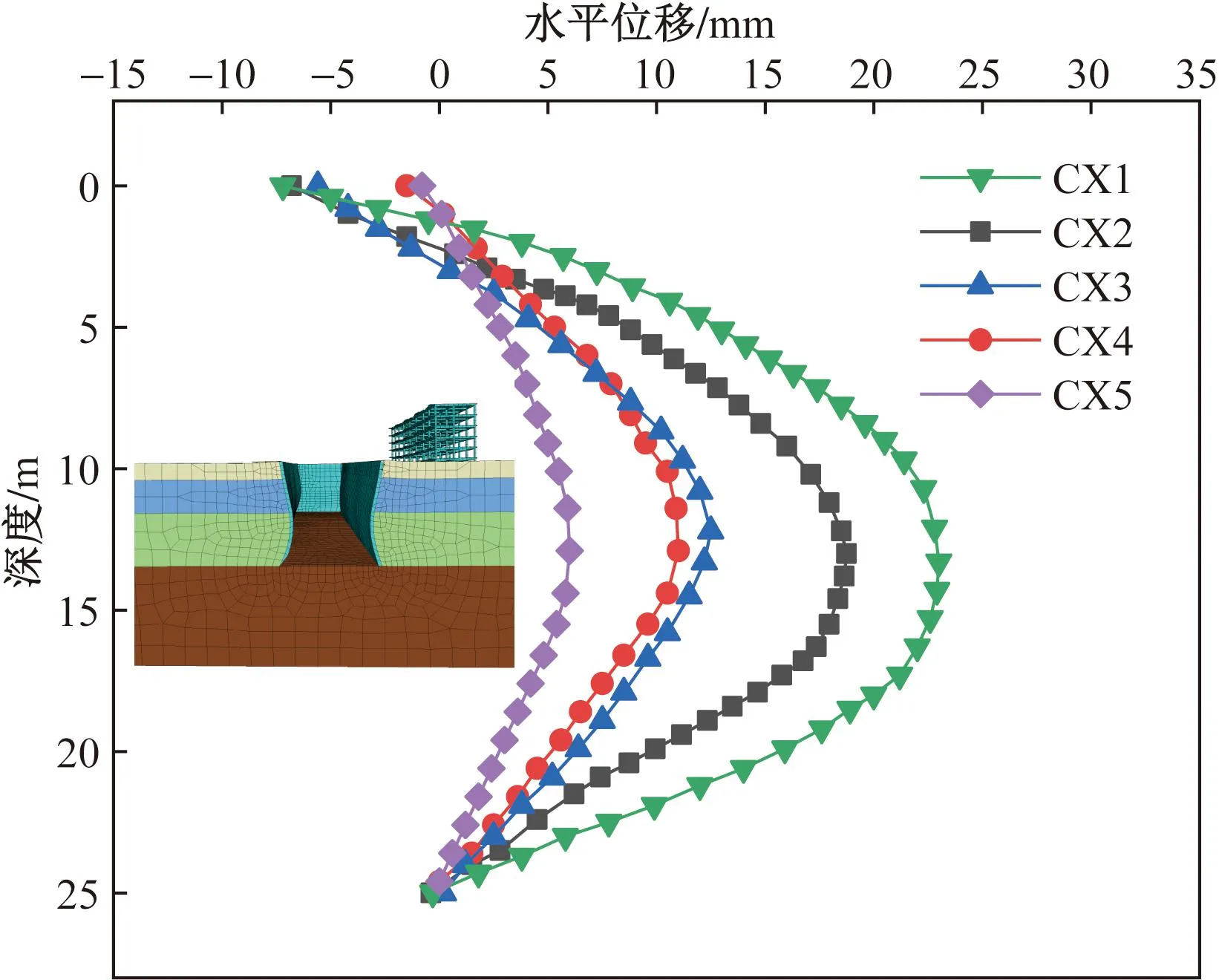
图10 数值模拟条件下围护桩水平位移Fig.10 Horizontal displacement of retaining pile under numerical simulation

3.3 建筑物变形分析

建筑物的位置点不同,其产生沉降值也有所不同,故会造成不均匀沉降和倾斜,建筑倾斜度通常分为水平倾斜和垂直倾斜,由于基坑开挖产生的竖向位移远大于水平位移,故只考虑垂直倾斜,不考虑水平倾斜。

数值模型建筑物的测点与实际监测点一致,为JZ1～JZ8,其沉降过程图如图11所示,累计沉降值如表3所示。可以发现,基坑一开始开挖深度较浅时,建筑物的沉降值较小,随着基坑降水和开挖深度的增大,建筑物的沉降也随之增大,基坑开挖与降水所造成建筑物的沉降大致相当。建筑物总体往基坑方向倾斜,沉降差异的最大两个点为JZ8和JZ4,建筑物的最大倾斜度为0.000 12,与实测值大致相同。对比实测建筑物沉降值,模拟值比实测值偏大,这是因为数值模拟没有考虑到坑外进行地下水的回灌措施,从而导致了这一结果,同时也说明地下水的回灌能够降低邻近建筑物的沉降值。

表3 建筑物实测与数值计算沉降值Table 3 Actual settlement value of the building and the numerical calculation settlement value

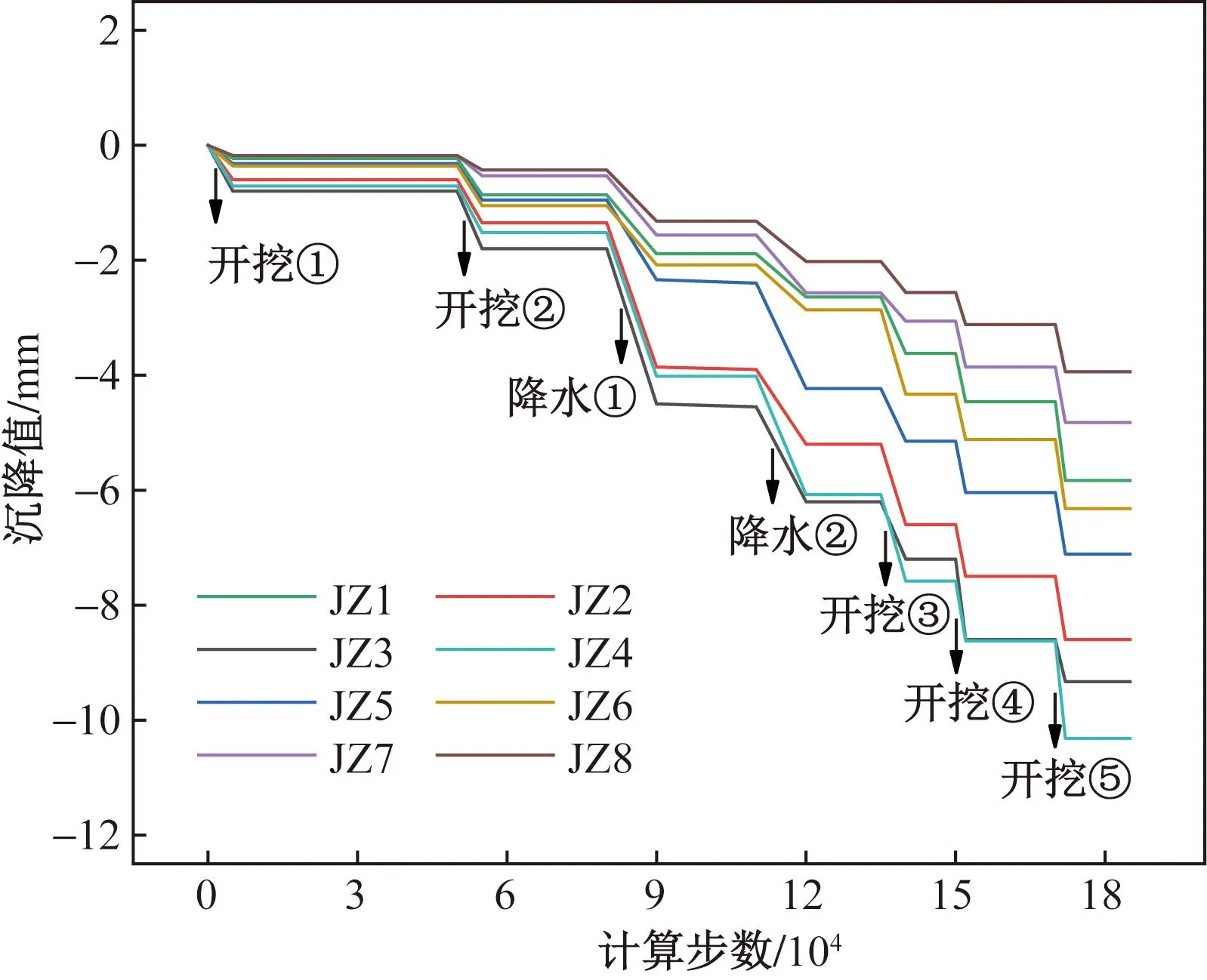
图11 建筑物沉降随计算时间的变化规律Fig.11 Settlement variation of buildings with calculation time

4 不同因素对建筑物沉降规律影响

4.1 钢支撑间距

从土体卸载方面看,围护结构的水平变形与建筑物沉降关联密切,因此需要控制围护结构的变形,分析不同钢支撑间距对建筑物沉降产生的影响,来进一步探讨建筑物的变形规律。由实测数据和模拟结果可知,围护桩的变形主要在中部最为凸出,所以仅对第二道钢支撑的间距进行加密,以此来探讨建筑物沉降情况的变化。

基坑第二道钢支撑间距原设计值为3.0 m,以每0.2 m的变量控制刚支撑间距,对其进行三维数值模型计算,得到不同钢支撑间距条件下建筑物的沉降规律,如图12所示。可以看出,随着钢支撑间距的减小,建筑物的沉降值也逐渐减小,靠近基坑一侧从最大值9.16 mm减小至6.85 mm,远离基坑一侧最大值从6.08 mm减小至5.45 mm,此外,可以看出建筑物的倾斜度也逐渐减小。当钢支撑间距从3.0 m减小至2.8 m时,可以发现建筑物的沉降值显著减小,最大沉降值从9.16 mm减小至7.78 mm,沉降值减小了15%;但钢支撑间距从2.8 m减小至2.6 m,最大沉降值从7.78 mm减小至7.21 mm,沉降值仅减小了7%,钢支撑对减小建筑物沉降的效果开始降低;钢支撑间距为2.6～2.0 m时,沉降值分别减小了2.8%、1.6%、0.7%,可以发现钢支撑对减小建筑物沉降的效果已经很小了。因此,在工程造价和保护邻近建筑物两方面的因素下综合考虑,基坑施工时第二道钢支撑间距可适当减小,建议选择2.6～2.8 m。

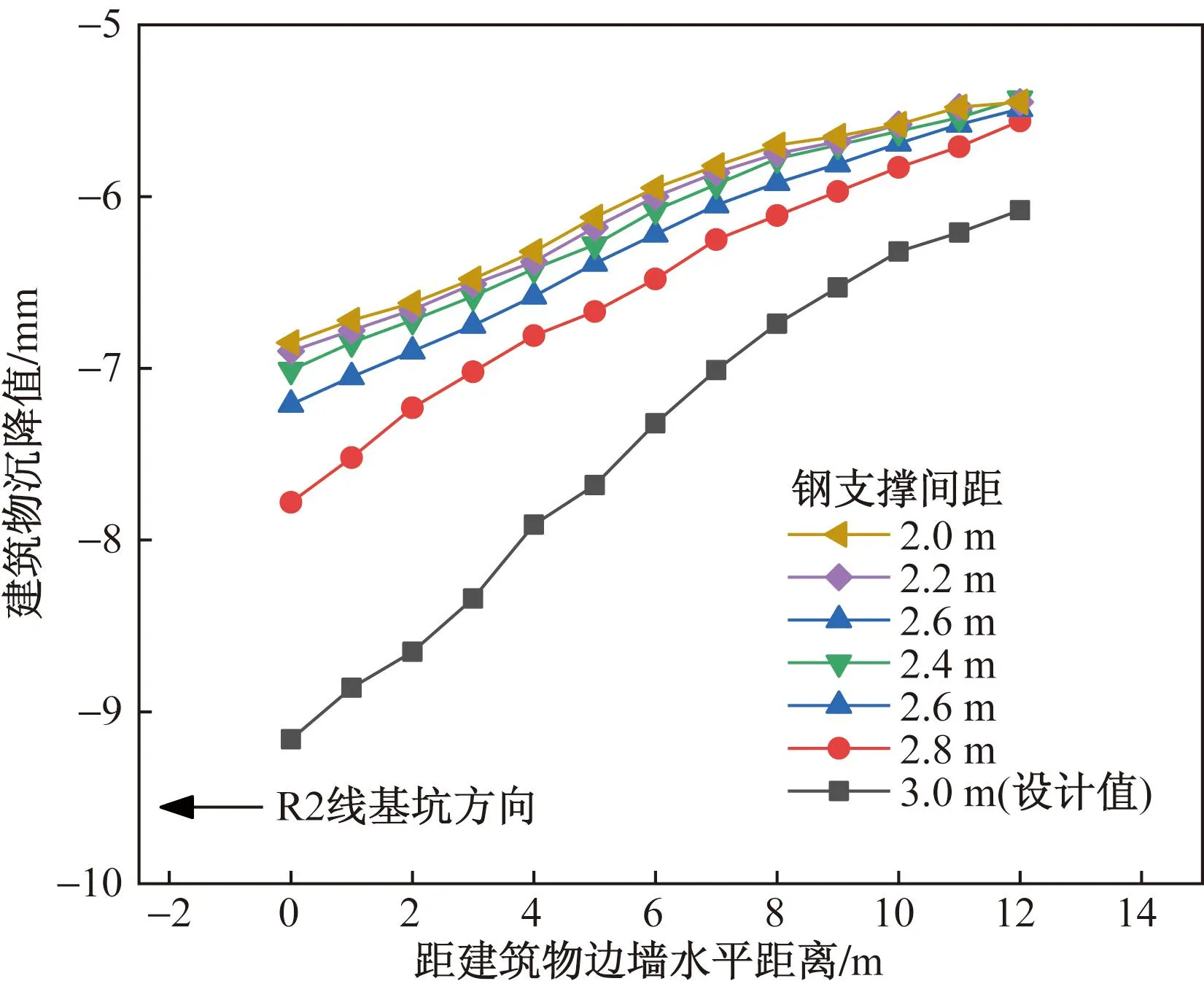
图12 不同钢支撑间距条件下建筑物沉降变化Fig.12 Settlement changes of buildings under different steel support spacings

4.2 止水帷幕深度

为保证邻近建筑物安全,富水地层基坑往往需要阻断坑内外地下水的联系,止水帷幕在基坑施工中起到重要作用,过短的止水帷幕不能起到完全隔断地下水的作用,容易导致地下水渗漏。而过长的止水帷幕造价成本较高,容易形成浪费,因此探究合适的止水帷幕深度能够对施工起到优化作用。

由于基坑开挖深度为22 m,一般来说止水帷幕深度应大于开挖深度,因此,模型中的止水帷幕深度分别设置为25、27.5、30、32.5、35、37.5、40 m以及无止水帷幕。经过计算,得到不同止水帷幕深度条件下邻近建筑物的沉降规律,如图13所示。可以看出,建筑物沉降随着止水帷幕插入深度增加出现减小的趋势,从25 m开始,止水帷幕插入度每增加2.5 m,建筑物最大沉降值分别减少0.11、0.49、0.14、0.09、0.05、0.04 mm。当止水帷幕插入度为25～27.5 m时,对减小建筑物沉降值效果较小;当止水帷幕插入度为27.5～30 m时,对减小建筑物沉降值效果较明显;当止水帷幕插入度为30～40 m时,对减小建筑物沉降值效果又开始降低;当坑外无止水帷幕时,建筑物的沉降量最大为-10.21 mm。主要原因为:由于地表以下25 m处为全风化闪长岩,可视作隔水层,止水帷幕插入地下25 m形成封闭式止水帷幕,切断了坑内外地下水联系,此时止水帷幕能够起到减小建筑物沉降的作用。但全风化岩石存在许多裂隙,不能完全阻断坑内外地下水联系,直到止水帷幕插入到地表下30 m处,此时止水帷幕到达了强风化闪长岩,相对全风化闪长岩隔水性更好,所以起到降低建筑物沉降的效果更明显。地表30 m再往下为隔水性更好的闪长岩,此时坑内外地下水联系已绝大部分阻断,止水帷幕深度再增加对减小建筑物沉降的效果已开始降低。因此,建议止水帷幕的深度控制在27.5～30 m。

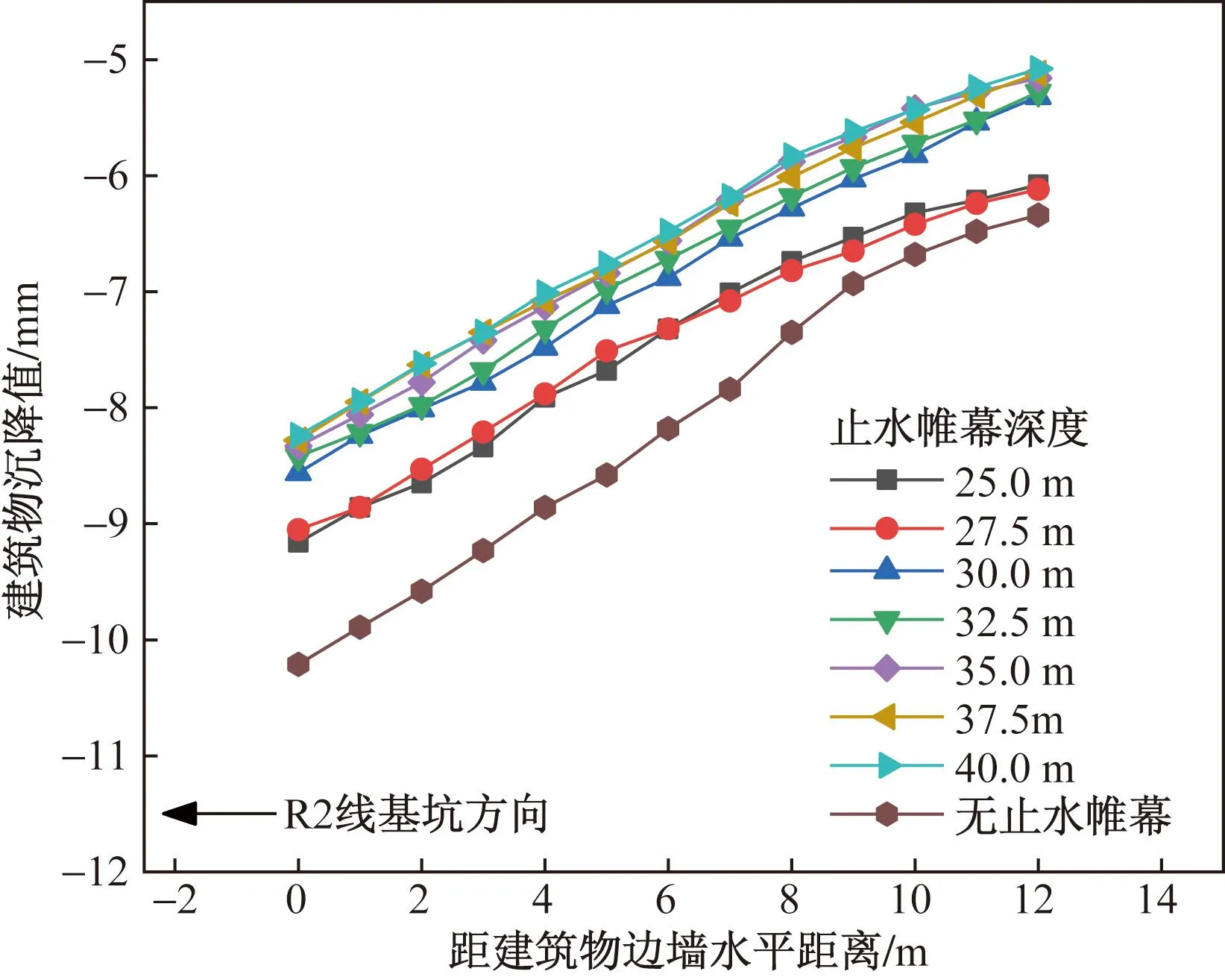
图13 不同止水帷幕深度下建筑物沉降变化Fig.13 Settlement variation of buildings under different waterproof curtain depths

5 结论

以济南地铁烈士陵园站深基坑为工程背景,采用现场实测与数值模拟相结合分析深基坑施工对邻近建筑物变形规律的影响,并探讨不同因素对邻近建筑物变形的影响,得出如下结论。

(1)建筑物与地表沉降曲线之间相互关联,建筑物的存在不会改变地表的沉降趋势,但在建筑物覆盖的地表会因为建筑物基础的刚度比土体大而产生折线形的地表曲线;坑外建筑物的变形主要是由于地表沉降而导致的。

(2)基坑开挖和降水引起建筑物的沉降量大致相当;基坑外设置回灌井进行回灌能够降低建筑物的沉降值,由于施工时进行了回灌措施,因此地表沉降、围护结构变形和建筑物沉降的监测值均符合规范要求。

(3)建筑物沉降随着钢支撑间距减小而减小,当间距减小到2.6 m时,其效果开始降低,因此选择2.6～2.4 m的钢支撑间距,可以起到对周边建筑物较好的保护作用。

(4)建筑物沉降随着止水帷幕深度增加而减小,当止水帷幕插入到30 m时,其效果开始降低,建议选择27.5～30.0 m的止水帷幕深度,能够降低施工成本,获得较好的经济效益。