考虑学习效率的教室内热环境调控系统研究
王晓辉, 李兆巍, 杨亚龙
(1.北京建筑大学电气与信息工程学院, 北京 100044; 2.安徽建筑大学智能建筑与建筑节能安徽省重点实验室, 合肥 230022)
教室作为学生日常学习的主要场所,其环境的优劣对学生来讲十分重要[1-4]。文献[5-9]研究表明,教室环境会影响学生舒适程度的同时,也会影响学生的学习效率。随着科学技术的不断发展,室内热环境调控系统已成为当前研究的热点之一,而如何利用人工智能技术设计智能控制策略,提高室内空气质量和舒适度、减少能耗已经成为研究重点。
文献[10]基于机器学习对3种不同通风方式的室内控制策略分别进行能耗测试,实验结果建议在设计调控系统时应增加受控设备的多样性,以达到节能的目的。张明扬[11]采用机器学习算法,以新有效温度为舒适指标,提出基于热适应的绿色建筑环境智能控制系统,实现了对室内热环境的智能控制和优化,该系统可以提高建筑的舒适度,减少能耗污染。文献[12]系统地总结了智能建筑热环境调控系统的研究进展,指出人工智能技术对于室内热环境调节的准确性和预测性起到了重要的作用。文献[13]利用神经网络构建自启发算法,提出一种适用于学校的智能暖通空调控制策略,可自适应调节供暖等设备的工作状态。
研究人员为更快速、准确地获取当前热环境数据进行了详细研究。文献[14-15]尝试将个人热舒适模型应用于室内热环境调控系统中,实现个性化的室内热环境控制,提高用户满意度。文献[16-17]对互动式界面收集个性化人体热感觉数据这一重点展开研究,以完善智能建筑的热环境控制方案,提高用户的接受度。文献[18-19]则是通过使用生理参数识别技术预测人体的实时热感觉,以解决调控热环境设备实际运行情况与用户实际热感觉脱节的问题。
同样地,针对调控系统的具体控制方式,也有大量的相关研究。韩雪颖通过感知收集室内的环境参数,利用模糊控制方法,实现对室内空气质量等参数的智能控制[20]。蒋延炜[21]通过对人体热舒适指标预测平均投票值(predicted mean vote,PMV)进行监测调整,采用模糊比例积分微分(proportion integration differentiation,PID)控制算法实现了对室内热湿环境的智能控制。文献[22]针对气候变化对养老建筑的热环境动态调节进行研究,提出了一种基于建筑热环境的动态控制方法,通过预测气象条件和分析室内环境参数来实现智能化控制。
综上所述,现今室内热环境调控系统主要面向数据采集、对室内热环境情况进行预测、具体控制方式等方面进行研究和优化。然而现阶段,针对教室这一以学习效率为关注点的特定场所,室内热环境调控系统的研究较为空白,这使得加强教室内热环境调控系统的设计变得十分紧迫。
鉴于此,以学习效率为出发点,兼顾热舒适度,设计一套教室内热环境调控系统。采取直接和间接相结合的方式来调控PMV,直接控制PMV的主要影响因素如温度、风速和相对湿度,以达到间接调控PMV的目的。提出基于粒子群优化的BPNN(back propagation neural network)模型来预测PMV值,以便及时响应当前的热环境。通过量化学习效率与PMV之间的关系,以及考虑各热环境相关物理量的舒适范围,确定调控方案的控制目标。提出BP-PID控制算法对各环境参数进行调节,以实现调控室内热环境的目的。最后,通过系统仿真模拟,对比调控前后的室内热环境和学生学习效率,证明该方案的有效性。在使学生感到舒适和使其学习效率维持较高水平间找到平衡,设计出了一套室内热环境调控系统,为积极推进智慧教室的建设提供了有效依据。
1 室内热环境调控系统介绍
1.1 调控系统概述
选取在国际上认知度较高、且应用最为广泛的评价热舒适度指标PMV作为室内热环境的评价指标[23]。PMV的主要影响因素包括4个环境因素:温度、风速、相对湿度和平均辐射温度,考虑对PMV影响程度以及控制的可操作性,选取前三者作为调控方案的控制对象。
对PMV的控制目前分为直接和间接控制两种方式,其中直接控制是将PMV直接作为控制目标,间接控制是将温度等环境物理量作为控制目标,而PMV仅作参考。不同于上述两种,采用直接与间接相结合的控制方式,将当前热环境状态与PMV设定目标进行对比,通过直接控制温度、风速和相对湿度3个环境物理量,达到间接控制PMV的最终目标。
所设计的室内热环境调控系统在运行过程中实时采集当前的热环境相关参数(温度、风速以及相对湿度),准确、快速地计算出当前的PMV,进而以此为依据,判断是否需要对当前室内热环境进行调控。若需要,则自动计算温度、风速以及相对湿度的调控目标值,通过控制器对各个模块分别进行调节,并进行实时反馈。
1.2 调控系统构成
所设计的室内热环境调控系统结构如图1所示,系统所包括的4个模块及其所实现的功能如下。
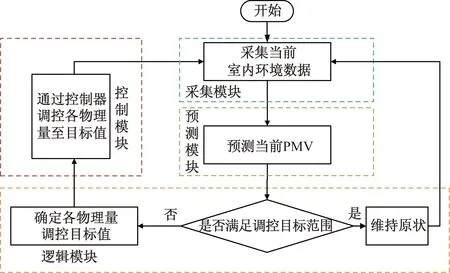
图1 室内热环境调控系统结构图Fig.1 Structure of the indoor thermal environment control system
(1)采集模块。通过传感器实时采集当前热环境数据(温度、风速和相对湿度),便于与调控目标进行对比。
(2)预测模块。通过粒子群改进的BPNN对PMV进行预测,便于实时获取当前PMV。
(3)逻辑模块。综合考虑当前热环境情况和调控目标范围,通过逻辑推理确定各物理量的调控目标。
(4)控制模块。在确定各物理量调控目标的基础上,通过BP-PID控制器对各环境物理量进行调节,使其达到目标值。
2 室内热环境调控系统设计
2.1 基于PSO-BP的PMV预测模型的构建
由于PMV的传统计算方法存在参数相互耦合和计算量大的问题,因此考虑采用适当的模型对PMV进行实时预测。虽然BP神经网络结构简单、对复杂非线性函数具有良好的学习和预测的能力,但仍然面临学习速率慢和网络结构不确定性等缺陷。而粒子群优化(particle swarm optimization,PSO)算法能够通过信息共享在全局中搜索最优权值阈值,以此来优化BPNN的初始化权重阈值,解决其过拟合问题,提高了收敛速度和网络性能稳定。因此,采用PSO对BPNN进行优化,即PSO-BP,以提高对PMV预测的精度和效率。
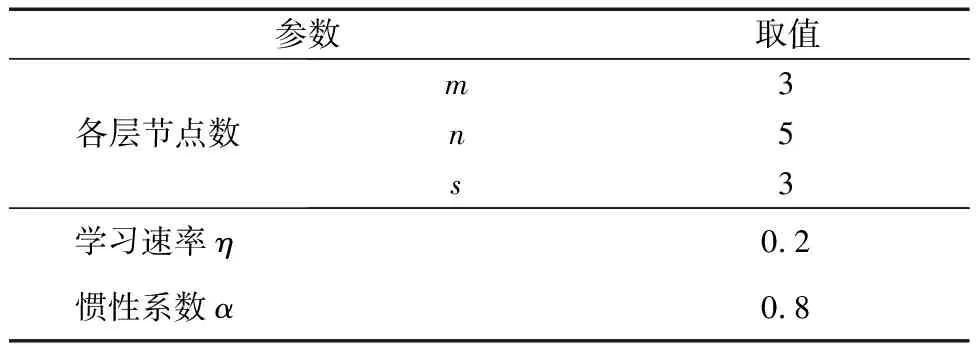
首先确定粒子群优化算法的基础参数。根据预测的PMV指标特点,综合考虑通用预测模型的参数取值范围,确定采用的PSO-BP算法的基础参数如表1所示。

表1 PSO-BP预测模型参数设置Table 1 PSO-BP prediction model parameter settings
实验数据由实验室中各类传感器采集所得,经过筛选处理后共得到631组样本数据。将数据划分为两组:其中531组数据作为训练组,用于对网络模型进行训练;另外100组数据为测试组,用于测试该模型对PMV的预测性能。
对BPNN和PSO-BPNN两个模型分别进行训练并测试,结果如图2所示。可以看出,PSO-BPNN预测模型与真实值的拟合程度相对传统BPNN更高,说明经过PSO优化后的模型预测精度更高。

图2 PSO-BPNN对PMV的预测结果Fig.2 Predicted results of PSO-BPNN for PMV
表2详细比较了两种预测模型的精确度,可以看出,对于PMV的预测结果,PSO-BPNN 比BPNN预测模型的平均绝对误差降低了80.10%,均方误差和均方误差根仅为改进前的3.78%和19.42%。综上所述,PSO优化后的BPNN模型对PMV的预测效果更好,可应用至调控系统的设计中。
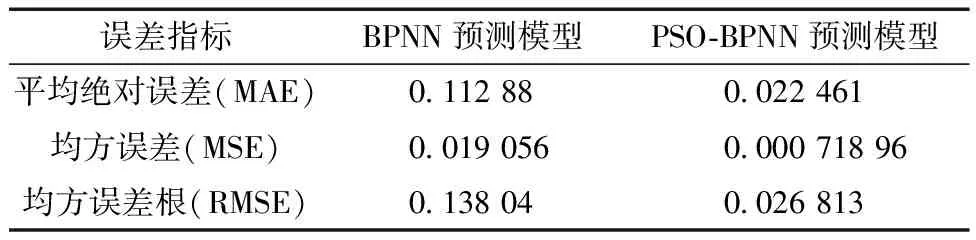
表2 两种预测模型误差指标对比Table 2 Comparison of the error metrics of the two prediction models
2.2 控制目标的逻辑确定
为使调控系统实现调节室内环境的作用,首先需要明确调控方案中各个物理量(PMV、温度、风速和相对湿度)的调控目标(范围),继而再通过控制模块使其达到目标值。
在设计调控系统之前,为探究学习效率与PMV的量化对应关系,设计Stroop颜色测试、事件逻辑排序测试、打字速度测试等实验[24],测量不同PMV工况下所对应的学习效率,对实验结果进行回归拟合,确定了PMV与学习效率的拟合曲线为:y=3.030 9-0.244 29x-0.296 2x2,表示学习效率在偏凉爽的时候较高,当PMV=-0.592 4时,被试者的学习效率可达到最高值。
考虑不同地区、性别、生活习惯的学生对室内环境的不同个人偏好,并综合考虑空调系统的节能问题,本调控方案将PMV的控制目标范围确定在-0.59%±5%(-0.619 5
首先需要确定温度、风速和相对湿度的调控范围,参考《民用建筑供暖通风与空气调节规范》(GB 50736—2012)[27]中对空气质量所提出的要求,确定影响室内热环境各物理量的目标范围如表3所示,对于不同典型季节,温度的调节目标区间有所变化。

表3 影响室内热环境各物理量目标区间Table 3 Target intervals for each physical quantity affecting the indoor thermal environment
基于以上各物理量目标区间,本调控系统中逻辑模块的策略如图3所示。
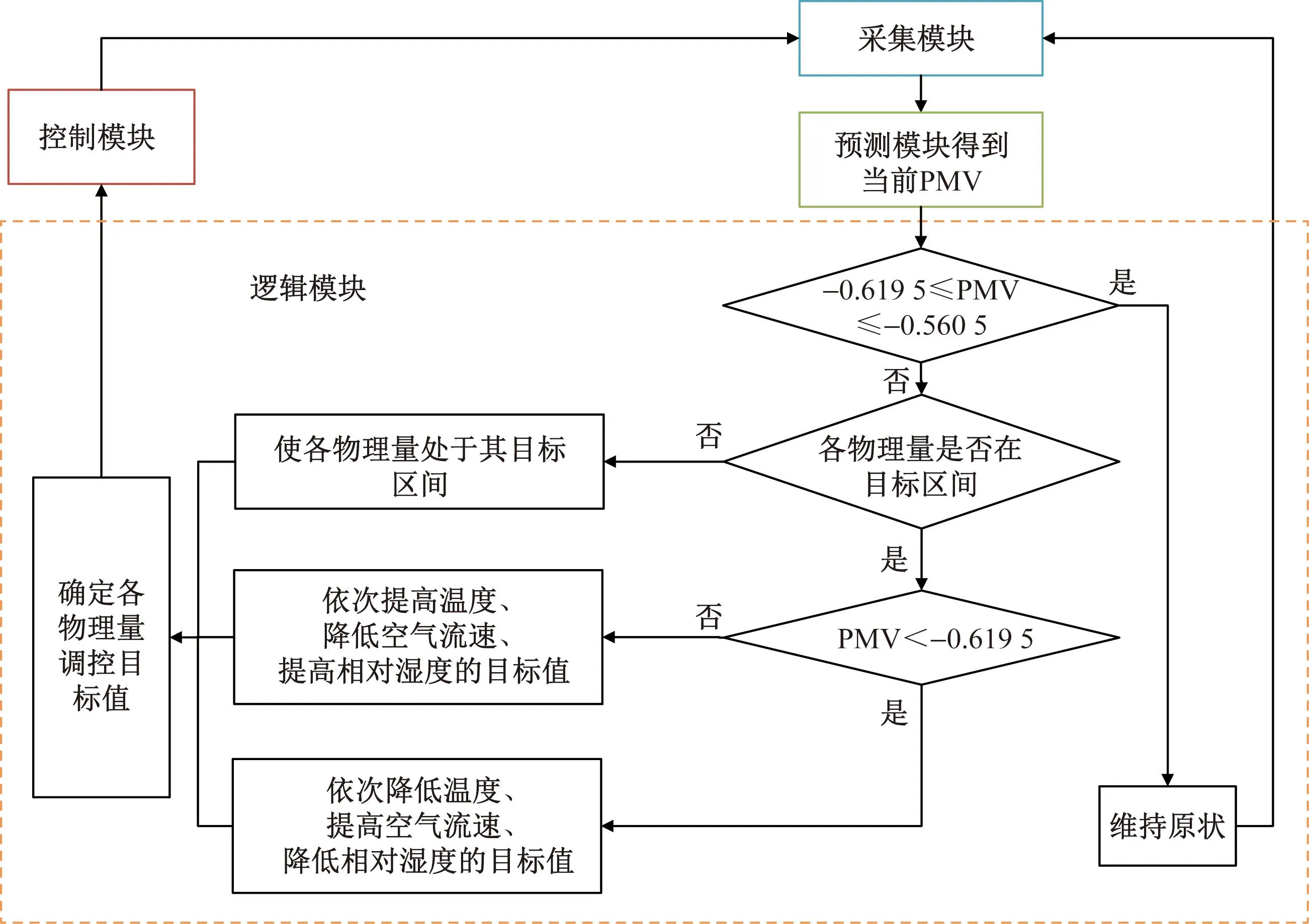
图3 逻辑模块流程图Fig.3 Flow chart of the logic module
首先,实时采集室内环境数据,并通过实时预测当前PMV值,随即进入确定控制目标的逻辑环节:若PMV在目标范围内,即-0.619 5 根据目标范围依次调整温度、风速和相对湿度至各自目标值。如果值大于目标区间最大值,则调整至目标范围最大值。如果小于目标区间最小值,则调整至目标范围最小值。 将PMV与目标范围进行比较。在PMV与设定目标相差较多时,先降低温度;在对接近目标范围的PMV值时减少相对湿度。如PMV>-0.560 5时,则逐步地降低室内温度、提高风速、减少相对湿度的控制目标以减小PMV。PMV<-0.619 5时同理。 确定各物理量的控制目标后,通过控制模块对温度、风速和相对湿度进行调控。再次采集实时室内环境数据,并重复执行上述步骤以不断调节室内环境。 确定3个环境因素的调控目标,进一步地,需要确定如何使其达到该目标值。PID控制算法具有算法简单、鲁棒性好、可靠性高等优点,尤其适用于可建立精确数学模型的确定性控制系统[28]。 影响PID控制器性能的主要因素是比例系数Kp、积分系数Ki和微分系数Kd三者的组合方式,但这种组合关系不一定是简单的线性组合,大部分情况下,最佳组合方式存在于变化无穷的非线性组合中。BPNN具有任意非线性表达的能力,可以通过有效地学习系统性能来获得具有最佳参数组合的PID控制器。因此,研究人员将其与PID控制结合起来,开发了基于BPNN的自学习PID控制器,即BP-PID控制器[29]。 BP-PID控制器可根据系统的偏差e(t),通过神经网络自学习,采用梯度下降法调整加权系数,使BPNN的输出对应于PID控制器的3个可调参数,实现比模糊规则更稳定的PID参数自适应调整,使系统输出尽快达到给定值,适应性更强,更为灵活。 BPNN是一种按照偏差逆向传播算法训练的多层前馈神经网络,在结构上分为输入层、隐含层和输出层,每层节点数不同,具体模型参数如表4所示。 表4 BP-PID中的BPNN模型参数设置Table 4 Parameter settings for the BPNN model in BP-PID 针对前述进行学习效率实验的场地,继续展开室内热环境的研究,具体参数如下:房间尺寸为7.5 m(长)×4 m(宽)×3.75 m(高),窗面积6.75 m2,传热系数2.3 W/(m2/K),外墙面积9.375 m2,传热系数0.583 W/(m2/K)。房间内室内环境依靠集中式空调系统进行调控,空调距地1.85 m。 根据室内湿量守恒定律得到空调房间湿度模型G1(s)为 (1) 式中:s为复频率。 同理可求风速模型G2(s)为 (2) 温度模型G3(s)为 (3) 在MATLAB/Simulink中搭建仿真模型,对上述BP-PID控制器的控制效果进行仿真模拟。将以湿度模块为例,详细对比3种PID控制器(传统PID、模糊PID和BP-PID控制器)的控制效果。 将控制目标的相对湿度设定为65%,详细对比3种不同控制器的控制效果,得到各阶跃响应曲线如图4所示。可以看出,3种不同PID控制器的阶跃响应曲线大致走向均是先快速升高至达到最大值,随后开始下降,可能会低于调控目标(传统PID控制器),最后通过细微调整使被调控量逐渐稳定在调控目标值附近。 图4 相对湿度阶跃响应曲线Fig.4 Step response curve for relative humidity 为了更清晰地体现该控制算法的优越性,选取控制系统评价指标的参数进行详细分析,如表5所示。由表5数据可知,BP-PID比传统PID和模糊PID控制器在调节时间上分别减少了74.25%和73.63%,超调量也减小至原本的85.01%和89.64%。综上所述,BP-PID控制器的超调量更小,峰值时间和调节时间也较短,证明了所设计的BP-PID控制器在稳定性和快速性上表现良好,可用于室内热环境调控系统的控制模块中。 表5 BP-PID与传统PID及模糊PID控制效果的比较Table 5 Comparison of the effect of BP-PID with conventional PID and fuzzy PID control 后续调控方案效果研究中,将上述室内热环境模型作为表示输入与输出间数量关系的函数,在确定BP-PID控制器的输入后,输出就可以根据该模型和输入运用拉普拉斯反变换方法确定。在实际应用中将其作为传递函数导入Simulink,实现在MATLAB中的仿真模拟。 为探究本文所设计的调控系统性能,在软件中进行仿真模拟,记录温度、风速、相对湿度及PMV在经过本调控系统调控前后的数值进行对比。通过传感器采集室内环境数据作为初始数据,根据典型季节将数据划分为冬季、夏季以及过渡季,选取每个典型季节10组、全年共30组用于仿真模拟,部分样本数据如表6所示。 表6 部分仿真数据样本Table 6 Selected sample simulation data excerpts 在MATLAB/SIMULINK中建立室内热环境调控系统的仿真模型,如图5所示(其他季节仅自定义函数模块内部数据设定不同,但仿真模型结构未变)。首先,使用传感器采集温度、风速和相对湿度3个物理量的实时值treal、vreal、hreal,并采用PSO-BPNN实时预测当前的PMV值。通过确定控制目标模块得到各模块的调节目标值tset、vset、hset,进入控制模块。该模块中,通过BPNN自学习来调节PID控制器的3个参数,经过传递函数得到当前环境状况,即3个环境物理量的实时值treal、vreal、hreal,通过PSO-BPNN再次预测PMV值,并将实时值反馈给逻辑推理部分,进而再次循环以达到动态控制的目的。 treal、vreal、hreal和PMVreal分别为传感器采集温度、风速、相对湿度和PMV的实时值;tset、vset、hset分别为通过确定控制目标模块得到各模块的调节目标值;fcn为预测和逻辑模块部分的自定义函数;pmd 为预测模块部分的自定义函数;r(k)、y(k)和u(k)分别为BP-PID控制器的给定量、输出和被控系统输出;Scope1、Scope2、Scope3和Scope分别为可以显示温度模型、风速模型、湿度模型和PMV的示波器图5 室内热环境调控方案仿真模型Fig.5 Simulation model of an indoor thermal climate control scheme 为详细观察调控系统的实时控制效果,选取一组数据(温度为21.2 ℃,风速为0.1 m/s,相对湿度为33.4%)分析其PMV的实时变化,如图6所示。图6(a)~图6(d)分别为温度、风速、相对湿度和PMV的阶跃响应曲线,温度、风速和相对湿度的调节时间依次为2.571、1.469、753.285 s,PMV的走势先快速上升,后上升速度明显减慢,逐渐靠近PMV的目标范围,最终维持在-0.564 7,调节时间取决于所需稳定时间最长的相对湿度。 根据PMV与学习效率的解析关系可以估算出调节前,即PMV=0.184 2时,学习效率为2.975 85;经过热环境调控方案调节后,PMV=-0.564 7,学习效率为3.074 40,提高为原来的103.312%。 通过对所选取的某一组数据进行仿真,详细计算了调控系统工作过程中各物理量的变化过程。为进一步研究调控系统的普适性,对全部的样本数据进行仿真模拟,得到调控前后的各环境物理量及其控制目标范围的对比以及调控前后学习效率的对比,如图7所示。 横坐标数据1~10为夏季;11~20为过渡季;21~30为冬季图7 调控前后各量对比Fig.7 Comparison by volume before and after regulation 图7(a)和图7(d)可以看出,现有高校教室内的热环境相较调控目标偏暖,尤其夏季和过渡季,冬季室内PMV与目标相差最小,甚至有些情况下不需要对当前室内热环境做出调整。图7(b)和图7(c)表示自然情况下教室内普遍存在无风感、较为干燥的现象,在实际生活中略微风感和恰当的湿度会增加学生在教室中的舒适程度,因此针对风速和相对湿度同样进行了调整。 从图7(a)~图7(d)中可以看出教室内热环境在经过系统调控后,各环境物理量均在系统设计时所提出的控制目标范围内(表3)。图7(e)为调控前后的学习效率对比,可以看出热环境调控后的学习效率普遍高于调控前,调节前的学习效率平均值为2.863 6,调节后可以达到3.074 3,平均可提高为原来的107.36%,体现了所提出的调控系统的有效性。 所提出的调控系统中具体的调控参数是基于特定研究场所做实验的结果分析,在不同情况下所得到的学习效率最高时的PMV值可能略有差异,可根据实际所测数据修正调控方案中的调控参数。 针对高校智慧教室,以提高学生的学习效率为目的,兼顾PMV,设计了一套室内热环境调控系统。通过理论研究、仿真模拟以及结果分析得出以下结论。 (1)通过PSO算法对BPNN进行改进,构建出PSO-BPNN模型对PMV进行预测,以解决PMV计算复杂、BPNN网络结构不稳定、易产生过拟合等问题。仿真结果表明PSO-BPNN 比BPNN预测模型在平均绝对误差上降低了80.10%,预测精度更高,将其用于调控系统的预测模块。 (2)通过对PMV的主要环境影响因素进行分析,提出先调节温度,再调节风速,最后通过调节湿度来对PMV进行微调的方案,以确定各环境物理量的控制目标,该部分用于调控系统的逻辑模块。 (3)设计出针对环境物理量的BP-PID控制器,在确定温度、风速和相对湿度控制目标的基础上对其进行调控。仿真结果表明,相较传统PID与模糊PID,BP-PID控制器的调节时间缩短了74.25%和73.63%,超调量也减小至原本的85.01%和89.64%,调控效果更好,并将其应于调控系统的控制模块。 (4)对包含采集、预测、逻辑以及控制4个模块的教室内热环境调控系统进行仿真模拟,结果表明本调控系统可以对温度、风速、相对湿度以及PMV进行有效控制,将学生的学习效率提高到原来的107.36%,在保持舒适性的同时,尽可能地为学生创造良好高效的学习环境,为高校智慧教室的室内热环境调控提供了切实有效的方案。2.3 BP-PID控制器的设计与实现
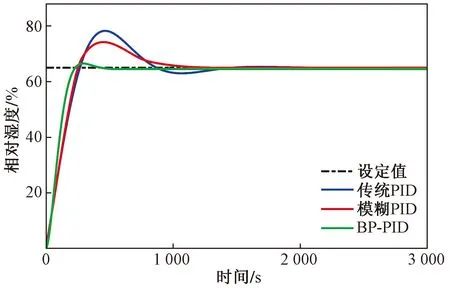
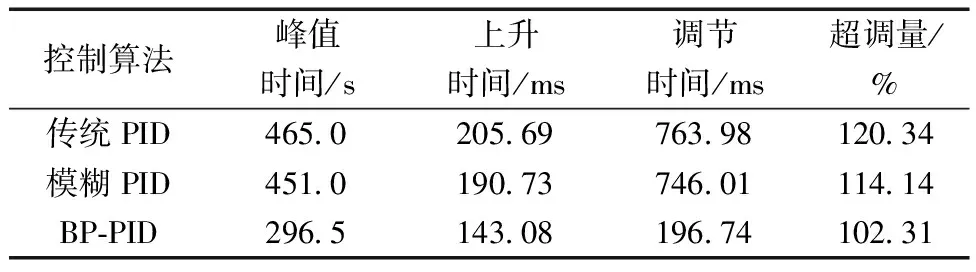
3 室内热环境调控系统仿真分析
3.1 数据来源

3.2 仿真模型
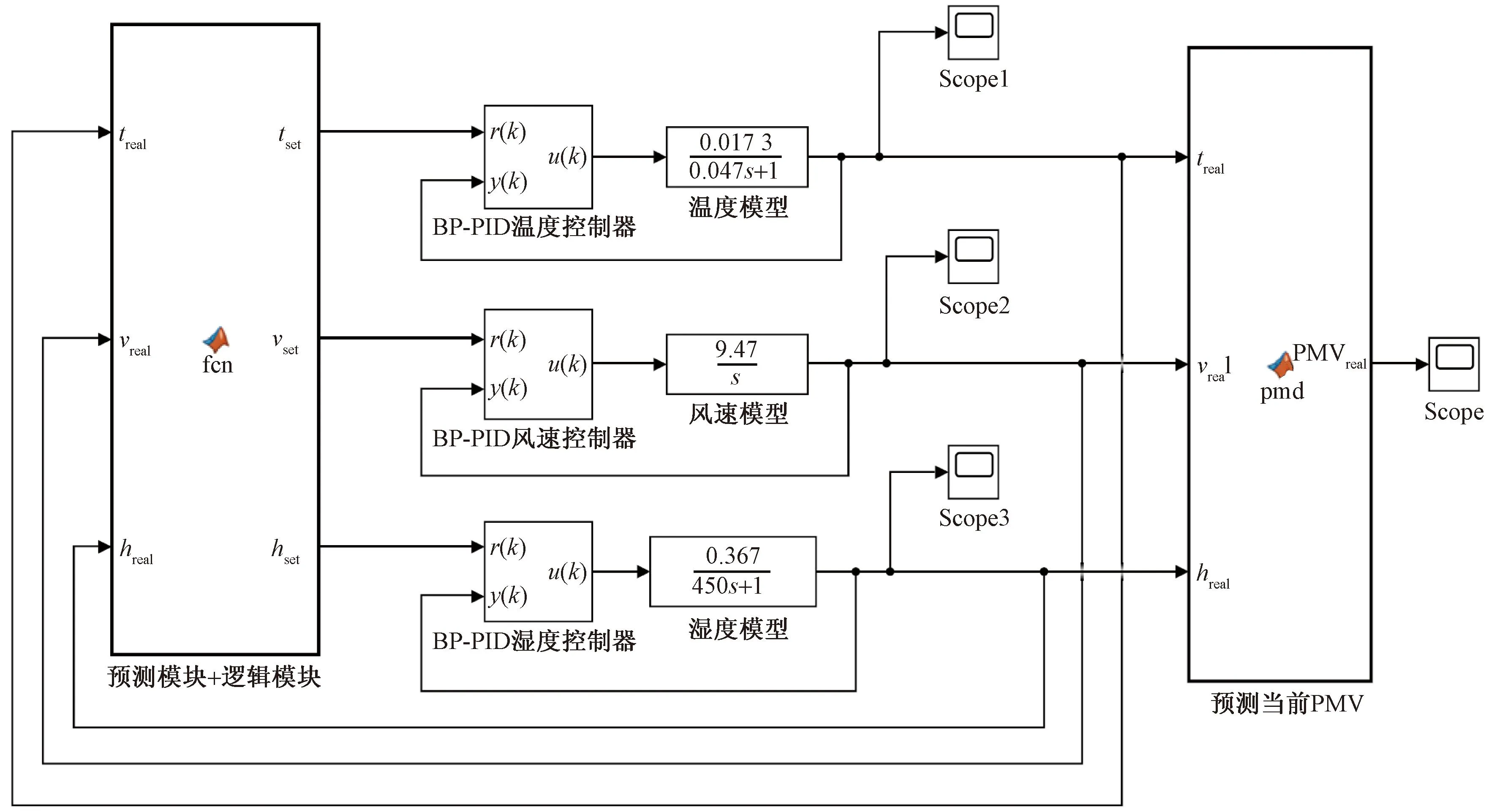
3.3 仿真结果分析
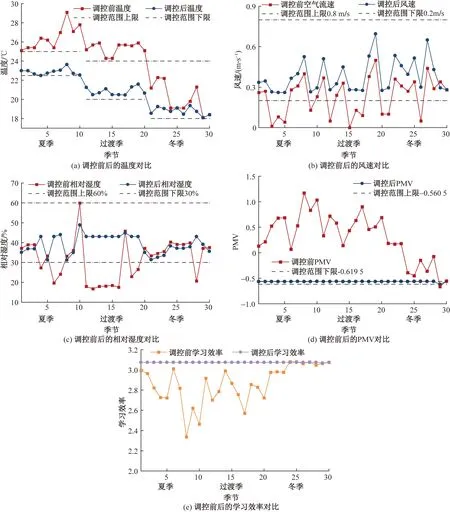
4 结论

