基于双向同态加密的深度联邦图片分类方法

梁天恺，黄康华，刘凯航，兰 岚，曾 碧

（1.广州广电运通金融电子股份有限公司研究总院，广东 广州 510000；2.广发银行信用卡中心资产管理部，广东 佛山 528253；3.广东工业大学计算机学院，广东 广州 510006）

0 引 言

随着智能化终端的普及和人工智能技术的发展，图片分类算法得到了长足的发展，应用场景包括人脸识别和垃圾分类等［1-2］。然而，人们在体验着人工智能算法带来的便利的同时，也产生了对隐私保护问题的担忧，这促使人工智能算法从集中式学习到分布式现场学习再到联邦学习的演变［3-4］。

集中式学习是目前最常见的学习模式，指的是将多个用户的数据集中到主服务器上，并使用主服务器的资源执行机器学习任务，构建人工智能模型［5-6］。特别是深度学习技术被广泛应用于图片分类上。如最为简单的卷积神经网络LeNet［7］，但LeNet 不适用于大规模和复杂的图片分类场景。因此有的学者提出通过加大神经网络的深度或宽度来提高神经网络在大规模和复杂的图片分类场景下的准确率，如VGG［8］和GoogLeNet［9］等；有学者引入残差来提高图片分类任务的可学习空间，如ResNet［10］；也有学者从特征入手，提出密集连接的概念，实现特征重用和减少参数量，如DenseNet［11］。然而，上述算法都属于集中式学习算法，此种“模型不动，数据动”的学习模式使用户数据暴露在主服务器上，无法保护用户隐私，因此催生了分布式现场学习［12］。

分布式现场学习的特点是用户数据在自身边缘的局部范围内构建小的本地模型，以此隔绝用户隐私数据的交换，达到隐私保护的目的［13］。最经典的实现方式是边缘计算［14］。然而，分布式现场学习在隔绝用户隐私数据交换的同时也隔绝了有利于图片分类的特征知识的交换，导致数据孤岛的现象，致使各本地模型的泛化能力较差。

近年来，联邦学习的出现为解决机器学习所存在的隐私保护和数据孤岛问题提供了新的思路。联邦学习的特点是“数据不动，模型动”［15］。联邦学习可被分为横向联邦学习、纵向联邦学习和联邦迁移学习。其中横向联邦学习适用于参与方之间的特征空间差异较小而数据空间差异较大的情况，比如拥有不同类别图片的不同公司用户组成横向联邦学习系统来训练多类别的图片分类模型。此学习模式下，一个用户被视为一个参与方；而主服务器扮演着协调者的角色，不保存任何图片数据。首先，参与方基于本地数据构建本地模型，再将本地模型信息传送给协调方进行安全聚合，然后参与方利用协调方下发的聚合模型信息更新本地模型，有效保证了用户的隐私安全和解决了数据孤岛的问题［13］。近年来也有学者陆续将联邦学习应用到图片处理领域，如王生生等［16］将联邦学习应用于新冠肺炎胸部CT 图片处理。但是，此类算法大多是传统机器学习算法的联邦实现，因此和传统的联邦学习一样在模型聚合过程中存在较大的通信阻滞风险，即协调方需要等待所有参与方的本地模型信息返回后才进行安全聚合［17］，如出现通信不畅或某参与方中途掉线等阻滞现象，则会导致协调方陷入无限的等待中，严重影响联邦学习的效率。其次，由于传统的联邦学习算法过程中的密钥对是由协调方产生并将公钥下发给参与方使用的，因此协调方可使用所拥有的秘钥来解密模型信息的密文，进而反推出参与方的模型或数据特性，存在一定的隐私保护问题。

为解决上述3 种学习模式所存在的问题，本文结合双向同态加密和深度学习技术，提出一种基于VGG 和双向同态加密的联邦图片分类方法，英文名为Federated Image Classification Method Based on VGG and Bilateral Homomorphic Encryption，简称AFL算法。

AFL 算法是深度网络VGG16 的横向联邦实现。其次，针对传统的VGG16 和联邦学习所存在的隐私保护问题，基于Paillier 同态加密［18］算法提出一种双向Paillier 同态加密机制，英文名为Bi-directional Paillier Homomorphic Encryption Mechanism，简称Bi-HE 机制。同时，针对传统联邦学习在模型聚合过程中存在的通信阻滞风险，提出一种自适应的模型聚合等待策略，有效提高了联邦学习的通信阻滞应对能力和自适应能力，提高了联邦学习效率。最后，使用CIFAR-10 数据集验证AFL 算法在大规模和复杂图片分类场景的优越性。

1 深度基学习器

AFL 算法使用文献［19］所提及的VGG16 作为深度基学习器。所使用的VGG16 包括1 个输入层、13个卷积层、3 个全连接层、5 个最大池化层以及1 个输出层。同时，在VGG16 中，使用ReLU 函数作为激励函数来对每个卷积层的输出进行非线性的映射。其次，在输出层使用softmax 函数得到每个类别的概率分布。

另外，结合AFL 算法的横向联邦实现特点，添加了dropout 操作来随机删除若干个神经元，以提高基学习器的泛化能力。同时，对传统的VGG 训练过程的目标函数进行了更替，通过引入L2 正则化罚项来进一步提高基学习器的泛化能力。最终，AFL算法的目标函数如公式（1）所示，其中损失函数为交叉熵损失函数，m表示类别数，n代表样本数，yic表示样本i是否属于类别c，pic表示样本i属于类别c的预测概率，Ω为L2正则化罚项，λ为正则化系数。

2 融合Bi-HE的横向联邦学习模式

在传统的联邦学习中，一般使用的是单向加密的方式，即协调方负责生成密钥对，并分别把公钥发给参与方用于加密，但是此种加密方式下协调方可通过私钥得知参与方模型的明文信息，存在一定的隐私泄露的风险［20］。为保证参与方模型信息的隐私性，防止通过破解模型信息的手段反推出参与方的模型或数据特点，AFL 算法基于Paillier 同态加密算法，提出双向Paillier 同态加密机制——Bi-HE 机制。Bi-HE机制使用Paillier 同态加密算法为基算法的原因是Paillier同态加密可直接使用密文进行计算，且最终计算结果解密后与直接使用明文进行计算得到的结果一致，因此在计算过程中不需要多次进行加解密的操作，提高了联邦学习的效率［21］。

在Bi-HE机制中，参与方的明文信息依次使用协调方和参与方的公钥进行正向与反向加密。因此当AFL算法使用了Bi-HE机制后，算法中的参与方和协调方都只掌握密文信息的其中一把私钥，均无法通过自身携带的秘钥信息得到明文信息，有效保护了数据的隐私性。

2.1 Bi-HE机制

基于Paillier 同态加密算法提出的Bi-HE 机制生成正向和反向密钥对的方法的步骤如下：

步骤1协调方依据希尔伯特孪生素数猜想［22］产生2 个大素数对（x0，y0）和（x1，y1）用于生成正向和反向的密钥对，其中x0和y0、x1和y1均为满足公式（2）约束的孪生素数，其次公式（2）的gcd表示求2个数的最大公约数的函数。最后协调方将（x1，y1）发给参与方A用以生成反向密钥（详见步骤3），而（x0，y0）则由协调方保留并生成正向密钥（详见步骤2）。其中参与方A为众多参与方之一，本文选取第1 个加入到联邦学习系统的参与方作为参与方A，但是现实中可由各参与方商议后推举共同信任的其中一个参与方作为参与方A。

步骤2协调方随机选择一对满足公式（3）与公式（4）的整数g0和λ0，其中n0=x0·y0，gcd 和公式（2）一样表示求2 个数的最大公约数的函数。然后协调方依据n0、g0、λ0以及公式（5）得到正向密钥对K0=（P0，S0），其中P0=（n0，g0）、S0=（λ0，μ0）。

步骤3参与方A在接收到协调方发来的孪生素数对（x1，y1）后也随机选择一对满足公式（3）与公式（4）的整数g1和λ1，然后和协调方一样依据n1=x1·y1、g1、λ1以及公式（5）得到反向密钥对K1=（P1，S1），其中P1=（n1，g1）、S1=（λ1，μ1）。最后参与方A将反向密钥对广播给其他参与方。

2.2 融合Bi-HE机制的横向联邦学习过程

在协调方与参与方分别拥有了正向和反向密钥对后便可进行本文提出的融合Bi-HE 机制的横向联邦学习过程。其中融合Bi-HE 机制的横向联邦学习模式架构如图1所示，主要包括以下步骤：

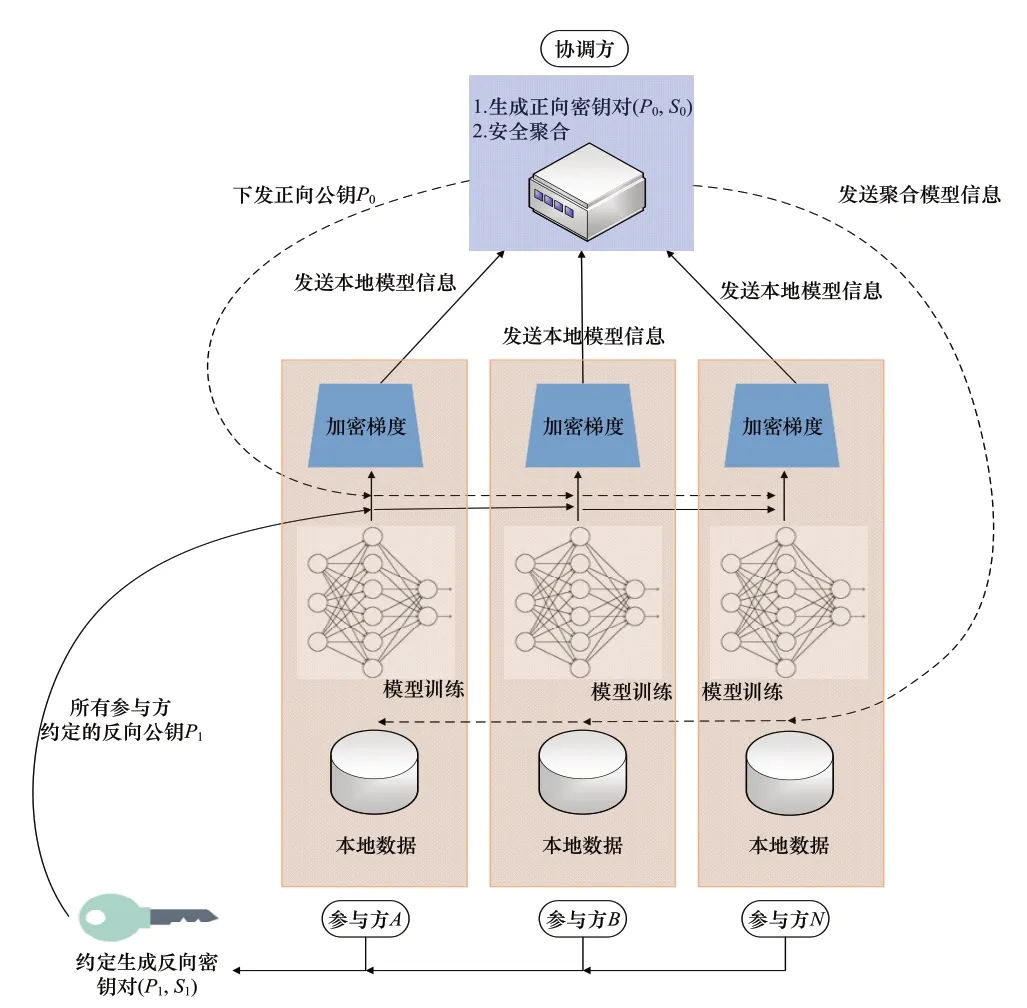
图1 AFL算法的横向联邦学习架构图

步骤1协调方下发VGG16模型结构给参与方，统一本次联邦学习所使用的统一模型的结构。

步骤2参与方用本地数据训练本地VGG16模型。

步骤3参与方将本次迭代得到的模型梯度G经由正向密钥对P0进行正向加密后，再使用反向密钥对P1进行反向加密，得到密文信息C（P1，C（P0，G）），并将其发给协调方。此情况下，参与方只拥有S0而缺乏S1，无法推算出其他参与方的梯度信息。

步骤4依据公式（6），协调方对参与方的加密梯度信息进行同态加权平均，得到聚合加密梯度c′G，其中cGi表示第i个参与方的VGG16模型的加密梯度，n表示参与方个数。因为协调方只拥有S1而缺乏S0，所以无法得到各参与方的明文梯度信息。

步骤5协调方将聚合加密梯度信息发给参与方，参与方利用聚合加密梯度信息更新本地模型。

重复步骤2~步骤5，直至达到最大迭代次数或模型收敛或达到early stopping条件为止。

3 自适应的模型聚合等待策略

在传统的横向联邦学习中，协调方需要等待所有参与方的本地模型信息返回后才会进行安全聚合。此策略下，如遇到通信阻滞情况，协调方将会进入无限的等待过程，缺乏对突发情况的自适应能力，严重影响联邦学习的效率。因此，AFL算法提出一种自适应的模型聚合等待策略。图2 为该策略的流程图，主要包括4个步骤。

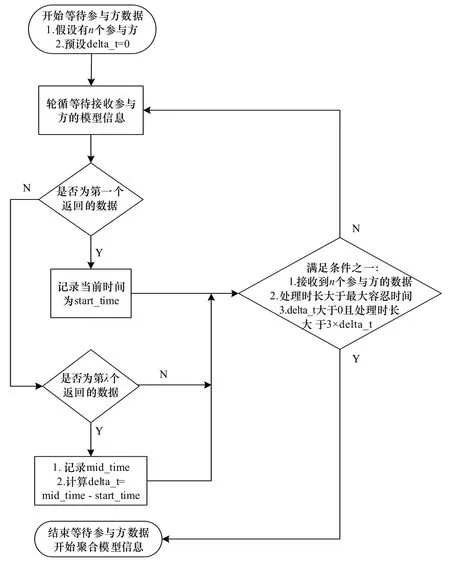
图2 自适应的模型聚合等待策略流程图

步骤1学习开始前，设定“每轮等待接收参与方模型信息的最大容忍时间”。

步骤2当协调方发出上一轮的模型聚合信息后，会进入轮循状态，监听最新的来自参与方的本地模型信息，并初始化delta_t为0。

步骤3当协调方收到第1份来自参与方的模型信息，记录当前轮的接收开始时间，记为start_time。而当协调方收到第份来自参与方的模型信息（记为λ），记录当前时间，记为mid_time，使用公式（7）更新delta_t：

步骤4协调方每隔1 min询问是否继续等待接受参与方的模型信息，满足以下条件之一则停止等待，利用已收到的模型信息进行安全聚合：

1）接收到所有参与方的模型信息数据；

2）当前的处理总时长大于最大容忍时间；

3）delta_t>0且当前的处理总时长大于3×delta_t。

4 实验与分析

4.1 实验环境与数据

4.1.1 实验环境

为验证AFL 算法的优越性，本文模拟一个包括1个协调方以及10 个参与方的横向联邦学习系统，并且使用AFL 算法的基学习器（传统的VGG16）、同样使用VGG16 作为基学习器且和AFL 算法具有一样联邦系统结构的传统横向联邦学习算法（HFL 算法）以及目前比较主流的深度卷积神经网络DenseNet 作为对比算法，在CIFAR-10数据集上进行对比实验。

4.1.2 实验数据

实验使用的数据是公开的图片分类场景的CIFAR-10数据集。CIFAR-10数据集是由Krizhevsky和Sutskever 整理的一个具有10 种类别的彩色图片集，该数据集中一共有5万张训练图和1万张测试图。由于横向联邦学习的数据特点是参与方之间的数据空间差异较大而特征空间差异较小，所以为模拟横向联邦学习的数据场景，需要将CIFAR-10 数据集划分出多个非独立同分布（non-IID）的子数据集，并将子数据集分别发给各参与方。因此，参照2021 年AAAI会议论文文献［23］对CIFAR-10数据集做以下处理：

设定一个取值为0.7 的non-IID 程度化因子q，并以q的概率将第i类别的数据分配给第i个参与方，并以（1-q）/9 的概率将其分配给其余9 个参与方，如此便可使每个参与方的本地数据集中具有某个标签的图片数据占多数，从而使得参与方之间特征空间类似而数据空间差异较大，实现横向联邦学习的数据场景的模拟。同时对每个参与方的本地数据集按照3：1的比例划分出训练集和参与方的“本地测试集”。所有参与方的本地测试集组成一个“多方测试集”。

4.2 实验结果与分析

图3 示出了各算法在各参与方的本地测试集的平均测试准确率。其中AFL 算法的曲线代表横向联邦模型在各参与方的本地测试集的平均准确率；而VGG16 和DenseNet 的曲线代表各参与方的本地模型在各自的本地测试集的平均准确率，类似于集中式学习模式。可以看出，随着迭代次数的增长，当模型接近稳定后，AFL 算法和传统VGG16 的准确率相当，而DenseNet 的准确率略高。这说明AFL 算法中提出的针对VGG16 的横向联邦实现方式所产生的模型性能损耗是可接受的，但在集中式学习场景下性能差于DenseNet。

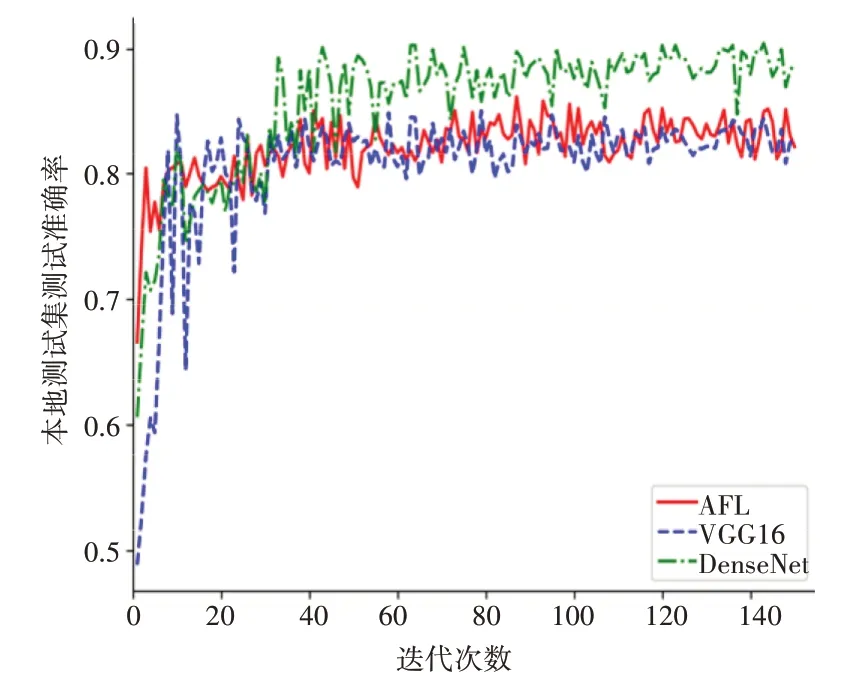
图3 各算法的本地测试准确率

然而，结合图4 所示的各算法在多方测试集的测试准确率的表现却可以看出，传统的集中式学习算法的准确率相对于联邦学习来说有着较大的差距，同时在与自身在本地测试集的表现相比也有较大幅度的性能降低。因此，综合图3 以及图4 的实验结果可以说明：在需要实现各方隐私保护的场景下，因为参与方的本地模型的学习被局限在自身数据集上，所以无法习得其他参与方的数据知识，仅能对自己所拥有的场景数据进行特征学习，而对其他场景数据缺乏泛化能力。而在AFL算法中，由于参与方在横向联邦学习过程中通过协调方的聚合模型信息间接获得了其他参与方的知识，这种“数据不动，模型动”的知识交换方式使得AFL 算法在大规模和复杂的图片分类场景下展现出了较好的泛化能力。

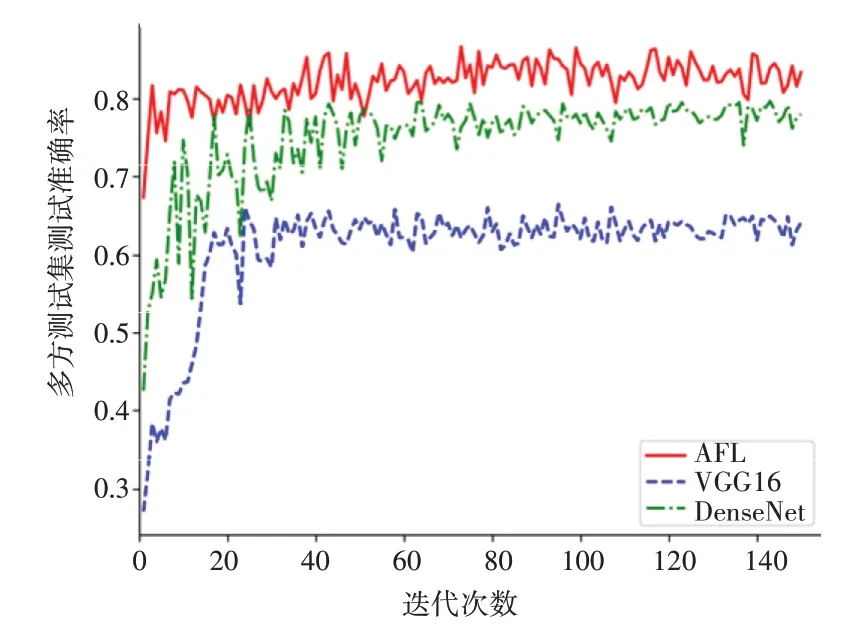
图4 各算法的多方测试集准确率对比

其次，为说明在通信阻滞的场景下，AFL 算法所提出的自适应的模型聚合等待策略的有效性，每轮迭代随机抽取2 个参与方进行如下处理以模拟通信阻滞的场景：当参与方完成本地模型的更新后，休眠3 min 再将模型信息发给协调方聚合。从图5 可以看出，同样使用VGG16 作为基学习器且和AFL 算法具有一样联邦系统结构的HFL 算法因为协调方需要等待所有参与方的模型信息的返回，而AFL算法所使用的自适应的模型聚合等待策略会依据delta_t 来动态更改最大等待时长，所以在通信阻滞的情况下，AFL算法的学习效率高于传统的横向联邦学习模式，具有一定的自适应和通信阻滞应对能力。

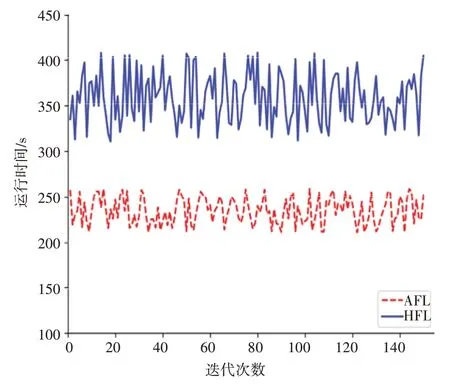
图5 AFL和传统HFL的多方测试集测试准确率

最后，图6展示出了AFL 算法和HFL 算法的多方测试集的准确率对比。可以看出虽然自适应的模型聚合等待策略使得协调方在每次迭代中都有可能会抛弃若干个训练超时的参与方的模型信息，但是当抛弃的参与方的比例较低时，此操作所导致的准确率误差是可接受的。换言之，在大规模和复杂的图片分类场景下，随着参与方的增加，此种效果换效率的方式是存在可行性的。

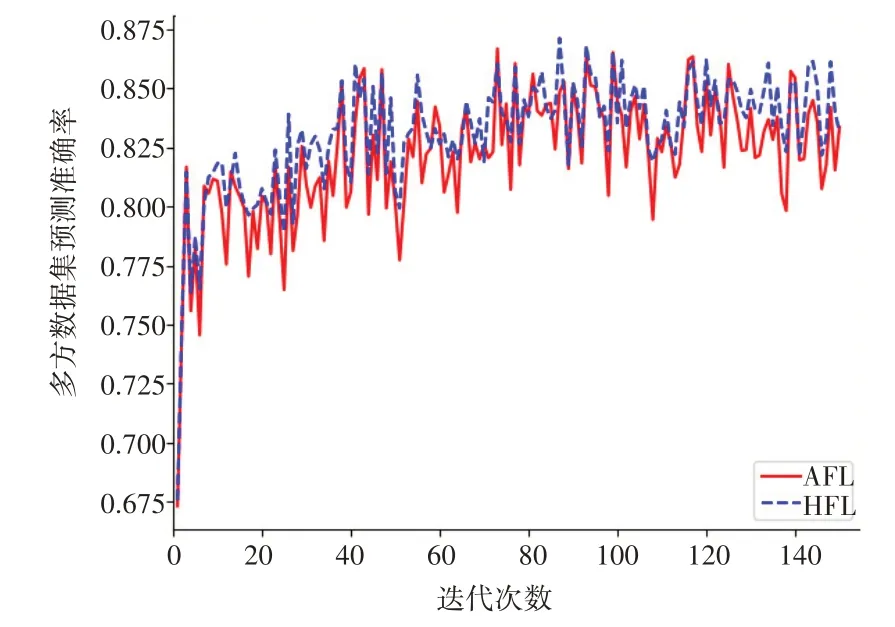
图6 AFL和传统联邦学习的学习时长对比

综上可得，在大规模和复杂的图片分类场景下，AFL算法能有效解决隐私保护和数据孤岛问题，并且具有更好的泛化能力。同时，相对于传统横向联邦学习模式，AFL算法具有更好的自适应能力和通信阻滞应对能力。整体而言，AFL算法在大规模和复杂的图片分类场景下具有一定的优越性。

5 结束语

为解决隐私保护和数据孤岛的问题，本文提出了一种基于双向同态加密的深度联邦图片分类方法——AFL 算法。AFL 算法解决了集中式学习的隐私保护问题，同时也解决了分布式现场学习的数据孤岛问题。其次，AFL 算法基于Paillier 同态加密算法提出一种双向的Paillier 同态加密机制——Bi-HE 机制。相比于传统联邦学习中的单向加密，融合Bi-HE机制的AFL 算法能避免协调方得到参与方的明文模型信息，进一步加强了对隐私数据的保护。同时，AFL 算法优化了传统的联邦学习的模型聚合等待过程，提出了一种自适应的模型聚合等待策略，避免了协调方无限等待参与方的情况，提高了在通信阻滞情况下联邦学习的效率。最后，使用CIFAR-10 的对比实验结果表明，在大规模和复杂的图片分类场景下，AFL 算法能在参与方不交换原始图片数据的前提下习得所有参与方的知识，同时具有更好的自适应能力和通信阻滞应对能力，具有一定的优越性和可行性。

然而，AFL 算法作为联邦学习的实现案例，也面临着联邦学习的共同挑战，需要学者们进行更深入的研究［24-26］，比如：

1）如何能够吸引更多的参与方自愿加入联邦学习中，如何建立和完善一套公平的激励体制。

2）如何在联邦学习系统中识别出恶意的参与方，防止其传输负面的模型更新信息，保证系统的安全与性能。

3）如何在参与方与协调方之间建立一个可靠且高效的通信环境。

4）如何让联邦学习系统兼容更多的机器学习算法，完成更多机器学习算法的联邦实现。

5）如何提出一种更快速且更有效的协调方聚合方法。

6）随着攻击手段的发展，隐私保护面临着巨大的挑战，一个方案往往无法堵住所有的攻击漏洞。同时随着量子物理的发展，量子密码学也许会成为未来的重要研究方向之一。