物理化学课程中热力学基本公式识记技巧

庾弘朗

（韩山师范学院 化学与环境工程学院，广东 潮州 521041）

化学热力学［1］研究化学反应以及系统状态之间热和功的转换关系，从而实现对化学反应方向和程度做出准确判断，因此在大学化学中占有重要地位.准确理解并全面掌握热力学特性函数与特征变量之间的对应关系、化学热力学四个基本方程以及Maxwell 公式是化学热力学教学重点与难点之一.因化学热力学所涉公式繁多［2-5］、函数之间相互关联，规律隐性，容易混淆出错，故持久正确识记热力学相关公式或函数关联关系存在较大困难与障碍.在布鲁姆认知目标中，识记是认知的开端，识记与保持是再认和再现的前提与基础.识记成败深刻影响后续认知目标的达成.那么，对于热力学基本公式，除数理推导识记方法之外，如何创新教法并选用合适记忆方法，帮助学生实现轻松精准记忆，巩固学习效果呢？迄今为止已有推理法［1，5-7］、图形法［2-8］、方程式记忆法［5］、比较记忆法［6］、坐标记忆法［4，8］等记忆方法的报道.在此，笔者根据多年讲授物理化学课程经验，以热力学基本公式与函数关系为例，分享一些不同以往报道的记忆技巧.实践表明这些技巧能有效提高记忆的主动性与趣味性，促进对知识的加工与内化，增强记忆准确性，巩固学习效果.

1 特性函数与特征变量对应关系——故事记忆法

对于单组分封闭系统，若热力学函数仅与系统状态有关，系统状态一定，状态函数具有确定值.若系统状态改变，状态函数值也随之改变，这样的函数被称为热力学状态函数［1］.状态函数的变化值仅与始态和终态有关，而与所经历的过程途径无关.单组分封闭系统热力学常用八个热力学状态函数，分别为热力学温度T，压强P，体积V，熵S，内能U，焓H，亥姆霍兹自由能A以及吉布斯自由能G.其中U、A、G与H四个状态函数本身具有能量量纲，另外P、V以及T、S之乘积，即PV、TS也具有能量量纲.

根据Gibbs 相律，定组成均相封闭系统只有两个自由度.八个状态函数中任一状态函数均可由其它两个独立的状态函数来确定.例如，因变量U可用T，P，V，H，A，G，S中任意两个作为自变量来表达.Massieu 于1869年指出，对于U，H，S，A，G等热力学函数，只要其独立变量选择恰当，就可以从一个已知的热力学函数，通过偏微商求得其他热力学函数，从而可以把一个均匀系统的平衡性质完全确定下来.这个已知的热力学函数就称为特性函数，所选择的独立变量就称为该特性函数的特征变量.通常为了简化运算，约定俗成选S，V作为特性函数U的特征变量，选S，P作为特性函数H的特征变量，选T，V作为特性函数A的特征变量，而选T，P作为特性函数G 的特征变量.特性函数与相应特征变量函数关系分别简记为：U=U(S,V)、H=H(S,P)、A=A(T,V)与G=G(T,P).

热力学能U、亥姆霍兹自由能A、吉布斯自由能G与焓H等热力学特性函数都有各自的独立变量.精准牢记各自的对应关系，对后续正确记忆与理解四个热力学基本公式和麦克斯韦关系式非常重要.为让学生轻松且长久记牢每个特性函数与相应特征变量，编了一个故事：亚洲电视台（ATV：Asia Television）邀请美国志愿者（USV：United States Volunteers）探讨了三磷酸鸟苷（GTP：Guanosine triphosphate）与健康微笑和平（HSP：Health Smile Peace）主题.学生只要想起亚洲电视台（ATV），自然容易记住亥姆霍兹自由能A是特征变量T、V的特性函数，记为：A=A(T,V).同样，U是特征变量S、V的特性函数，记为：U=U(S,V)；H是特征变量S、P的特性函数记为：H=H(S,P)；而G是特征变量T、P的特性函数，记为：G=G(T,P).特性函数、特征变量与故事中字母缩写对应关系见式（1）～式（4）.

运用这种编故事的教学方法，激发了学习兴趣，较好地把热力学特性函数与相应的独立变量巧妙地关联起来，使得记忆其对应关系轻松容易，明显地加强了记忆效果.

2 四个热力学基本方程——规律记忆法与口诀记忆法

热力学基本公式就是前述8 个热力学函数间的关系式.对于单组分均相封闭系统，热力学第一定律与第二定律分别引出热力学能函数U与熵函数S，而热力学第一、第二定律联合公式①dU=TdS-PdV则把U和S定量关联起来.这就是热力学第一个基本方程.再根据H，A、G定义及其全微分性质，可以轻松导出其余三个热力学基本方程：②dH=TdS+VdP、③dA= -SdT-PdV与④dG=-SdT+VdP，具体推导过程参见教材［1］.这种推导法是教材上和教学过程中，介绍如何获得四个基本方程的最普遍方法.虽然整个推导过程难度不大，四个方程形式与内容并不复杂.但教学过后，时间稍长，通过默写检查，结果表明大多数学生对这四个方程的记忆基本上都是失败的.如何在教学之后让学生记牢记准呢？下面是强化记忆的教学方法.推导之后，让学生观察四个方程的特征并引导其总结为：第一，等号左边分别为U、H、A与G函数的全微分表示dU、dH、dA与dG，等号右边都是两个微分项的代数和；第二，右边微分项中微分的两个变量就是左边特性函数的特征变量；第三，各方程的微分项，T只与S组合，P只与V组合，只有这样组合的才具有能量量纲；第四，正负号规则，当T、V为不变量时为正号，当P、S 为不变量时取负号.为了方便记忆，将正负符号口诀归纳为：正直的电台TV 批死PS 负面的人.运用规律记忆法、口诀记忆法教学，促进学生对知识的特点和规律进行观察、加工与内化，即使不推导，学生亦可实现轻松牢记默写出（5）～（8）四个方程，提高记忆的准确性与持久性.

3 特性函数间关系以及麦克斯韦关系式——正方形图形记忆法

对于特性函数间关系以及麦克斯韦关系式，则采用正方形图形记忆法.具体方法是，作正方形，如图1.具有能量量纲的G、A、U与H函数依次为正方形四边.选择其相应独立变量P、T、V、S依次为正方形的四个顶点.对角线顶点T对S，P对V，则对角线代表函数乘积TS、PV，也具有能量的量纲.任意三个顶点构成的三角形中，三边代表的函数值具有和差关系.符号规则：对角线T乘以S、V乘以P取正号，若次序相反（S乘以T、P乘以V）则取负号.例如三角形124中，按顶点1→2→4 次序，边12=边24+对角线VP，由于V乘以P，故取正号，即G=A+PV；同样，在三角形213中，G=H+（-ST）=H-ST；在三角形134 中，H=U+VP；在三角形342 中，U=A+TS，而在三角形421中，A=G+(-PV).教学中，利用这种图形记忆法，形象具体地呈现了八个热力学函数之间的独特的“三边和差”关系，因而助益学生轻松牢记8个热力学状态函数的相互关系式（9）至（12）.

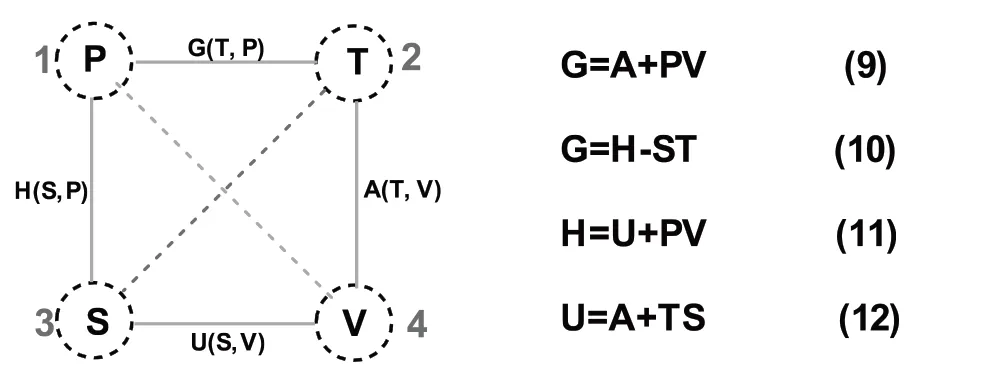
图1 八个热力学函数的正方形分布图

基于热力学四个基本方程，容易推导出简单系统的非能量热力学函数（S，V，T，P）之间的偏微分关系式［1］，即获四个Maxwell公式，如下列（13）～（16）式所示.

4 结论

经过多年实践摸索与教学反思，以物理化学课程中单组分封闭系统的热力学方程与函数关系为例，提出简单快捷的故事记忆法、规律记忆法、口诀记忆法、正方形图形记忆法.这些方法可以提高记忆主动性与趣味性，增强记忆效率，巩固学习成果.这些方法关键是牢记特性函数与其独立变量对应关系、理清相应方程的规律和画对八个热力学函数的正方形分布图.众所周知，教学有法，但无定法，贵在得法.唯有创新教法，并在实践中迭代优化，才能不断提高教学质量.