基于改进麻雀搜索算法的爆破参数优化①

闫祎然， 徐振洋， 刘 鑫， 王雪松， 张宇庭

（1.辽宁科技大学 矿业工程学院，辽宁 鞍山 114051； 2.沈阳工业大学 建筑与土木工程学院，辽宁 沈阳 110870）

爆破参数不仅直接影响爆破成本和爆破质量，还会间接影响钻孔、铲装、运输等环节的生产成本。 采场生产过程中，必须寻求最优的爆破参数，以便获得较好的爆破质量以及较低的采场生产成本。 随着计算机技术飞速发展，近年来参数的优化选取逐渐与人工智能相结合［1-5］，本文利用萤火虫算法优化麻雀搜索算法，提高其搜索能力和求解精度，并能迅速地查找出最优值。 本文以西藏玉龙矿业为例，分析矿山采场成本影响因素，构建采场生产成本模型，利用改进的麻雀搜索算法求解模型，得到最优成本下的爆破参数。 实践证明，萤火虫算法可以有效提高麻雀搜索算法的寻优效率，可为台阶爆破参数选取提供新途径。

1 露天矿台阶爆破参数优化模型

通过优化爆破参数，可以有效改善矿山露天开采工程爆破效果、减少炸药单耗量，进而降低爆破成本。爆破效果的优劣程度一般用矿岩的平均块度和大块率来衡量。 为提高矿山经济效益，控制生产成本是目前研究的重要课题之一［6］。 近年来，许多研究者将岩石块度与生产成本联系起来，建立了成本优化模型［7-8］。

根据矿山生产管理模式，钻孔作业成本以每米钻进成本为单位计算，与钻孔工作量以及孔网参数有着直接关系，因此，钻孔成本计算函数关系式为：

式中Cz为钻孔成本；e1为钻进每米消耗成本；L为钻孔深度；H为台阶高度；S为炮孔担负面积；γ为矿石容重。

露天矿爆破成本主要是台阶爆破成本，它主要体现在爆破器材与炸药消耗两个方面，而这与爆破参数的选择密切相关：

式中Cb为爆破成本；q为炸药单耗；e2为炸药单价；e3为爆破器材消耗单价。

露天矿主要以挖掘机、电铲等设备进行铲装作业，主要成本在于设备的能源消耗，可通过统计设备的电耗与油耗获得：

式中Cc为铲装成本；X为矿石的平均块度；f1、f2均为函数模型的相关系数。

露天矿矿石多采用汽车运输，主要成本在于汽车的能源消耗，可通过统计汽车的电耗与油耗获得：

式中Cy为运输成本；f3、f4、f5均为函数模型的相关系数；e4为每吨矿石的运输成本。

本次模型的构建以西藏玉龙矿业为背景，该矿山位于高原地区，矿山作业受该地区特殊环境的限制，生产成本相对较高。 针对矿山的实际生产状况，提出了采用低成本、高效的台阶爆破方法。 但由于露天爆破成本受到多种因素的影响，如在爆破后，矿岩块度的具体分布情况将直接影响并决定其爆破成本。 最终，建立的露天爆破成本控制数学模型为：

式中C为露天采场生产成本；Cp为排岩成本。 以上参数单位均为元／t。 由于忽略了管理成本，Cy＝Cp。

2 采场生产成本模型求解算法

2.1 麻雀搜索算法

麻雀搜索算法（SSA）是根据麻雀的群体觅食行为提出的一种群智能算法［9］，该算法将样本看作一个麻雀群体，将群体按职能分为发现、加入和警戒3 种身份类型的成员，通过调整3 种成员所占比例来决定麻雀群体的搜索能力和收敛速度，最终经过多次迭代完成整个函数的寻优。 该算法能较好地解决单峰、多峰函数的寻优问题，且具有较好的收敛性和精确性，但其寻优能力较为薄弱。

通常情况下，一个群体中所有麻雀都可以用一个数据集合来描述，设该群体中有n只麻雀，那么该群体可被表示为：

式中d为待优化变量的维度；n为麻雀数量。

则所有麻雀的适应度值可表示为：

式中f为适应度值。

发现者在算法中被赋予了较高的适应度值，因此，在整个种群搜索过程中以发现者的目标作为整个算法的寻优目标，并且发现者会被赋予更多新的食物以提高其搜索能力及范围，发现者位置变换如下：

式中p为目前迭代次数；T为最大迭代次数；α一般为（0，1］中的数值；Q为服从正态分布的随机数；L表示一个1×d的矩阵，该矩阵内所有元素均为1。

按照麻雀的行为准则，加入者的位置更新描述如下：

式中K为［－1，1］之间的某一数值；β为步长控制参数；e为较小实数；fi为第i个麻雀的适应度值；fg为最优适应度值；fw为最差适应度值。

2.2 萤火虫算法优化麻雀搜索算法

萤火虫算法（FA）是一种将函数值的改变与萤火虫的群体行为相结合的启发式算法［10］，利用个体的光亮程度来反映函数值的优劣。 该算法在局部搜索方面表现出了良好的性能，并通过干扰麻雀的位置，使其移动效率得到提高，局部寻优能力得到明显改善。

萤火虫的亮度函数为：

式中I0为初始的萤光强度，根据目标函数变化而变化；γ为光强度吸收系数，随着距离增大而减小；ri，j为萤火虫从i到j的空间距离。

萤火虫的吸引度为：

式中β0为r＝0 时的最大吸引度。

萤火虫i被吸引向萤火虫j移动的位置更新为：

式中xi与yi为萤火虫在当前种群中的位置；α为步长因子，一般为［0，1］中的数值；rand 为［0，1］中服从均匀分布的随机数。

该优化主要是在麻雀搜索过程中，通过萤火虫对麻雀种群内发现者的定位进行干扰，以增强其搜寻力，使其寻优目标更趋近于最优值目标，对麻雀与最优的麻雀通过萤火虫干扰方法进行定位更新，将干扰后的麻雀与干扰前的麻雀进行比较，如果干扰后的麻雀为最优，则可改变麻雀定位。 此算法提高了原麻雀算法对于单峰与多峰函数的优化能力。 改进算法流程如图1 所示。

图1 改进麻雀搜索算法求解流程

一般采用测试函数验证优化后算法的寻优能力。遵循公平原则，测试的两个算法选用相同的参数，麻雀种群大小为20，迭代次数为1 000 次，为减小偶然误差对实验结果的影响，测试函数共测试20 次，以获得目标函数的最优值，结果见图2。 通过图2 对比可知，原麻雀搜索算法最优值远逊色于改进后的麻雀搜索算法，说明改进麻雀搜索算法精度得到了大幅提升。

图2 适应度值曲线

本次仿真实验利用多峰值测试函数进行测试，该函数搜索维度为30 维，搜索范围为［－500，500］。 改进麻雀搜索算法运动轨迹见图3。 从图3 可以看出，改进麻雀搜索算法大多数能聚集到最优解附近，说明该算法具有较好的寻优收敛能力，能够快速地找到最优值，实现对函数快速、精确的求解。

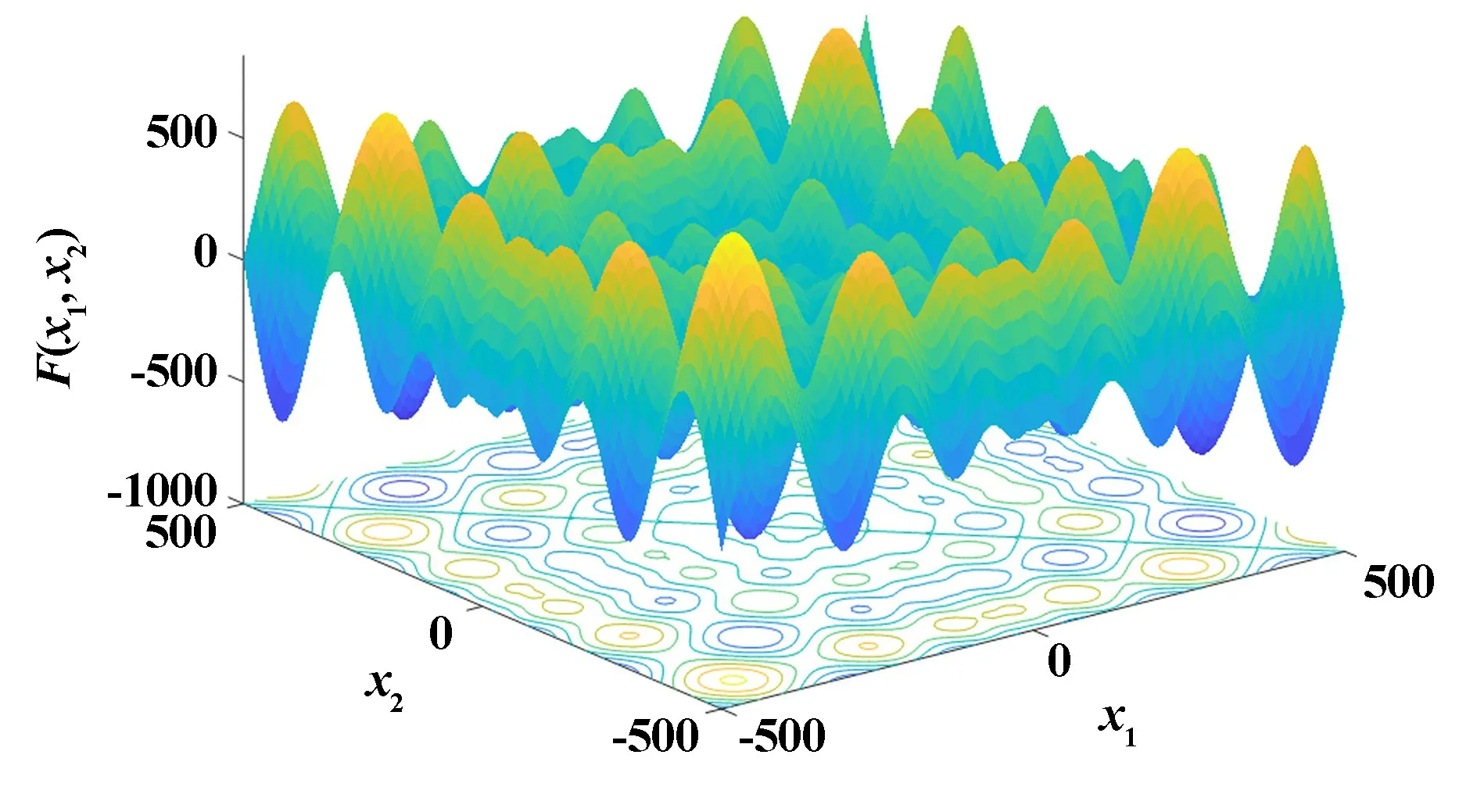
图3 改进麻雀搜索算法运动轨迹

3 台阶爆破参数优化

3.1 工程参数采集

西藏玉龙矿业地处高海拔的青藏高原，矿石赋存空间海拔标高一般在4 200 ～4 600 m 之间。 其含矿物岩石主要有长英质角岩、角岩化石英砂岩等，该矿山受高原地质环境、气候特性的影响，生产设备能耗相对较高，炸药与爆破器材等运输距离较远，导致该矿区生产成本相比于平原地区明显增多，亟须进行采场生产成本的控制。

通过采集该矿山实际生产数据得出，该矿山钻进成本e1＝44 元／m，爆破平台高度H＝15 m，炮孔直径d＝140 mm，最大孔深Lmax＝18.4 m，平均孔深L＝16.9 m，矿石容重γ＝2.96 t／m3，炸药以混装乳化炸药为主，单价e2＝5.9 元／kg，爆破器材消耗单价e3＝4.2 元／m，矿石运输成本e4＝4 元／t。 通过统计平均块度与铲装成本数据，计算得到f1＝0.013，f2＝0.18，通过统计平均块度与运输成本数据，计算得到f3＝－0.002 3，f4＝0.06，f5＝0.96。

将实际参数代入式（5）中，得到采场成本计算目标公式，采用改进的麻雀搜索算法，对目标函数进行了优化，得到参数模型公式为：

式中a为孔间距，m；b为排距，m；X为平均块度，cm；m为密集系数；W1为底盘抵抗线，m；Q为炸药量，kg；H为台阶高度，m。

根据以上经验公式可得炸药单耗推荐取值范围为［0.3，0.6］，孔间距推荐取值范围为［3.0，7.0］，排距推荐取值范围为［3.0，6.0］。 利用改进麻雀搜索算法对式（14）进行求解，最终得出最优生产成本为11.06 元／t，炸药单耗q＝0.32 kg／t，孔间距a＝6.243 2 m，排距b＝4.946 4 m。 参数均在合理的取值范围中，能够满足实际需求。

3.2 数学模型求解

为了验证改进麻雀搜索算法的寻优能力，在此模型的求解中，选取了目前应用比较成熟的差分进化算法（DE）、粒子群算法（PSO）和遗传算法（GA）进行比较［11-13］。 由于构建的求解爆破参数数学模型复杂度相对较低，设置每一种算法迭代次数为100 次，初始种群为20，空间维度为3。 4 种算法求解结果见图4。 从图4 可以看出，模型迭代求解过程中，所有算法均起到了优化效果，其中改进麻雀搜索算法适应度值更好，迭代次数约40 次时基本达到最优，其他3 种算法在迭代约20 次时达到最大值。

图4 4 种算法求解结果

3.3 现场试验

通过分析，确定西藏玉龙矿山在实际爆破应用中的最优孔网参数为：孔间距a＝6.2 m，排距b＝4.9 m。经现场应用试验验证，采用优化后的爆破参数能够有效降低爆破中大块率高、缩口严重的问题，大块率控制在10%以内，提高爆破效果的同时采场成本降低了7.5%。

4 结 论

1） 在现有采场生产成本模型基础上，通过将排岩成本量化为影响采场生产成本模型的因素，优化了露天矿山成本控制模型，提高了矿山成本控制精度。

2） 优化了采场成本模型的求解算法，利用测试函数证明了算法的优越性，结果表明，改进麻雀搜索算法在收敛速率上差异不大，在求解精确度上显著优于原始麻雀搜索算法。

3） 将该方法成功应用于矿山实际中，通过算法求解得出西藏玉龙矿业最优成本下的爆破参数为：孔间距a＝6.2 m、排距b＝4.9 m、炸药单耗q＝0.32 kg／t，该条件下生产成本11.06 元／t。 研究成果可为具有相似工艺的矿山提供借鉴。