基于连续介质损伤力学的坑蚀高强钢丝疲劳寿命预测

卢泽坤，张军,毛江鸿，郑荣国，吴军武

(1.重庆交通大学土木工程学院，重庆 400074；2.浙大宁波理工学院土木建筑工程学院，浙江 宁波 315100；3.四川大学建筑与环境学院，四川 成都 610065；4.浙江金温铁道开发有限公司，浙江 温州 325041)

0 引言

大量悬索桥和斜拉桥其拉索吊杆服役期间，在腐蚀环境和疲劳荷载的共同作用下内部钢丝出现严重的锈蚀损伤，其疲劳损伤直接影响整个桥梁结构体系安全[1]。国内外的实地工程调研表明，大跨度桥梁事故大多是由拉索内部高强钢丝的腐蚀产生的蚀坑导致疲劳寿命急剧衰减造成的[2]。可见，高强钢丝的腐蚀与疲劳特性评估对于桥梁的安全运营具有重要意义。

构件疲劳性能研究存在多种方法，传统基于试验的S-N 曲线法依赖大量试验数据进行公式拟合，只关注材料疲劳寿命而忽略了疲劳损伤的非线性发展[3]。断裂力学方法则聚焦单一宏观裂纹的扩展规律，无法考虑钢丝疲劳损伤过程中的应力应变演化进程[4]。连续介质损伤力学的方法将构件看作连续的整体，通过定义损伤变量来研究循环荷载下构件的损伤以及力学性能退化规律[5]。基于CDM 方法研究材料损伤演化以及疲劳寿命分析已有大量文献，如W.P.Hu等[6]基于连续介质损伤力学建立了与腐蚀疲劳的损伤演化方程，预测了2024-T62 铝合金在盐雾中的腐蚀疲劳寿命，预测结果与试验数据较符合。Zhang T 等[7]采用三维有限元法将CDM多轴损伤应用于钛合金中，验证了微动疲劳研究中的有效性。张昉等[8]进行了疲劳试验，对CDM 模型进行参数标定，并通过ABAQUS 的二次开发平台UMAT 实现了坑蚀钢筋的疲劳寿命预测，发现疲劳寿命预测与试验结果吻合良好。上述研究表明CDM 法对于循环荷载下含有损伤的材料疲劳寿命预测具有良好的适用性，但鲜有文献将CDM 模型应用于坑蚀高强钢丝的疲劳寿命预测。

本文通过6 根无锈蚀钢丝疲劳试验标定了CDM 模型参数，利用ABAQUS的二次开发平台UMAT 编写钢丝材料本构程序，通过电化学加速锈蚀获取了25 根具有不同坑蚀尺寸的钢丝，并进行单向拉伸疲劳试验，用于验证模型的疲劳寿命预测。

1 连续介质损伤力学模型

在损伤力学中利用等效性假设，认为损伤材料本构关系与无损状态下的本构关系形式相同，在循环荷载作用下，材料的力学性能劣化表现为刚度的下降，定义损伤变量D为[5]：

式中，E为无损伤材料的弹性模量；ED为含有损伤的等效弹性模量。

根据应变等原理，弹性范围内的损伤材料可采用无损材料的本构关系表达，其关系式为：

式中，ν是材料的泊松比；σkk是第一应力不变量；δij是Kronecker 符号；σij和εij分别是应力张量和应变张量。

疲劳损伤过程的描述需要给出D的演化方程。关于弹性条件下多轴应力状态的疲劳损伤演化，Chaudonneret 等[9]提出了疲劳损伤演化模型，其表达式为：

式中，N是循环次数；β、M0和b2是无量纲材料常数；AII是八面体剪应力的幅值；ΣH,mean是平均静水应力；，其中，

式中，Sij,max和Sij,min分别为一个疲劳荷载循环中偏应力张量分量的最大值和最小值。

式中，σu是极限抗拉强度；Δσ是应力比为-1 的疲劳强度；a和b1是无量纲材料常数；σeq,max是一次疲劳荷载循环中Mises 等效应力的最大值；运算符“〈＞”的定义为若x〈0，则〈x＞=0；若x＞0，则〈x＞=x。

2 疲劳试验

2.1 模型参数标定疲劳试验

为获取材料模型参数开展了材料参数标定试验，本文的疲劳试验均按照《桥梁缆索用热镀锌或锌铝合金钢丝》（GB/T 17101-2019）[10]规定方法进行疲劳加载。采用25t 电液伺服疲劳试验机进行正弦波常幅疲劳加载，夹持端包裹铝片以避免试件在夹持部位首先断裂，加载频率为5Hz。本文所用材料为柳州市桥夏缆索制品有限公司提供的PES7-109ZZL 拉索中取出的φ7mm 镀锌钢丝，试件长度取为300mm，主要的化学成分和基本力学性能分别如表1 和表2所示，标定参数疲劳试验结果如表3 所示。

表1 高强钢丝主要化学成分

表2 高强钢丝基本力学性能

表3 参数标定疲劳试验结果

2.2 坑蚀钢丝高周疲劳试验

为了验证模型的有效性，开展坑蚀钢丝的疲劳试验。试件蚀坑采用外加电流加速锈蚀的方法制作，如图1 所示。首先，在试件表面缠绕防水绝缘胶带且两端用硅酮胶密封，在中间位置暴露5mm×4mm(l×w)的椭圆形待锈区，按目标蚀坑深度分为5组，每组5个试件。然后，将试件放入质量分数为5%的NaCl溶液中，直流电源正极接试件，负极接不锈钢片，电压恒定为15V。最后，通过法拉第定律和实测蚀坑深度确定通电时间。各组试件的锈蚀尺寸如表4 所示，编号中的下标为目标锈蚀深度。

表4 钢丝试件蚀坑尺寸表

图1 加速通电锈蚀

试件各组CF1-5 试件的峰值应力分 别 设 置 为 700MPa、780MPa、870MPa、960MPa、1050MPa，应力比均为0.5。试件疲劳加载和断裂试件如图2所示，疲劳加载参数及寿命如表3所示。

图2 疲劳加载及断裂试件

3 有限元模拟

3.1 材料参数标定

在损伤本构关系中，极限抗拉强度取值（如表2 所示）σu=1750，杨氏模量E取200000MPa，泊松比ν为0.3。根据Basquin 公式[11]计算应力比R=-1 情况下钢丝的疲劳极限σn。Basquin 公式的对数形式为：

式中，Δσ是应力幅值；A和B是无量纲材料参数。

将F10～F40组的数据以对数坐标进行线性拟合，得lgNf=-2.95lgΔσ+12.69。取应力循环基数为2×106次，即可得到σn=146MPa。在疲劳损伤演化方程中，有β、M0、a、b1和b2共5 个参数待标定。将弹性损伤演化方程式（3）以单轴应力形式积分，得到试件在常幅疲劳荷载作用下的疲劳寿命表达式为：

首先，代入表3 中F10-F40的数据，可消去未知数b1和b2，求解出参数aM0-β的值。再将F50和F60的数据代入，可求解出参数b1和b2的值，最后，采用Zhang T 等[7]提出的数值求解方法获得参数a的值。所得参数值如表5所示。

表5 高强钢丝疲劳损伤演化模型参数取值

3.2 材料子程序算法

采用数值求解实现本文上述模型，本文基于ABAQUS 软件的UMAT 二次开发模块，使用Fortran 语言定义材料属性并用于有限元分析。算法流程图如图3所示。

图3 算法流程图

①初始化材料参数。将初始损伤和初始等效塑性应变设置为0。

②计算该循环下各积分点的应力历程。

③计算损伤值并更新循环次数。

④判断该循环下个积分点是否有损伤值D≥1，是，则结束程序，并输出疲劳寿命；否，则返回步骤②，代入新的损伤变量并更新弹性模量进入下一个循环，直到出现积分点损伤值D≥1。

3.3 有限元模型

根据试验试件建立有限元模型，通过在圆柱体上应用布朗运输减去椭圆形蚀坑建立坑蚀钢丝模型。单元类型采用八节点六面体实体单元（C3D8），由于蚀坑部位的复杂受力，为提高其计算的精确性在蚀坑位置进行网格精细化处理。材料属性调用上述的UMAT 子程序。在第一个分析步加载对应轴向均布荷载，应力比为0.5 的循环应力，时间增量步设置为200，每个增量步代表一次循环计算，每一次循环计算对应的疲劳寿命通过子程序中的dN定义，定义每一次循环计算疲劳寿命为1 万次。本文后续模型的建立均采取该方法。

4 模拟结果分析

采用上述有限元模型建立的模型对坑蚀试件进行了疲劳寿命预测，为了验证该方法的有效性，对文献[12-13]的坑蚀钢丝疲劳寿命进行了数值模拟，预测结果如图4 所示。图中实线表示预测值与试验值相同，虚线是误差范围为±20%的置信区间。由图可知通过CDM 模型预测值与试验值之间的误差基本在20%以内，个别数据点偏离较大，其原因可能是各文献钢丝锈蚀方式或疲劳试验应力比的设置差异导致。上述结果说明基于CDM 方法预测的不同蚀坑尺寸和不同应力幅的坑蚀钢丝疲劳寿命结果较好。

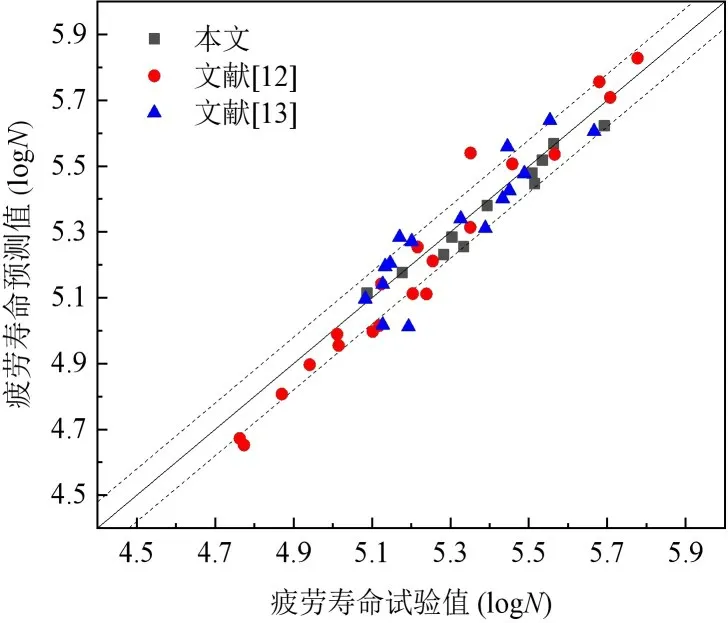
图4 疲劳寿命预测值与试验值对比图

5 结论

本文基于ABAQUS 平台的UMAT子程序引入连续介质损伤力学，建立了坑蚀钢丝预测模型，预测了坑蚀钢丝疲劳寿命，主要结论如下。

①基于ABAQUS 的二次开发平台UMAT建立了CDM 模型，对于不同蚀坑尺寸和不同应力幅的坑蚀钢丝疲劳寿命预测具有较好的结果，疲劳寿命预测值与实验值误差在±20%以内。

②考虑材料损伤演化发展直到破坏的理论基础所建立的CDM 模型，对于不同蚀坑尺寸的坑蚀钢丝疲劳寿命预测分析具有良好的适用性。