耐环境机械臂的仿真模型与轨迹规划研究

孔德凯，谭辉，张丽华，任德彬，张媛媛，段绪章

（西北机电工程研究所，咸阳 712099）

引言

随着对军用产品和民用产品的质量要求不断提高，气候环境试验过程考核也更加全面。高低温、低气压等试验在产品可靠性验证类目中较为常见。而在部分实验运行过程中，通常无法打开试验箱门对被试样品进行手动操控，造成试验样品欠试验。机械臂作为工业自动化的标志应用在各个领域[1]，本文将设计一种可实现对被试品灵活操作的耐环境机械臂，解决环境试验过程中不易对被试品进行操控使用的窘境，这对多种气候环境试验的充分验证有着至关重要的作用。本文从耐环境五自由度机械臂的机械结构出发，构建D-H 运动学模型[2]，预测机械臂可运动空间，并合理规划各个关节姿态，避免角速度和角加速度运动曲线的波动导致运动轨迹的偏差和关节间的碰撞。根据仿真结果可知，末端速度平稳，轨迹光滑连续，该机械臂具有较好的运动性和稳定性，具有一定的应用价值。

1 机械臂总体架构

耐环境机械臂的应用场景为高温、低温试验箱和低气压试验箱内，所以设计时应考虑总体系统对环境的耐受度。机械结构的材料应选择耐高温、耐低温的材料，电子器件应满足小型化、抗干扰、高可靠性、宽温域的特点。保证元器件、机械结构、舵机的可靠性，最终能实现机械臂在高温50 ℃、低温40 ℃即低气压47 kPa 下正常工作，在复杂环境下稳定运行，耐环境机械臂实物如图1 所示。

图1 耐环境机械臂实物图

对于机械臂的驱动方式，齿轮式驱动在转动精度、体积、运行效率和稳定性方面相较于气动式具有显著的优势，本文采用齿轮式的运动方式，采取舵机作为机械臂连杆间的驱动器件[3]。

该机械臂的主控芯片为STM32 控制器，控制板正常工作电压为（5～7.2）V。STM32 控制器具备对机械臂舵机进行高效操作的能力，其通过发出PWM 波的方式来驱动舵机的运行[4]。

2 机械臂运动学模型建立

通常正运动学和逆运动学构成机械臂运动学的两个方面，前者通过设定机械臂各关节参数来确定末端执行部件的位姿和状态，而后者相反，从预设好的的末端位姿反推每个关节对应变量。本文主要研究五自由度开链结构机械臂，使用标准型D-H 法（Standard D-H method）进行建模。

为得到机械臂相邻关节之间的必然联系，进而构建一个适当的机械臂运动学模型，需要对所有关节确定参考系，各种长度的连杆和可旋转的关节组成完整的机械臂。如图2 所示为标准型D-H 参数模型。

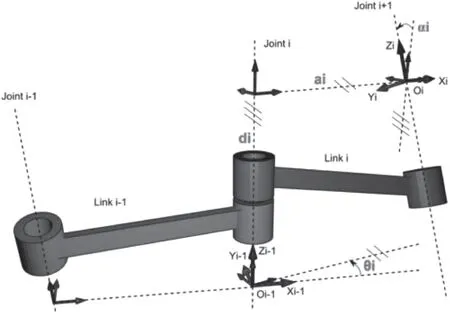
图2 标准型D-H 参数模型

D-H 法是对机械臂连杆和关节建模的方法，标准型D-H 参数模型建立的坐标系在连杆的后端，图2 中坐标系建立在Link i 的后端，本文设计的耐环境机械臂共五个连接杆，建模顺序为θ、d、a、α，即绕z 轴旋转角度、沿z 轴移动位移、沿x 轴移动位移、绕x 轴旋转角度四个参数，旋转关节在z 轴的旋转角度由关节偏执来定义。从机械臂的基座开始，依次分析相邻连杆间的几何关系，推出耐环境机械臂D-H 参数表，如表1 所示。

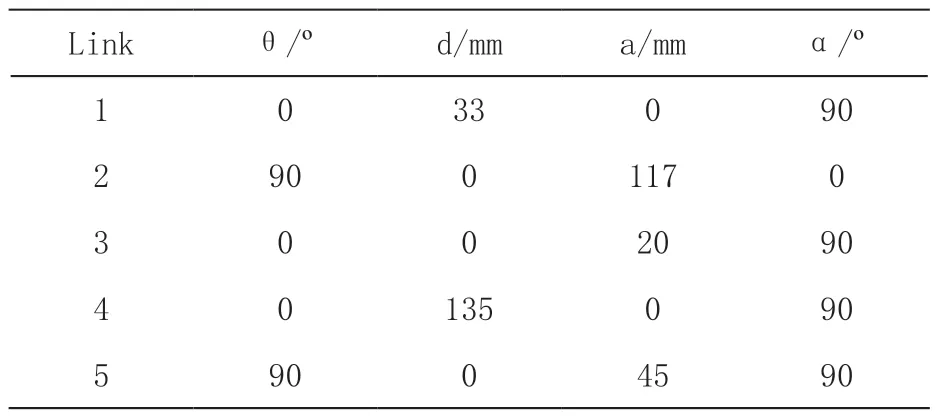
表1 耐环境机械臂D-H 参数表

3 机械臂的工作空间范围分析

机械臂的运动学模型的搭建可使用MATLAB 编程，并调用Robotics 工具箱中的相应函数，正向运动学仿真如图3 所示。

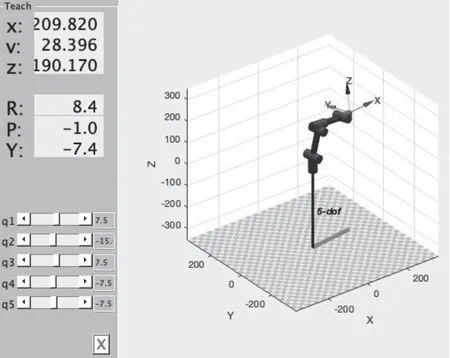
图3 五自由度的运动学仿真

通过 teach 函数显示建模图像界面并可实现对每一个关节的自由调节。qi 代表各个关节参数，其初始值默认为0。x、y、z 则表示末端坐标，由R、P、Y 三个参数来描述末端在空间中的姿态。

工作空间可视化是根据机器臂的长度、关节约束及末端活动范围对工作空间进行预先评估，对轨迹规划中末端坐标的确定有着重要的参考作用。本文采用了蒙特卡罗算法[5]来计算机械臂的操作域，求解流程图如图4 所示。此算法需分别为五个关节在限定范围内分配随机数值以生成随机角度值，然后依据这些角度值完成运动学模型上的正运动学解析，从而描绘出机械臂末端可能到达的所有空间点位，并据此创建点云图。

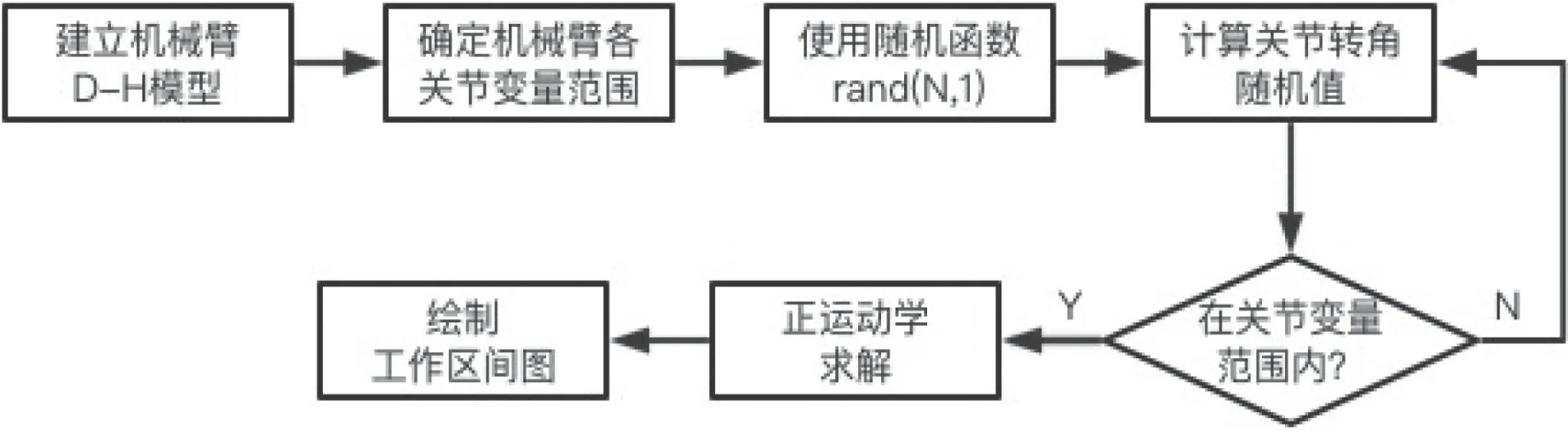
图4 蒙特卡罗法求解机械臂工作空间流程图

机械臂的工作空间主要受到其机械结构和舵机的转动范围的影响。当前已知机械臂各个关节的运动角度范围，在每个关节运动范围内，随机生成一个关节角度变量，通过正运动学fkine 函数得到相应的变换矩阵，再通过transl 函数得到三维空间下的坐标，并在空间内标记一个点。以此反复迭代，当标记点足够多时，可以近似描绘出机械臂的工作空间。机械臂的工作空间云图如图5 所示。

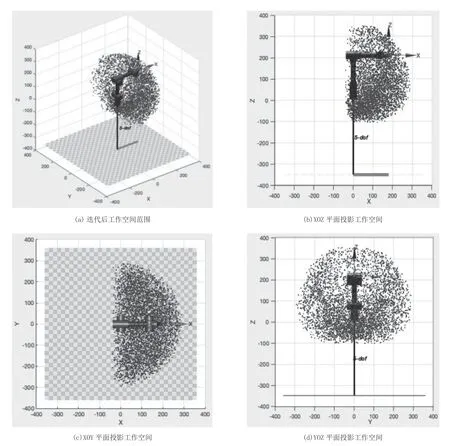
图5 机械臂的工作空间云图

经过5 000 次的选代，仿真模拟机械臂末端的工作空间范围云图呈球状，在图中可清晰的看到末端在X 轴、Y 轴、Z 轴的工作范围。机械臂的可运动范围与仿真结果一致，为机械臂末端轨迹规划范围提供了重要的参考依据。

4 轨迹规划

机械臂的轨迹规划是研究末端从初始位置到目标位置每个关节的运动过程[6]，过程中不得出现关节间相互碰撞，要求关节变化随时间的推进呈现连续光滑的曲线，不得有突变情况，曲线越平滑说明运动越稳定。对于机械臂末端的轨迹规划，常用多项式插值的方法，本文使用五次多项式插值算法，该算法根据速度和加速度约束，通过五次多项式对两点间路径进行约束和规划。在初末位置的变换矩阵再求逆解得到相应的关节变量，再对关节变量做轨迹规划。例如，当初始坐标和结束坐标分别设为[110，120，80]和[70，-150，100]，要求2 s 完成目标运动，使用jtraj 函数完成五次多项式轨迹规划仿真，得到机械臂末端的运动轨迹如图6 所示。

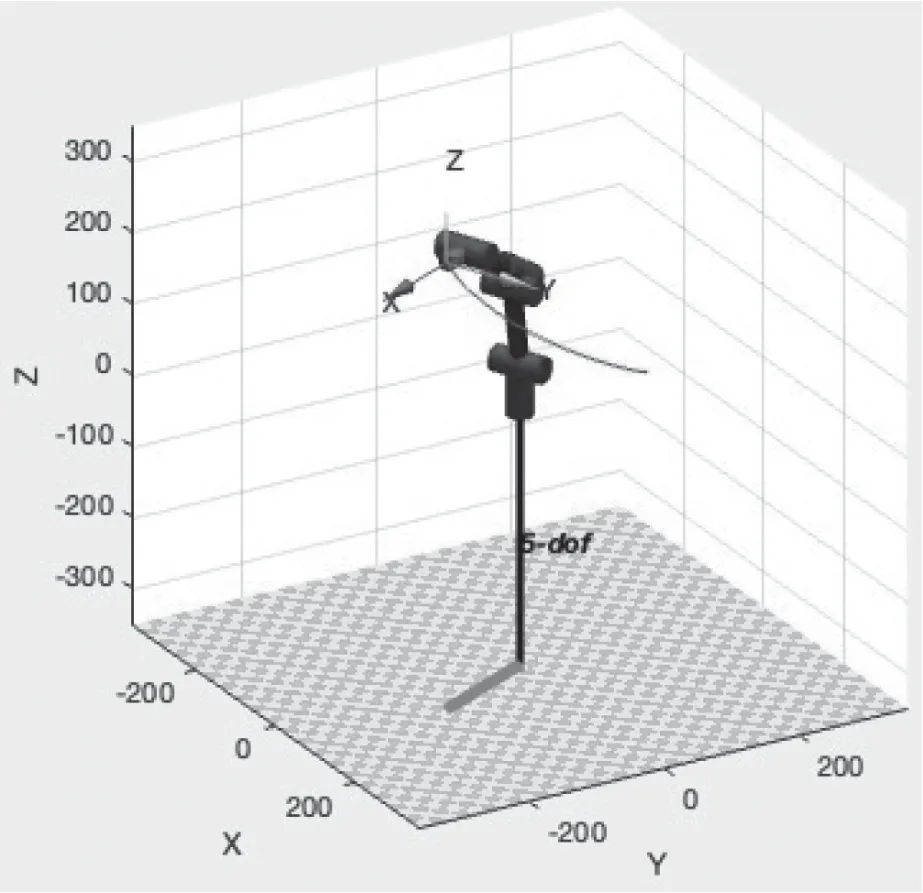
图6 机械臂末端的运动轨迹

通过计算多项式的插值，得到各个关节的关节变量q、关节速度dq、关节加速度ddq 的曲线，如图7 所示。

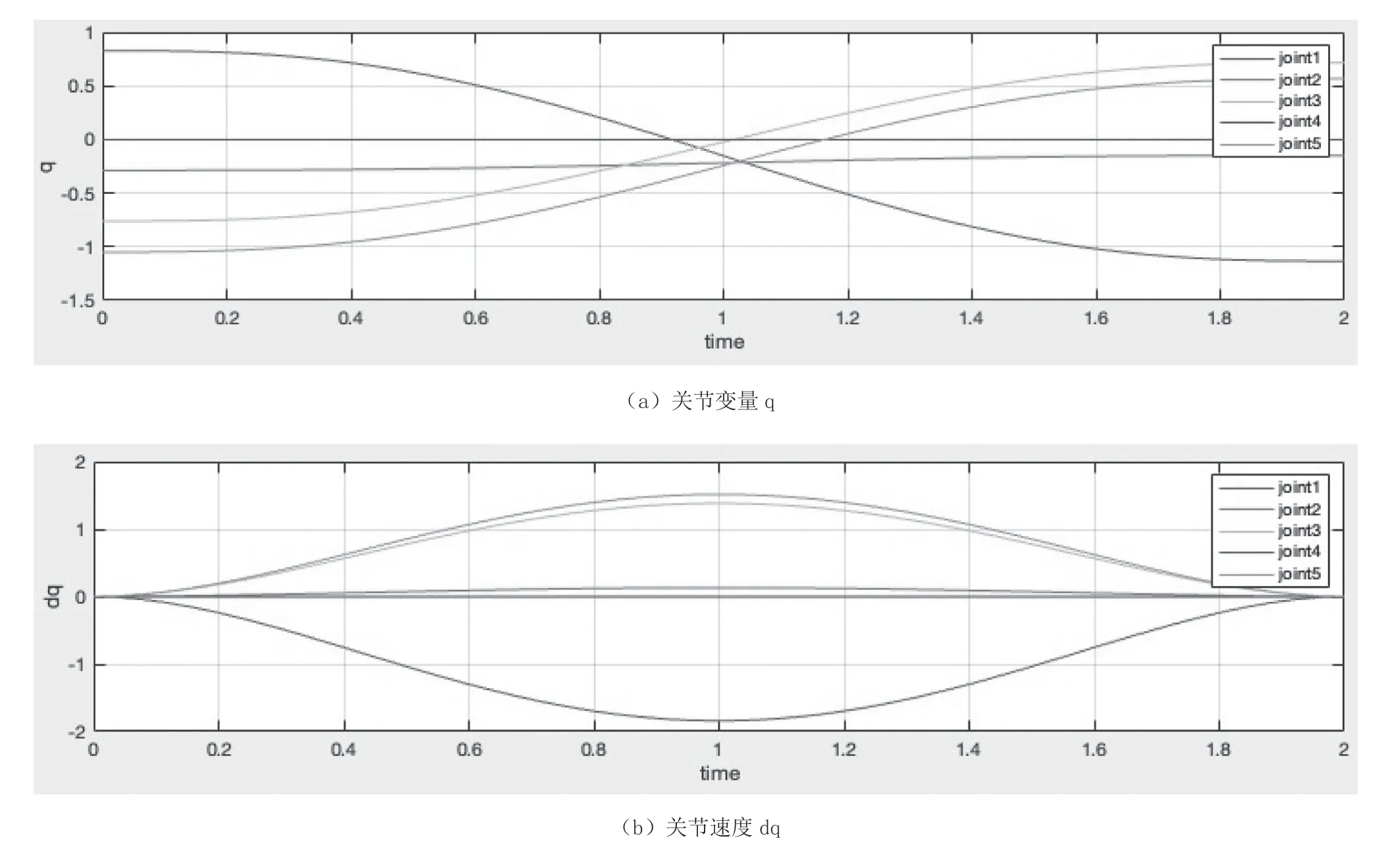
图7 关节动态参数

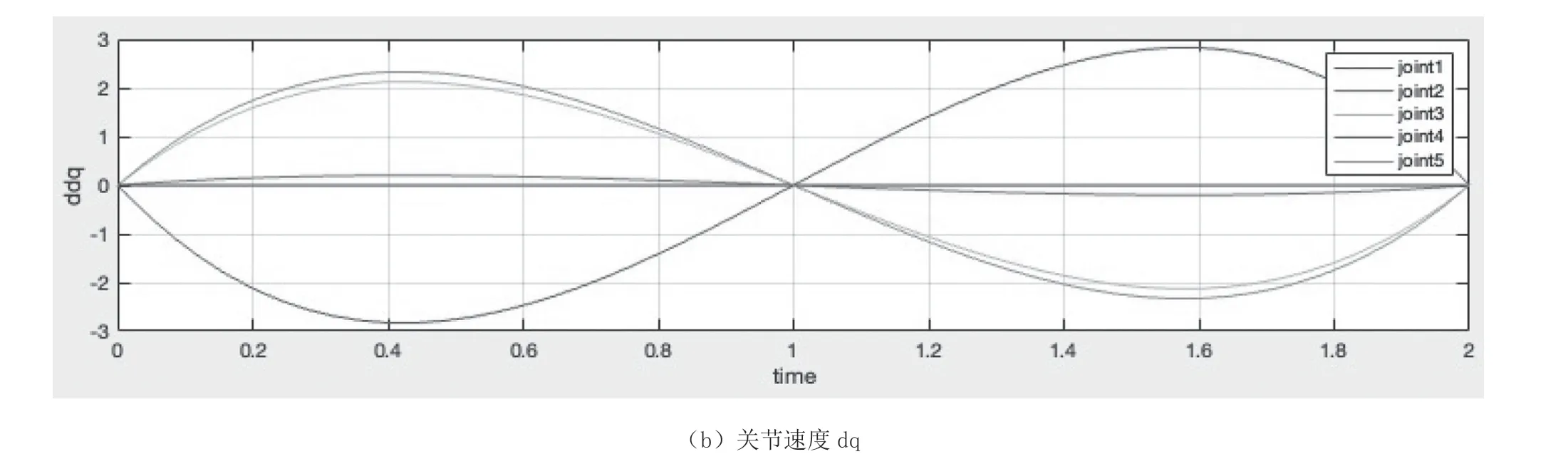
图7 关节动态参数（续）

由图7 可知，关节初末速度均为零，仿真动画较为顺滑，图像平滑工整。根据仿真结果分析可得，使用适当的路径规划策略能使关节变量、速度和加速度在整个运动过程中均处于连续平稳的状态，并且可以在短时间内维持机械臂的稳定操作。

5 结语

本文以耐环境机械臂为应用模型，进行总体架构分析，利用三维模型绘制出了连杆坐标系，进而确立D-H参数值，并构建其运动学模型。借助MATLAB 中提供的机器人工具箱，构建出五自由度的机械模型。采用蒙特卡罗法分析了耐环境机械臂的工作空间。根据机械臂的使用环境，研究耐环境机械臂的运动控制原理，并通过仿真试验验证了轨迹规划的可靠性，使用五次多项式插值算法显著降低机械振动的危害，保护设备免受过度磨损的影响，进一步增强了机械臂的工作效能，对被试品环境试验可靠性的提升有着重要作用。本文为今后对耐环境机械臂的深入开发提供了理论依据，后续可限制末端连接杆方位进行运动姿态的研究，实现机械臂对被试品按钮的点击操作。