一种提升变频压缩机转速波动抑制可靠性的方法

范凌云

（珠海格力电器股份有限公司，珠海 519000）

引言

永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）型变频压缩机，由于电机本体的齿槽效应、磁链谐波、定子电流分布不对称等因素以及压缩机负载力矩受各种外界不定因素影响导致其在低频工作过程中，转速波动尤为明显。当前余弦波转矩前馈补偿算法能有效地抑制变频压缩机在低频运转阶段的转速波动，但在压缩机不确定运行的状态下精确地补偿q 轴电流补偿量（iq_comp），还需确定负载变化形态。

本文提出一种带负载转矩观测器的转矩补偿方法，将有效地跟随工况变动而精确地调整低速波动抑制补偿电流值，则减小了余弦波转矩前馈补偿算法在负载发生变化时，未能以最佳补偿电流幅值提供q 轴电流补偿量（iq_comp）对压缩机转速波动抑制的影响，从而有效抑制变频压缩机在低频运转阶段的转速波动，提高空调的能效比与制冷/制热能力。

1 变频压缩机的转速波动

如图1 所示的压缩机工作过程和图2 所示的单转子型压缩机工作工程中的脉动情况：负载力矩、电电磁力矩和速度，由于控制系统的滞后性，压缩动作前，负载力矩越来越大，电磁力矩未能及时跟上负载力矩的变化，电机转速下降；反之，压缩动作之后，负载力矩瞬间减小，电磁力矩未能快速跟上，在电磁力矩的作用下，电机转速上升。由图1 可知由于电机在压缩机缸体内不均匀的圆周运动、冷媒吸排气压力等因素的影响，电机转速将产生周期性波动，其周期为压缩机的机械运动周期。产生这种周期脉动主要由于压缩机内部负载不平衡导致，这种不平衡状态在不同工况（压缩机吸气、排气压力不同）下，转速波动的初始角度会提前或者推后，波动大小会随负载大小波动，具有不确定性。

图1 压缩机工作过程

2 余弦波转矩前馈补偿方法

为了解决上述问题，家用变频空调常引进的解决方案是余弦波转矩前馈补偿iq_comp=iq_Ampcos（ωrt+θq_comp），其中iq_Amp为补偿幅值，θq_comp为补偿角度，ωr为机械角速度，能够有效解决转速脉动问题。补偿幅值与负载大小，即与q 轴电流iq*之间存在合理的比例关系，空间上和时间上的转速脉动可定量的计算加以解决，不同工况（压缩机吸气、排气压力不同）下，压缩机转速周期波动具有不确定性，通过加入转矩观测器，在负载突变的情况下，能及时观测到转矩的波动情况 ，通过Q 轴电流前馈补偿跟踪波动情况，提高电机转速稳定性。

3 基于Kalman 滤波器的负载转矩观测器

Kalman 滤波器是一种递推的计算方法，他是在线性最小方差估计基础上发展起来的,他对测量误差和干扰信号有较强抑制能力，被称为“最优控制”。从其被提出以来就广泛应用于信号检测和处理中，特别是在导航、定位等系统中[1-3]。电机的运动方程包含了负载转矩，一般情况下，负载转矩和转子位置会一起观测，称之为转子负载转矩观测器。Kalman 滤波器由于其固有的自抗干扰和迭代计算特性，转矩观测的精度和收敛速度点都具备优势。

3.1 波动角度与波动幅值计算

压缩机负载可以按照傅立叶级数展开，将其定义为：

式中：

TL0—负载基波分量；

TLn—负载n 次分量；

—压缩机当前转速下的平均速度；

周期性变化形成的基波负载的转速波动为：

式中：

—基波负载的转速；

—机械周期常数；

ar1—基波负载的加速度。

又有：

式中：

J—电机转动惯量；

Rs—定子线间电阻；

Pn—电机极对数；

ke—反电动势常数；

id—d 轴电流。

利用三角函数的正交特性,消去相关变量，式（4）可以变换为：

求解式（5）等号右边积分为：

联立方程式（3）、（4）和（6），最终可以得出负载转矩的相对偏移角度与基波的波动转速幅度：

根据基波的波动转速幅度Am1及不同频率和工况下按照实验效果确定补偿量的补偿系数kc，并计算补偿q轴电流幅值为：

式中：

3.2 负载转矩观测器

观测器的状态方程如下

式中：

Te—电磁转矩；

TL—负载转矩；

f—摩擦系数；

J—转动惯量；

ωr—转子机械角速度；

θr—转子位置。

写成矩阵方程的形式为：

式中：

在离散化过程中，将式（10）采用一阶欧拉法进行展开再计算，在此过程中对于误差的近似值需要进行补偿，此处采用Kalman 滤波器的反馈校正来完成。

记：

即离散方程可以写成：

在离散域中，系统状态方程如下，式子中w为输入噪声，称为系统噪声或系统误差，v为输出噪声，称为测量噪声或测量误差。

系统参数误差产生输入噪声，测量过程（尤其机械传感器的测量误差）产生输出噪声。输入和输出噪声其各自的平均值为零，属于高斯白噪声。

输入和输出噪声可以使用协方差矩阵来定义：

状态变量的估计误差也可以使用协方差矩阵来表示：

此处采用一种迭代的算法，其过程如下，也就是Kalman 滤波器：

1）分别进行状态变量的先验估计值的计算、协方差矩阵的先验估计值的计算：

2）Kalman 增益计算

3）状态估计使用测量量替代，再进行状态变量的最优估计值的计算

4）协方差矩阵计算

3.3 旋转坐标下q 轴电流的前馈补偿

如果使用前馈补偿，也就是将参考转矩通过观测到的负载转矩来进行修正，用转子位置和角度的观测值代替测量值，结合式（7）、（8）及Kalman 滤波器的迭代算法得q 轴电流补偿量为：

式中：

θc—为在不同频率和工况下按照实验效果确定的补偿角度。

为验证算法的可行性和优越性，选取1.5 P、电子膨胀阀、直流风机空调外机系统搭配海立GSX102SKQA6JL压缩机进行测试。

测试条件：

1）轻负荷—环温27 ℃；

2）重负荷—环温27 ℃+全堵冷凝器+风机转速调为450 rpm；

3）振动测试点为振动最明显的点——四通阀。

测试结果如表1 和图4 所示：

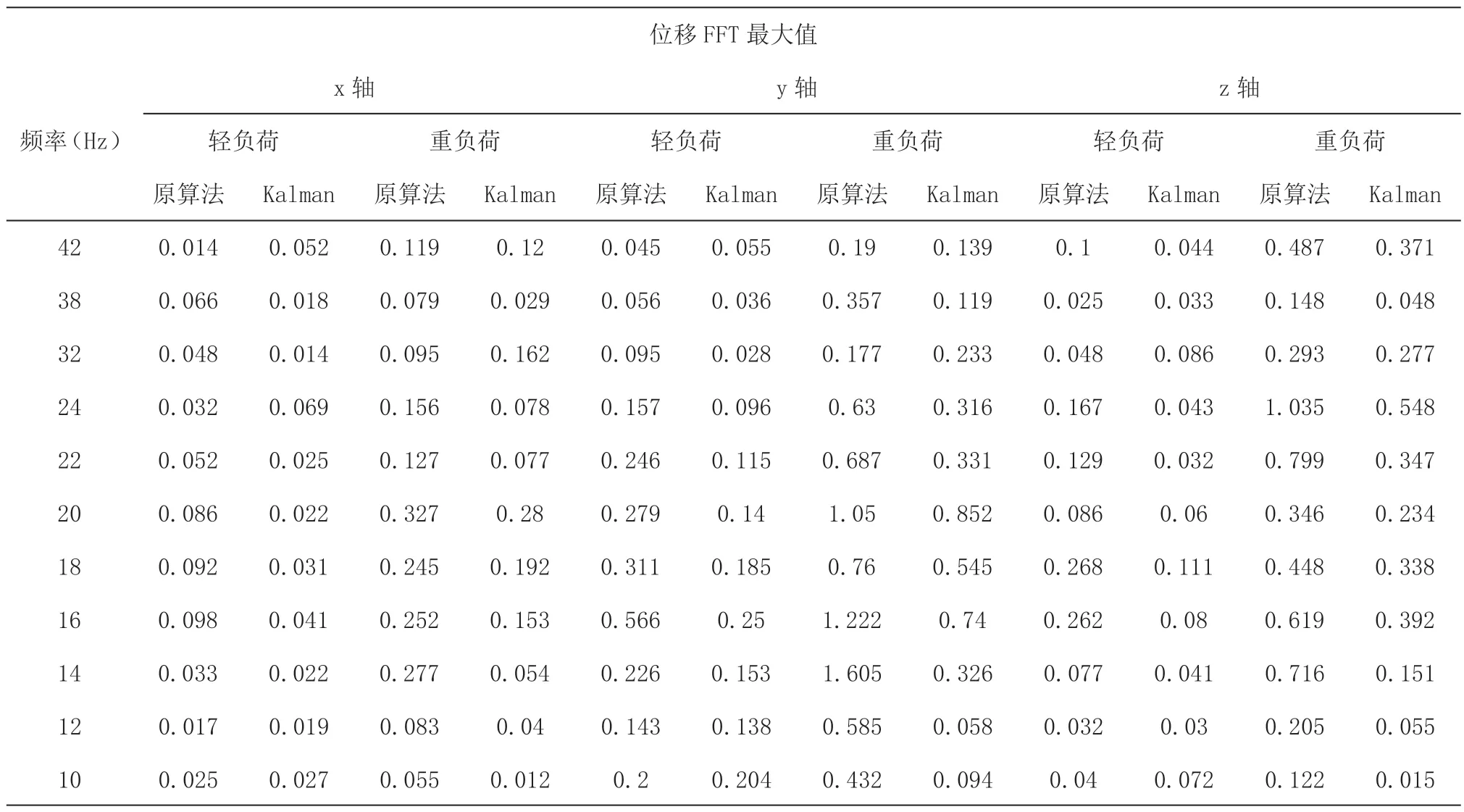
表1 两算法间转速波动抑制效果对比

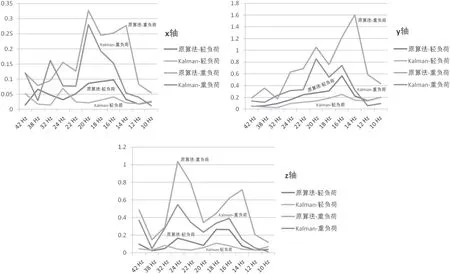
图4 位移FFT 最大值对比

1）负荷越重，频率越高（≥20 Hz），外机抖动越大。负荷越重，压缩机需求力矩越多，则补偿的电流越大，而原算法受可靠性的限制，补偿参数限制已调至保护前最大值，但Kalman 滤波器通过负载转矩的调整，相应的给予更多的电流补偿，使抖动得到进一步的抑制；

2）原算法轻负荷最优调试参数与重负荷最优调试参数略有差别，这是因为补偿幅值和补偿角度将随着负荷的变化而相应的变化，由于负载观测器最终补偿的电流仍然与幅值和角度相关，但其整体振动效果比原算法要较好一些，适应性更强；

3）原算法和Kalman 滤波器算法整体来看都在（16～22）Hz 振动较大，调整转补偿参数有一定效果，但效果不明显，则此段频率为该压缩机的震动点。

3.4 基于Kalman 滤波器的负载转矩观测器控制应用存在的技术难点

综上所述，基于Kalman 滤波器的负载转矩观测器控制与现方案的转矩补偿控制相比，在性能方面具有一定程度的提升，也具有进一步优化的潜力。

但在基于Kalman 滤波器的负载转矩观测器控制应用中还存在如下2 个技术难点：

1）Q 和R 值的设计。Q 和R 值的合理设计将直接影响到Kalman 滤波器的有效与否。需要说明的是，检测噪声v 协矩阵R 设计时需考虑低速大转矩永磁同步电机在低速运转时的特殊性。电机在低速运行时，转子位置的估算受位置估算算法的限制，将有较大的误差。若在某个控制周期内输出的位置信号偏差较大，则下一个迭代时刻，位置检测值仍然是过时的位置信息，和真实的位置信息之间可能存在较大的误差。这种情况下，就需要对位置检测值进行判断，选择适当的R 值。这一处理方法的物理意义在于，若当前周期的位置信息中存在较大的误差，由于v 较大，此时观测器反馈增益基本为零，不进行状态校正过程。

确定R 值之后，需要进一步分析系统噪声w 的统计特性，用以完成Q 矩阵设计。Q 设计的优劣将直接影响速度观测的动态性能及稳态精度。若Q 中元素选取过大，速度观测不能很好地发挥模型的预测作用，增加速度观测波动，降低观测精度；若Q 选取过小，速度观测过度依赖于模型，观测器动态性能下降，若模型中出现较大误差，观测算法还容易发散。考虑到 Q 矩阵关系到观测器的稳定性，为了防止算法发散，倾向于设计一个较大的Q 矩阵，从而将电机和编码器的模型误差都涵盖进去，但这样设计会导致速度观测精度降低。在实际的测速场合，一方面很难获取位置、速度和负载转矩这三个状态变量噪声之间的协方差；另一方面即使将Q 设计成非对角矩阵，在经过若干次迭代之后，和对角线上的元素相比，非对角元素也会下降至一个非常低水平。因此基于以上考虑，本文将Q 设计成正定对角阵，位置噪声、负载转矩噪声和系统速度噪声的方差分别是正定对角阵的对角元素。

2）受应用环境影响大。尤其对于运行状态与周围环境强相关的应用设备而言，无法实现完美契合。例如变频压缩机，其运行受周围环境影响大，因而对负载转矩观测器的要求更高，尤其在实时性、准确性和跟踪性方面，以便于适应压缩机周期快速变化的负载特性。此外，由于位置估算系统无传感器使得其本身存在滞后性，因此造成负载转矩的观测值总是滞后于实际值，如图5 所示。这是系统无传感器导致的固有滞后，使得转矩波动抑制效果受限，无法突破。因此对于变频压缩机而言，使用负载转矩观测器解决速度波动问题，关键在于提高应对负载突变的适应性和减少速度反馈的滞后，这样才能实现变频压缩机转速波动的有效抑制。

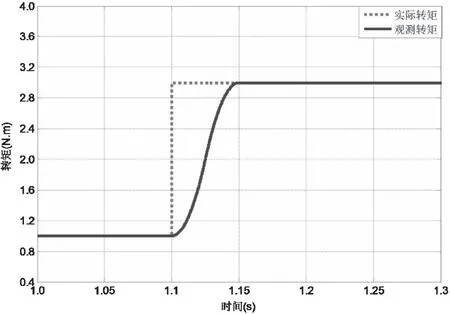
图5 实际负载转矩与观测负载转矩比较

4 结语

针对变频压缩机普遍存在的低频转速波动问题，本文提出一种带负载转矩观测器的转矩补偿方法，将有效地跟随工况变动而精确地调整低速波动抑制补偿电流值，有效抑制变频压缩机在低频运转阶段的转速波动，提高空调的能效比与制冷/制热能力。该控制策略具有效性和优越性，提高压缩机转速波动抑制的精确性和可靠性。