电动汽车动力电池安全风险评估研究

张晨佳，庞松岭，张璐璐

（1.海南电网有限责任公司电力科学研究院，海口 570100； 2.热带海岛智能电网实验室，海口 570100；3.海南电网有限责任公司，海口 572000）

引言

对动力汽车动力电池的健康状态进行安全风险评估，可以有效保障电动汽车安全。在对动力电池的安全风险评估上，由于在评估精度不理想、评估效果不好等，导致汽车安全难以达到保障[1]。电动汽车的电池安全风险评估，与其他的评估对象不同，需要通过外部分析，并结合数学方法进行分析，目前主要的安全风险评估方法中，主要有电化学模型、等效电路模型、数据驱动方法等几种，但在实现电动汽车动力电池的实时评估上，依然存在一定的不足，并且容易有建模难度较大，鲁棒性较差，导致评估过程出现误判等。

在电动汽车动力电池寿命周期内安全风险评估方法的研究上，目前主要有以下几种，文献[2]在基于改进TCN 模型基础上，评估汽车的动力电池健康状态，达到在不用考虑电动汽车的电池内部化学反应情况下，对电动汽车动力电池进行评估。文献[3]提出基于数据仿真模型，分析电池内阻等健康参数，同时引入贝叶斯极限学习，对电池的荷电状态进行分析评估。文献[4]使用 GRURNN 模型结构，建立电池样本数据集，使用电池样本数据集，达到对电动汽车动力电池寿命周期内的安全风险评估。本文在这些研究之上，将电池电压偏差纳入考虑，分段计算电池电压均方差，更准确地评估动力电池的状态和安全风险。通过一致性辨识模型确定安全风险因素权重，避免主观判断和不确定性带来的评估误差，提高评估结果的可靠性和准确性。借助TCN 结构作为评估的基础框架，将电池电压均方差代入目标层，综合考虑各项安全风险因素，实现电动汽车动力电池的梯次综合安全风险评估。

1 电动汽车动力电池寿命周期内安全风险评估方法

1.1 基于电压偏差计算动力电池电压均方差

为了达到对动力电池的安全风险有效评估，在基于电压偏差下，计算动力电池电压均方差。利用电压偏差特性，将动力电池电压曲线分为低荷电状态、中荷电状态、高荷电状态，在分段情况下，计算动力电池平均电压v，公式表示为：

式中：

n—动力电池电芯数量；

i—动力电池数量；

vi,t—i个动力电池在t时刻的电压参数。

根据动力电池电压协方差，计算电压均方差σ，得到的公式为：

式中：

k—时间段的数量；

c—分段的动力电池电压协方差。

对低荷电状态、中荷电状态、高荷电状态三个电荷状态，分别进行计算，得到三个电荷状态下的电压均方差。

通过测量电动汽车动力电池的电压偏差，计算得出电压的均方差。这个指标可以量化电池电压的离散程度和变异性，电压均方差越大，表示电池的电压不稳定性越高，存在安全风险概率越大。

1.2 基于一致性辨识模型确定安全风险因素权重

基于一致性辨识模型，确定其安全风险模糊权重。建立电动汽车的安全风险评估结构，目标层为动力电池电压风险分析，动力电池充放电风险分析为准则层，指标层为风险程度[5-6]。提取动力电池电压均方差σ，并代入安全评估矩阵的目标层，以此建立一致性辨识矩阵，计算单层次的权重，公式为：

式中：

—风险矩阵i 行j 列元素；

—风险矩阵i 行j 列元素隶属度；

—风险矩阵中各元素对于风险评估的贡献程度。

以此建立可能度p，公式为：

式中：

o—因素模糊数；

t—风险评分可能性；

g—评分参数。

从而得到一致性辨识模型，电动汽车电压风险可能度为：

式中：

δ—电压分配参数。

从而得到一致性辨识判断矩阵，并以此得到安全风险因素权重为：

式中：

β—风险排序向量，得到ς为最终安全风险因素权重，用于计算安全风险模糊权重和综合偏离度，以实现对电动汽车动力电池的梯次综合安全评估。

1.3 电动汽车动力电池梯次综合安全风险评估

使用安全风险模糊权重，通过安全风险因素权重ς计算各个指标或评估维度的风险程度,对电动汽车动力电池进行综合性评估。使用AHP 层次分析法，对电动汽车的动力电池一致性方面进行综合性评估[7]，评估流程如图1 所示。

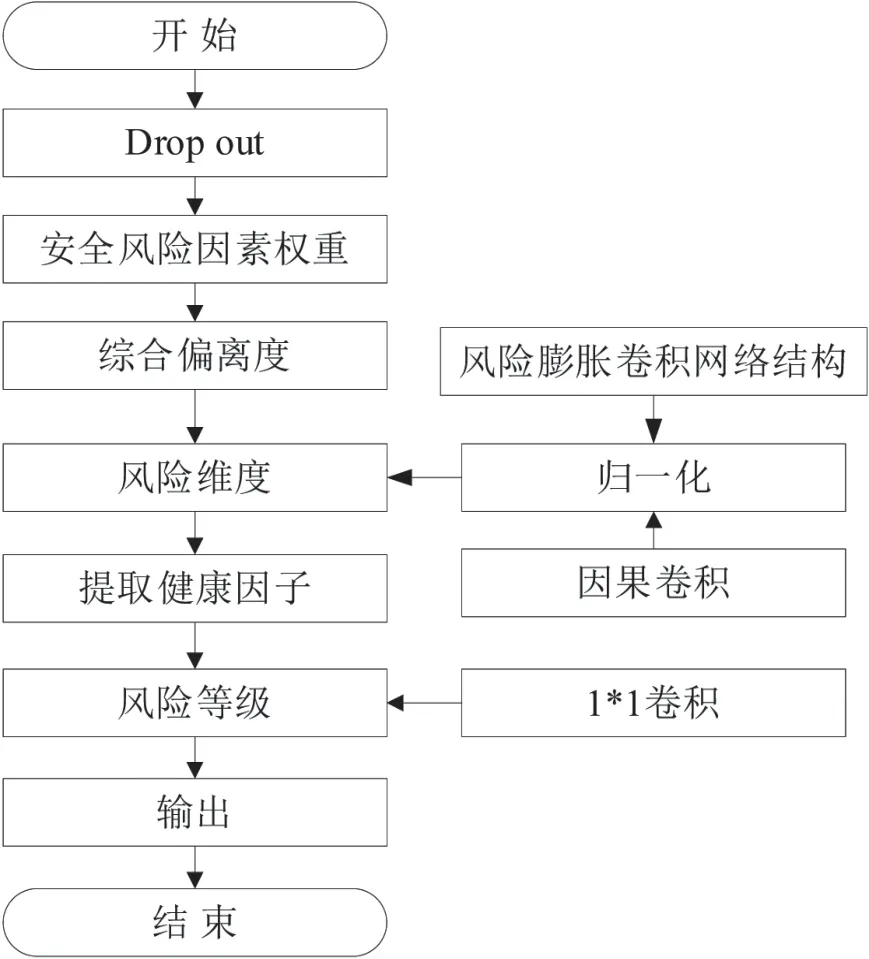
图1 综合安全评估流程

通过挖掘数据特征与风险之间的关系，形成膨胀卷积网络结构，其结构示意图如图2 所示[8,9]。

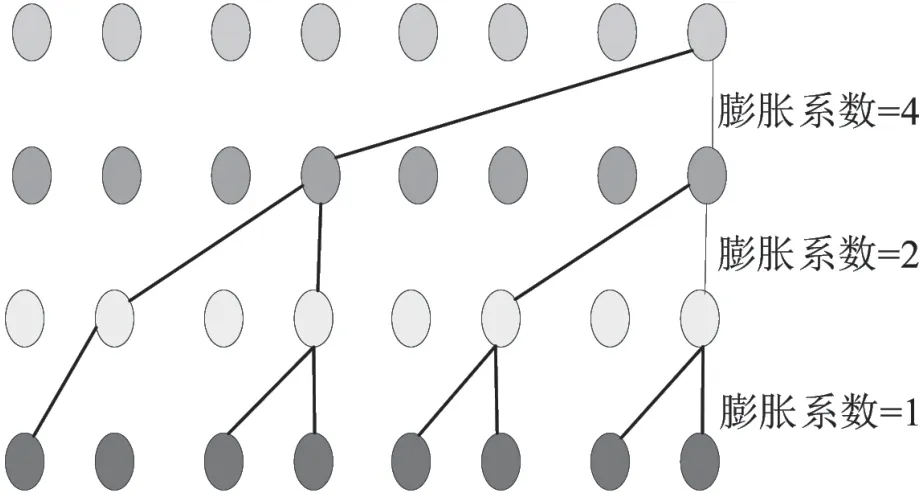
图2 膨胀因果卷积网络

对风险维度进行调整，以TCN 结构作为评估的基础框架，对健康因子进行提取，TCN 结构如图3 所示。

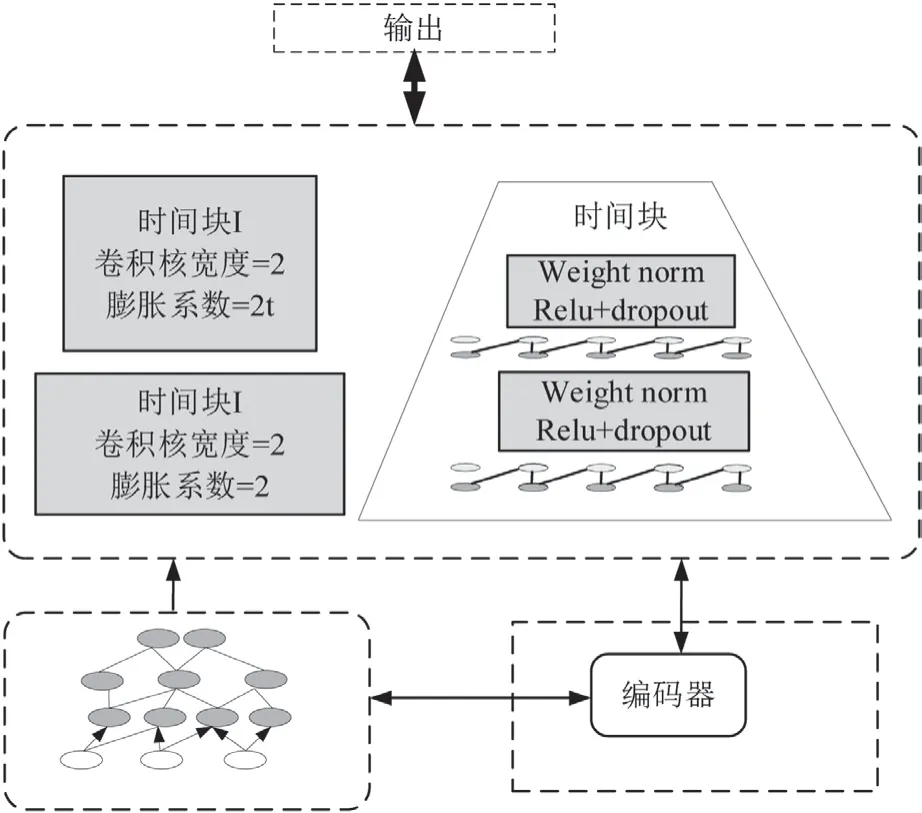
图3 TCN 结构

根据结构计算安全风险模糊权重，将安全风险评估指标进行对比，得到综合偏离度，公式为：

式中：

e—安全风险的负荷参数值；

y—安全风险的电压参数值。

根据提取的健康因子，设置安全风险等级以及对应的状态，如表1 所示。

表1 风险等级划分

根据划分的风险等级，在TCN 模型的因果关系下抓取[10]，对电池状态进行计算与匹配，得到电动汽车动力电池的梯次综合安全评估结果。

2 实验与分析

为了验证所设计方法对于电动汽车动力电池的安全风险评估效果，进行实验。

2.1 实验装置

使用最大压力为2 000 N 的XYY-QD500 型电子万能试验机进行静态压痕实验，压头类型为半球头，通过Opus BT-C3100 V2.2 数字电池容量测试仪对电池的电压进行监控。同时，使用320×240 像素的FLIR E75 型红外热像仪来监控电池的温度变化，以达到对动力电池安全风险状态的实时监控。

电压监控参数：采样频率为每秒钟采集一次；最大电压设置为5 V。

红外热像仪参数：像素分辨率为320×240 像素；测量范围为（-20 ～150）℃；每30 s 拍摄一次热像图像。

2.2 实验数据

使用Arbin 电池测试仪，对动力电池数据进行测量，进行记录，电池尺寸为65 mm*28 mm、电池阴极为LiCoO2、标称容量为1 100 mAh、放电温度为（-20 ～50）℃、充电温度为（0 ～50）℃，充电电压为4.2 V。选择30 个电动汽车的动力电池进行实验，进行编号，依次为Dc10- Dc40。

在0.75 A 的恒流模式下进行充电，当电压为4.2 V 时，选择40 个电动汽车的动力电池进行实验，电池的实验信息如表2 所示。

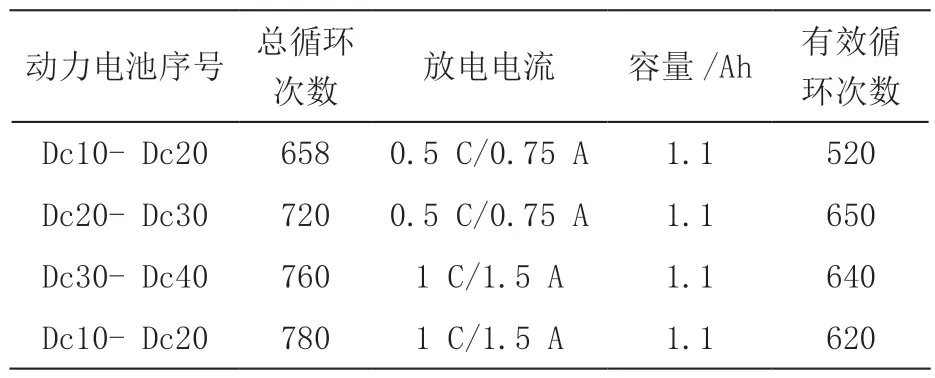
表2 实验动力电池信息

电动汽车的动力电池，在0.75 A 的恒流模式下进行充电，当电压为4.2 V 时，进行第二阶段的充电模拟。

2.3 动力电池健康因子的选取

选择恒压充电过程中，动力电池电压从2.5 V 上升至3.7 V 时间作为第一阶段，记为A1；动力电池电压从3.7 V 下降至2.5 V 时间作为第二阶段，记为A2；动力电池电压从2.5 V 回升后阶段作为第三阶段，记为A3，以此选择动力电池健康因子参数，对动力电池风险程度加以评估。

动力电池健康因子的选取过程如图4 所示。

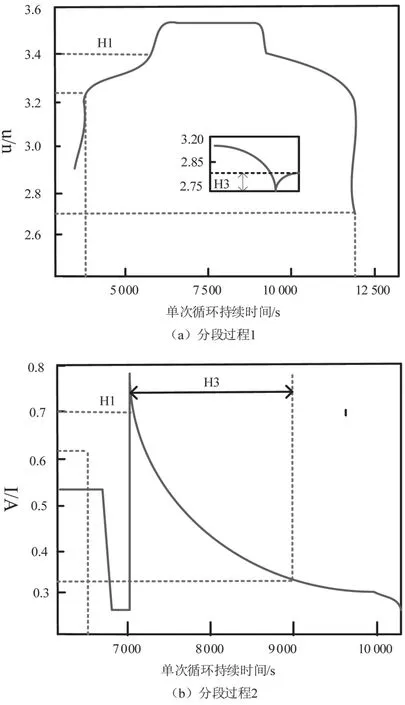
图4 动力电池健康因子选取过程

根据图4 结果，使用皮尔森相关系数，对评估因子进行验证，验证公式如下所示：

式中：

—第i 次循环的电池风险；

—第i 次循环的动力电池健康因子。

将选择的动力电池健康因子进行代入，得到系数，如表3 所示。

表3 动力电池健康因子相关系数

从表3 中可以看出，选取的动力电池健康因子，其皮尔森相关系数均在[-1，1]之间，并且绝对值均在0.8以上，说明选择的动力电池健康因子具有可行性，可用作此实验的评估。

选取的动力电池健康因子，其皮尔森相关系数均在[-1，1]之间，说明选择的动力电池健康因子具有可行性，可用作此实验的评估。

2.4 实验指标

实验选择绝对误差、评估均方根误差、评估平均误差对评估的精度进行评价，其公式如下：

评估绝对误差；

评估均方根误差：

评估平均误差：

式中：

a—评估次数；

—评估值。

2.5 评估结果分析

使用本文设计方法，以及其他两种方法进行实验，可以对于四组电动汽车的动力电池进行安全分析评估后，得到评估结果的绝对误差图像，如图5 所示。

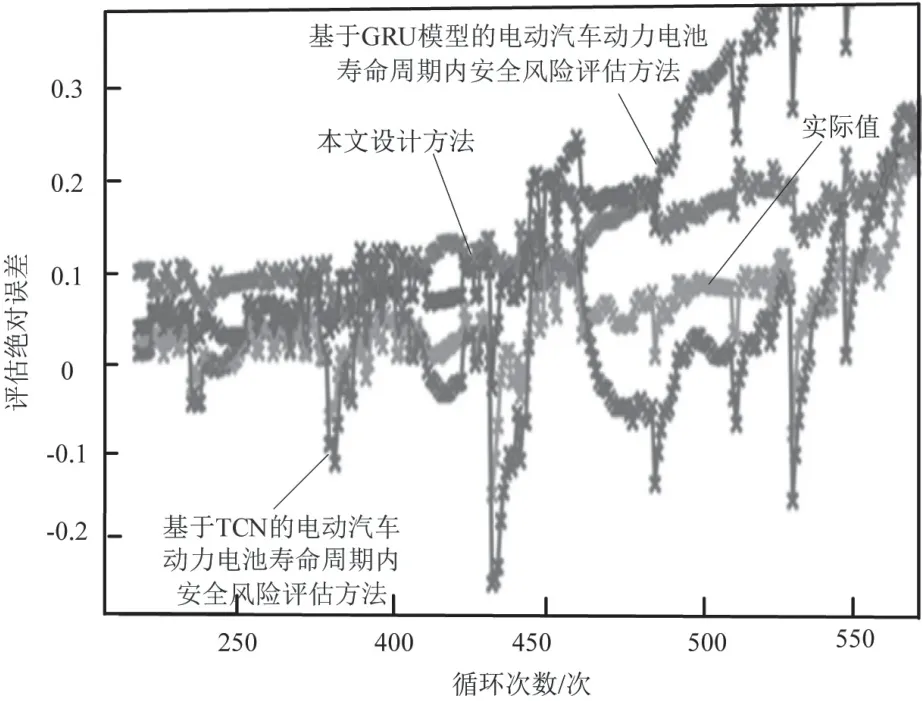
图5 评估结果绝对误差

图5 中可以看出，使用本文设计方法，在进行安全分析评估后，得到的绝对误差几乎趋近与0，说明其评估的绝对误差相对较小。

三种方法下，对四组电动汽车的动力电池评估的评估均方根误差与评估平均误差对评估进行统计，情况如表4 所示。

表4 不同方法下的均方根误差与平均误差统计

从表4 中可以看出，相对比其他两种方法，本文设计的方法，安全风险评估的均方根误差相对较小，平均达到了0.012，安全风险评估的绝对平均误差相对也较小，平均达到了0.007。综合三类评估误差指标，可以看出，本文设计的方法，在安全风险评估上，其精度较高。其主要原因在于，在基于电压偏差下，将动力电池负荷分为低荷电状态、中荷电状态、高荷电状态，分段计算其电池电压均方差，减少了其他因素对评估的影响。该方法可适用于电动汽车动力电池寿命周期内安全风险评估。

3 结束语

本文对电动汽车动力电池寿命周期内安全风险评估进行研究，经实验得出以下结论：

1）通过使用本文设计的方法进行动力电池安全分析评估，评估结果的绝对误差相对较小，说明评估准确性较高。

2）本文设计方法在均方根误差和平均误差相对较小，说明评估精度较高。

3）本文设计的方法利用了动力电池在不同荷电状态下的电压偏差分析，减少了其他因素对评估结果的影响。

在未来的研究中，可以引入更多的指标或因素，探索不同的评估模型或算法，进一步改进动力电池综合安全评估方法，以提高评估的准确性和全面性，适应不同类型的动力电池系统和实际应用场景。