厘清运算对象与法则,探究运算思路和方法——以高考中的“函数”问题为例谈数学运算素养的培养

车 慧

江苏省无锡市辅仁高级中学

数学运算是“新课标”中提出的数学六大核心素养之一.因此,数学运算在高考中受到了高度关注,“成也运算,败也运算”,几乎成为一种共识.从当下高中数学教学的现状来看,学生的数学运算能力在整体表现上依然比较“孱弱”,“一听就懂,一做就错”的现象普遍存在.采取切实有效的措施,使数学运算素养在课堂教学中落地生根,是一个值得我们高度重视的课题.下面以高考及其模拟试题中的“函数”问题为例,谈谈笔者的一些认识和体会,供大家参考.

1 弄清运算对象,找准运算方向

数学运算素养是在明晰运算对象的基础上,依据运算法则解决数学问题的一种素养.对于具体的数学运算,我们要结合运算情境,正确地分析并弄清数学运算对象,深刻认识运算对象的特征,挖掘其内涵,明确运算的方向,以理性思维为基础,合理地将问题加以变形与转化,进而通过正确的运算使问题获得解决.

分析：根据题设条件,结合所求结果中代数式的结构特征,对比最值或取值范围求解的一般形式,确定运算对象,合理联系对应的基本不等式的有关知识,通过基本不等式的变形公式的应用来分析与求解,简捷有效.而涉及分式函数的最值求解问题,则可结合运算对象的确定,直接利用对勾函数的图象与性质,或借助函数与导数的有关知识,通过合理的运算使问题获得解决.

点评：弄清相应的运算对象是解决数学问题的一种最基本的思维方式,只有弄清了运算对象,才能知道怎么处理运算对象,运算才有方向感.在本例的求解过程中,根据问题的条件和目标,分析它们之间的联系,根据运算对象的结构特征,合理地联想由基本不等式引申变形而得到的公式(柯西不等式)及其成立的条件,通过运算实现问题的转化,找准运算的方向,再通过相应的数学运算获得了结果,问题迎刃而解.

2 理解运算法则,明晰运算依据

数学运算是在一定的法则下进行的,理解数学运算的法则,明晰数学运算的理论依据,是数学运算得以顺利实施、取得正确结果的基本保证.解决数学问题,在弄清了运算对象以后,紧接着就要思考“需要进行哪种数学运算?相应的运算法则是什么?”在正确认识和理解相应的运算法则的基础上,确定运算思路和途径,进行科学合理的数学运算,为问题的解决开拓出一个全新的局面.

例2(2023年全国乙卷·16)设a∈(0,1),若函数f(x)=ax+(1+a)x在(0,+∞)上单调递增,则a的取值范围是______.

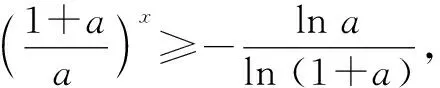
点评：理解数学运算的法则,明晰数学运算的依据,是让运算能够沿着既定的方向顺利进行的有力保证,对于解决一些与函数、方程和不等式有关的问题有着独特的功效.这里借助导数将函数的单调性问题转化为不等式恒成立,再借助参变分离的方法,利用指数和对数的运算法则巧妙地求出a的范围,使问题获解.

3 选择运算思路,设计运算程序

解决数学问题,一项十分重要的工作就是结合题目中的条件与结论的分析,通过理性思维打通条件向结论转化的途径,找到解题的思路,在明晰算理的基础上设计出运算的程序.结合问题的具体情境和基本特征,选择恰当的运算思路,设计合理的运算程序,算思结合,以思助算,无疑会对提高运算的效率、提升学生的思维品质起到很好的促进作用.

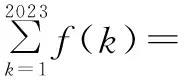
分析：根据题设条件,将抽象函数的奇偶性进行等价转化,通过函数基本性质的确定,探究运算思路,为问题的求解打开局面.

解析：因为函数y=f(x)的定义域为R,且f(x+1)为偶函数,f(x-1)为奇函数,则f(1-x)=f(1+x),f(-x-1)=-f(x-1),所以,函数f(x)的图象关于直线x=1对称,也关于点(-1,0)对称.所以,f(-x)=f(x+2),f(-x)=-f(x-2).所以f(x+2)=-f(x-2),则f(x+8)=-f(x+4)=f(x).由此可知,函数y=f(x)是以8为周期的周期函数.

由题意,当x∈[-1,1]时,f(x)=1-x2,则f(1)=0,f(7)=f(-1)=0,f(8)=f(0)=1.

所以f(2)=f(0)=1,f(3)=f(-1)=0,f(4)=-f(-6)=-f(2)=-1,f(5)=f(-3)=-f(1)=0,f(6)=-f(-8)=-f(0)=-1.

点评：这里,基于函数的奇偶性、对称性、周期性之间关系的视角去分析函数的求值问题,将函数的奇偶性等价转换为函数的周期性,运算思路的选择和运算程序的设计,沟通了题目的条件和结论之间的联系,实现了问题的转化,使问题获得简捷巧妙的解决.

4 感悟运算方法,提升运算技能

培养学生的数学运算素养,不仅要让学生弄清运算对象、理解运算法则,使学生学会选择运算思路、设计运算程序,更要让学生掌握运算方法,提升运算技能.一个数学问题的解决,往往有多种方法,教学中,要注意指导学生通过观察、分析和比较,从这些方法中选取运算步骤少、变形简便、运算量小的最佳方法,使得解题运算科学合理、省时省力.

例题略.

“数学运算”并不是简单的数学计算,“数学运算”主要是对运算对象、运算法则、运算思路、运算方法等方面的理解、掌握、探究和选择,因此,提升学生的“数学运算”核心素养显得尤为重要.为促进学生“数学运算”核心素养的提高,倡导教师:(1)讲授新课时,应该将概念讲清楚,讲透彻,加强概念教学,注重概念的引入,分析概念的含义,了解概念的本质,掌握概念的内涵与外延,从多角度入手,加深学生对概念的理解.让学生能在概念与概念间建立联系.(2)讲授习题课时,将习题所涉及到的知识点,思想方法讲清楚,讲明白,帮助学生对相关知识制作思维导图,使零散的知识点建立起直观的联系.(3)复习课不要盲目刷题,多变式教学,一题多解.打破机械、套路、思维定式的答题思路,提升“数学运算”核心素养,维持关联结构水平并向拓展结构水平迈进.