新型变极化角反射器设计及散射特性分析
陈焱 王占领* 肖科 庞晨 计一飞 李永祯 王雪松
(1.国防科技大学电子科学学院 电子信息系统复杂电磁环境效应国家重点实验室, 长沙 410073;2.国防科技大学电子科学学院电子科学系, 长沙 410073;3.国防科技大学电子科学学院智能感知系, 长沙 410073)
0 引 言
角反射器是一种高效的对抗雷达探测的无源干扰装置,具有作用频带宽、干扰效果明显、作战效费比高等优势,被广泛用于关键军事要地和军事目标的防护[1].角反射器一般由互相垂直的两块或三块金属面板构成,入射电磁波在其内部产生多次反射,使雷达来波沿入射方向反射回去,因此具有很强的雷达散射截面(radar cross section, RCS)[2].按照反射面数量的不同,常见的角反射器可分为两面角、三面角、八面角、十二面角等.在实际作战中,角反射器既可以用来模拟包括坦克、舰船、飞机等地/海/空中目标,又可以利用其强散射特性扰乱目标的雷达特征[1],起到保护我方重要目标的目的.
常规的角反射器并不具备自适应能力,一旦加工完成,构型相对固定,因此散射特性固化,无法对回波进行灵活调控,容易被抗干扰算法鉴别,干扰效果受到限制.近年来,研制电磁特征灵活可控的新型角反射器是无源干扰装置的一个重要发展趋势[2-5],这对于弥补传统自卫式无源干扰技术的不足,降低高价值目标的发现概率,具有重要的理论研究价值与军事应用意义.
极化作为电磁波的本质属性,是幅度、频率、相位之外的重要基本参量,能够反映目标的姿态、结构、尺寸等物理特征[6].随着极化雷达的发展,极化信息获取和利用已成为目标探测识别的有效手段之一.在目标识别领域,已有针对角反射器极化特性开展的一系列研究工作[7-10],为角反射器类虚假目标的鉴别提供了理论支撑.在具备极化调控能力的干扰器件研究方面,受二维超表面技术发展的推动,近年来出现了极化可调超表面相关研究,文献[11]中理论和实验表明基于超材料的极化转换器的转换效率高达90%.在极化调控超材料设计方面,比较有代表性的是编码型有源极化转换表面[12-14],这类极化调控超表面通过在单元上加载可变元器件,并通过外加激励来改变元器件的参数,从而改变单元结构的谐振状态,使其反射特性随之改变.通过加载有源器件的方式来实现极化调控,提高了电磁波调控的灵活性,但需要精心设计控制电路.
本文借鉴超材料的思想,设计了一种无需额外加载有源器件的极化栅,将极化栅加载在常规雷达角反射器上,通过控制极化栅的旋转,实现角反射器散射场极化状态的实时变化、灵活调控,从而扰乱雷达回波,使对方雷达难以鉴别.将极化栅变极化技术应用于常规角反射器,既保留了角反射器的强散射性,又弥补了其灵活性差的缺陷,为新型电磁特征可调可控角反射器的研究提供了新思路、新方法.
1 变极化角反射器设计
1.1 传统角反射器散射理论
雷达角反射器的工作原理是利用偶镜原理,将三个互相垂直的镜面装在一起,三条公共棱边相当于三个偶镜,因此光线无论从什么角度照射到它上面,都会沿着原来的方向反射回去.当雷达波束遇到角反射器时,由于每个表面的镜面反射,会使波束最后以反转180°的方式反射回来波方向.因此,当三面角反射器各平板相互正交时,在一个很宽的观察角度范围内能够呈现出很大的RCS,从而可以有效干扰跟踪雷达、无线电信标等目标.可见,传统的金属无源角反射器具有结构简单、性能稳定、架设容易、成本低廉等优点.
角反射器根据几何结构的不同通常可分为:方形、三角形、圆形三种类型[15].构成角反射器的每个表面可认为是理想导体板(perfect electric conductor,PEC),以方形角反射器为例,假设其垂直边长为a,坐标原点与角反射器三条公共棱边的交汇点重合,x轴、y轴、z轴分别为三条公共棱边的延长线,其三维散射模型如下[15-16]:
式中:A=; θ为雷达视线方向与z轴夹角; ϕ为雷达视线方向在xOy平面上的投影与x轴的夹角.角反射器的最大反射方向为ϕ=45°,θ=54.735 6°,即为正入射方向,其RCS 值的解析表达式为
将角反射器的RCS 与1 m2PEC 的RCS 比较,得到归一化RCS:
以边长为0.1 m 的方形角反射器为例,当入射电磁波频率为10 GHz 时,根据式(2)、(3)计算得σmax=6.2 dBsm.当用垂直极化平面波照射时,经角反射器反射后回波的垂直极化分量和交叉极化分量的RCS 分布如图1 所示,最大值出现在ϕ=45°,θ=55°附近.对比图1(a)和图1(b)中各极化分量的RCS 可见,角反射器口径面内的散射回波以垂直线极化为主,与入射波极化状态一致.因此,常规角反射器对散射回波不具备极化调控能力.
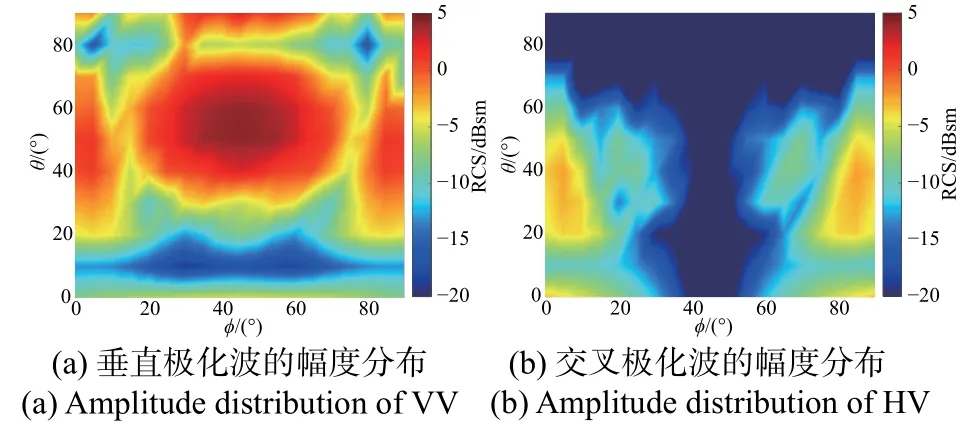
图1 方形三面角反射器口面内RCS 分布Fig.1 RCS distribution of the square trihedral corner reflector in the plane
1.2 极化栅极化调控原理
图2 给出了极化栅结构示意图.如图所示,该极化栅是在圆形PCB 板中均匀嵌入多个金属条,即栅条,圆形PCB 板用于固定栅条,以使变极化器在旋转过程中不发生形变,从而降低变极化器旋转对极化状态调制效果的影响.令相邻两个金属条的间距为d,栅条的厚度为t(栅条在垂直于栅板平面方向的宽度),栅条宽度为w,最优状态下,栅条之间相互平行,相邻栅条之间的间距相等.利用栅条产生结构色散效应,即电磁波在不同介质中存在不同的传播波长,从而产生相位差.

图2 极化栅结构示意图Fig.2 Geometrical sketch of the polarization gate
在极化栅工作时,栅板绕其几何中心O,在其所在平面内以角速度 ω转动,栅条的方向不断变化.根据栅条倾斜角度,定义与栅条平行的极化分量为EHi,与栅条垂直的极化分量为EVi.对于EVi,传播波长为λ0;对于EHi,由于存在截止波长,所以传播波长为 λg,且
式中: λg为波导波长; λ0为工作波长; λc为TE10模截止波长.
因此,电磁波经栅条反射后,EVi与EHi分量之间相位差 Δφ为
这是由于当入射波经过极化栅时,电磁波在栅条中的极化分量EHi波长被拉长,极化分量EVi波长保持不变,则极化分量EHi的相位产生滞后,从而与极化分量EVi间存在相位差.此外,由于极化栅为非理想金属,入射波经过极化栅后各极化分量有不同程度的衰减.综上所述,极化栅通过调制入射波各极化分量的幅度和相位,实现对电磁波极化状态的调控.
1.3 变极化角反射器设计理论
图3 为所提出的新型变极化角反射器的结构示意图,该角反射器由传统的方形三面角角反射器和圆形极化栅两部分组成,通过机械控制极化栅绕自身几何中心旋转,入射到极化栅上的电磁波经过极化栅的两次调制,反射波的极化状态发生改变.以入射波为垂直线极化波为例,栅板按一定的角速度绕中心点转动,经角反射器反射后的电磁波可经历垂直线极化、水平线极化、左旋圆极化、右旋圆极化等极化状态.作为干扰源使用时,极化状态的改变导致极化方式固定的雷达天线无法有效接收雷达回波,同时,随着极化栅旋转角度的变化,雷达回波的极化散射特性呈时变的特点,增大了目标识别难度,从而达到对抗雷达探测的目的.
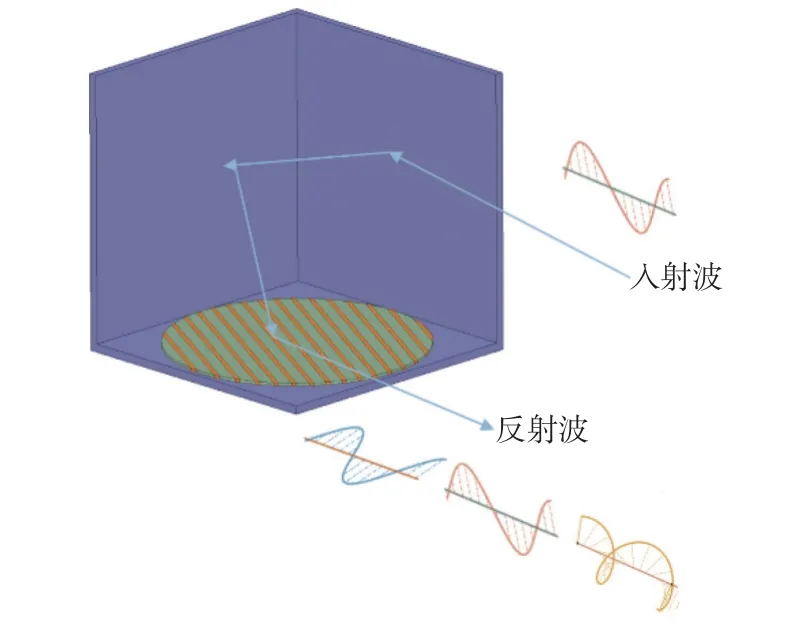
图3 变极化角反射器极化调控原理示意图Fig.3 Schematic of polarization control principle of the variable polarization corner reflector
此外,如果栅板的旋转速度足够快,角反射器可实现对雷达信号在脉冲内和脉冲间联合变极化调制;而对于常见的雷达信号脉宽和占空比而言,可实现脉冲间的变极化调制.
2 变极化角反射器散射特性分析
2.1 变极化角反射器参数优化
根据变极化角反射器设计理论,影响角反射器极化响应的主要有极化栅的结构参数、栅条旋转角度以及极化栅与角反射器反射面的相对位置等.
极化栅的结构参数主要包括极化栅半径、栅条厚度、栅条宽度、栅条稀疏度等.根据公式(5)可知,极化栅栅条之间的距离决定了垂直极化分量与水平极化分量之间的相位差,是影响极化栅极化调控能力的关键结构参数.在此,以栅条间距为例,考虑极化栅栅条均匀排布与非均匀排布两种排布方式,对极化栅结构参数的优化方法进行说明.
首先,考虑极化栅栅条均匀排布,通过设置栅条间隔d依次为2、6、10 mm,利用电磁仿真软件HFSS 模拟电磁波照射变极化角反射器,并经变极化角反射器调制后反射回自由空间的过程,计算得到单站散射回波.仿真参数设置如表1 所示.

表1 变极化角反射器电磁仿真参数设置Tab.1 Electromagnetic simulation parameter setting of the polarization variable corner reflector
图4 展示了金属栅条间隔依次设置为2、6、10 mm 时,经变极化角反射器调制后回波的总散射场、主极化分量、交叉极化分量以及两极化分量之间的相位差随极化栅旋转角度的变化趋势.

图4 栅条间隔对角反射器极化散射特性的影响Fig.4 The influence of polarization grid sparsity on polarization scattering characteristics
对比图4 三幅图中垂直极化分量和水平极化分量幅度值的相对大小以及两极化分量之间相位差的变化趋势可以发现,栅条间隔较小时,回波以垂直极化为主,且仅当极化栅旋转角度在60°以内时两极化分量之间相位差呈变化趋势,但差值不超过100°,变化范围较小.由此可见,栅条分布较密时,极化栅带来的变极化效果不显著.当栅条间隔取6 mm 时,占主导地位的极化分量对应的极化状态随旋转角度的改变发生多次变化,且两极化分量之间相位差的变化幅度接近360°,变化趋势平稳.当栅条间隔取10 mm 时,占主导地位的极化分量多次发生变化,但极化分量之间的相位差变化幅度不足200°,在一定程度上限制了极化状态的丰富度.综上分析,极化栅栅条间隔设定为6 mm 是相对较优解.
根据电磁波极化表征理论,将电磁波的垂直极化分量EHi和水平极化分量EVi通过Poincaré球表征,每种极化状态均可利用Poincaré球上的一点唯一表示[6].图5 给出了极化栅栅条间隔为6 mm 时,变极化角反射器的极化响应,其中LC 表示左旋圆极化,RC 表示右旋圆极化.由图5 可知,当极化栅转动时,经极化角反射器调制,反射后的电磁波的极化状态在Poincaré球上呈近似“8”字形分布,分别经历垂直极化、右旋椭圆极化、水平极化,右旋椭圆极化等多种极化状态,表明所设计的变极化角反射器实现了对电磁波极化状态的改变.
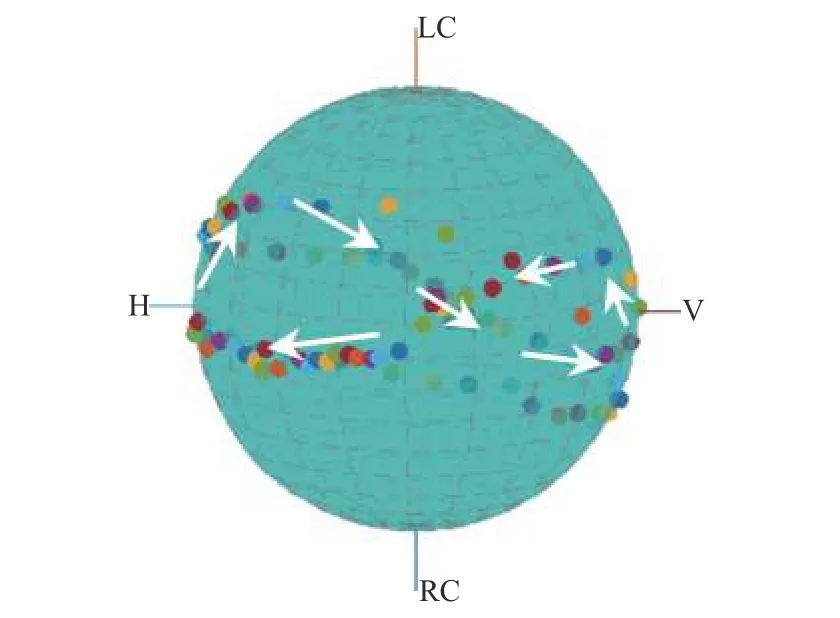
图5 变极化角反射器极化响应在Poincaré球上的表示(极化栅栅条均匀排布,d=6 mm)Fig.5 Polarization response to rotation represented with Poincaré sphere (with uniformly arranged polarization grid,d=6 mm)
此外,分析极化栅栅条非均匀排布情况下的极化调控能力,分别考虑栅条间隔由中心向边缘逐渐增大、栅条间隔由中心向边缘逐渐减小、栅条间隔随机排布三种排布方式,如图6 所示,三种极化栅调制后散射回波的极化响应由图7 给出.

图6 极化栅栅条非等间隔分布示意图Fig.6 Schematic of unequal spacing distribution of polarization grid strips
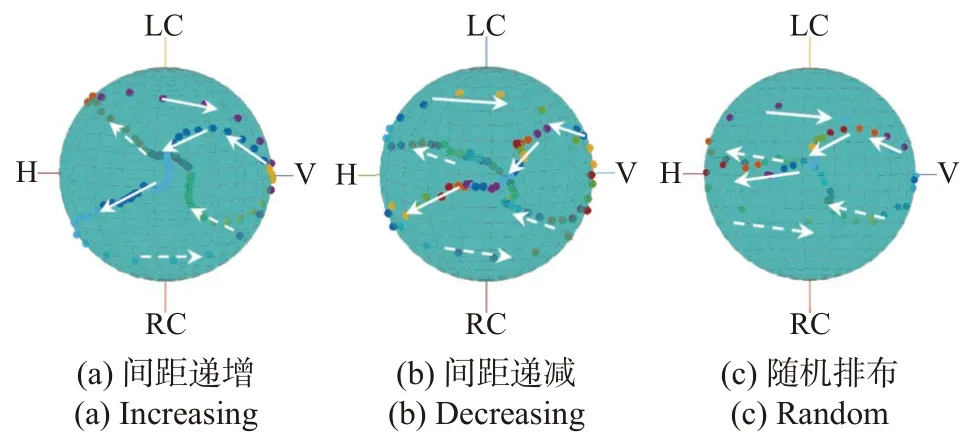
图7 变极化角反射器极化响应在Poincaré球上的表示(极化栅栅条非均匀排布)Fig.7 Polarization response to rotation represented with Poincaré sphere (with unequal spacing distribution)
图7 表明,极化栅非均匀排布可以提升极化状态分布的离散程度,对提升极化状态调控能力具有一定增益.同时,与均匀排布时的极化响应对比可知,非均匀排布增加了极化状态变化的无序性,给极化精准调控增加了难度.
除对极化栅栅条间隔的变极化效应进行分析之外,我们还仿真分析了极化栅栅条宽度、极化栅半径等结构参数对变极化角反射器极化调制效果的影响,分析表明极化栅栅条宽度的变化对极化调制效果无影响;极化栅栅板半径较小时调制效果较弱,随着栅板面积的增大,对金属角反射器的覆盖率增大,调制效果得到提升.
2.2 典型旋转角度下空域散射特性分析
为考察经变极化角反射器调制后的散射回波在口径面内的分布情况,选取极化栅旋转0°(极化栅栅条与x轴平行)以及60°(极化栅栅条与x轴夹角为60°)两个典型角度进行仿真分析,角反射器口面内散射场的幅度和相位分布分别如图8、图9 所示.与传统角反射器的极化散射特性(见图1)相比,变极化角反射器的交叉极化分量有明显提升,说明电磁波经过极化栅后,主极化和交叉极化分量的幅度被调制.从图8 和图9 的相位分布图可知,在反射器口面内,相位呈现区域性差异.为进一步分析变极化角反射器对不同方位角度入射波的调制效果,仿真计算了典型俯仰角下垂直极化分量和水平极化分量在方位向的分布变化趋势,如图10 和图11 所示.
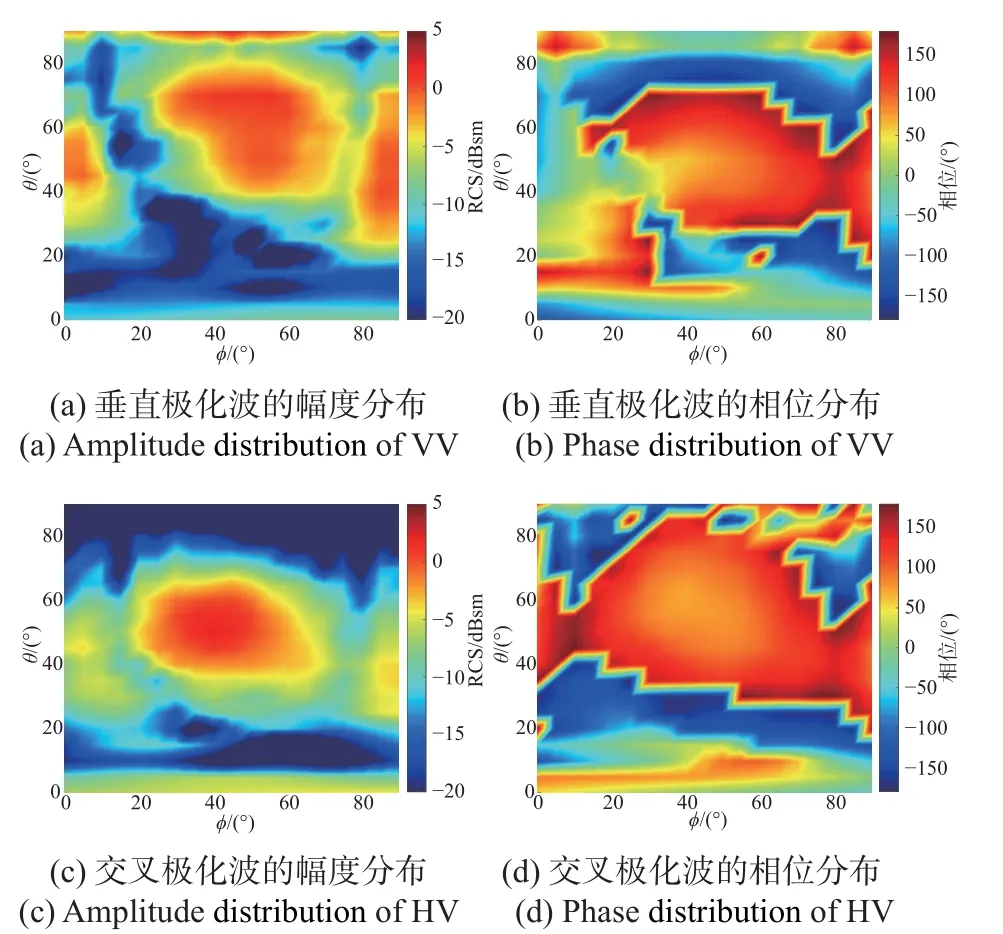
图8 极化栅旋转角度Ω=0◦时散射回波空域分布Fig.8 Spatial distribution of scattering echo with the rotation of polarization gate as Ω=0°
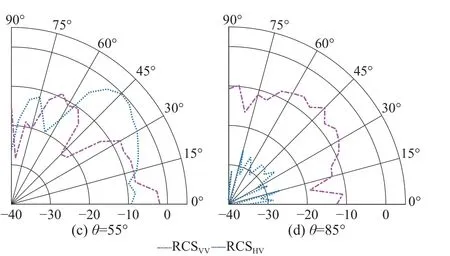
图11 极化栅旋转角Ω=60◦时典型俯仰角度单站RCS 分布Fig.11 Monostatic RCS distribution with typical elevations with the rotation of polarization grid Ω= 60°
由图10 和图11 可见:对于低仰角(θ=5°)入射波,不同极化分量在水平面内变化较平缓;对于高仰角(θ=85°)入射波,经调制后极化状态不发生变化,仍以垂直极化为主,在介于两者之间的角度上,两极化分量在水平面内呈现出明显的起伏趋势.上述分析说明变极化角反射器在口面内具备极化调控能力.
2.3 实验验证
为验证所提变极化角反射器对电磁波的极化调控能力,使用PCB 工艺加工了一副极化栅,极化栅栅条等间隔排布,结构参数与仿真参数保持一致.在栅板中心位置和金属角反射器底面的中心位置分别打孔,通过小型电机将极化栅与角反射器相连,栅板结构在电机的驱动下产生旋转,构成变极化角反射器.
实验依托微波暗室的RCS 采集系统开展,图12为实验场景图,转台位于暗室的正中心位置,以降低环境杂波的影响,将极化角反射器至于转台上,通过转动转台来改变入射波与变极化角反射器之间方位向的夹角.距离转台直线距离16 m 处分别安置一对X 波段线极化喇叭天线作为收发装置,两副喇叭天线紧邻,可作为单站使用,为避免相互影响,中间用吸波材料隔开.测试过程中,发射天线始终发射垂直极化波,通过旋转接收天线波导口的方向,使其依次接收散射回波的垂直极化分量和水平极化分量.
利用矢网分析仪依次采集定标金属球和变极化角反射器的回波数据,记为S21a、S21b并保存,为保证数据的可靠性,所有测试数据均取自静区.根据公式(6)计算得到变极化角反射器的RCS 值:
图13 至图15 给出了极化栅在三种不同旋转角度下,主极化和交叉极化分量在方位向的分布曲线.
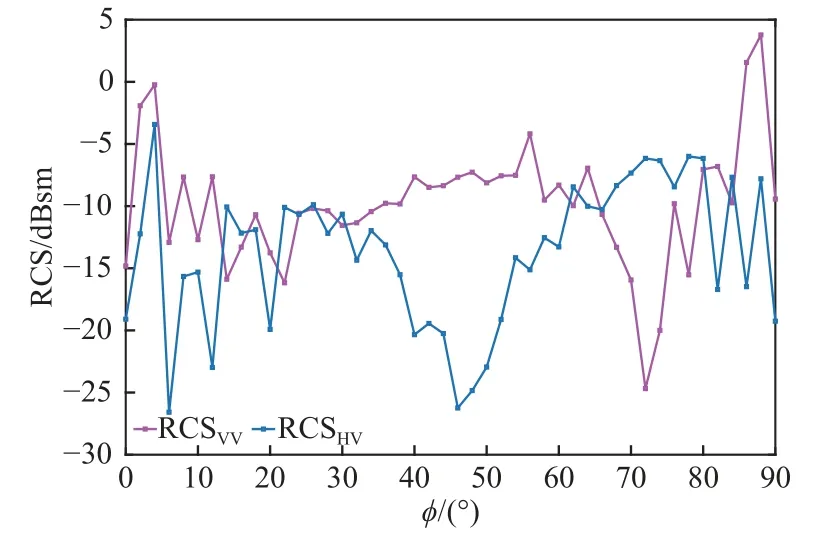
图13 极化栅与入射波垂直时单站RCS 方位向分布Fig.13 The distribution of monostatic RCS in azimuth with the polarization grids parallel to the incident wave

图14 极化栅与入射波夹角为45°时单站RCS 方位向分布Fig.14 The distribution of monostatic RCS in azimuth when the included angle between the polarization grid and the incident wave equals to 45°

图15 极化栅与入射波平行时单站RCS 方位向分布Fig.15 The distribution of monostatic RCS in azimuth with the polarization grids perpendicular to the incident wave
由图13 至图15 可见:随着入射波方向的改变,散射回波的能量在水平方向呈起伏变化趋势;当极化栅栅条与角反射器之间的夹角发生变化时,主极化与交叉极化分量的相对大小发生改变,即占主导地位的极化分量在垂直极化与水平极化之间更迭,相应地,回波极化状态发生改变.
本实验开展过程中,由于喇叭天线的俯仰和方位不可调整,同时考虑高空架设的安全问题,仅对较低仰角(θ=25°)入射波照射角反射器的场景进行了测试,一定程度上导致了测试得到的回波能量较低.但从实验结果上来看,即使在较低仰角下,散射回波的极化状态随方位变化、极化栅旋转呈现变化趋势,验证了变极化角反射器具有较强的极化调控能力.
3 结 论
本文面向雷达对抗应用场景中的无源干扰发展需求,充分利用极化栅与角反射器的优势,将极化栅与传统三面角反射器结合,提出了一种低成本、极化状态可调的新型角反射器结构,通过旋转极化栅,可以实现对雷达回波极化状态的实时调控.文章重点分析了极化栅的栅条间隔以及旋转角度对极化调控能力的影响,当极化栅旋转时,回波的极化状态在Poincaré球上呈近似“8”字形.针对典型旋转角度,分析了经变极化角反射器调制后雷达回波的空域散射特性,结合典型俯仰角下的单站RCS,探索了角反射器口径面内的极化响应.最后,加工制作了极化栅,对变极化角反射器的散射特性进行了实验测试,验证了变极化角反射器具备较强的极化调控能力.本文所设计的变极化角反射器为极化信息应用于目标防护提供了新方向,所提出的研究方法和设计思路对新型角反射器的研究提供了新思路.本文工作侧重于阐述变极化角反射器的变极化效果,后续可在此基础上对极化状态的精确控制以及对雷达成像、跟踪检测的干扰效果开展相关研究工作.

