基于绕射场修正快速迭代物理光学法的海面舰船与角反阵列电磁散射分析
丛洲 丁大志 樊振宏 何姿 谷继红
(南京理工大学, 南京 210094)
0 引 言
随着我国经济快速发展和对外开放不断扩大,国家战略利益和战略空间不断向海洋拓展和延伸,迫切需要发展海洋国防力量,增强海上目标态势感知能力与反电子侦察能力,提高我国海洋信息获取武器装备的现代化水平.其中,海战场中使用的无源角反射器是舰船目标在进行雷达电子对抗时常采用的一种重要的无源干扰装备[1].由于无源反射器不需要供电系统,也不会像雷达、天线一样产生电磁波,而当电磁波入射到角反射器上时,角反射器将入射波沿入射方向反射回去,具有较大的雷达散射截面积(radar cross section,RCS),且组合使用可形成与真实目标相似的假目标,降低了雷达的检测、识别和跟踪性能[2-3].
目前,针对海面目标电磁散射分析的研究工作已经取得了一定的收获,国外的R.J.Burkholder 等结合迭代物理光学(iterative physical optics, IPO)方法和蒙特卡罗(Monte Carlo)方法研究了随机粗糙海面与简化二维和三维舰船目标的复合电磁散射问题[4];M.R.Pino 等提出的广义前后向法(generalized forwardbackward method, GFBM)结合传统的矩量法(method of moments, MoM)[5],可以处理海面上复杂目标的散射问题.国内的复旦大学金亚秋院士团队利用GFBM 实现了低掠角入射时一维动态分形粗糙面和二维舰船目标的双站散射模拟[6-7];西安电子科技大学郭立新等研究了物理光学近似法,以及时频域数值混合算法,分析了目标与粗糙面复合散射问题[8].对复杂的无源角反干扰目标的电磁仿真而言,目前国内外开展的仿真方法研究较为单一,最初只是通过计算角反射器的有效面积来分析其散射强度.之后,1998 年赵维江等利用区域投影法分析了角反射器的散射截面积[9].2007 年陈振华等利用时域有限差分(finite-difference time-domain, FDTD)法计算了三面角角反射器的电磁散射特性,得到在不同波长和不同入射角度时角反射器RCS 值及其散射的波瓣方向图[10].2010 年张婷等利用MoM 对单个角反射器的雷达散射进行了研究[11],在计算过程中结合多层快速算法,提高了计算速度,从工程应用的角度考虑了角反射器在实际应用过程中的角度误差、入射波角度变化对角反射器RCS 的影响.2018 年梁美彦等利用频率步进法研究了太赫兹波段下角反射器的散射特性[12].但是,实际的海战场环境中,海面、舰船、角反射器的电磁散射特性是相互依存、相互影响的,并且在实际战场环境中的角反干扰大都以角反射器阵列的形式存在,目前研究者们报导的文章多集中在只针对单个角反的平均散射强度的分析,较少会考虑海面目标与角反之间的耦合、角反射器阵列与海面之间的耦合磁散射的精确计算.
本文以电流IPO 快速方法为手段,在考虑表面电流的散射贡献基础上加入边缘绕射场的耦合影响作用,研究了海面+舰船+角反阵列一体化的电磁计算快速方法,通过对一体化的高效建模,为分析角反阵列对舰船目标的反电子侦察的干扰效果提供了有效的仿真手段.
1 局部电流IPO 方法
1.1 海面目标电流迭代散射场求解
IPO 法由F.Obelleiro-Basteiro 等在1995 年初次提出[13].该方法通过不断更新表面电磁流,模拟了电磁波在目标内部的多次反射过程,物理过程清晰,程序实现简单,无需对矩阵进行求逆运算,精度较高.对于目标与海面的耦合散射场求解问题而言,金属目标(舰船、角反)与海面是相互耦合的散射体,其相互作用的电磁散射计算过程可以采用图1 所示状态来描述:Case1 为介质粗糙面初始感应电流引起的散射和目标初始感应电流引起的散射;Case2 为目标与介质粗糙面初始感应电流分别在目标表面引起的二次耦合辐射场;Case3 为目标与介质粗糙面初始感应电流分别在介质粗糙面引起的二次耦合辐射场;Case4 为目标与介质粗糙面相互作用激发的高次散射回波.
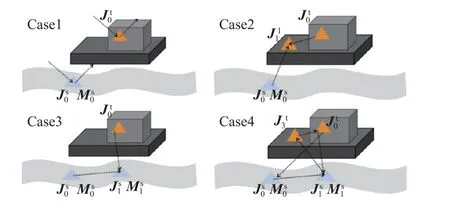
图1 金属目标与海面的电磁散射作用Fig.1 Electromagnetic scattering between metal target and sea surface
首先入射波直接照射到目标和粗糙面所产生的一阶感应电磁流可以写为(上标为t的是金属目标上的电流,上标为s的是海面上的电磁流):
式中:海面总的二阶入射电场和磁场为
最后,按照以上的规律进行重复迭代,不断更新目标和粗糙面的感应电磁流,直至满足精度要求.通过此方法的迭代可以充分考虑到目标与粗糙面之间的耦合效应.在远场近似条件下[14],可以得到复合模型的远区总散射场:
1.2 改进的海面目标局部耦合迭代理论
在使用IPO 的过程中,反射场在每次迭代中通过前一次迭代的感应电流的辐射积分来求解.反过来,反射场对作为新的辐射源再对表面感应电流进行校正.因此,电流迭代次数等于物体内部反射的次数[15].本文对迭代方式进行了改进,使用反射次数追踪方法来记录网格表面每个区域的反射次数.因此省去了多余的迭代循环次数,减少了因为多次重复迭代所消耗的计算时间,从而提高了迭代求解的效率.同时,本文对全局电流迭代耦合求解的IPO 方法提出了局部电流迭代求解的改进方案,在电流迭代耦合交互作用的过程中,将全局电流耦合替换为局部电流耦合,以减少目标的未知量.改进的方案如下:
1.2.1 海面近场截断理论
海面上表面电流的的迭代耦合作用求解可以分为近场区域和远场区域的相互作用,但实际上,对于粗糙海面而言,只有局部区域的迭代占主导作用,特别是近似平坦的粗糙面[16].粗糙面上的辐射场随着格林函数中场点和源点之间距离r的增加而减小.当大于一定阈值时,认为粗糙面面元之间的耦合效应接近于0.在实际仿真中,将海面迭代的局部区域设置为20 个波长范围,即距离场点20λ 外的海面面元不记入计算.如图2 所示,假设rfield和rsource分别是粗糙表面上的场点和源点,当它们的距离|rfield−rsource|>20λ时忽略它们之间的相互作用.这被称为海面的局部内迭代.
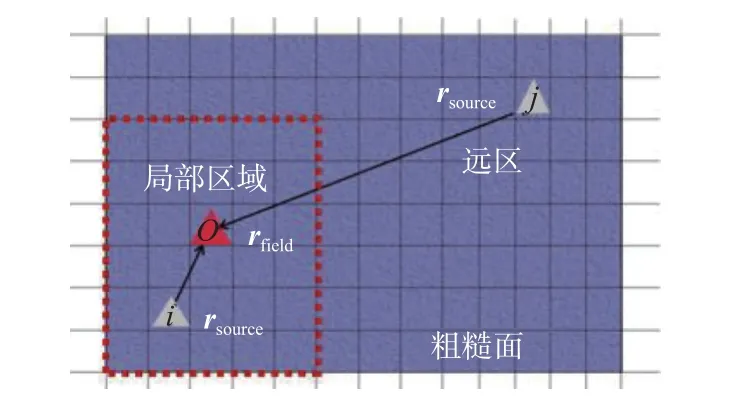
图2 粗糙面上局部相互作用区域的说明Fig.2 Explanation of the local interaction area on rough surfaces
1.2.2 海面与目标镜面耦合区域截断理论
对于海面和目标之间的耦合效应,称为外迭代.计算粗糙表面与物体之间相互电磁耦合作用时,由于海面未知数较大,计算外迭代过程占据了大部分的计算时间.当源点与场点距离足够远时忽略物体与海面之间的电磁耦合效应,利用粗糙表面散射的镜面反射特性来减小粗糙表面的耦合面积.该特性表明,主要散射能量集中在镜面方向.因此,可以根据镜面反射截断粗糙表面上的耦合区域.
如图3 所示,截断区域的大小和入射波的方向以及物体尺寸有关.粗糙表面截断区域的计算公式如下:
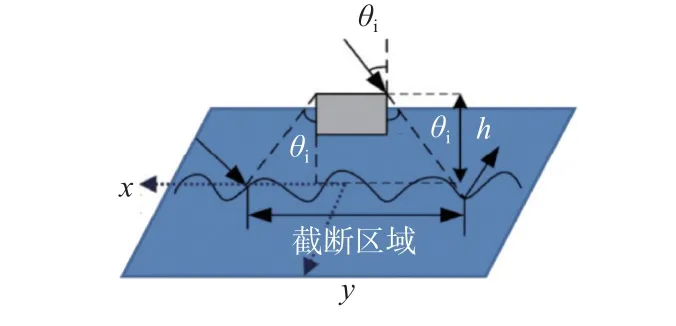
图3 粗糙面与目标耦合区域Fig.3 Coupling region between rough surface and target
式中:x和y分别为截断区域的x方向和y方向的离坐标原点的距离;和分别为粗糙面上目标x方向和y方向的最小和最大距离; θi为入射角度;h为目标的高度.
1.2.3 海面与目标耦合区域局部耦合理论
最后,在海面截断的基础上,引入射线追踪机制,如图4(a)和(b)所示,图中一条射线的轨迹是AB-C,对于目标上C点而言,只计算B点周围红色虚线内海面面元对它的耦合效应,红色区域的大小为15~20 个波长.同样,对于海面上的三角形,也用此方法计算目标上的三角形对截断海面的耦合效应.值得注意的是,通过射线追踪没有找到上一次相交面元(即射线只在自身弹跳一次)的三角形不用此方法计算,仍然采用传统的IPO 方法计算.
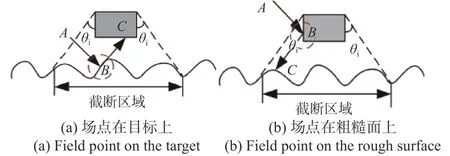
图4 海面与目标耦合区域不同位置的迭代区域选择Fig.4 Selection of iteration areas at different positions in the coupling region between sea surface and target
2 快速局部IPO 方法
局部IPO 方法获取相对精确散射场计算结果的同时,减轻了对大未知量循环嵌套下对计算时间的巨大需求.为了进一步提高计算效率,在该方法的基础上利用快速多极子方法(fast multipole method,FMM)[17]对耦合场积分过程进行加速,并基于GPU图像处理器平台实现算法的高度并行计算.
2.1 FMM 方法加速
FMM 主要原理是将目标用均匀的小正方体分为许多组,每两个组之间的耦合根据它们所在的位置分为两种计算方式.当它们是相邻组时,采用常规IPO 方法进行计算;而当它们是非相邻组即远场组时,则采用聚合-转移-配置方法计算.
本文方法中,目标表面上的N个散射面元都是一个散射中心即一个单极子,计算复杂度为O(N2);而应用FMM,任意两个子散射体的耦合可以由它们所在组的组中心建立联系,每个组中心是一个多极子,其计算复杂度为O(N1.5).在所要研究的海面目标耦合散射求解问题中,两元素的聚合、转移、配置示意如图5 所示.
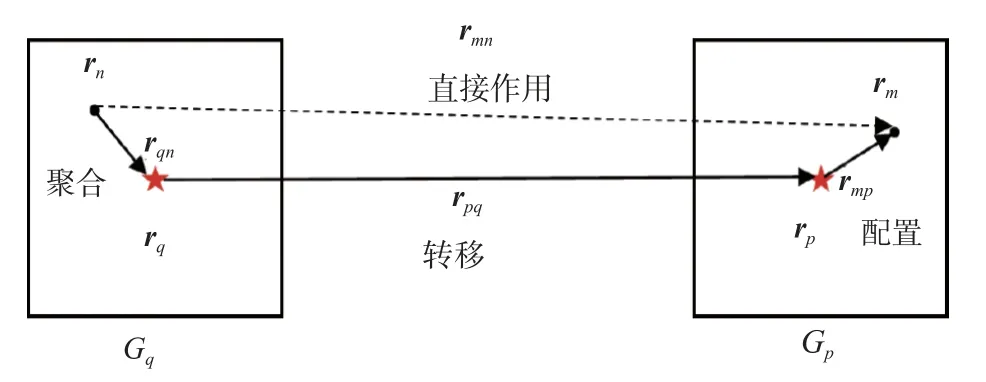
图5 FMM 两元素聚合、转移、配置示意图Fig.5 Schematic of FMM for aggregation, transfer and configuration of two elements
图5 中,rm和rn分别是场点与源点,rp和rq是场组Gp和源组Gq所表示的立方体的中心点.它们之间满足如下的关系:
当场组Gp和源组Gq满足远区组条件即时,标量格林函数的梯度和并矢格林函数在角谱空间的表达式可以写成:
至此,可以将格林函数的角谱展开式代入到计算粗糙面与目标复合散射的IPO 方法中,得到:
最后,根据反射次数迭代更新粗糙面与目标表面的感应电磁流,代入远场近似公式中可以求出远区总散射场.
2.2 GPU 并行
对目标进行局部耦合的IPO 方法迭代求解时,因为每个面元的迭代过程是互不干扰的,所以对局部耦合的IPO 方法的并行实际上就是对目标每个离散面元的并行.将GPU 并行的方法运用到本文计算中,有以下四个步骤:
1)在CPU 端读取模型的数据(包括三角形编号、节点编号、节点坐标等)并进行预处理,对目标进行八叉树分组,进行面元的亮暗区判断、初始感应电磁流的求解.
2)将第1 步骤中处理好的面元信息传输到GPU 端,在GPU 端对每个离散面元进行并行,迭代求解最终收敛的耦合感应电磁流.
3)将GPU 中每个离散面元上的感应电磁流信息传输到CPU 端,在CPU 端对每个独立面元进行初始电磁流与耦合感应电磁流的累加和散射场的计算.
4)累加每一个离散面元的散射场从而得到最终的总的散射场.
总的流程图如图6 所示.
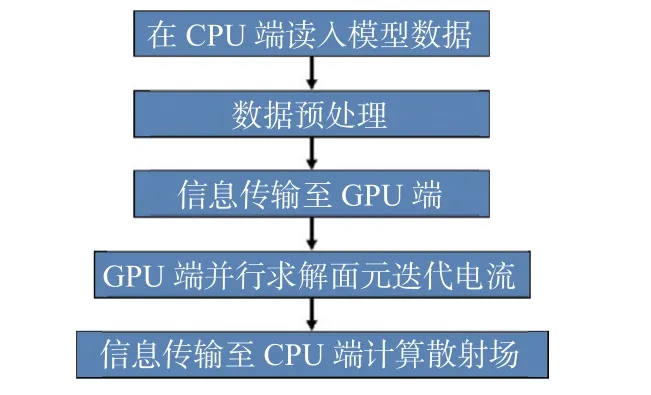
图6 IPO 方法的GPU 并行流程图Fig.6 GPU parallel process flowchart of the IPO method
3 海面目标的绕射场修正
3.1 耦合绕射场修正
由于海面目标存在大量的棱边绕射场影响着目标的散射特性,因此需要在IPO 的表面感应电流积分求解散射场的基础上,利用一致性绕射理论(uniform theory of diffraction, UTD)方法[18]计算出棱边的绕射场:
同时,对于绕射射线形成的射线场,可作为新入射源Ei(Q)对目标表面电流产生的散射场进行修正,Q对应目标上的棱边.如图7 所示,计算反射+绕射场,将凯勒锥面上的衍射光线进行等角度的分裂,作为新的入射光线,在目标上进行新的射线跟踪.通过分裂的绕射射线产生新的耦合场对目标的表面进行辐射并产生修正的散射场.经过修正的总散射场为
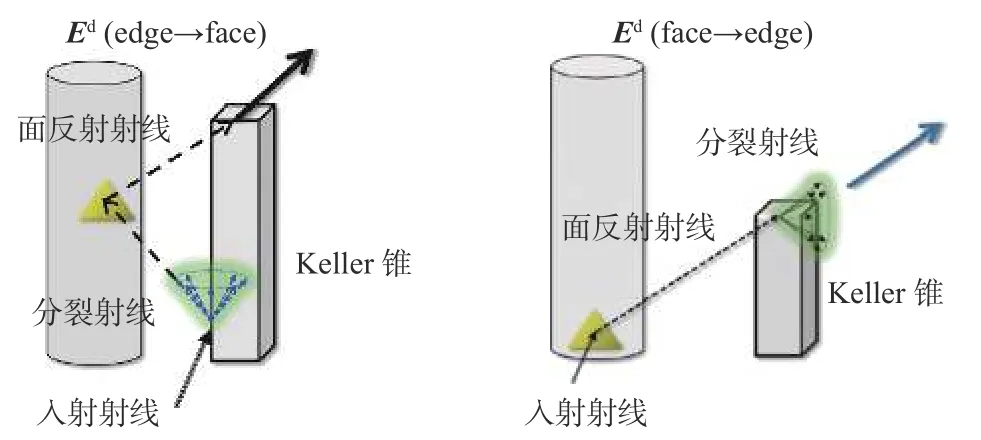
图7 绕射场分裂后对面元进行再辐射作用Fig.7 Re-radiation of the split diffraction field on the target Surface
3.2 海面+舰船+角反阵列一体化散射模型
通过快速IPO 方法与耦合绕射场修正,可以对大场景的海上目标进行高效的电磁散射特性分析,将无源干扰角反射器阵列与海面和目标之间的影响作用进行高效的求解.基于本文提出的绕射场耦合的快速IPO 方法实现RCS 的高效计算,总的散射公式为
一体化的海面+舰船+角反阵列的散射模型如图8所示.
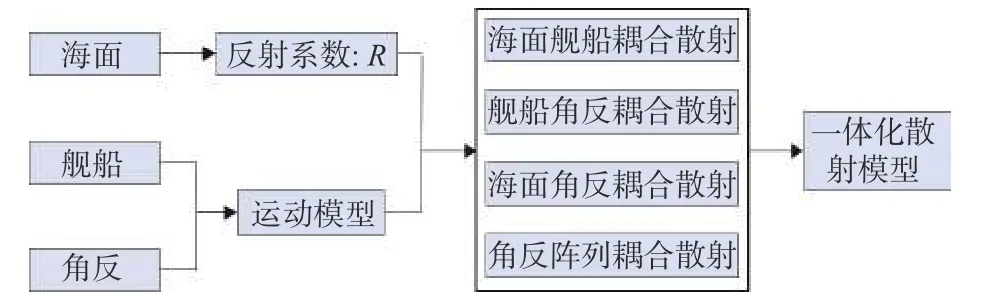
图8 海面角反舰船一体化散射模型图Fig.8 Integrated scattering model of sea surface and ship
4 海面+舰船+角反RCS 快速计算
4.1 三面角反射器的局部IPO 方法仿真
为了证明本文方法在计算多次反射结构上的优势所在,对典型的反射器模型进行了RCS 仿真计算.如图9 所示的金属三面角反射器模型,每边长为2 m,在入射频率为3 GHz 的平面波入射角度为φ=0°,θ=45°的仿真条件下,分别使用精确数值方法分层FMM(multilevel FMM,MLFMM)和本文的局部IPO方法(本算例中未采用FMM 和GPU 加速)对目标的电磁散射特性进行分析计算.从图10 所示的电流耦合作用分布图可以看出,三面角上不同三角形面元上计算获得的目标表面其余面元对其产生的耦合场的作用大小有显著差别.
图9 三面角反射器结构Fig.9 Trihedral reflector structure
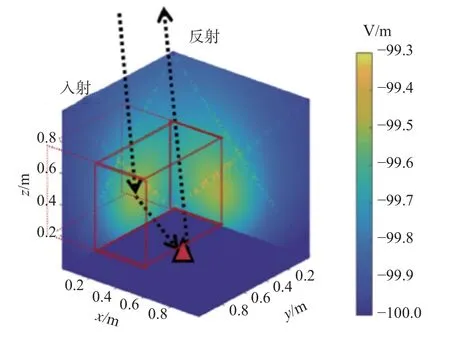
图10 三面角反射器结构电流互作用分布Fig.10 Current interaction distribution of trihedral reflector structure
图10 中电磁波在面元上反射的射线路径为图中黑色虚线所示,对于整体的三角形面元而言,在入射角度固定的情况下,在镜面反射路径上的面元是耦合作用最强的面元,并且其余面元的耦合强度从这个强点依次向周围区域减弱,证明了局部IPO 方法中的局部区耦合思想在含有多次反射的结构RCS 计算中的正确性.
接下来,在单站入射角为φ=45° ,θ=0°∼90°的情况下,将该角反射器模型的VV 极化单站RCS 的计算结果与MLFMM 的仿真结果进行对比.
从图11 可以看出,本文提出的局部IPO 方法在取边长为15 λ的正方体范围作为局部耦合区域时的仿真RCS 结果曲线与MLFMM 方法基本吻合.将MLFMM 计算结果作为标准值,在表1 中比较了局部IPO 方法与传统IPO 方法的计算时间和RCS 均方根误差.从误差对比上可以看出,局部IPO 的仿真精度比传统IPO 略低,但从仿真时间对比而言,局部IPO 方法比传统IPO 方法计算效率提高了83%.
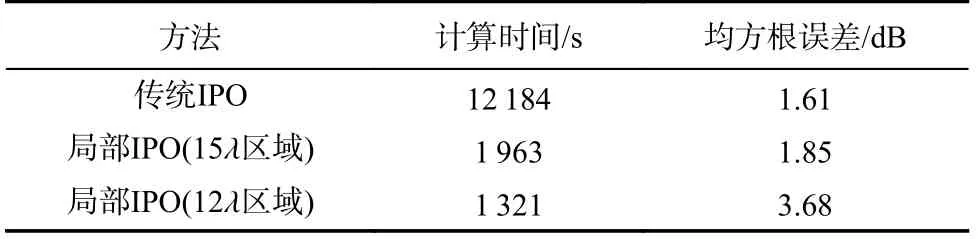
表1 局部IPO 方法与传统IPO 方法的计算时间和RCS 均方根误差Tab.1 Computation time and RMS error of RCS for local IPO method and traditional IPO method
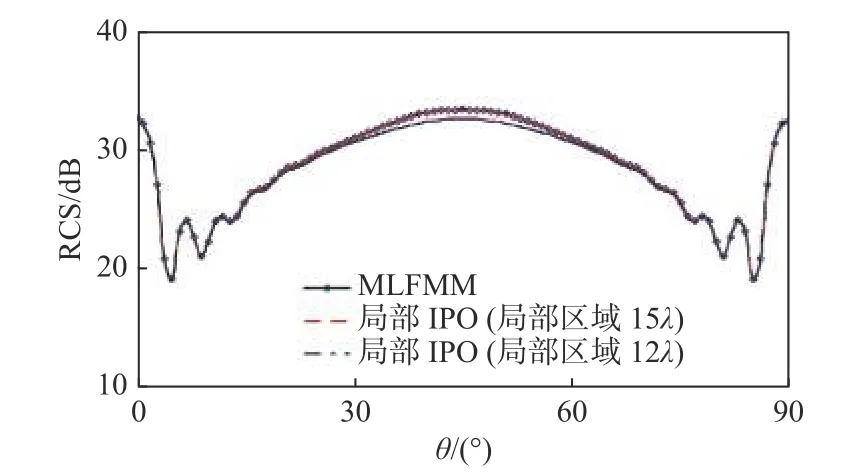
图11 三面角反射器结构VV 极化单站RCS 计算结果Fig.11 Monoststic RCS results of trihedral reflector structure in VV polarization
4.2 棱边结构的绕射场修正
当目标包含大量的棱边结构时,需要考虑棱边绕射场对总散射场的影响,仿真了如图12 所示的四个理想电导体(perfect electric conductor,PEC)金属平板模型,分别在考虑绕射作用和不考虑绕射作用的前提下,计算得到的双站RCS 结果如图13 所示.本算例仿真的双站入射角为φ=90° ,θ=135°,频率为3 GHz.本文中的绕射射线是在棱边的凯勒(Keller)锥方向上等比例分裂得到的,如图14 所示,通过控制绕射射线分裂的数量来提高绕射场耦合贡献的占比,本模型有82 704 个网格三角形和1 605 条边.这里我们将基于电场积分方程(electric field integral equation, EFIE)计算的MLFMM 方法作为精确结果进行了误差的对比,从图15 可以看出,在不考虑绕射场耦合时RCS 误差约为6.3 dB,考虑耦合绕射情况下的RCS 误差约为4.1 dB.显然,增加新射线的数量会得到更高的精度,但同时计算时间也随之增加.
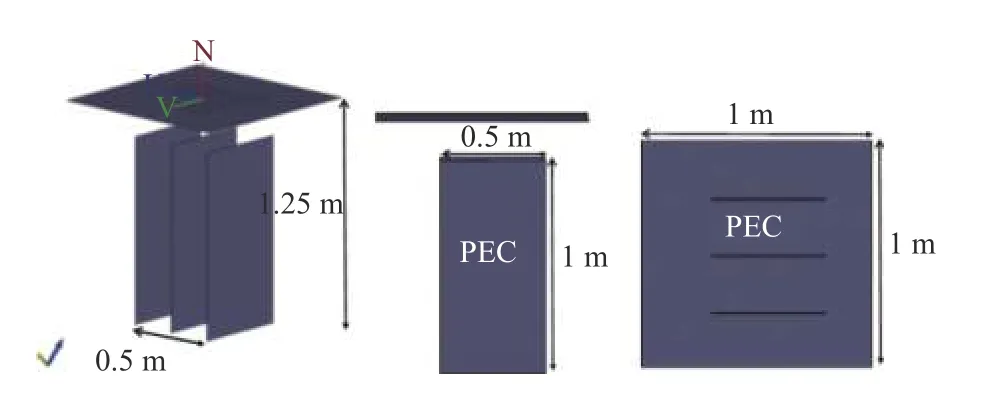
图12 四个金属平板模型Fig.12 Four metal plate models
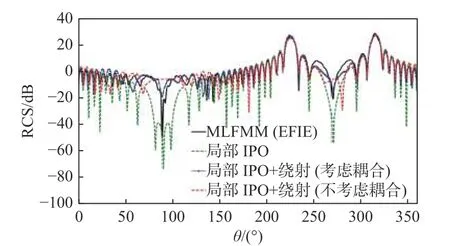
图13 四个金属平板模型的双站RCS 计算结果Fig.13 Bistatic RCS results for four metal plate models
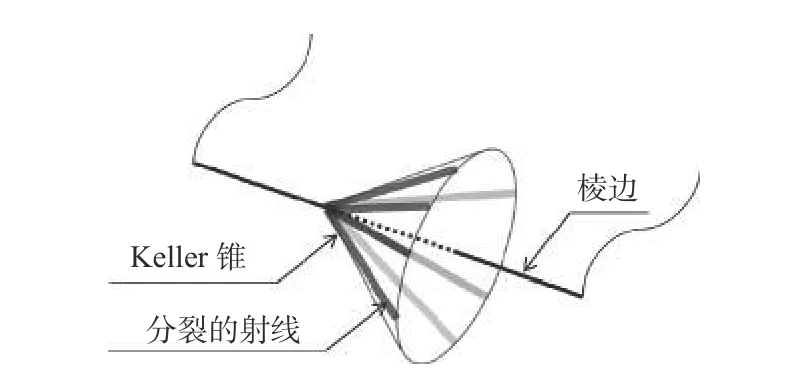
图14 绕射射线在Keller 锥上分裂的示意图Fig.14 Splitting of diffraction rays on the Keller cone
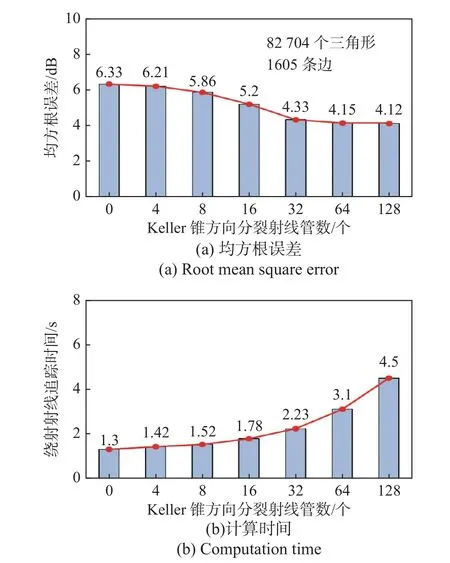
图15 误差和计算时间随绕射射线分裂数量的变化曲线Fig.15 Error and computation time vs.the number of diffraction rays
4.3 二十面体角反射器RCS 仿真
在实际的海面战场环境中,二十面体的角反射器被广泛应用,本文采用FMM 和GPU 加速的局部IPO 方法(快速IPO)对如图16 所示的二十面体的角反射器进行RCS 仿真分析,入射波频率为3 GHz 的计算结果如图17 所示.二十面体反射器模型三角形边长为1.4 m.单站入射角为φ=45° ,θ=0°∼90°.与普通模型不同的是,二十面体角反的棱边结构较多,因此更加需要评估绕射场对总场的影响.从表2 误差对比的结果可以看出,当使用绕射场修正目标总场时,获得的RCS 精度更高.
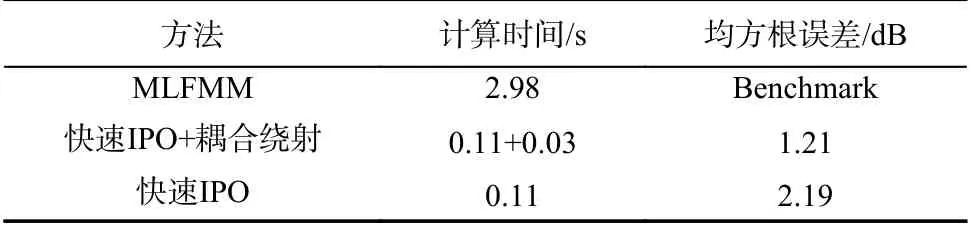
表2 考虑绕射与否快速IPO 方法的计算时间和RCS 均方根误差Tab.2 Computation time and RMS of RCS for fast IPO method with and without considering diffraction
图16 二十面体角反射器结构Fig.16 Icosahedron reflector structure
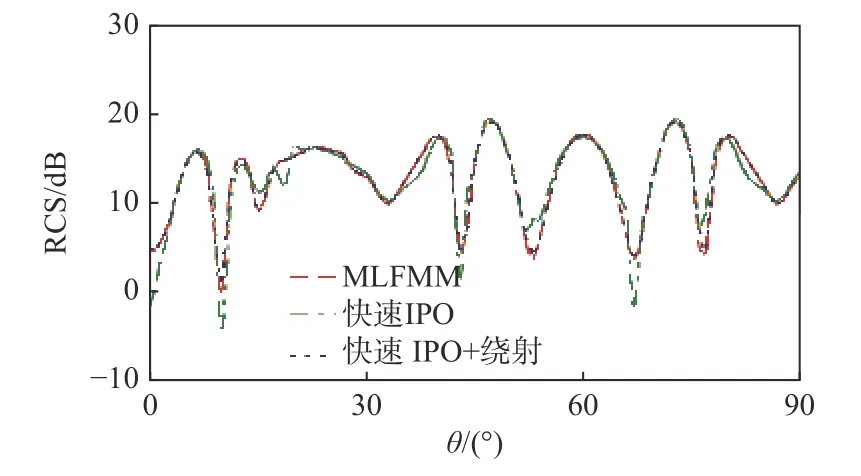
图17 二十面体角反射器结构单站RCS 计算结果Fig.17 Monostatic RCS results of icosahedron reflector structure
同时,采用快速IPO+绕射方法仿真如图18 所示的两个角反组成的阵列模型,给出考虑角反直接耦合作用和不考虑角反直接耦合作用的仿真结果,如图19 所示.
图18 组合二十面体角反射器Fig.18 Combined icosahedron reflectors
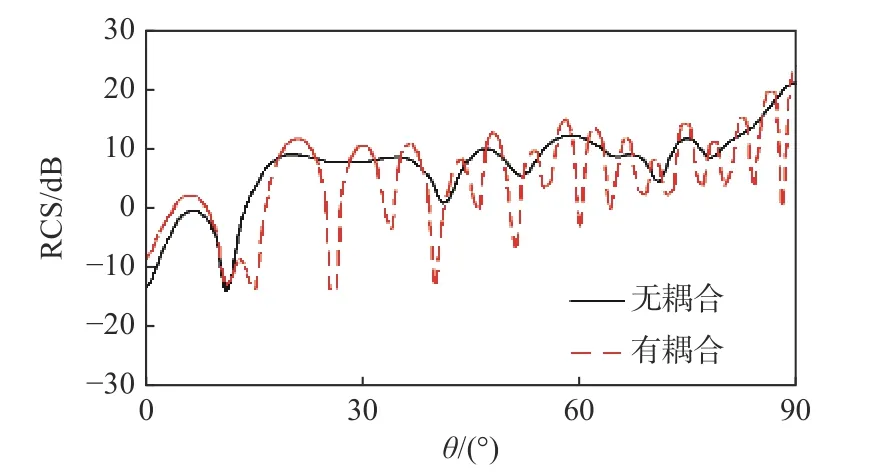
图19 组合二十面体角反射器双站RCS 计算结果Fig.19 Bistatic RCS results of combined icosahedron reflector
从图19 可以看出,对于角反射器模型而言,每个角反上都分布着多个类似三面角的多次反射结构,且每个多次反射结构之间会相互形成新的多次反射结构,导致目标的整体RCS 在不同观察角度下发生变化,因此,需要利用本文方法对角反直接的耦合进行精确计算,以保证角反阵列仿真的可靠性.
4.4 不同海情海面与角反射器RCS 仿真
对图20 所示不同海情下的一组二十面体角反阵列进行单站RCS 仿真,仿真频率为2 GHz,海面长为20 m,二十面体反射器模型三角形边长2.8 m.海面的均方根高度分别为0.5m、1m、2m.海上介电常数εr=(5.2+3.1j).在观察角度θ=0°~90°,ϕ=0°下RCS仿真结果如图21 所示.

图20 不同海情海面二十面体角反射器模型Fig.20 Icosahedron reflector model in different sea states
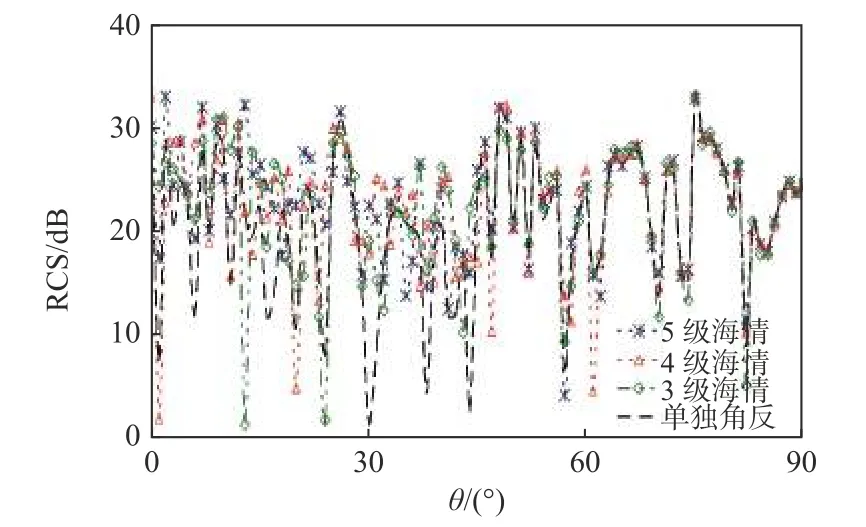
图21 不同海情海面二十面体角反射器模型单站RCS 仿真结果Fig.21 Monostatic RCS results of icosahedron reflector model in different sea states
从图21 可以看出,在小角度入射的情况下,海面对角反的RCS 影响较大.统计了角0°~30°入射时的RCS 均值,5 级海情下粗糙面与角反的RCS 均值为24.8 dB,4 级海情下为23 dB,3 级海情下为22.6 dB.可以看出海情越大,海面角反的RCS 均值越大.在大角度入射情况下,尤其是相对海面是小擦地角情况下,海面的散射对整体目标的影响较小.还可以看出,3 种海情的总散射场与单独角反模型的散射场相接近,这是因为角反的RCS 回波较大,而较小的海面散射的贡献不足以改变整体的RCS 值.
4.5 海面+舰船+角反射器RCS 仿真
针对海面舰船加角反阵列组合目标,更加需要考虑海面与目标之间、目标与角反之间的耦合作用,对如图22 所示的海面+舰船+角反阵列模型进行RCS 仿真,结果如图23 所示.海面由高斯谱生成,海面尺寸大小为40 m×8 m,海水在频率为3 GHz 下的相对介电常数εr=(55.9+37j),海面均方根高度为0.05 m,相关长度为0.6 m.在海面上,目标是一艘14 m×4 m×2 m 理想导体的船和边长为1.5 m 的3 个二十面体角反射器组成的角反阵列.总未知数2 587 119,其中海面未知数为1 843 200.入射波频率为3 GHz,入射角为θi=45°,φi=0°,观察角度为θs=−90°~90°,φs=0°,VV 极化.用FMM 和GPU方法加速的快速IPO+绕射方法计算复合模型的双站RCS,统计并比较不同算法的计算时间与误差,结果见表3.
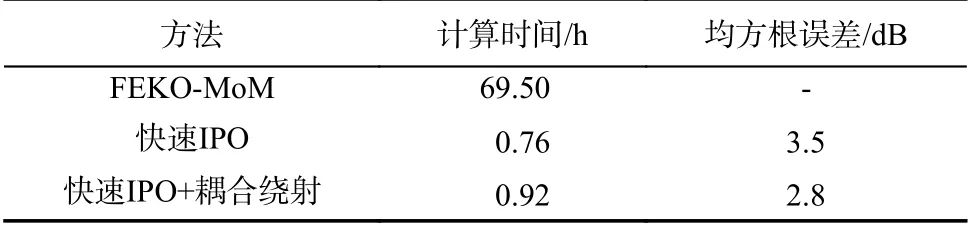
表3 考虑绕射与否快速IPO 方法的计算时间和RCS 均方根误差Tab.3 Computation time and RMS of RCS for fast IPO method with and without considering diffraction

图22 海面+舰船+角反的组合模型Fig.22 Combined model of sea surface + ship + corner reflector
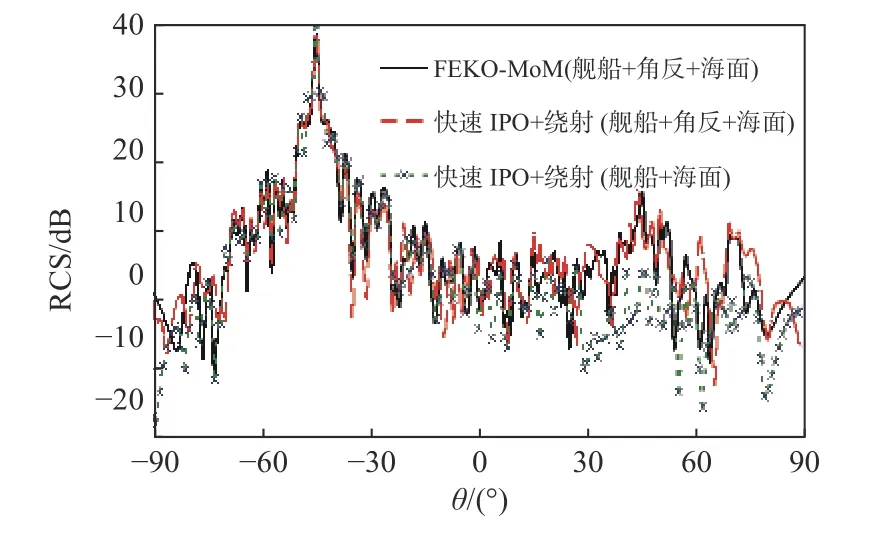
图23 海面+舰船+角反射器的组合模型双站RCS 计算结果Fig.23 Bistatic RCS results of combined model of sea surface+ ship + corner reflector
从表3 可以看出,本文方法相比于精确数值方法提高了约91 倍.同时,由于考虑了耦合绕射场的修正作用,计算精度有所提高,保证了仿真结果的可靠性.
4.6 不同海情海面+舰船+角反射器RCS 仿真
对图24 所示不同海情下的大场景海面+舰船+角反模型的单站RCS 进行仿真,海面尺寸大小为80 m×20 m,舰船模型尺寸26 m×8 m×4 m.海水在频率2 GHz 下的相对介电常数εr=(5.3+3.2j),海面的均方根高度分别为0.5 m、1 m、2 m.在观察角度θ=0°~90°,φ=0°下计算得到的单站RCS 结果如图25 所示.
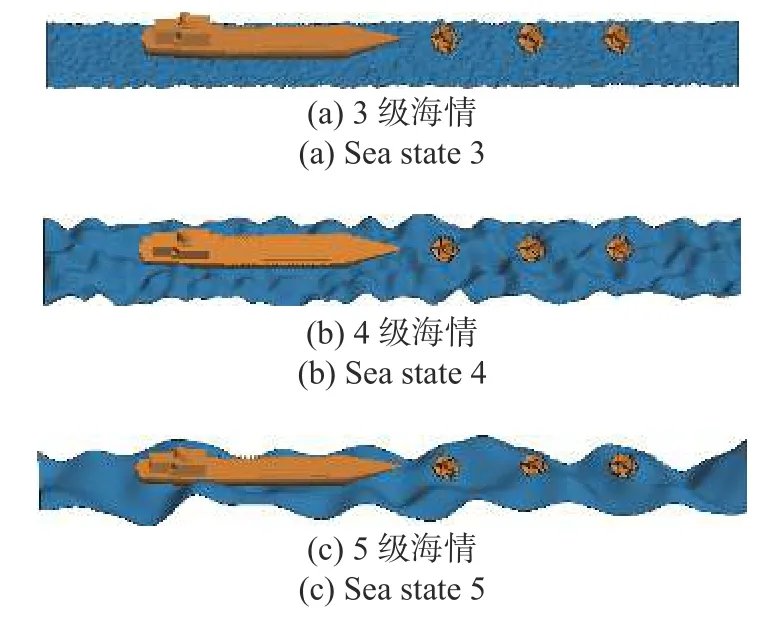
图24 不同海情海面+舰船+角反射器模型Fig.24 Model of sea surface+ship+corner reflctors in defferent sea states
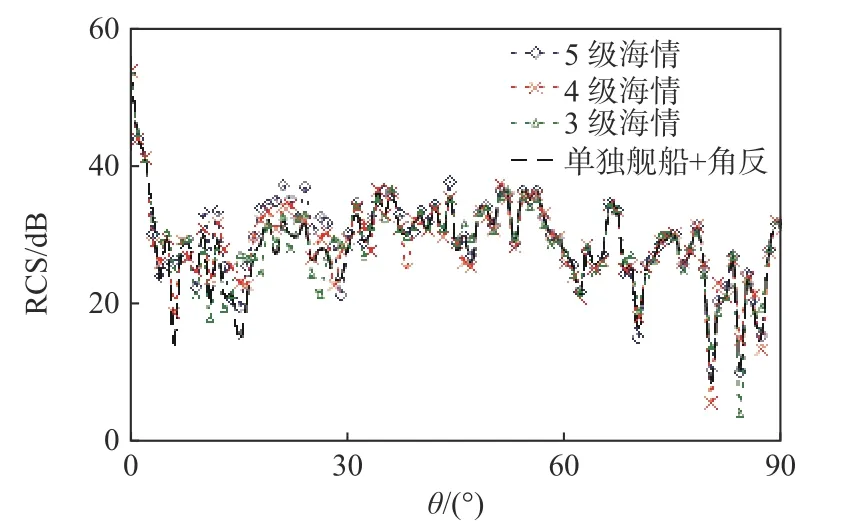
图25 不同海情海面+舰船+角反模型单站RCS 仿真结果Fig.25 Monostatic RCS of sea states + ship + corner reflectors model in different sea states
从图25 同样可以看出,在小角度入射的情况下,海面对舰船与角反组合的RCS 影响相对较大,但是没有海面角反组合情况下海面对角反的影响那么明显.还统计了0°~30°入射时的RCS 均值,5 级海情下粗糙面与角反舰船的RCS 均值为30.7 dB,4 级海情下粗糙面与角反舰船的RCS 均值为29.9 dB,3 级海情下粗糙面与角反舰船的RCS 均值为28.8 dB.同样在大角度入射情况下,尤其是相对海面是小擦地角情况下,海面的散射对整体目标的影响较小.
4.7 舰船一维像仿真与角反射器阵列模拟
利用本文的仿真方法对海上舰船目标一维距离像进行仿真,并尝试通过角反阵列的排布模拟目标的一维距离像.拖曳式角反射器阵列是舰船干扰雷达的重要手段.在信息化条件下的电子对抗中,雷达制导武器系统对于舰船构成重要威胁[19].为了对抗各种雷达制导导弹对舰船安全的威胁,可以利用拖曳式角反射器假目标来干扰雷达,提高飞机的生存能力.拖曳式无源假目标的工作原理是利用角反射器雷达回波散射强的特性,将角反射器阵列组成的假目标放置于海面上,当受到敌方雷达威胁时,将假目标释放出去,利用假目标模拟实际的舰船目标.
对图26 所示的伯克级舰船模型进行一维距离像仿真,中心频率为3 GHz,雷达观察角度为θs=85°,φs=0°,仿真的一维距离像如图27 所示.在仿真时,探测雷达从舰船头部观察,海面总宽度为200 m,仿真的分辨率为0.5 m,图27 中蓝色为本文方法的仿真结果,灰色为FEKO 仿真结果.从海面舰船的一维像仿真可以看出,距离像的峰值对应着的是舰船主体上突起的两个二面角结构,尝试利用二十面体角反射器组成和舰船在该观察角度下相比拟的一维像的结构,设计的角反射器如图28 所示.同时也在相同的中心频率和雷达观察的分辨率的仿真条件下,模拟了二十面体角反组合的一维距离像,如图29 所示,并与图27 中舰船的一维像进行对比.目前,这组角反阵列只能模拟出舰船模型当前的一维距离像回波,从而干扰敌方测距雷达的接收信号形式,降低雷达的检测、识别和跟踪性能.还需要进一步地对角反阵列进行智能化的研究,探索出海上舰船目标电子对抗的新方法.
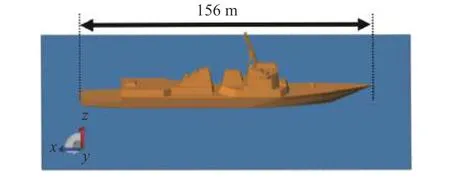
图26 伯克级舰船模型Fig.26 Burke-class ship model
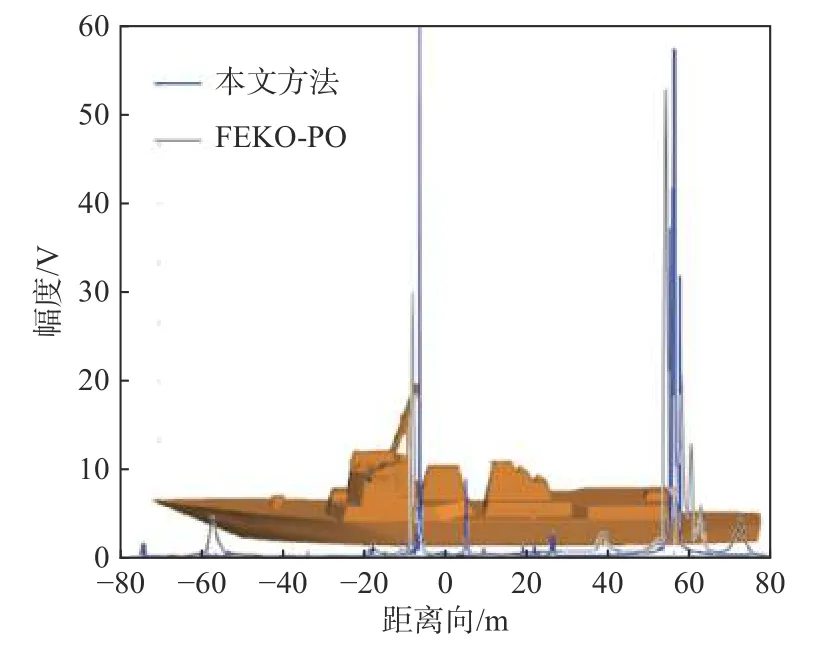
图27 伯克级舰船模型一维像Fig.27 One-dimensional image of Burke-class ship model

图28 角反射器阵列模型Fig.28 Corner reflector array model
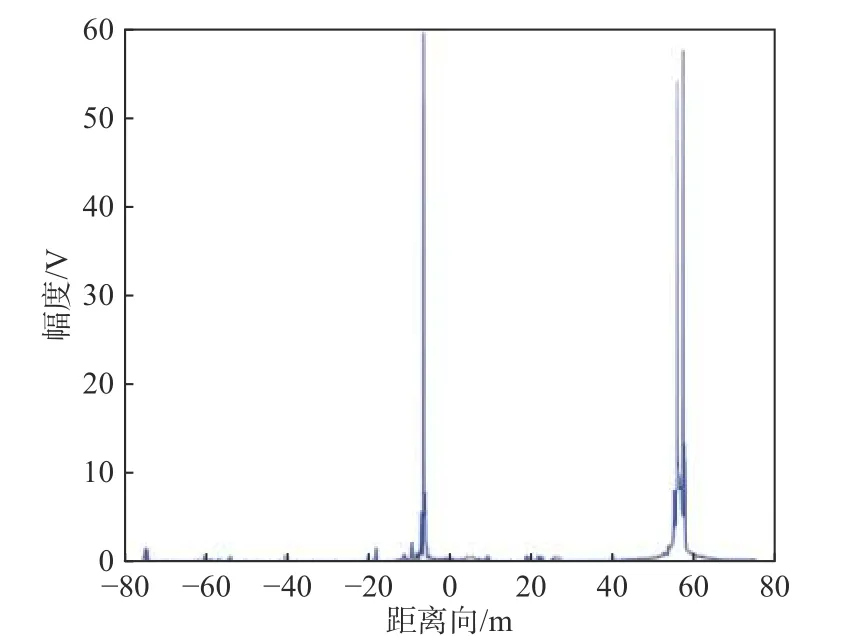
图29 角反射器阵列模型一维像Fig.29 One-dimensional image of corner reflector array model
4.8 海面舰船角反二维像仿真
对复杂的舰船与角反场景进行成像仿真,仿真场景分别如图30(a)和(b)所示,为港口+舰船+角反组合模型,港口上有集装箱、塔吊、油罐等模型,设置为金属目标,港口为水泥目标,设置介电常数为εr=(5.2+0.5j).海面的介电常数与图22 表述的仿真算例中的参数一致.合成孔径雷达(synthetic aperture radar,SAR)成像的雷达频率为10 GHz,带宽为5×107Hz.成像窗口为256×256,窗口范围为−150~150 m.成像角度为θs=70°,φs=67°.
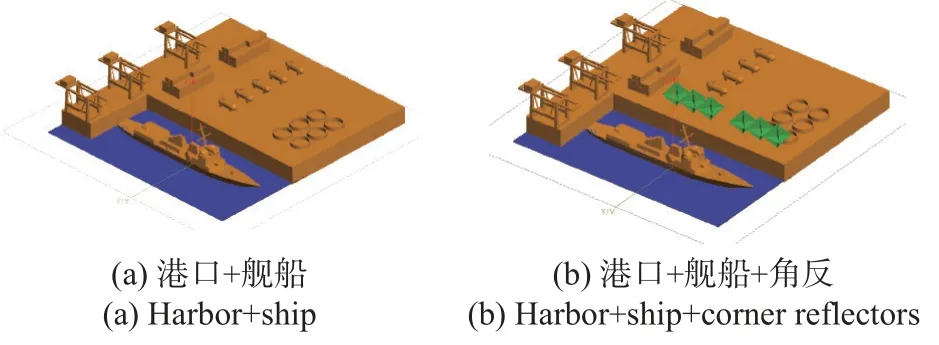
图30 港口复杂场景模型Fig.30 Complex harbor scene model
从图31 可以看出:在不含角反阵列场景中,舰船轮廓清晰,散射特征明显;加入角反阵列后,整个场景中的强散射点位于角反阵列处,原先的舰船模型的散射点强度相对变弱,可以认为角反阵列起到了改变目标在SAR 图像中散射中心分布特点的作用.

图31 港口复杂场景模型SAR 成像Fig.31 SAR imaging of complex harbor scene model
5 结 论
本文针对海面舰船与角反的电磁散射特性分析提出了耦合绕射修正的快速IPO 方法.利用FMM和GPU 加速的快速IPO 方法分析了海面舰船角反阵列组合,充分证明了算法在计算效率上的优势.同时,本文提出的绕射场修正方法一定程度改善了海面复杂的角反和舰船的散射场计算精度,补充了不同的散射机理,为舰船角反的海面特性的提取提供了有效的手段.

