H-ResGAN 在智能反射面辅助通信系统中的信道估计

张欣怡 江沸菠* 彭于波 董莉

（1.湖南师范大学信息科学与工程学院, 长沙 410000；2.湖南工商大学计算机学院, 长沙 410000）

0 引 言

随着5G 通信的普及，6G 通信技术也在探索中，以实现更快、更可靠的数据传输[1].为克服大规模MIMO 系统的高成本和高功耗问题，智能反射面（intelligent reflecting surface, IRS）技术作为一种可行的低成本和低复杂性的解决方案被提出[2].

每个IRS 均由大量的无源可重构反射单元构成，反射单元使用可编程的元材料制作，每个单元都可以独立对入射信号施加变化[3].由于IRS 的反射单元是无源的，与依赖有源传输设备的传统中继辅助通信系统相比，IRS 的功耗要低得多；且因为IRS 直接对入射信号进行反射，无热噪声[4].当信号发送方与接收方之间的视距通信受到阻碍时，IRS 可以通过软件编程智能配置无线传播环境辅助通信.制作IRS 反射单元的材料具有尺寸小、重量轻的特点，很容易涂覆在建筑物的外墙、天花板、墙壁等位置[2]，随时随地帮助信号进行传播.IRS 被认为是下一代无线通信系统的关键技术之一[5].

在通信过程中，为了尽可能准确地对接收到的数据进行译码，需要从接收信号的状态来对信道的特性进行估计，即信道估计.信道估计的目标是在最小化估计误差的同时尽量降低算法的复杂度.常用的信道估计方法是基于导频符号的估计[6-7]，在发送的数据流中插入已知的导频符号，然后用接收到的导频符号与原始的导频符号进行比较，得到导频位置的信道估计结果，利用这个结果可以完成非导频位置的信道估计.由于IRS 的无源特性，从IRS 辅助的通信系统中难以获取信道状态信息（channel state information, CSI），给信道估计带来了挑战[8].

文献[9]介绍了一个IRS 辅助的多用户MIMO通信系统，并提出了一种基于最小均方误差（minimum mean square error, MMSE）的信道估计协议.虽然这种方法具有良好的性能，但需要发送大量导频信号，降低了频谱效率，且在低信噪比(signal-to-noise ratio,SNR)场景下估计误差大.文献[10]提出了一种基于交替方向乘子法(alternating direction multiplier method,ADMM)的信道估计方法，将级联信道矩阵转换为稀疏矩阵恢复问题，降低了训练开销.但是基于压缩感知的信道估计方法需要使用具有高复杂度的非线性优化算法，才能达到较好的性能.近年来，深度学习（deep learning, DL）在通信领域得到了广泛的应用[11-12]，可以提取输入信号与输出信号之间的内在关系，实现更可靠的信道估计，且只须确定神经网络的输入和输出，从而避免了复杂的理论分析过程.文献[13]提出了两种基于残差神经网络的信道估计器，即单尺度增强深度残差（enhanced deep super-resolution,EDSR）网络和多尺度增强深度残差（multi-scale deep super-resolution, MDSR）网络，以获得准确的CSI，在系统复杂性和估计性能之间取得平衡.值得注意的是，虽然基于DL 的信道估计方法可以避免复杂的理论分析且节省导频开销，但由于神经网络中连续层的信息丢失，使用现有的基于DL 的方法难以生成更真实的信道矩阵[14].因此，在处理数据生成问题时，必须很好地设计和研究神经网络的损失函数，以减少学习过程中的信息损失.

生成对抗网络（generative adversarial networks,GAN）[15]通过两个网络的对抗训练，能够从有限的数据集中学习到数据的分布，从而生成满足特定分布的伪造数据.GAN 强大的学习能力在计算机视觉领域得到了广泛应用[16]，被应用到IRS 辅助的无线通信系统中.文献[17]利用IRS 信道的低秩结构，提出了基于GAN 的卷积盲去噪网络以获得准确的CSI.文献[18]提出了一个基于模型驱动的GAN 的信道建模框架，无需复杂的理论分析或数据处理，就能自主地学习IRS 与用户之间的信道分布.文献[19]设计了一个条件GAN 来估计IRS 辅助通信系统中的级联信道.但实际应用中，GAN 常常伴随着训练不稳定和梯度消失的问题.

本文提出了一种基于混合损失残差GAN（hybrid loss based residual GAN, H-ResGAN）的信道估计方法来解决IRS 辅助的毫米波无线通信系统中的信道估计问题.将条件最小二乘（least squares，LS）损失和L1 损失结合的混合损失作为H-ResGAN 的损失函数，使得神经网络能够快速稳定收敛，实现更好的信道估计性能.H-ResGAN 在不同SNR 和不同长度的导频序列下与其他信道估计方法进行了仿真实验的对比，结果表明，与传统的估计算法相比，HResGAN 对环境噪声更具鲁棒性，使用少量导频就能得到准确的信道估计结果.

1 系统模型

图1 所示为IRS 辅助的毫米波上行无线通信系统，当基站与用户间的视距（line-of-sight, LoS）路径被障碍物阻挡时，毫米波信号可经IRS 反射后传播至基站.在此通信系统中，用户持有的单天线设备、基站和IRS 都采用均匀方形阵列（uniform planar array, UPA）结构，其中基站的天线数量为M，IRS 由N个反射单元组成.

假设用户与IRS 之间的信道为ht∈CN×1，IRS 与基站之间的信道为Hr∈CM×N，用户和基站之间由于建筑物的阻挡无法进行LoS 通信.本文采用莱斯信道模型模拟通信信道，ht,LoS∈CN×1和ht,NLoS∈CN×1分别表示用户到IRS 的LoS 信道分量和非视距（non-line-ofsight, NLoS）信道分量，Hr,LoS∈CM×N和Hr,NLoS∈CM×N分别表示IRS 到基站的LoS 信道分量和NLoS 信道分量.ht,NLoS∈CN×1和Hr,NLoS∈CM×N的元素是独立同分布的随机变量，服从复高斯分布.ht,LoS∈CN×1和Hr,LoS∈CM×N可以分别表示为：

式中：dt为用户和IRS 之间的距离；dr为IRS 和基站之间的距离； λ为信号的波长；和分别为IRS 处的方位角和仰角；和分别为用户处的方位角和仰角；和分别为IRS 和用户对所考虑的方位角和仰角的阵列响应；和分别为基站处的方位角和仰角；和分别为IRS 处的方位角和仰角；和分别为基站和IRS 对所考虑的方位角和仰角的阵列响应.

根据莱斯信道模型，信道ht和Hr可分别表示为：

式中：ξNLoS和 ξLoS分别为从用户到IRS 的NLoS 路径损耗因子和LoS 路径损耗因子；ζNLoS和ζLoS分别为从IRS 到基站的NLoS 路径损耗因子和LoS 路径损耗因子； βt和 βr为莱斯因子.

对于图1 所示的通信系统，基站处的接收信号为

式中：Φ=diag(ejθ1,ejθ2,...,ejθN)为IRS 处的相位对角矩阵，θi∈[0,2π]为IRS 上第i个反射单元的相位；s为长度为 τ的导频序列；n=[n1,n2,...,nM]，nm∼CN(0,σ2)为基站第m根天线处的复高斯白噪声.( a)中e=[ejθ1,ejθ2,...,ejθN]T∈CN×1；( b)中定义H=Hrdiag(ht)，H∈CM×N称为级联信道.简单起见，假设θi=0, ∀i.

2 条件生成对抗网络(CGAN)

GAN 由生成器和判别器两个模型组成，生成器用于学习数据分布pdata(x)，生成与真实数据相似的伪造数据；判别器用于判断样本来自真实数据还是生成器伪造.生成器和判别器都可以是非线性映射函数，为了学习到真实数据的分布，生成器构建从随机噪声分布pz(z)到数据空间的映射G(z)，判别器D(x)输出单个标量表示样本来自真实数据而不是伪造数据的概率.原始的GAN 模型采用交叉熵函数作为损失函数，将判别网络当作分类器，如果判别器认为输入的是真实数据，则输出的结果为“1”，反之输出“0”.GAN的目标函数如下：

生成器的目标是用生成的伪造数据骗过判别器，使D(G(z))尽可能接近“1”，D(x)尽可能接近“0”，最小化目标函数VGAN(D,G).判别器的目标则是尽可能分辨出生成器伪造的数据和真实数据，使D(G(z))尽可能接近“0”，D(x)尽可能接近“1”，最大化VGAN(D,G).两个网络互相对抗训练，直到生成器学习到原始数据的分布，产生和原始数据高度相似的伪造数据，使判别器无法分辨出真实数据和生成器生成的伪造数据.

原始的GAN 是无条件模型，可以产生多样化的生成结果，但如果想生成某种特定类别的数据则缺乏相应的指导.如图2 所示，条件生成对抗网络（conditional generative adversarial networks, CGAN）[20]在原始的GAN 模型中加入一些额外信息y作为条件，使得GAN 的生成结果更加可控，y可以是任何类型的辅助信息.在手写数字生成实验中，如果不加入条件信息，则生成器生成的是0～9 的随机数字，如果将类别标签作为条件和噪声一起输入到生成器中，生成器生成的则是和类别标签一致的数字.CGAN 的目标函数如下：

3 信道估计方案

3.1 信道图像生成

本文中，接收到的导频信号Y和级联信道矩阵H可以看作尺寸分别为M×τ×2和M×N×2的双通道图像，复数矩阵的实部和虚部分别对应图像的两个通道.通过这样的变换，信道估计问题就转换成为信道图像生成问题[21]，可以使用GAN 来进行信道图像生成.由于接收到的信号Y中包含导频信息和噪声，其中导频信息可以被视为条件信息对输出结果进行限制，因此，可将Y用作条件输入.

如图3 所示，H-ResGAN 的信道估计过程可以分为离线训练和在线估计两个阶段.离线训练阶段，利用基站接收到的信号Y对GAN 进行训练，通过对这些数据进行学习，构建出信道数据和接收信号之间的非线性关系.生成器根据接收到的信号Y估计信道矩阵，生成信道图像，判别器负责区分输入的是真实的信道图像还是生成器生成的假信道图像.训练完成后进入在线估计阶段，将相同信道条件下接收到的信号输入到训练好的生成器中，可以迅速得到对应的信道数据.

图3 H-ResGAN 信道估计过程示意图Fig.3 Diagram of the H-ResGAN channel estimation process

3.2 残差生成对抗网络

常规的网络结构随着网络层数增加容易导致梯度消失，网络难以收敛，从而需要花费较长的训练时间，并且生成的信道图片不够清晰.残差网络[22]使用多个残差块来构建深度网络，每个残差块通过跳跃连接的方式将块的输入和输出相加，在不增加额外参数的同时，可以加强信息的跨层流动，提高模型的训练效果.因此，本文使用残差块来构建信道生成网络，可以在提高信道图片清晰度的同时加快网络的收敛速度.

本文提出一个用于IRS 辅助无线通信系统信道估计的残差生成对抗网络，包括一个信道生成网络和一个信道判别网络.如图4 所示，信道生成网络以残差块为核心，每个残差块包括两个卷积层（convolution layer, Conv）和两个批归一化（batch normalization,BN）层，线性整流单元（rectified linear unit, ReLU）作为激活函数，使用跳跃连接将网络连接起来.首先使用一个卷积层和一个ReLU 层提取接收信号的低层特征，然后使用上采样模块（Upsampling）将接收信号图片放大至信道图片的尺寸，再用4 个相同结构的残差块进行高层特征提取，最后使用一个卷积层重建信道图像.使用残差信道生成网络能有效改善由于神经网络层数加深导致的梯度消失和训练不稳定的问题，帮助我们得到清晰的信道图片.

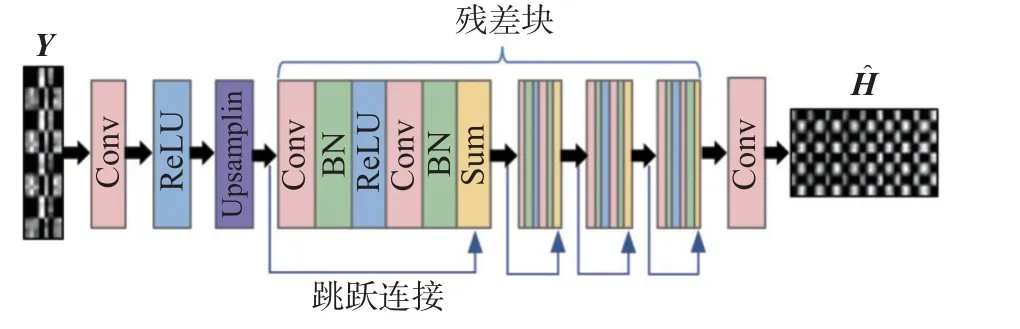
图4 生成器结构Fig.4 Generator structure

如图5 所示，信道判别网络是一个多层感知机（multi-layer perceptron, MLP），用于评估生成器生成的信道图片质量.首先使用一个Flatten 层将二维矩阵转化为一维向量，中间层为3 个全连接层（Dense），BN 层通过将每个单元的输入归一化来稳定学习，同时帮助梯度传播，使用LeakyReLU 作为激活函数，最后通过一个全连接层和Sigmoid 激活函数输出一个标量，表示输入的信道图片是真实信道而不是生成器生成的假信道图片的概率.

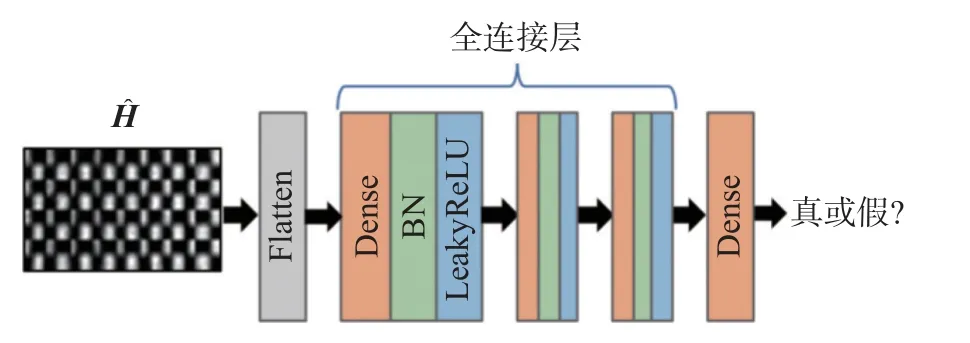
图5 判别器结构Fig.5 Discriminator structure

3.3 损失函数

3.3.1 条件LS 损失

原始的GAN 使用交叉熵损失函数，将判别器作为分类器，在训练过程中经常出现网络难以收敛的情况，无法生成合理的信道图片.为了解决这个问题，参考最小二乘GAN(least squares GAN, LSGAN)[23]，使用LS 损失函数代替交叉熵损失函数.最小化LSGAN 的目标函数可以使皮尔森卡方散度最小化，因此，使用LS 损失能够生成比交叉熵损失更高质量的信道图像，并且在学习过程中表现更稳定.LSGAN的损失函数如下：

CGAN 通过在输入中加入条件信息，可以对生成器产生的结果进行控制，避免生成结果过于自由.因此，为了对生成结果加以约束，使得生成的信道更接近真实信道，本文对LSGAN 的损失函数进行改进，将其扩展为条件模型，从而可以将接收到的信号作为条件输入，来对信道估计结果进行限制，产生更符合实际传输情况的信道图片.改进后的条件LS 损失为：

3.3.2 混合损失

为使生成器生成的信道图片在像素点上更接近真实信道图片，在信道生成器的损失函数中加入L1 损失[24]，表达式为

最终，H-ResGAN 的目标函数为

3.3.3 收敛性证明

将信道生成器固定，令信道判别器的目标函数导数为0，可以求出最优的判别器为

式中，pg(x)为G(z|y)生成的样本分布.

向VLS(G)中人为添加一个与G无关的常数项得到C(G)，因为常数项中不包含G的参数，加上后不会改变VLS(G)的最优值.将D∗(x)代入VLS(G)，得到：

4 仿真结果与分析

为了评估所提方案的性能，使用归一化均方误差（normalized mean square error, NMSE）来衡量估计的信道Hˆ与目标信道H之间的差距，NMSE 越小，算法的信道估计性能越好.NMSE 表达式为

式中，‖·‖F表示矩阵的F 范数.通过计算10lg{·}将NMSE 转化为以分贝为单位的形式.

仿真场景是在28 GHz 的毫米波频段内进行载波频率fc=24.2 GHz 的通信.图6 所示的三维坐标中，基站、IRS 和用户的坐标分别为(20, −20, 10) m，(−20, 20, 2) m 和(a,b, 1） mm，假设用户(a,b, 1) m 在圆心为（10, 10） m、半径为10 m 的圆内移动，所持设备高度为1 m.

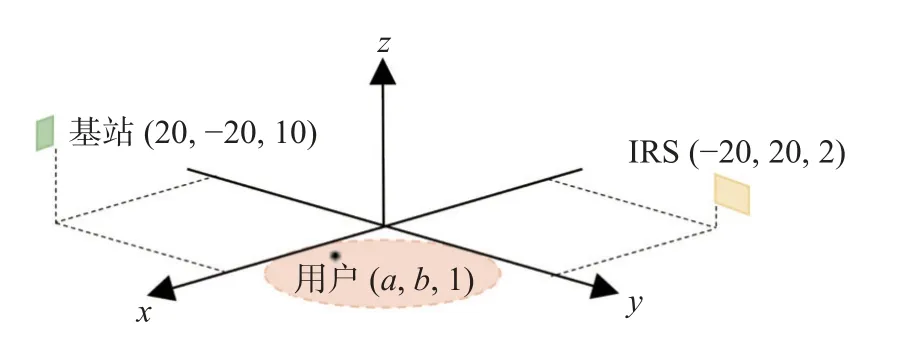
图6 基站、IRS 和用户的坐标图(单位:m)Fig.6 BS, IRS and user coordinates

使用莱斯衰落信道模型，采用3GPP TR 38.901的城市微蜂窝街道场景下的路径损耗模型模拟路径损耗，仿真参数如表1 所示.

表1 仿真参数Tab.1 Simulation parameters

在上述前提条件下，使用NMSE 来衡量算法的性能，SNR=15 dB，导频序列长度从8 增加至72，比较不同导频序列长度下H-ResGAN 和基于导频的LS 算法[6]、 基于压缩感知的正交匹配追踪(orthogonal matching pursuit, OMP)算法[25]和近似消息传递（approximate message passing, AMP）算法[26]等几种传统信道估计算法的性能表现，结果如图7 所示.可以看出，当导频长度增加时，各算法的NMSE 值都呈下降趋势.在导频序列长度为8 时，LS 算法、OMP 算法和AMP 算法的NMSE 值略小于0 dB，而H-ResGAN算法的NMSE 值为−14 dB，且随着导频序列长度增加，NMSE 值下降不明显，说明HResGAN 算法的性能受导频序列长度影响不大，在导频数量较少时也能表现出比其他算法更优的性能.H-ResGAN 算法能够大大减少导频符号的使用，在保证信道估计结果准确性的同时，提高通信效率.

图7 不同导频数量下4 种算法的NMSEFig.7 NMSE performance of 4 methods for different number of pilots

除上述3 种传统信道估计算法外，还将HResGAN 算法与基于GAN 的卷积盲去噪网络(GANbased convolutional blind denoising network, GANCBD)[17]进行了对比.H-ResGAN 使用长度为8 的导频序列进行信道估计，而其他算法的导频序列长度为65.SNR 从−10 dB 到20 dB 时，5 种不同方法信道估计得到的NMSE 值如图8 所示.可以看到，随着SNR 的增加各算法的NMSE 均逐渐减小.其中，LS 算法在SNR 低时性能最差，其在进行信道估计时忽略了噪声的影响，在信道噪声较大时信道估计的准确性低.SNR 小于0 dB 时，OMP 算法和AMP 算法表现接近；SNR 大于0 dB 时，OMP 算法的NMSE 曲线趋于水平，AMP 算法的表现更优.SNR 小于10 dB时，GAN-CBD 算法比传统方法性能表现差；但SNR大于15 dB 时NMSE 最小，具有最佳性能.随SNR 增大H-ResGAN 算法的NMSE 曲线变化较小，当SNR 小于15 dB 时，H-ResGAN 算法的估计误差小于其他信道估计方法，说明H-ResGAN 的信道估计方法受SNR 影响较小，对环境噪声更具鲁棒性，在低SNR 环境下具有更好的性能.

图8 不同SNR 下5 种算法的NMSEFig.8 NMSE performance of 5 methods for different SNRs

SNR=15 dB，将反射单元数量从64 增加至320，H-ResGAN 使用的导频序列长度为8，其他方法的导频序列长度为50，5 种算法的NMSE 仿真结果如图9所示.可以看到，随着反射单元的数量增加，各算法的NMSE 值均增大.反射单元数量增加意味着信道矩阵的维度变大，需要更多的导频序列来进行信道估计，不增加导频数量信道估计的性能就会变差.从图9 中可以看出，GAN-CBD 算法和H-ResGAN 算法表现均优于传统信道估计算法，但是当反射单元数量增大时，GAN-CBD 算法的性能下降更为明显，HResGAN 算法的NMSE 曲线变化相对较小，保持较低的NMSE 值，说明H-ResGAN 的信道估计方法受反射单元数量影响较小，使用少量导频也能实现较好的性能.

图9 不同反射单元数量下5 种算法的NMSEFig.9 NMSE performance of 5 methods for different number of reflective elements

为证明所提网络结构的有效性，对比不同神经网络结构对信道估计结果的影响，结果如图10 所示.GAN 的生成器分别使用U-Net 结构[27]和MLP 结构，判别器均使用MLP 结构，与H-ResGAN 进行对比实验，同时与经典的深度卷积GAN（deep convolution GAN, DcGAN）进行对比.SNR=15 dB，导频序列长度为8，损失函数均使用LS 损失和L1 损失相结合的混合损失函数，将接收到的信号Y作为输入.从图10 中可以看出，随着训练过程中迭代次数的增加，测试数据的NMSE 值均逐渐减小.其中，H-ResGAN 经过第1 轮迭代得到的NMSE 值就已优于MLP 结构的GAN 和DcGAN 在30 轮迭代之后的结果，第10 轮迭代H-ResGAN 已收敛至较好的结果，而使用UNet 结构的GAN 在30 轮迭代之后才具有相近的性能表现.最后，针对相同的H-ResGAN 结构，分别使用本文提出的LS 与L1 相结合的混合损失和经典的GAN 损失与L1 损失结合的损失函数进行对比实验，实验结果表明，使用两种不同损失函数的HResGAN 随着迭代次数增加具有相似的变化趋势，均优于其他网络结构，其中，本文提出的LS 与L1 相结合的混合损失H-ResGAN 的训练曲线更为平滑，训练过程更稳定.

图10 不同网络结构随迭代次数变化的NMSEFig.10 NMSE of different network structures with the number of iterations

在相同的实验条件下，分别将批量大小设为8、16、32、64，对H-ResGAN 进行训练，实验结果如图11所示.可以看出：批量越小，神经网络收敛所需的迭代次数越少；批量越大，神经网络收敛所需的迭代次数越多.

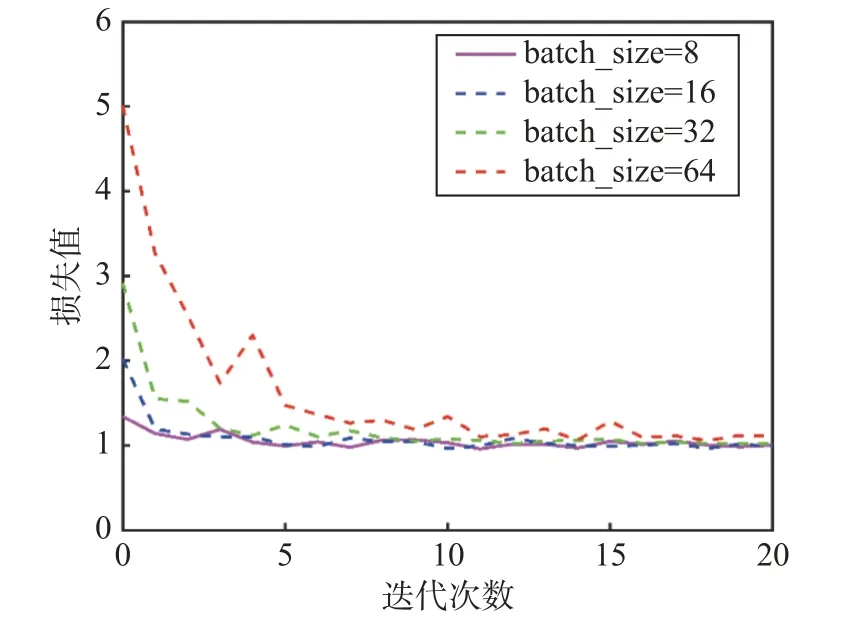
图11 不同批量大小随迭代次数变化的损失曲线Fig.11 Loss curves for different batch sizes with number of iterations

5 结 论

在基站与用户间的LoS 路径被障碍物阻挡时，本文利用IRS 辅助毫米波无线通信帮助毫米波信号从用户处传播至基站.在此系统环境中，由于IRS 具有大量元件，信道维度高，传统的非基于DL 的方法需要发送大量导频信号或者具有较高的算法复杂度，而常规的神经网络信道估计方法需要大量带标签的数据进行训练，且性能难以提升.因此本文提出H-ResGAN，将IRS 辅助的通信系统中的信道估计问题转换为信道图像生成问题.该网络的生成器以残差块为核心，可以缓解神经网络过深导致的梯度消失问题，增强训练过程的稳定性，同时采用条件LS损失与L1 损失相结合的混合损失作为损失函数，帮助神经网络更稳定地训练，提高信道估计的准确性.仿真结果表明，H-ResGAN 对环境噪声更具鲁棒性，且估计误差达到−14 dB，显著低于传统方法的估计误差.另外，与传统的估计算法相比，H-ResGAN 使用少量导频就能实现准确的信道估计结果，可以显著提升通信效率.

未来工作将进一步致力于：1）对信道判别网络进行改进，进一步提升网络性能；2）使用基于光线追踪数据构建的数据集进行实验，进一步研究如何在真实场景下实现准确的信道估计；3）增加与最新的信道估计算法的对比实验，如ADMM 算法[13]和EDSR 算法[18]等.