基于对消超表面的角反射器宽带RCS 减缩设计
陈强 陈燕娜 袁方 白佳俊 郑月军 付云起
(1.国防科技大学电子科学学院, 长沙 410073;2.国防科技大学第63 研究所, 南京 210000;3.军事科学院, 北京 100080)
0 引 言
由两个或多个互相垂直的金属面组成的角反射器结构具有较强的雷达波反射能力,但其雷达散射截面(radar cross section,RCS)较大[1-2].在真实装备目标上,为降低被发现概率,提高生存能力,一般要避免采用角结构[3].但是很多装备平台上广泛存在的角结构不可避免,包括飞机尾翼、舰船的舰岛、坦克的炮塔等,这些角结构成为平台的主要雷达散射源.因此,研究角结构的RCS 减缩方法对提升装备平台生存能力具有重要作用.
二面角反射器(dihedral corner reflector, DCR)是最基本的角反射器结构,其RCS 减缩设计对角反射器结构的RCS 控制具有重要意义.范菊红等分析了DCR 的夹角和尺寸变化时的RCS 特性变化规律[4].张然等分析了在不同夹角的 DCR 中加载Salisbury 屏后单一频点处的RCS 减缩性能和极化散射特性[5].祝寄徐等提出在二面角和三面角反射器中加载超材料吸波体来减小角反射器RCS[6-7],但由于超材料吸波体单元的吸波性能和带宽有限,仅实现了最大3.6 dB 的RCS 减缩.陈海燕等提出采用条带式相位对消方法减缩二面角RCS[8],仅在5 GHz 周围较窄频带实现了一定的RCS 减缩性能.研究者针对角反射器结构的RCS 减缩进行了初步探索,但是RCS 减缩性能和覆盖带宽均有限.
超表面是人工设计的亚波长单元结构,能够调控雷达波幅度和相位,在雷达隐身应用中得到了深入的研究.在幅度调控方面,通过在超表面单元加载电阻或有耗结构能够实现对入射电磁波的吸收[9-11],减小反射回波能量,实现RCS 减缩.在相位调控方面,对金属表面不同区域的相位进行调控,能够实现对散射波的宽带相位对消设计[12-15],比如超表面子阵交叉排布的棋盘结构能将金属表面镜像反射方向的波束分散到其他方向而产生反射零点,实现对镜像方向双站RCS 的减缩.
雷达隐身技术更关注对目标单站RCS 的减缩控制,为减缩二面角在宽频带的单站RCS,本文设计了两种超表面单元,在X 和Ku 波段产生180°±37°的相位差[15],两种超表面子阵组成棋盘结构,实现了宽带相位对消.并将宽带相位对消超表面棋盘结构加载在二面角内侧表面上,通过宽带的相位对消实现对二面角单站RCS 的宽带减缩设计.
1 相位对消减缩二面角RCS 原理
1.1 相位对消原理
当平面波垂直入射到如图1 所示的两个相邻的理想电导体(perfect electronic conductor,PEC)和理想磁导体(perfect magnetic conductor,PMC)表面时,由于两者反射波的相位相差180°,因此散射波会在空间中产生干涉相消效果.

图1 2×2 棋盘结构示意图Fig.1 2×2 checkboard structure
棋盘结构的相位对消原理可以通过阵列理论来分析[16],其散射过程可等效为2×2 天线阵列的辐射过程.当平面波垂直入射到每格边长为l的棋盘结构表面时,在表面产生幅度相等、相位相反的表面电流,可等效为功率相同、相位相反的四个基本辐射天线.
PEC 单元和PMC 单元等效的基本天线单元的的辐射场可以表示如下:
式中:ϕ1=180°,ϕ2=0°分别为PEC 和PMC 单元的反射相位.因此2×2 棋盘结构的散射场为
F1和F2是阵列因子,表达式分别为:
式中:l为棋盘结构子阵大小;φ和θ 分别为球坐标系下的方位角和俯仰角.用Matlab 仿真了这种棋盘结构的散射方向图,结果如图2 所示.可以看出,在平面波沿−z垂直入射下,当l=λ 时,散射波束出现在φ=45°/135°、θ=±45°四个方向,而在反射的+z方向由于相位相反,对消后散射幅度取得最小值.因此,棋盘结构实现了垂直方向的单站RCS 减缩.
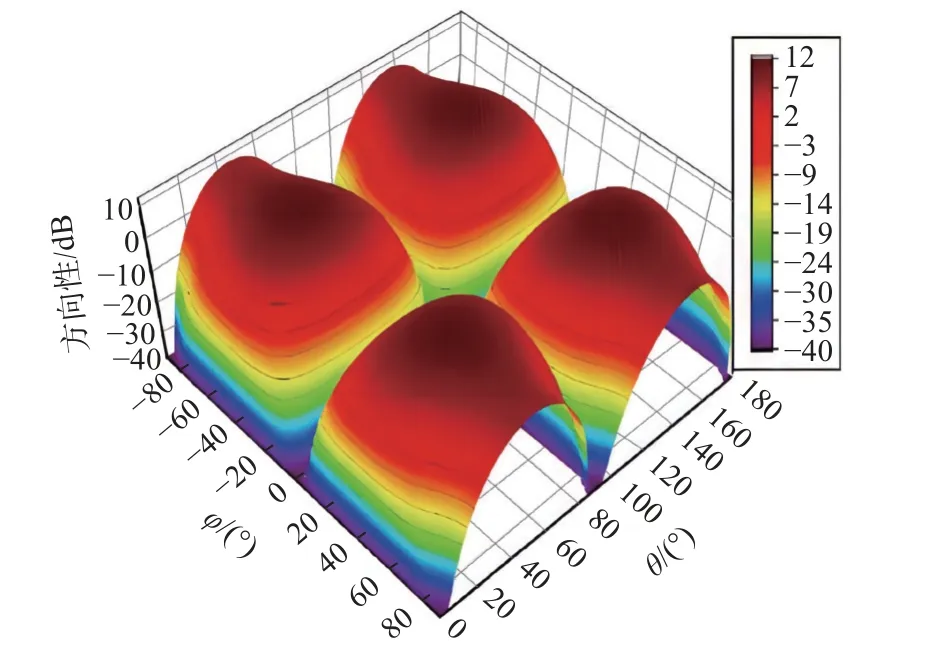
图2 l =λ 时2×2 棋盘结构散射方向图Fig.2 Scattering pattern of 2×2 checkboard structure with l =λ
而当平面波斜入射到棋盘结构表面时,假设各子阵的反射相位差仍保持180°,将在与入射方向镜像的方向上满足相位对消条件,会减小平面在镜像方向的双站RCS[8].
1.2 二面角RCS 减缩原理
相互垂直的两个金属面构成的装置称为DCR.二面角是角反射器的基本结构,RCS 增强是其基本特性,其反射机理如图3(a)所示.当平面波入射到其中一个金属面时,其镜面反射入射到另一个金属面,再次经镜面反射后反射出去,根据几何光学原理,反射波的方向与入射波方向一致,因此呈现较大的后向RCS.为减小二面角的后向RCS,可将相位对消棋盘结构加载于其中一个金属面内侧.同样可以利用电磁波的几何光学特性来分析其RCS 减缩原理,如图3(b)所示.平面波照射到棋盘结构表面时,反射波束变成四个对称的分波束,并在与入射方向镜像的方向上产生散射零点.经过另一个金属表面的镜面反射后,棋盘结构形成的零点沿入射波方向反射回去,而四个分裂波束被偏折到其他方向.当入射波首先照射到金属表面再反射到棋盘结构表面时,根据光路可逆原理,将得到相同的零点散射状态.因此,将相位对消棋盘结构加载在二面角结构的其中一个面上,可以实现对二面角的单站RCS 减缩设计.
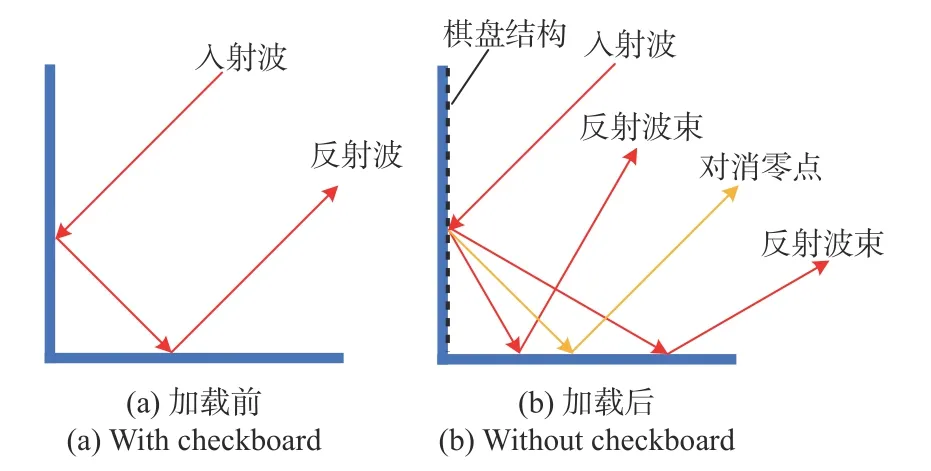
图3 加载棋盘结构前后的DCR 反射波路径Fig.3 Refelection patch of PEC DCR with and without checkboard structure
2 超表面棋盘结构设计
2.1 超表面单元设计
棋盘结构实现相位对消的关键在于两种结构的反射相位差达到180°,不同位置的反射波在空间中实现干涉相消.PEC 和PMC 都是材料的理想状态,其反射相位分别为180°和0°,但是现实中不存在PMC 材料.为满足棋盘结构的相位对消条件,实际设计中通常选择两个反射相位差达到180°的超表面单元来代替PEC 和PMC.本文设计了十字嵌套环结构和变型Jerusalem 十字结构作为超表面单元的上层结构,超表面-1 和超表面-2 的周期性结构的图形如图4所示.超表面单元的介质基板为F4B,相对介电常数为2.65,厚度为3 mm.具体参数尺寸列在表1 中.

表1 结构参数Tab.1 The structural parametersmm
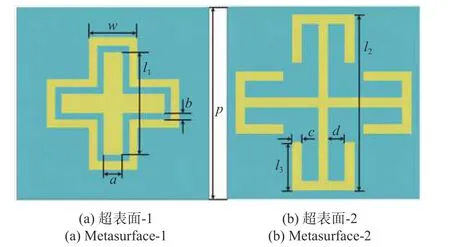
图4 超表面单元Fig.4 Metasurface unit cell
超表面-1 和超表面-2 的反射系数相位差如图5所示.根据W.Chen 等人提出的RCS 减缩经验公式,要实现10 dB 以上的相位对消RCS 减缩,两个超表面单元间的反射相位差需要在180°±37°范围内[15].两个超表面单元满足此条件的带宽为7.6~17.6 GHz.
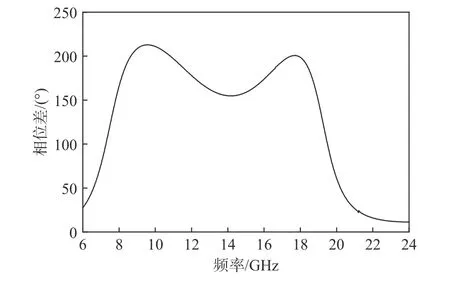
图5 垂直入射下两个超表面单元的相位差Fig.5 Phase difference between the two metasurface unit cells under normal incidence
2.2 超表面棋盘结构
将两个超表面单元的子阵交叉排布组合成棋盘结构,超表面单元组成的子阵大小会影响散射波束的空间合成分布.考虑子阵分别包含4×4,6×6 和12×12 个超表面单元等情况,子阵如图6 所示.每个棋盘结构均包含24×24 个超表面单元,尺寸均为144 mm×144 mm.对三种超表面棋盘结构在平面波垂直入射下的散射特性进行全波仿真,分析对应的垂直方向上棋盘结构的单站RCS,并与同尺寸的金属平板进行对比,结果如图7 所示.可以看出,不同子阵大小对低波段的相位对消影响较大,在8~12 GHz 波段内,子阵越小RCS 减缩效果越弱.原因在于两个超表面单元在该波段的相位偏差较大,而且较小的子阵尺寸电长度小于半波长,影响棋盘结构的相位对消结果.12×12 子阵大小的棋盘结构相较于同尺寸的金属板,8.8~10.6 GHz 内RCS 减缩8 dB,7.7~18.0 GHz 范围内RCS 缩减10 dB 以上,覆盖了X 波段和Ku 波段,与180°±37°相位差的带宽基本吻合.
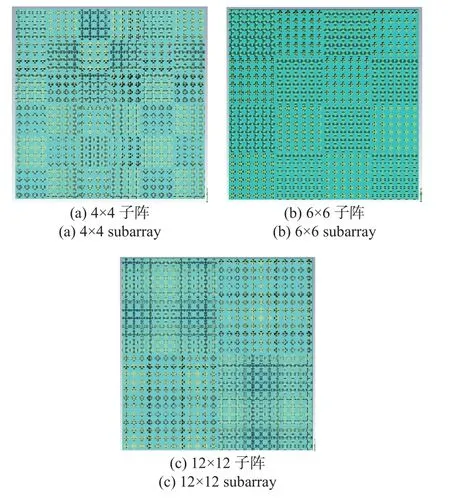
图6 三种超表面棋盘结构排布方式Fig.6 Three subarray arrangements of the checkboard structure
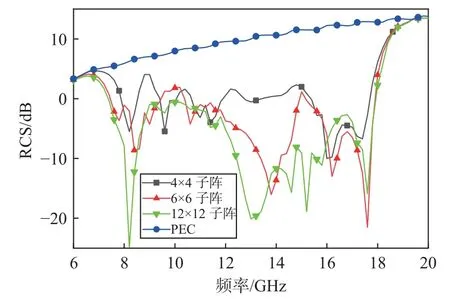
图7 垂直入射条件下不同子阵排布棋盘结构的单站RCSFig.7 Monostatic RCS of the checkboard structure with different subarray arrangement under normal incidence
图8 所示为三个频点(9.2 GHz,12 GHz,16.6 GHz)处棋盘结构的双站散射.相较于理想金属板,棋盘结构在垂直方向的回波能量明显降低,能量主要集中在周围的四个方向上,中心单站散射点为周围幅度极小值.相比理想金属平面的反射,超表面棋盘结构将散射波主波束对消为幅度减弱、相互对称的四个小波束.
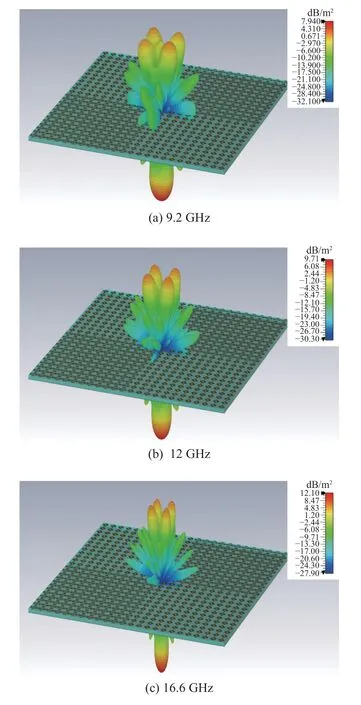
图8 垂直入射时三个频点处棋盘结构的双站散射Fig.8 Bistatic RCS of the checkboard structure at three frequencies under normal incidence
综上所述,仿真结果验证了超表面棋盘结构具有明显的宽带相位对消和RCS 缩减特性.然后将超表面棋盘结构加载于二面角结构中分析对二面角的单站RCS 减缩效果.此外,由于超表面单元具有对称结构,是极化不敏感的,因此以上分析仅给出了一种极化模式的结果,另一极化下具有类似的RCS 减缩效果.
3 二面角RCS 减缩设计
3.1 斜入射条件下的棋盘结构
超表面棋盘结构加载在二面角时,大部分情况下接收到的是斜入射的电磁波.图9 所示为两个超表面单元在斜入射条件下的反射相位差.可以看出:随着入射角增加,两个单元的相位差增加,部分波段超出180°±37°相位差的对消条件;入射角度为45°时在10 GHz 频带附近相位差超出180°±37°的相位差范围,理论上会影响该波段附近相位对消效果.
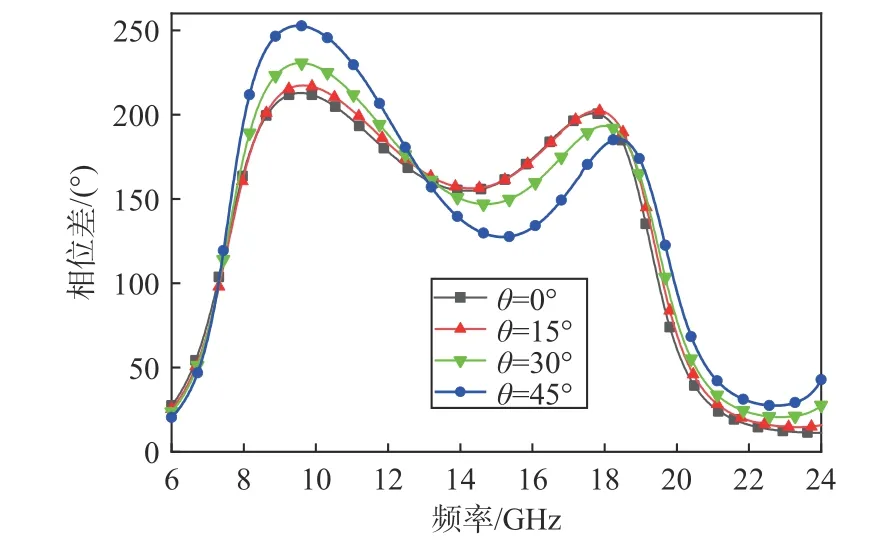
图9 不同入射角下两个超表面单元的相位差Fig.9 Phase difference between the two metasurfaces under different incidence angles
对12×12 子阵的棋盘结构在45°斜入射条件下的双站散射进行全波仿真,图10 所示为三个频点(9.2 GHz,12 GHz,16.6 GHz)处的三维双站散射图.可以看出在9.2 GHz 和16.6 GHz 处,该棋盘结构都产生了明显的相位对消效果,散射波束分裂成四个能量较小的波束,在镜像方向上产生了反射零点;而在12 GHz 处相位对消效果较弱,在镜像方向仍有较明显的散射波束.
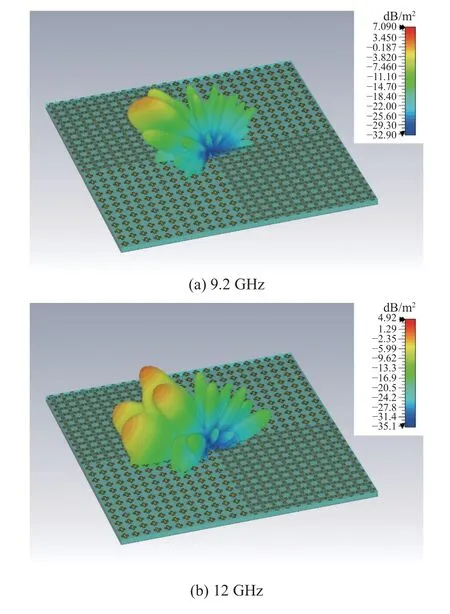
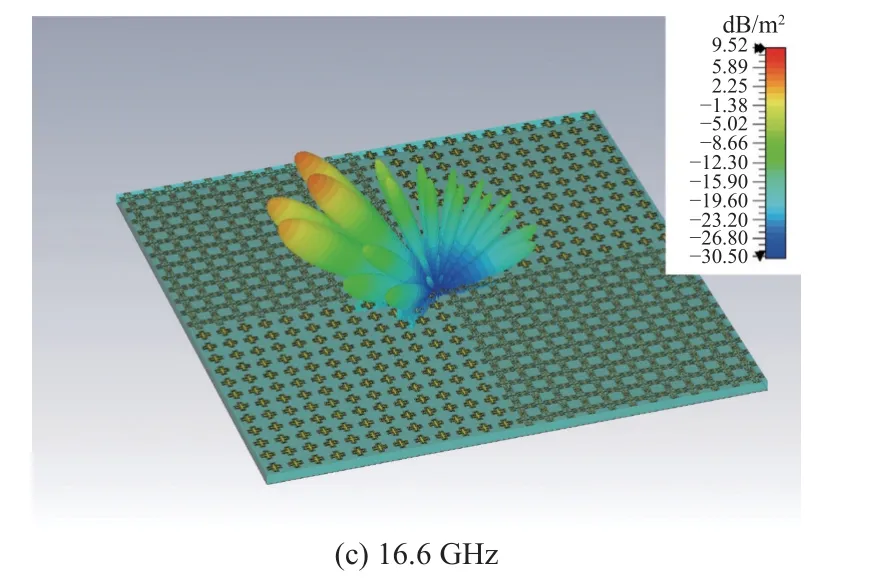
图10 45°斜入射时12×12 子阵棋盘结构的双站散射Fig.10 Bistatic RCS of the checkboard structure with 12×12 subarray under 45° incidence
3.2 加载棋盘结构减缩二面角RCS
将不同子阵大小的超表面棋盘结构加载到二面角中的一个面,对二面角的双站散射进行全波仿真分析.二面角的两个面尺寸相同,为144 mm 边长的正方形.平面波入射方向沿二面角的中分线方向,与每个面的夹角均为45°.同时以同尺寸的纯金属二面角结构作为对照来评估棋盘结构对二面角的RCS 减缩性能.图11 所示为加载棋盘结构的二面角仿真设置.加载不同子阵大小棋盘结构的二面角和金属二面角的单站RCS 结果如图12 所示.可以看出加载棋盘结构后二面角在X 和Ku 波段内的单站RCS 得到明显降低.12×12 子阵的棋盘结构对二面角的RCS 减缩效果较好,特别在9.2 GHz 和16.6 GHz 处将单站RCS 减缩了20 dB 和29.5 dB;而在12 GHz处由于斜入射对消效果不好,单站RCS 减缩仅有6 dB 左右.
根据图12 所示结果,选定子阵大小为12×12 个超表面单元对二面角的一个面进行加载.采用仿真软件CST 分析不同入射角度下加载对消超表面对二面角结构的单站RCS 减缩性能,结果如图13 所示.入射角为平面波入射方向与二面角不加载超表面的金属面的夹角,入射角为45°时平面波正好沿二面角的中分线方向入射.结果表明:入射角15°时,单站RCS 减缩效果更好,在整个8~18 GHz 频带内均减缩了10 dB 以上,特别在12~18 GHz 的Ku 频段内减缩了15 dB 以上;随着入射角增加,单站RCS 减缩量逐渐减少,主要是因为随着入射角增大,两种超表面单元的相位差逐渐增大,对消效果减弱.
为分析不同波段棋盘结构对二面角单站RCS 减缩效果的差异原因,给出图14 所示在三个频点(9.2 GHz,12 GHz,16.6 GHz)处加载12×12 子阵棋盘结构的二面角的三维双站散射结果.可以看出:在9.2 GHz 和16.6 GHz,在入射方向产生了明显的对消零点,主要散射能量被分到了相邻其他角度的四个波束上,极大减小了二面角的单站RCS.在12 GHz 处,由于图10 所示该频点处相位对消效果较弱,导致回波方向上仍然有较强的回波能量,因此单站RCS 减缩较弱.
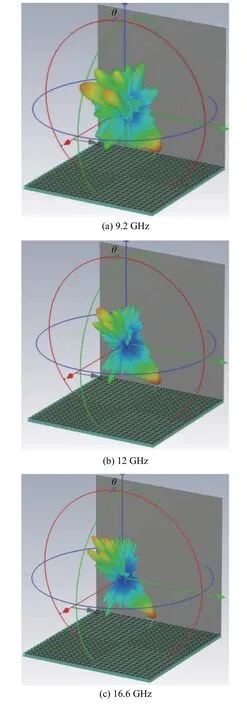
图14 加载棋盘结构的二面角的双站散射Fig.14 Bistatic RCS of DCR with checkboard structure
图15 所示为加工的12×12 子阵棋盘结构样件及贴附于二面角侧面的二面角样件.在微波暗室用两个靠近的喇叭天线测量不加棋盘结构的DCR 反射回波,然后测量加载棋盘结构的DCR 的回波,二者作差即为由棋盘结构引起的DCR 的单站RCS 减缩结果,测试结果与45°入射下的仿真结果对比如图16所示.结果表明通过加载棋盘结构的相位对消超表面,在X 和Ku 波段实现了对DCR 的宽带RCS 减缩.但是由于加工误差、测试过程中两次样件摆放角度误差以及入射角度误差等因素,测试结果与仿真结果有一定偏差.

图15 棋盘结构及加载棋盘结构的DCR 样件Fig.15 Prototype of the checkboard structure and the DCR with checkboard structure
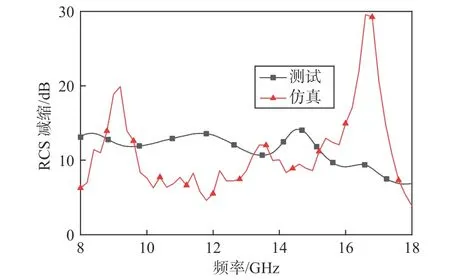
图16 DCR 加载棋盘结构后的单站RCS 减缩结果Fig.16 Measured RCS reduction of the DCR after loaded with checkboard structure
4 结 论
论文提出了基于相位对消超表面的角反射器结构的RCS 减缩方法.设计了7.6~17.6 GHz 频带内实现180°±37°相位对消的两种超表面单元,组成了12×12 子阵的棋盘结构来产生宽带相位对消并减缩平面的镜像双站RCS.将棋盘结构加载在二面角侧面实现了覆盖X 和Ku 波段的二面角单站RCS 减缩,最大RCS 减缩达到29.5 dB.这种相位对消棋盘结构未来须进一步研究棋盘结构对非直角反射结构的RCS 减缩设计,可用于不改变原结构外形尺寸条件下对现有装备的角结构进行低成本、隐身化改造.
——2022 F1意大利大奖赛

