车轮多边形磨耗对车桥耦合振动响应的影响

唐德发，吴梦雪，徐昕宇，张钞奕，李永乐

(1.西南石油大学土木工程与测绘学院,成都 610500; 2.中铁二院工程集团有限责任公司,成都 610031; 3.西南交通大学土木工程学院,成都 610031)

引言

车轮多边形磨耗也叫做车轮谐波磨耗,是车轮踏面在圆周方向出现的波形磨耗,广泛存在于铁路运输现场[1-4],但目前对其形成机理尚缺乏统一认识。车轮多边形磨耗会使系统产生高频振动以及更大的轮轨冲击力。这种高频振动可能造成车辆和轨道零部件的损坏,还会通过轨道传递至桥梁结构,对桥梁结构的疲劳性能造成影响。而轮轨冲击力的增大以及车轮多边形磨耗引起的滚动噪声将会严重降低列车行驶安全性和旅客乘坐舒适性。因此,车轮多边形磨耗研究一直受到学者们的广泛关注。

在车轮多边形磨耗成因方面,赵晓男等[5-6]研究发现,轮轨间蠕滑力饱和引起的摩擦自激振动、列车制动滑动易引发车轮多边形磨耗;金学松等[7-8]详细研究了高速列车车轮多边形磨耗的形成机理、影响和控制措施;康熙等[9]根据现场测试和多体动力学仿真结果研究了高速列车车轮偏心磨耗的形成机理与发展规律。在车轮多边形磨耗对列车动力响应的影响方面,罗仁等[10]考虑轮对的弯曲变形,研究了车轮多边形磨耗对车辆系统动力学性能的影响,发现车轮多边形磨耗使轮轨垂向力显著增大,但对列车运行的平稳性影响不大;张洁娟等[11]通过分析车轮多边形磨耗对某高速动车组动力学性能的影响规律发现,车轮多边形磨耗对列车垂向振动响应的影响更为显著;吴磊等[12]通过建立直线电机列车-轨道耦合动力学模型,分析了不同磨耗程度车轮对轮轨法向力和脱轨系数的影响;王忆佳等[13]采用车轮圆周轮廓法建立了车轮多边形磨耗模型,计算了高速运营状态下周期性车轮多边形磨耗对车辆动力学性能的影响,以轮轨垂向力为指标划定了车轮多边形磨耗的安全区域;WU等[14-15]和胡晓依等[16-17]的研究表明,与刚性轮轨相比,柔性轮轨加速了车轮多边形磨耗的发展,使列车-轨道耦合系统产生更大的振动响应;刘欢[18]利用SIMPACK建立了列车-轨道的刚柔耦合动力学模型,研究了典型车轮多边形磨耗阶次、幅值和运行速度对轮轨力和振动响应的影响。在车轮多边形磨耗噪声影响方面,韩铁礼等[19]通过跟踪测试车轮多边形发展和转向架区域振动噪声,研究了车轮多边形磨耗对列车转向架区域噪声的影响规律。

上述对车轮多边形磨耗的形成机理、对列车动力响应影响规律等研究均针对列车-轨道耦合系统,还未有文献在车桥耦合系统中考虑车轮多边形磨耗的影响。此外,在上述研究中有部分未考虑轨道不平顺的作用,这与列车实际的运营状态不符。当列车以一定速度通过桥梁时,列车质量沿桥跨的移动会改变桥梁结构的自振特性,由于轨道不平顺、机车车辆质量的不完全对中、各部件制造的不准确以及轮轨缺陷等因素,运动的车辆、轨道、桥梁会发生耦合振动[20]。而车轮多边形磨耗所产生的振动可能使桥梁的振动更加剧烈,而桥梁振动又反过来对车辆和轨道结构的振动产生影响,使桥上列车运行的安全性、平稳性以及桥梁结构运营的安全性进一步恶化。因此,对车轮多边形磨耗作用下车桥耦合振动的规律展开研究,为保障桥上列车的安全、平稳运行以及桥梁结构的安全运营提供参考。

1 车桥耦合动力学模型

1.1 列车多体动力学模型

基于多体动力学理论,以国内某高速列车拖车车辆为原型,运用专业的多体动力学分析软件SIMPACK建立了相应的多体动力学模型。模型中车体、转向架、轮对、轴箱等均考虑为刚体。列车的一、二系减振器采用弹簧阻尼元件进行模拟,并考虑了减振器的非线性特性。列车主要参数如表1所示。

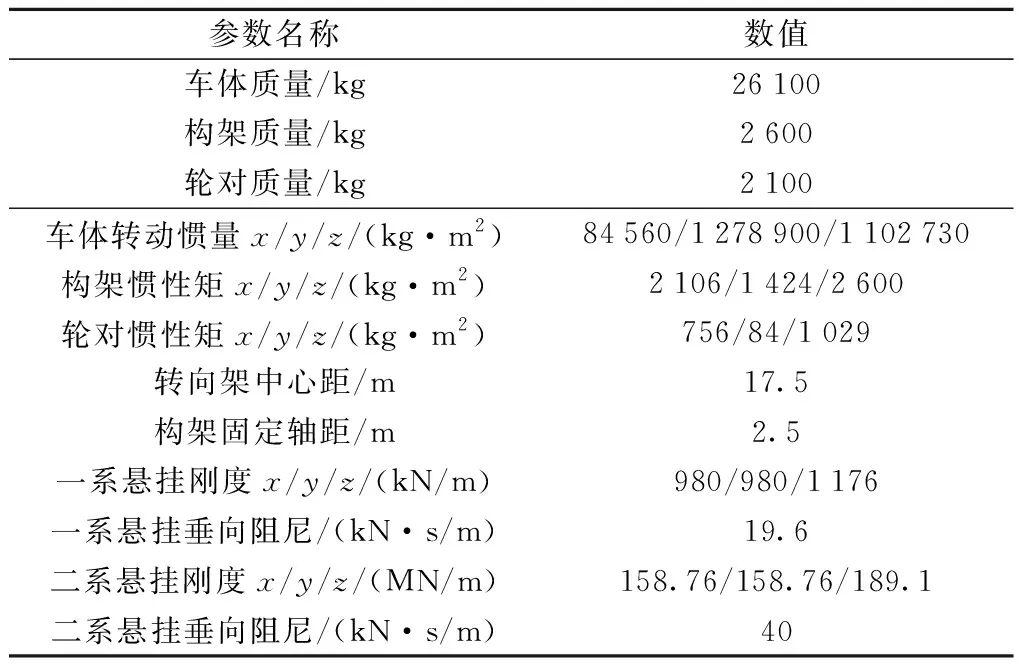
表1 列车模型主要参数Table 1 Main parameters of train model

1.2 桥梁、轨道有限元模型

用有限元分析软件ANSYS分别建立文献[21]中国内某高速铁路单跨32 m双线简支梁桥和CHN60型钢轨的有限元模型,单元类型均采用Beam188单元。考虑列车在桥梁左线行驶。轨道为CRTSⅠ型双块式无砟轨道,假定轨道板与桥梁连接牢靠,不对轨道结构振动做贡献,将道床板视为桥梁的参振质量,按二期恒载施加于主梁上。具体截面和材料参数分别如图1和表2所示。

图1 箱梁截面(单位:mm)Fig.1 Box girder section(unit: mm)

表2 桥梁、钢轨和扣件主要参数Table 2 Main parameters of bridge, rail and fastener

多体动力学分析软件SIMPACK与有限元软件联合仿真主要通过读取有限元模型的质量、刚度、阻尼以及模态矩阵实现,并通过模态综合法计算有限元模型的动力响应[22]。采用Guyan模态缩减法对桥梁有限元模型进行子结构分析,生成SIMPACK能识别的结果文件,在不影响计算精度的情况下,尽量缩减模型的自由度。ANSYS得到的桥梁模态和桥梁导入SIMPACK后的模态对比如表3所示,限于篇幅,本文仅给出了3阶车轮多边形磨耗对应频率附近的高阶模态来验证ANSYS模态缩减结果的正确性,其中简支梁桥主梁和桥墩的横向弯曲模态如图2所示。

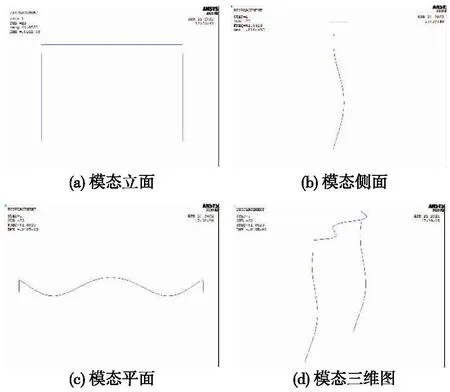
图2 主梁和桥墩的横向弯曲Fig.2 Lateral bending of main girder and piers

表3 高阶模态信息对比 HzTable 3 Comparison of high-order modal information

从表3可以发现,ANSYS模态分析结果与导入SIMPACK后的桥梁模态误差最大不超过0.25%,即自由度缩减后的模型不会影响计算精度,表明桥梁有限元模型的主自由度选择合理。

1.3 车桥耦合模型

建立车桥耦合模型的关键是实现列车和桥梁作用力的耦合。利用SIMPACK自带的柔性轨道模块,实现列车和钢轨之间作用力的耦合,进一步完成轮轨接触设置,从而建立列车-钢轨耦合模型。其中轮轨法向力采用Hertz理论计算,蠕滑力则采用FASTSIM算法求得。然后,通过弹簧阻尼力元模拟钢轨扣件实现钢轨和简支梁桥的连接,而桥墩和地面的连接则用大刚度弹簧模拟固结约束。为验证本文模型建立方法的正确性,以车速250 km/h过桥为例,对比了ANSYS静力过桥瞬态分析与SIMPACK车桥耦合振动分析时桥梁跨中竖向最大位移,结果如表4所示。

表4 计算结果对比Table 4 Comparison of calculation results

由表4可知,ANSYS静力过桥瞬态分析与SIMPACK车桥耦合振动分析的计算结果吻合较好,证明了本文中模型建立方法的正确性。车桥耦合模型如图3所示。

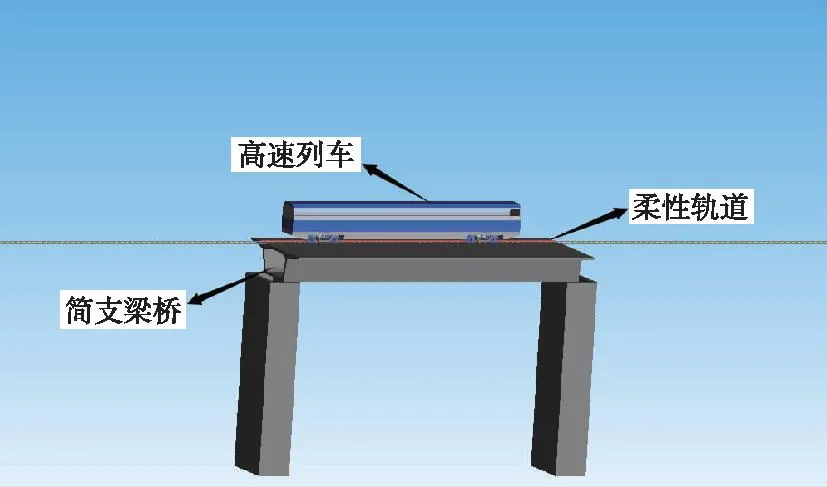
图3 车桥耦合模型Fig.3 Rail vehicle-bridge coupling model

2 车桥耦合系统的输入激励及其影响规律

2.1 车轮多边形磨耗

车轮多边形磨耗是车轮圆周在不均匀磨耗等因素作用下形成的周期性轮径偏差,可由式(1)的傅里叶级数形式表示[3]。

(1)

式中,ΔR(β)为轮径偏差;Ai为第i阶车轮多边形幅值;βi为第i阶车轮多边形初始相位角。

理想的列车车轮即使刚经过镟修或在镟修后较短的运行里程内,都有可能被检测出初始多边形磨耗[7]。1阶车轮多边形磨耗是由车轮安装或加工造成的偏心,3阶车轮多边形磨耗是由制造过程中三角爪固定方式造成的三角化,2阶和4阶车轮多边形磨耗分别表示车轮的椭圆化和四边化[13]。这种初始车轮多边形磨耗会随着列车运行里程增加而发展。而初始低阶车轮磨耗产生的振动频率相对较低,更加接近简支梁桥的振动频率,将会对车桥耦合系统的振动产生更大的影响。因此,本文主要探究低阶的初始车轮多边形磨耗对车桥耦合系统的影响规律。车轮多边形磨耗在SIMPACK中用非恒定半径的车轮进行模拟,即车轮的公称半径随车轮旋转角度而变化,通过Untrueness模块完成设置。图4展示了1～4阶车轮多边形磨耗的极坐标示意。

图4 车轮多边形磨耗示意Fig.4 Diagram of polygon wear of wheels

2.2 轨道不平顺

轨道不平顺是由于在铁路线路的平直段,钢轨并不是呈理想的平直状态,两根钢轨在高低和左右方向相对于理想的平直轨道存在偏差,这种几何参数的偏差即为轨道不平顺。我国高速铁路总体技术条件建议对列车进行平稳性分析时使用德国高速线路轨道谱。因此,本文的轨道不平顺谱选用适用于高速铁路线路的德国低干扰谱,采用三角级数法对高低不平顺、方向不平顺和水平不平顺的不平顺序列进行模拟,原理如式(2)所示。

(2)

式中,f(x)为模拟得到的轨道不平顺序列;S(ωk)为功率谱密度函数;ωk为轨道不平顺的空间频率;φk为第k个频率的相位,是独立均布于0～2π的随机数。

由三角级数法模拟得到的垂向轨道不平顺功率谱密度与德国低干扰谱吻合较好,如图5所示。

图5 模拟谱与目标谱垂向不平顺对比Fig.5 Vertical irregularity comparison of simulated spectrum with target spectrum

2.3 不同输入激励对耦合系统振动响应的影响

为分析车轮多边形磨耗对车桥耦合系统的影响,对比了仅以轨道不平顺作为输入激励时和同时把轨道不平顺和车轮多边形磨耗(阶数为3阶,幅值为0.04 mm)作为输入激励时耦合系统动力响应的差异。列车的平稳性指标、桥梁跨中和钢轨中点的竖向位移如分别图6、图7所示,其中钢轨中点是指桥梁跨中位置处对应的钢轨节点,后文的钢轨测点均为该位置。

图6 列车平稳性指标对比Fig.6 Comparison of train stability index

图7 桥梁跨中和钢轨中点竖向位移Fig.7 Vertical displacements at mid-span of bridge and rail

由图6可知,车轮多边形磨耗对列车运行的平稳性几乎无影响,这是因为车轮多边形磨耗的频率一般较高,超出了列车平稳性指标敏感范围,与文献[10]和文献[13]结果一致。由图7可知,桥梁跨中和钢轨中点的竖向位移随列车运行速度的提升总体呈现上升趋势但并非单调递增,车轮多边形磨耗对桥梁跨中竖向位移几乎无影响,但会使钢轨中点竖向位移略微增大。

列车以200 km/h速度运行时,不同输入激励作用下列车的轮重减载率、桥梁跨中和钢轨中点的振动加速度分别如图8～图12所示。

图8 轮重减载率对比Fig.8 Comparison of the wheel unloading rate

图9 桥梁跨中横向加速度响应对比Fig.9 Comparison of lateral acceleration response at mid-span of bridge

图10 桥梁跨中竖向加速度响应对比Fig.10 Comparison of vertical acceleration response at mid-span of bridge

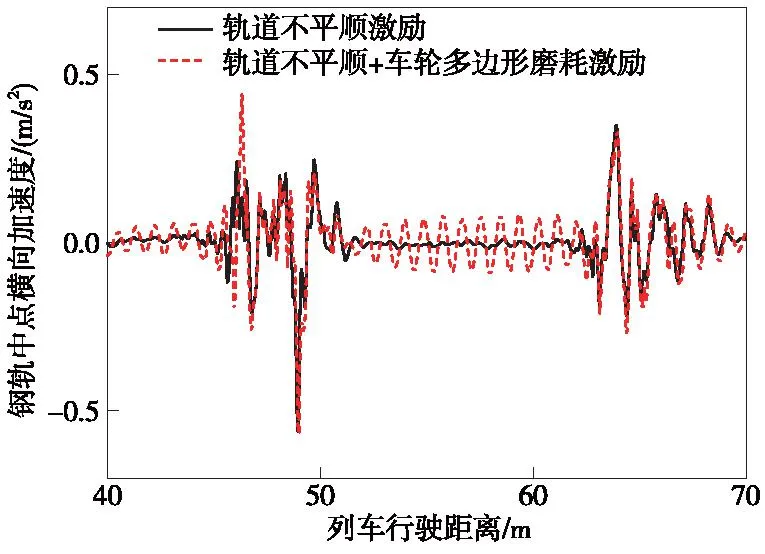
图11 钢轨中点横向加速度响应对比Fig.11 Comparison of lateral acceleration responce at mid-span of rail

图12 钢轨中点竖向加速度响应对比Fig.12 Comparison of vertical acceleration responce at mid-span of rail

由图8～图12可知,轮重减载率在仅具有轨道不平顺时的最大值为0.31,而有车轮多边形磨耗共同作用时的最大值为0.52。相对于仅具有轨道不平顺作用时的工况,车轮多边形磨耗使得列车的轮重减载率最大值增大了67.7%,这将降低列车运行的安全性。有车轮多边形磨耗共同作用时,桥梁跨中的横向和竖向振动加速度最大值分别为仅具有轨道不平顺作用时的2.74倍和2.27倍,桥梁的振动加速度显著增大。车轮多边形磨耗还使钢轨中点的横向和竖向振动加速度最大值相对于仅具有轨道不平顺作用时分别增大了26.4%和85.4%。由图12可以发现,钢轨中点的竖向加速度由于车轮达到时间的不同存在4个明显的峰值。综上所述,车轮多边形磨耗对车桥耦合系统的振动响应影响显著,针对车轮多边形磨耗对车桥耦合系统振动响应的影响规律展开研究是十分有必要的。

3 车轮多边形磨耗对车桥耦合系统的影响规律研究

轨道不平顺激励是随机的,这也使得车桥耦合系统的动力响应是典型的随机过程。随机轨道不平顺即使叠加了车轮多边形磨耗,车桥耦合系统动力响应的计算结果也仅是随机过程的一次实现,只代表车桥系统随机响应的某一个样本。为详细探究车轮多边形磨耗对车桥耦合系统的影响规律,对比分析了不同阶数、幅值的车轮多边形磨耗和相同轨道不平顺共同作用下,车桥耦合系统的列车轮重减载率、桥梁跨中和钢轨中点的横向和竖向振动加速度等指标的变化规律。

3.1 车轮多边形磨耗幅值的影响

为探究车轮多边形磨耗幅值对车桥耦合系统振动响应的影响规律,设定列车运行速度为200 km/h,车轮多边形磨耗阶数为3阶、幅值为0.02～0.08 mm,得到的耦合系统振动响应结果如图13～图17所示。

图13 不同幅值磨耗作用下列车轮重减载率响应Fig.13 Wheel unloading rate response with different amplitudes of polygon wear of wheels

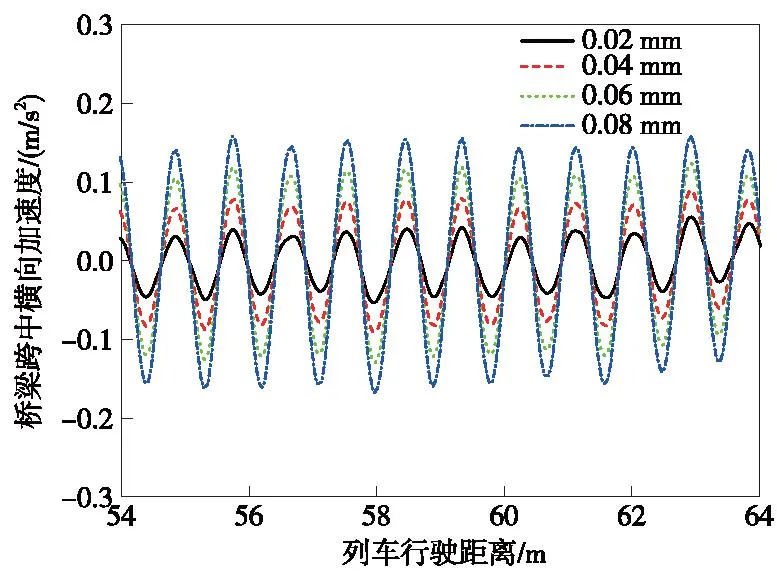
图14 不同幅值磨耗作用下桥梁跨中横向加速度响应Fig.14 Lateral acceleration responce at mid-span of bridge with different amplitudes of polygon wear of wheels

图15 不同幅值磨耗作用下桥梁跨中竖向加速度响应Fig.15 Vertical acceleration responce at mid-span of bridge with different amplitudes of polygon wear of wheels

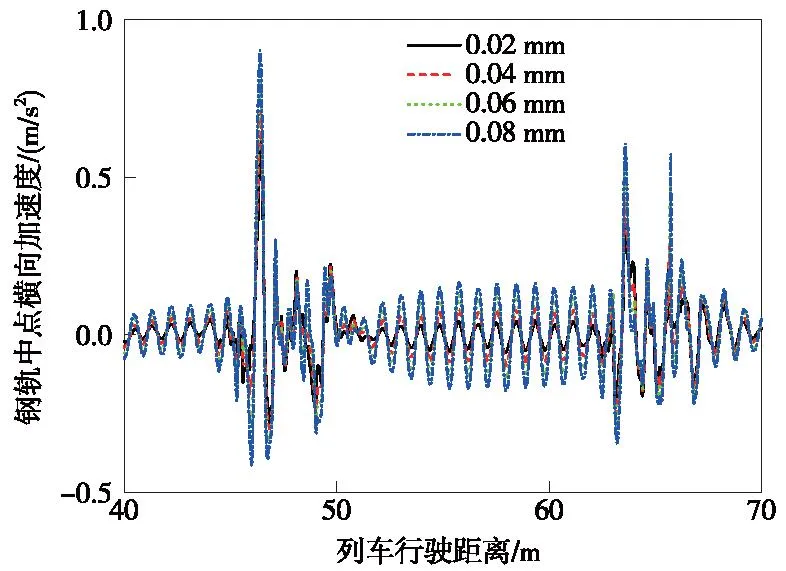
图16 不同幅值磨耗作用下钢轨中点横向加速度响应Fig.16 Lateral acceleration responce at mid-span of rail with different amplitudes of polygon wear of wheels

图17 不同幅值磨耗作用下钢轨中点竖向加速度响应Fig.17 Vertical acceleration responce at mid-span of rail with different amplitudes of polygon wear of wheels

由图13～图17可知,随着车轮多边形磨耗幅值增大,列车轮重减载率、桥梁跨中和钢轨中点的振动加速度增大;车轮多边形磨耗幅值由0.02 mm增大至0.08 mm,使列车的轮重减载率增大了76.5%,钢轨中点的横向和竖向加速度最大值分别增大了47.3%和83.1%;而车轮多边形磨耗幅值为0.08 mm时,桥梁跨中的横向和竖向加速度最大值是幅值为0.02 mm时的2.76倍和2.42倍。随着列车运营里程增加,车轮多边形磨耗的幅值也将随之增加,这将使得车桥耦合系统的振动更加剧烈,甚至可能会威胁到行车安全。

3.2 车轮多边形磨耗阶数的影响

为探究车轮多边形磨耗阶数对车桥耦合系统的影响,把1～4阶车轮多边形磨耗和轨道不平顺作为系统的输入激励,列车运行速度为200 km/h,车轮多边形磨耗幅值为0.04 mm。列车轮重减载率、桥梁跨中和钢轨中点的横向和竖向振动加速度分别如图18～图22所示。

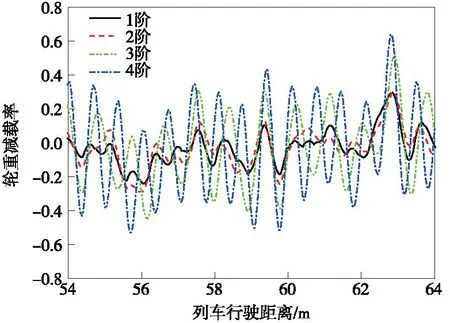
图18 不同阶数磨耗作用下列车轮重减载率响应Fig.18 Wheel unloading rate responce with different orders of polygon wear of wheels

由图18～图22可知,随着车轮多边形磨耗阶数增加,列车轮重减载率、桥梁跨中和钢轨中点的振动加速度均随之增大。4阶车轮多边形磨耗作用时,列车轮重减载率最大值、桥梁跨中竖向加速度最大值、钢轨中点的横向和竖向加速度最大值分别为1阶车轮多边形磨耗作用时的2.16倍、4.89倍、1.82倍和2.7倍。特别地,由图19可知,3阶车轮多边形磨耗作用下桥梁跨中的横向加速度增大显著,甚至远大于4阶车轮多边形磨耗作用下的振动响应。对3阶车轮多边形磨耗作用下的轮轨作用力和桥梁跨中横向加速度响应进行频域分析,结果如图23和图24所示。

图19 不同阶数磨耗作用下桥梁跨中横向加速度响应Fig.19 Lateral acceleration responce at mid-span of bridge with different orders of polygon wear of wheels

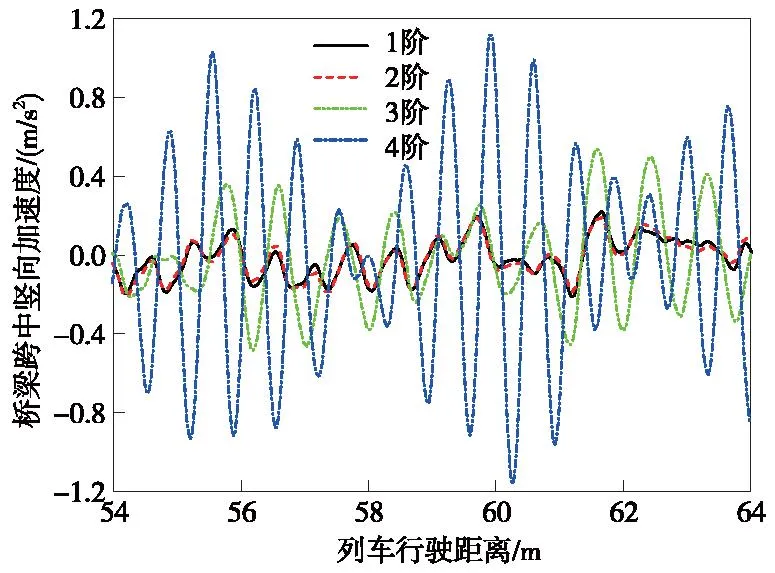
图20 不同阶数磨耗作用下桥梁跨中竖向加速度响应Fig.20 Vertical acceleration responce at mid-span of bridge with different orders of polygon wear of wheels

图21 不同阶数磨耗作用下钢轨中点横向加速度响应Fig.21 Lateral acceleration responce at mid-span of rail with different orders of polygon wear of wheels

图22 不同阶数磨耗作用下钢轨中点竖向加速度响应Fig.22 Vertical accelerations at mid-span of rail with different orders of polygon wear of wheels

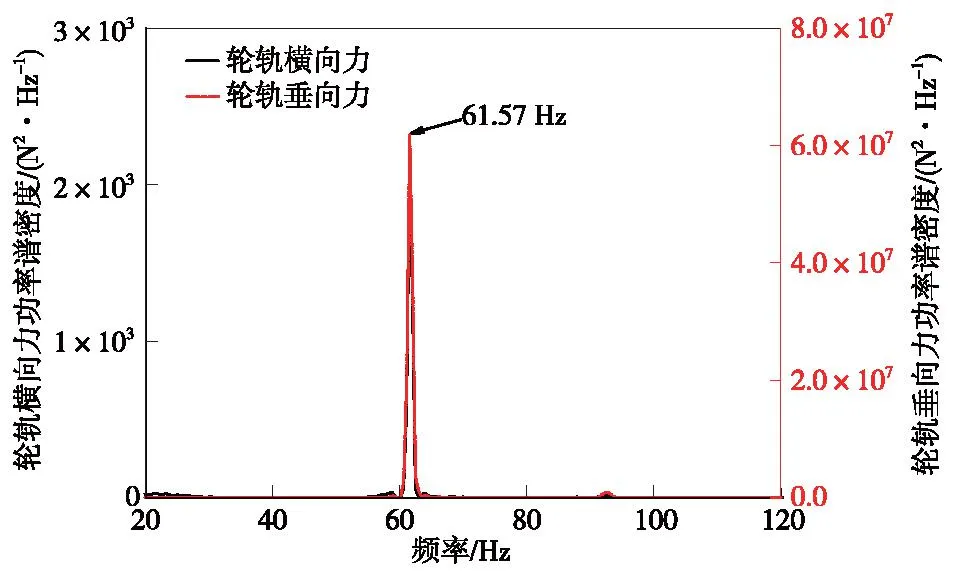
图23 轮轨作用力频域分析结果Fig.23 Frequency domain analysis results of wheel-rail force

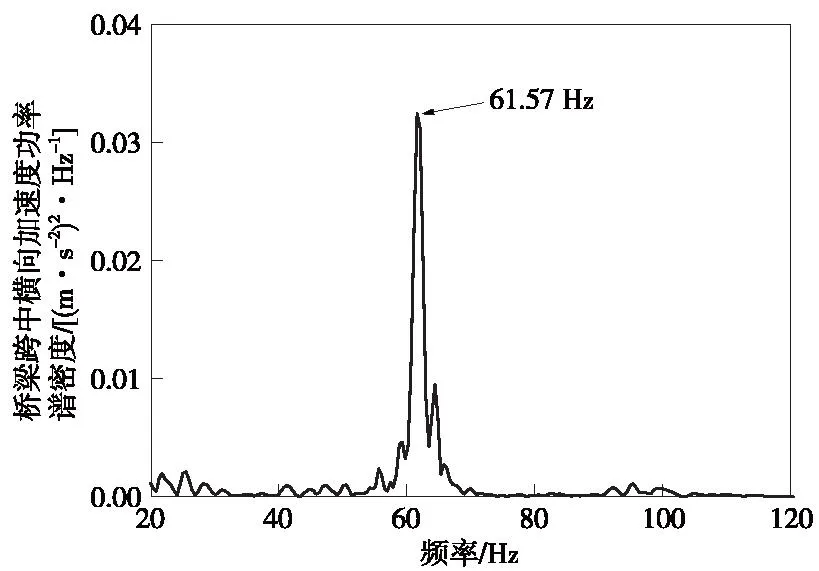
图24 桥梁跨中横向加速度频域分析结果Fig.24 Frequency domain analysis results of lateral accelerations at mid-span of bridge

由图23和图24可知,3阶车轮多边形磨耗引发的列车轮轨作用力频率为61.57 Hz,和桥梁跨中横向加速度响应的峰值频率相同。而该简支梁桥在61Hz频率附近存在横向振动模态(表3和图2)。因此,可以认为3阶车轮多边形磨耗引发的桥梁振动频率和桥梁的横向自振频率相近,从而引发桥梁横向共振,使得桥梁横向加速度显著增大。综上所述,高阶车轮多边形磨耗引起的车桥耦合振动响应更大,但某些阶数的车轮多边形磨耗可能引发桥梁共振使得桥梁的振动响应显著放大,可能对车桥耦合系统安全性和结构耐久性造成影响。

4 结论

为探究车轮多边形磨耗对车桥耦合振动响应的影响规律,为保障具有车轮多边形磨耗的高速列车安全运营提供参考。首先,基于ANSYS和SIMPACK联合仿真的方法建立了车桥耦合模型;然后,以不同输入激励研究了车轮多边形磨耗对耦合系统的影响程度;最后,探究了不同幅值、阶数的车轮多边形磨耗和轨道不平顺共同作用时车桥耦合系统振动响应的影响规律,得出如下结论。

(1)车轮多边形磨耗对车桥耦合系统的振动响应影响显著。3阶车轮多边形磨耗使车轮轮重减载率最大值增大67.7%,严重降低了列车运行的安全性,也使桥梁跨中横向和竖向加速度最大值分别增大2.74倍和2.27倍。

(2)车轮多边形磨耗幅值增大使车桥耦合系统的振动响应显著增大。车轮多边形磨耗幅值由0.02 mm增大至0.08 mm时,列车轮重减载率、桥梁跨中横向和竖向加速度、钢轨中点横向和竖向加速度分别增加76.5%、174%和127%、47.3%和83.1%。随着列车运营里程增加,车轮多边形磨耗幅值将随之增加,这可能会使得车桥耦合系统的振动进一步加剧,降低列车运行的安全性和桥梁结构的耐久性。

(3)车轮多边形磨耗阶数增加也会使车桥耦合系统的振动响应显著增大。车轮多边形磨耗阶数由1阶增大至4阶时,列车轮重减载率、桥梁跨中竖向加速度、钢轨中点横向和竖向加速度分别增加116%、389%、82.0%和170%。特别地,列车以200 km/h速度运行时,3阶车轮多边形磨耗引发桥梁横向共振使得桥梁跨中横向加速度显著增大,是4阶车轮多边形磨耗作用时的2.74倍。