刚性与柔性边界下砂离散元三轴试验力学特性对比分析

陈爱平，刘凯文，邱睿哲，熊志鹏，蔡志清

(1.成都工业职业技术学院轨道交通学院,成都 610218; 2.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031;3.西南交通大学土木工程学院,成都 610031; 4.贵阳中天岩土工程有限公司,贵阳 550001)

引言

在三轴试验中,对具有代表性的土体材料试样通过控制沿试样边界的力/压力或位移,可获得试样相关的力学特性参数。其中,材料的位移变化响应与应力大小有关;而材料膨胀或收缩的趋势则由其密度和应力水平决定[1]。目前,已有学者在室内三轴试验方面进行了土体的特性研究[2-5]。然而,受限于目前已有的观测技术水平,难以在细观尺度上观测土体试样内部的位移变形特性[6]。

离散元方法(discrete element method,DEM) 不仅可以节约物力、人力的成本,还能多次重复同一模型试验并克服传统的宏观连续性假设。大量学者开展基于离散元的数值模拟研究[7-10]。颗粒流模型细观参数的确定是离散元数值模拟研究的关键环节,因此基于颗粒流的三轴试验研究尤为重要[11]。CHENG等[12]较早地提出将DEM应用于三轴试验的模拟分析中,发现这种数值模型的塑性行为与真实的砂土非常相似。随后,一批学者开始选择采用颗粒流软件建立三轴模型对砂土[13-14]、黏土[15-16]的细观参数进行分析。结果表明,颗粒粒径大小和孔隙率是影响砂土压缩特性的重要参数,孔隙率、黏结强度和摩擦系数等是影响黏土宏观力学性质的重要参数,并基于这些结论建立了颗粒细观参数与宏观力学指标之间关系[17]。尽管这些研究在帮助理解土体材料细观参数与宏观力学特性关联机制上取得进展,但其结果仍与真实三轴试验存在差异。因此,如何采用离散元方法更为合理地再现三轴试验成为重要话题。当前相关研究主要采用刚性边界墙作为伺服边界,并结合边界控制系统来控制应力[18],这种方法可以简单有效地用于控制沿边界的整体应力状态。然而,CHEUNG等[19]认为,如果模拟一个局部发展的三轴压缩试验,这些刚性边界将抑制这个局部剪切带的自然发展,并且沿边界施加的应力将存在显著的不均匀性。因此,其提出了使用一种“应力控制膜”来模拟包裹样品的柔性乳胶膜伺服模拟方法。

目前采用围压柔性加载的三轴试验离散元模拟还较少,不同边界加载围压下三轴砂土试样的力学特性、变形特性以及变形破坏规律也尚未探明。为此,利用PFC6.0程序开展不同密实度的HST95标准砂三轴模型试验模拟,并结合试验数据讨论不同围压加载方式下DEM三轴试验模型合理性,从颗粒细观尺度上对比分析了不同边界加载方式下砂土试样剪切带的形成、发展过程。

1 模型基本参数

1.1 砂土颗粒生成

本文采用的DEM模拟模型中砂土是基于英国邓迪大学一系列岩土试验采用的HST95标准砂土[20],该砂土基本物理参数如表1所示。

表1 HST95砂土物理参数Table 1 Physical parameters of HST95 sand

为使DEM中生成的颗粒与砂土实际级配一致,依据土体级配曲线将颗粒划分为多组,后采用随机分布颗粒生成法在区域范围内随机生成目标孔隙率的颗粒,得到颗粒级配如图1所示。由图1可知,其级配分布情况与实际情况基本吻合。

图1 离散元颗粒级配与砂土级配Fig.1 Gradation of discrete element particle and sand

1.2 DEM模型建立

采用如下方法建立三维HST95砂土DEM模型,模型砂土体采用ball球体单元进行模拟,该方法主要包括以下步骤。

(1)土体成样。于DEM模型尺寸边界生成刚性墙体,在设定的刚性墙体内采用随机分布颗粒生成法生成目标孔隙率的级配颗粒,然后将接触模型及各类参数赋值在颗粒与墙体间,再通过循环命令使得颗粒之间逐渐降低不平衡力,使颗粒稳定。

(2)边界模拟。对平衡完毕的试样颗粒进行边界伺服,对于刚性边界条件下:采用循环伺服机制对侧向墙体的移动速度进行调整,以达到目标所需围压值。对于柔性边界条件下:将侧向刚性墙替换为由球体颗粒组成的“柔性墙体”,再通过边界命令来控制调整边界球体颗粒上的集中力,从而实现与实际物理三轴试验相同的柔性围压。

(3)模型加载。清除上下边界墙体的边界状态,保持侧向围压的边界状态,对上下墙体施加一个恒定压缩速度进行加载。随加载过程记录试样的应力-应变曲线、孔隙率、体应变和位移变化云图等宏、细观参数,以供后续进行参数分析。

图2为刚性和柔性边界条件下颗粒试样模型边界状态时的剖面,即边墙与颗粒的分布情况。

图2 不同边界条件下模型剖面Fig.2 Model section under various boundary conditions

2 DEM加载模拟原理

2.1 柔性边界模拟

在DEM三轴试验模拟中,刚性边界模拟通常只需建立刚性墙体即可快速实现。而为讨论柔性边界对三轴试验仿真模拟的影响,文中柔性边界采用大小相同的球体颗粒组成球体膜颗粒来模拟三轴物理试验中的柔性膜。模型中柔性膜颗粒是由每层相互平行排列的颗粒圆组成,颗粒间彼此接触黏结,相邻颗粒间形心距离为L(两倍的膜颗粒半径r)。因三轴试验中橡皮膜的特殊柔软力学特性,故将膜颗粒间设置为不传递力矩的接触-黏结模型进行模拟。具体模型和接触示意如图3所示。

图3 柔性膜颗粒示意Fig.3 Schematic diagram of flexible membrane particles

2.2 围压边界原理

在刚性边界三轴试验模拟过程中,围压通过刚性墙进行加载,限制试样发生同步侧向变形。在柔性边界三轴试验模拟过程中,围压则需通过等效集中力的方式施加在球体膜颗粒上,从而无需强迫发生同步侧向变形,在每一次边界循环过程中进行集中力的计算判断,根据膜颗粒的相对位置不断调整至所有试样球体颗粒-膜颗粒平均应力达到目标值。对于柔性膜颗粒而言,任意球体颗粒皆与周围颗粒接触在一起。图4为膜颗粒集中力的计算示意。

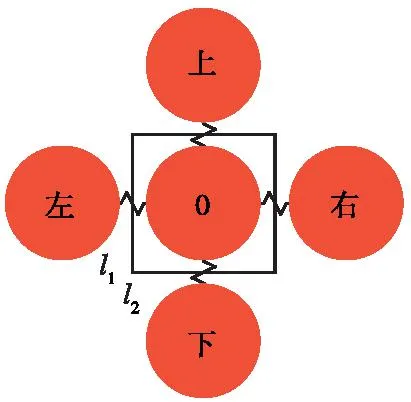
图4 膜颗粒等效力计算示意Fig.4 Calculation of equivalent force for membrane particles

对于任意一个膜颗粒,施加在该颗粒的等效集中力计算公式如下

F=Aσ

(1)

式中,F为集中力;A为等效面积;σ为控制围压。其中,等效面积的计算公式如下

A=l1×l2

(2)

式中,l1,l2分别为与球体相切四边形相邻两边长的向量。

2.3 试样颗粒接触模型

根据上述过程建立三维DEM三轴试验模型,对土体颗粒进行参数赋值,参数接触采用赫兹非线性模型。该接触模型适用于光滑的弹性散体材料,也是DEM软件中适用于分析砂土颗粒特性的接触模型。赫兹接触模型基于Mindlin和Deresiewicz(1953)[21]的近似理论得到的非线性公式组成。赫兹接触模型产生法向力和剪切力是基于对光滑弹性球体在摩擦接触中的变形理论分析。

赫兹模型中,接触力可分解为赫兹分量和阻尼分量,赫兹分量部分提供线弹性行为,阻尼分量部分提供黏性行为。接触力的计算关系公式为

Fc=Fh+Fd

(3)

式中,Fh为非线性赫兹力;Fd为阻尼力。

本文DEM赫兹模型具体细观参数以Micheal(2019)模型所标定出的接触参数为标准[22],如表2所示,其主要包含的参数有:剪切模量S,摩擦系数fc,泊松比υ。

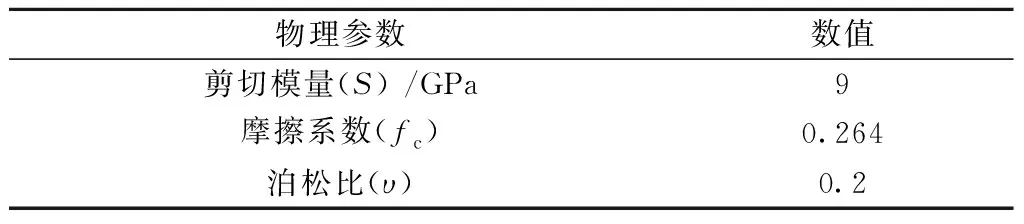
表2 DEM模型接触参数Table 2 Contact parameters of DEM model

3 DEM试验模拟分析

利用前文所述围压加载原理,分别对不同边界方式和密实度的HST95砂土建立60 kPa围压下三轴DEM模型,与文献[22]中试验结果数据对比分析不同边界加载方式的合理性,进而对HST95砂土试样力学特性、变形特性和剪切过程进行分析。

3.1 力学特性分析

图5给出了不同边界条件下模拟HST95砂土剪切破坏过程的应力应变曲线,分析图5可得到如下结论。

图5 不同密实度下应力应变曲线Fig.5 Stress-strain curves under different relative densities

(1)相较于柔性边界,刚性边界情况下应力曲线增长速度更快,应力峰值也更大。

(2)在4%左右应变对应的峰值应力上,30%密实度刚性边界、柔性边界的峰值应力为180.53 kPa和160.06 kPa,分别为试验数据的115.4%和102.6%;70%密实度刚性边界、柔性边界的峰值应力为255.26 kPa和236.92 kPa,分别为试验数据的107.8%和100.5%。

(3)在20%应变对应的残余应力数值上,30%密实度刚性边界、柔性边界的残余应力为148.15 kPa和134.15 kPa,分别为试验数据的110.9%和101.6%;70%密实度刚性边界、柔性边界的残余应力为220.55 kPa和154.52 kPa,分别为试验数据的153%和107.6%,刚性边界条件下的残余应力较大。由此表明,该DEM仿真模型能有效地模拟还原HST95砂土的室内三轴试验,柔性边界模型应力应变的发展过程与砂土实际的压缩过程更为接近,其能够更为有效地模拟出室内试验的效果。

3.2 变形特性分析

为准确分析三轴试样的变形特性,分别在柔性和刚性边界三轴模型中设置高度值为0.2、0.3、0.5、0.6和0.7倍试样高度,直径为0.9倍试样宽的5个测量球,如图6所示。通过测量球监测试样颗粒孔隙率的变化,分析不同边界条件下试样的变形特性。

图6 测量球分布示意(柔性左,刚性右)Fig.6 Distribution diagram of measurement ball (Left: flexible; Right: rigid)

图7给出了不同边界条件下三维模型的孔隙率变化曲线对比情况,可以得出如下结论。(1)在30%密实度条件下,孔隙率变化呈现逐渐减小至稳定的趋势。在数值上,20%应变时刚性边界和柔性边界的孔隙率分别为0.381和0.383。(2)在70%密实度条件下,不同边界条件对孔隙率变化的影响差别较大。刚性边界孔隙率变化呈现“先小幅度减小,再逐渐增大,后再次减小”的变化规律;柔性边界孔隙率变化与密砂的体应变变化规律一致,为“先剪缩,后剪胀”的特点。在数值上,20%应变时刚性边界和柔性边界的孔隙率分别为0.363和0.369。

图7 孔隙率变化对比Fig.7 Comparison of porosity changes

结合孔隙率对比情况,进一步分析试样的体积变形特性,图8给出了三维模型的体积应变曲线与模型试验对比情况,可以得出如下结论。(1)变形趋势上,柔性边界模型较好地体现出了“松砂剪缩,密砂剪胀”的砂土剪切变形规律;而刚性边界在70%密实度情况下与试验数据存在较大差异。(2)在数值上,20%剪切应变时30%密实度刚性边界和柔性边界的体应变为-6.4%和-6.2%,分别为试验数据的106.7%和100.6%;70%密实度刚性边界和柔性边界的体应变为1.9%和2.9%,分别为试验数据的67.9%和100.3%。(3)无论在何种密实度工况下,柔性边界模型的体积应变都与模型试验结果更为吻合。具体而言,30%低密实度条件下,体积应变均与试验一样,呈现“不断减小,逐步放缓”的特点,且柔性边界数据与试验更为接近。70%高密实度条件下,柔性边界体应变与试验数据吻合较好,表现为“先剪缩,后剪胀”的变化特点;而刚性边界条件下,体积应变则表现为“先剪缩,后剪胀,再剪缩”的趋势,其最后阶段的“剪缩”特征与实际试验存在较大误差。

图8 体积应变对比Fig.8 Comparison of volume strain

3.3 剪切破坏过程分析

柔性和刚性边界下试样颗粒的位移矢量如图9所示。当采用柔性边界时,70%密实度试样两侧出现明显的腰型鼓胀变形,变形特性与实际的三轴试验更为接近;而采用刚性边界时,试样的侧向鼓胀变形受到侧向刚性墙体的约束,其发展受限,侧向未发生明显的鼓胀变形。因此,柔性边界能够更为清楚地反映出三轴剪切过程中的侧向变形特性。

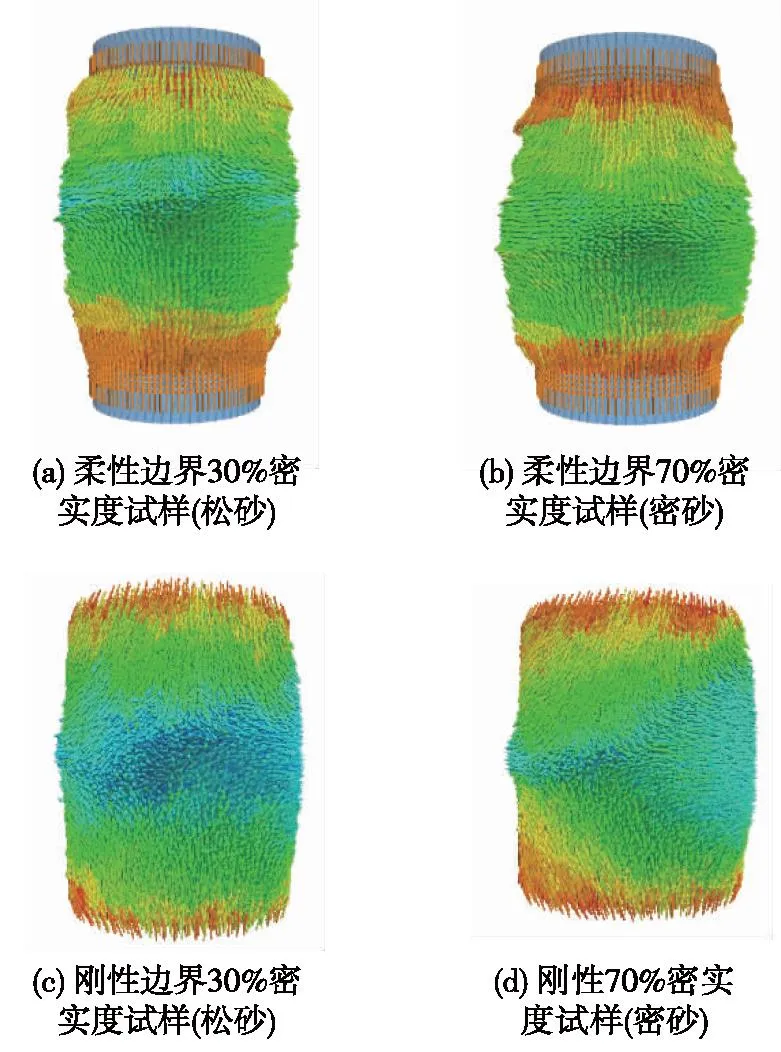
图9 试样中颗粒的位移矢量图Fig.9 Diagram of displacement vector for particles in samples

进一步选取不同密实度情况下,对各模型的加载过程进行切片,分析各边界条件下试样的剪切破坏特性与变形规律。相关研究中,颗粒材料破坏往往伴随着剪切带的形成。通过对加载过程中的HST95砂土模型试样进行切片后,根据试样外部的变形特性和内部颗粒的转动特征,分析HST95砂土试样破坏后形成的剪切带。

图10给出了各边界条件在5%、10%和20%相对密实度下,试样颗粒轴向应变的位移剖面云图。从图10中可以看出,各组模型均体现出三轴加载过程中剪切带的形成,说明模型能有效地还原土体试样的剪切破坏特性。随着轴向应变增加,试样的剪切带开始由局部形成,之后随着轴向应变继续发展。对比柔性和刚性边界的试样位移云图,柔性边界试样在剪切应变作用下开始出现侧向鼓胀变形,使得剪试样内位移云图进一步变化。由此可知,试样在轴向位移加载下,随着轴向应变增大,试样的剪切带会不断发展,且柔性边界会使剪切带进一步变化。对比30%和70%密实度的工况,可以发现在高密实度状态下,剪切破坏带发展更快。

图10 试样中颗粒轴向应变的位移云图Fig.10 Displacement nephogram of particles axial strain in samples

4 结 论

采用DEM软件PFC,基于赫兹非线性接触模型、刚性墙围压边界和柔性黏结颗粒膜的围压边界方法,开展了不同密实度下HST95标准砂试样的DEM三轴试验模拟,分析了不同边界条件对DEM模拟三轴试样的力学特性、变形特性和变形破坏规律,得出本试验特定条件下的结论。

(1)30%和70%密实度试样在刚性边界加载下,其结果与试验结果对比,误差在7%～53%区间,而柔性边界加载结果与试验结果对比误差均在10%以内, 对于相对密实度越大的试样,柔性边界加载对于三轴试验力学特性的还原程度越优于刚性加载。

(2)柔性边界加载“松砂剪缩硬化、密砂剪胀软化”的变化趋势与数值及室内试验结果基本一致,而刚性边界加载下密砂剪切应变超过12.5%后体应变呈现增大的变化趋势与试验不符。柔性边界加载下对于30%和70%密实度试样其20%剪切应变下的体应变与试验结果误差均在1%以内,而刚性边界加载下误差分别为6.7%和32.1%。对于相对密实度越大的试样,柔性边界加载对于三轴试验变形特性的还原程度越优于刚性加载。

(3)通过对剪切带形成过程分析发现,刚性和柔性边界条件下,模型均体现出了剪切破坏的特性,且在柔性边界状态下,随着应变继续增加,试样侧向不均匀鼓胀变形加剧,试样内部颗粒位移进一步变化,能更好反映剪切带的形成过程。