枝节直波导与开口方环耦合谐振腔的Fano谐振特性研究

赵小侠, 刘 晗, 贺俊芳, 李喜龙, 张云哲, 高雪艳, 刘 寒, 李院院

(西安文理学院 陕西省表面工程与再制造重点实验室, 西安 710065)

1 引 言

表面等离子体激元(Surface Plasmon Polaritons -SPPs)是由在金属导体表面由光子驱动自由电子相干共振，形成束缚在金属界面的电子密度波与电磁波能量耦合传输形成的特殊波动形式. 金属表面自由电子与入射光子相互作用形成一种沿金属与电介质表面传播的电磁波，其强度在远离金属-介质表面处呈指数衰减[1，2]. SPPs是一种TM偏振的表面波，能够突破光学的衍射极限，可以在亚波长范围内对电磁场进行调控与传输，可以实现纳米尺度的光信息传输与处理[3]. 特别是基于SPPs的MIM波导，具有较好的局域场增强特性和易于集成等优点使得其在高集成度光子电路中具有重要应用.

Fano共振[3-10]产生的典型非对称响应谱线形状，可以增大透射谱线的波谱分辨率. 近年来，MIM型波导凭借其有效的模场束缚及较低的传输损耗而成为SPPs较为理想的传输线路. 在MIM波导实现Fano共振，可以为微纳结构的折射率传感提供一种有效的选择方案. 目前MIM共振空腔的形状有：半圆形与矩形谐振腔耦合结构[4]；非对称双边凹槽结构[5]，对称双边凹槽耦合空腔结构[6]、单边侧耦合空腔结构[7]、T型空腔共振结构[8]，开口方环共振空腔耦合[9，10]，类云朵腔结构[11]等形状. 这些共振腔设计有的无法同时提供较高的敏感度及品质因数，有的共振结构虽然可以满足较高的敏感度及品质因数，但却不能实现共振模式的可控调节.

本文设计了枝节直波导与开口方环耦合谐振腔的波导结构. 文中采有限元分析法详细分析了枝节谐振腔高度对耦合波导透射谱线的影响，并计算出形成单反射峰的枝节谐振腔的最佳高度. 在波长1500 nm～1700 nm之间，通过设置最佳参数，经拟合计算得到该谐振耦合腔可以作为一个灵敏度S约为1496 nm/RIU，FOM=60.1的折射率传感器.

2 结构设计及传输特性

在入射电磁波频率在 1013<ω<1015Hz 范围时，红外光、可见光入射到金属表面，此时金属的相对介电常数是一个负数，折射率n 是一个虚数，这种情况下电磁波基本不进入金属内部，几乎全部被金属反射回去，金属显示出镜子般反射特性，此时金属与绝缘体没有本质区别[7]. 所有金属在这个光频段都可以产生SPPs，但贵金属材料(金、银等)具有更好的性能. 目前在SPPs研究中优先考虑的金属是银. 银的光学特性可以用相对介电常数来表现银的光学特性(见图1)，金属银介电常数的实部在本文所研究的波长范围内取值均为负数，并且可以激发出SPPs波，且随着波长的增加介电常数的实部呈下降的趋势.

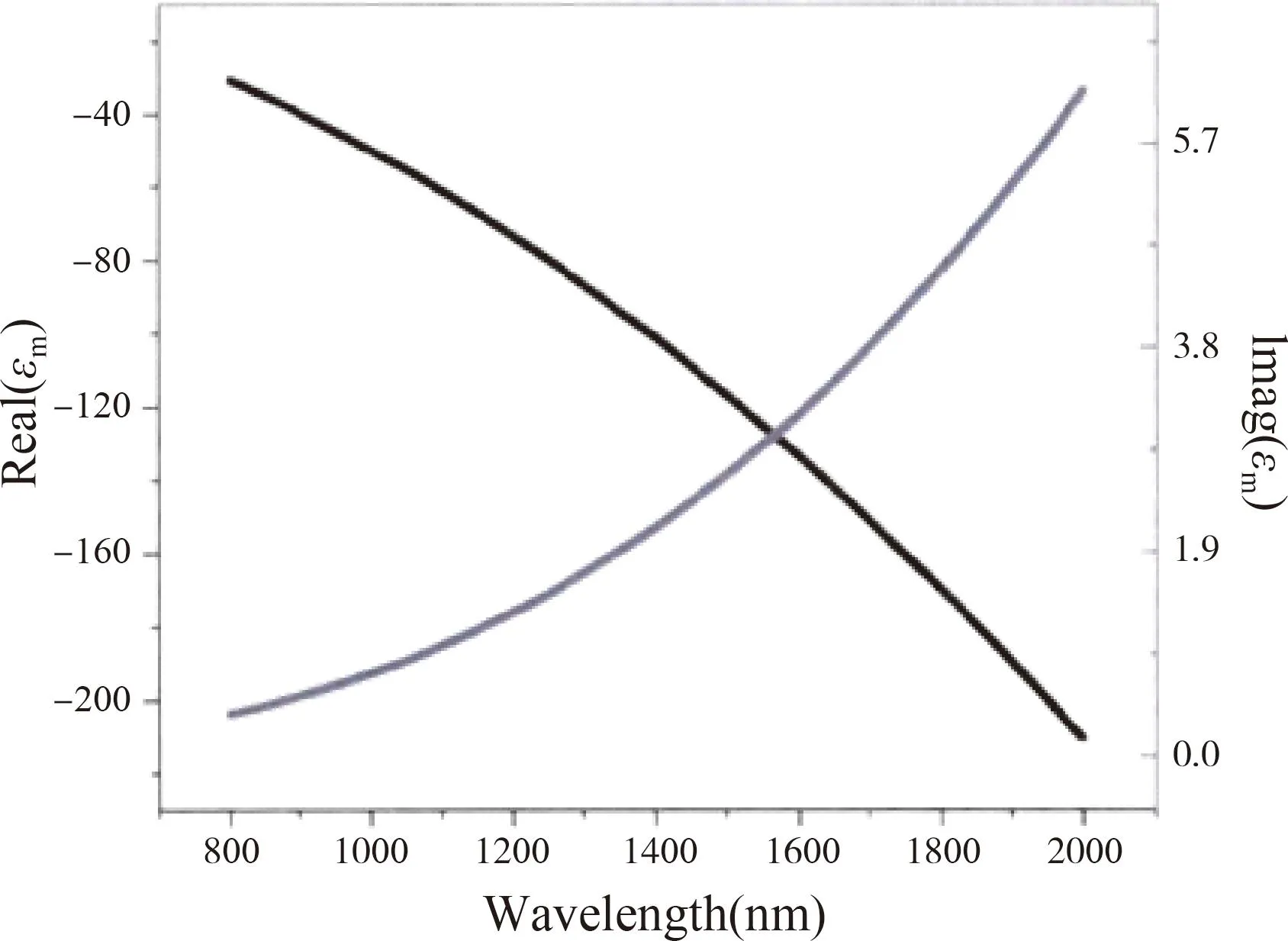
图1 银的相对介电常数实部(黑色实线)，虚部(蓝色实线)随工作波长的变化关系Fig. 1 The real part (black solid line)and imaginary part (blue solid line)of the relative permittivity of silver as a function of the operating wavelength

本文将研究MIM结构在TM0模式下形成的Fano谐振的表现，设置材料为金属银和介质空气，然后设置求解域、端口和边界条件、划分网格. 设置参数化扫描，使波长在600～1800 nm之间，构建带有枝节谐振腔的直波导，如图2左边所示，设置波导与枝节宽度W=50 nm，枝节谐振腔高度H=140 nm.

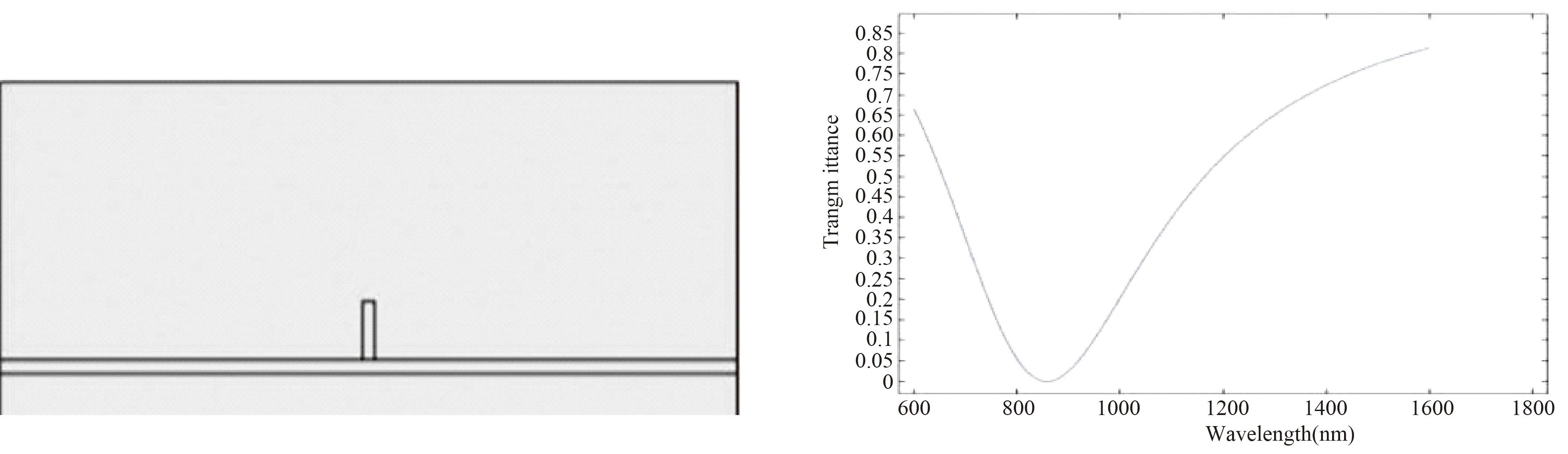
图2 枝节直波导结构(左边)及其传输谱(右边)Fig.2 Branch straight waveguide structure (left)and its transmission spectrum (right)

当入射光波从模型左侧端口边界入射，并最终从右侧端口出射. 不同波长的透射率计算公式为：

T=Pout/Pin

(1)

其中Pin为入射光功率，Pout为出射光功率. 可得到枝节直波导谐振腔的传输谱如图2右边所示，其为一较宽的连续谱.

构建带开口方环无枝节谐振腔与直波导如下图3左边所示，令总线波导与开口方环的宽度W=50 nm，方环外边长l=350 nm，方环开口的长度B=90 nm.

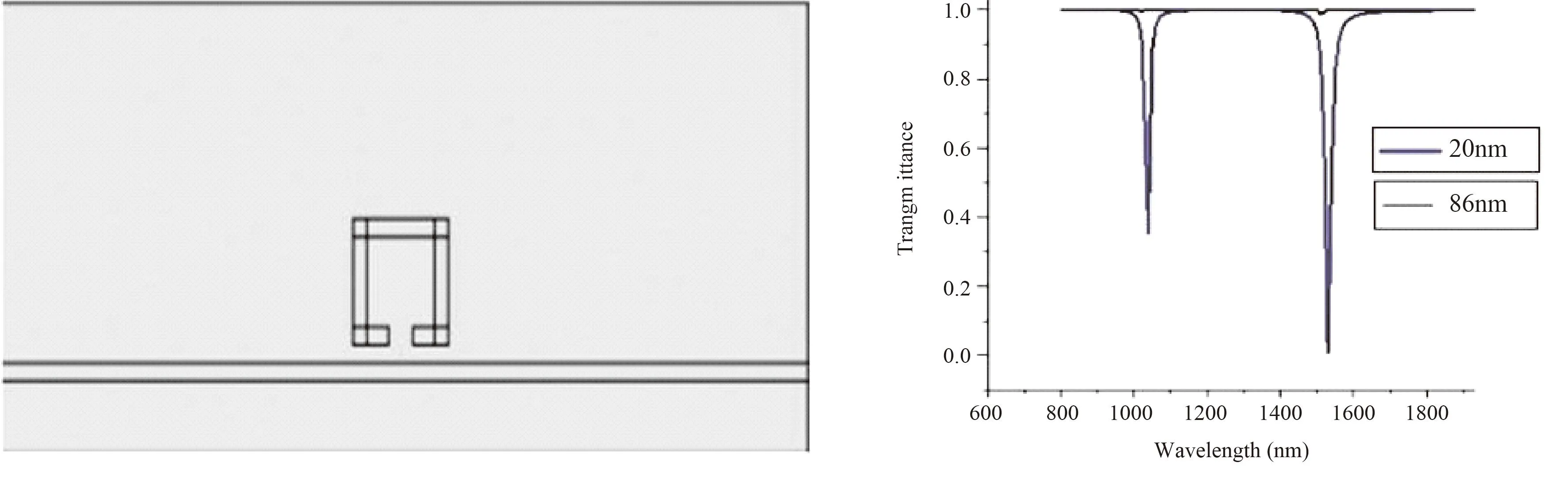
图3 开口方环与总线波导结构(左边)及其透过率随波长的变化图(右边)Fig.3 Open square ring and bus waveguide structure (left)and its transmittance as a function of wavelength (right)

为了实现有效的Fano谐振并保持光波传输过程中，总线波导中的电磁场能量不能与开口方环谐振腔发生直接耦合，需要合理设置开口方环和总线波导的间距G. 模拟得出不同G值时，开口方环的直波导传输谱如图3右边所示，是窄离散态的传输谱. 改变开口方环距离直波导的垂直位置G，使得传输谱的传输率变得越来越小，直至几乎完全消失，即直波导里的电磁波无法直接与开口方环耦合.

图3右边为开口方环的透过率随波长的变化图，横坐标表示波长，纵坐标表示为透射率. 图中蓝色曲线表示开口方环与直波导间距G= 20 nm时的透射率变化曲线，在波长为λ1=1039.11 nm时透射率约为0.361，当波长增大到λ2=1528.34 nm时，透射率为 0.007. 图中黑色线表示开口方环距离直波导的垂直位置G=86 nm时的透射率变化曲线，基本上为一条直线，说明耦合几乎消失，开口方环谐振腔不能直接被入射波激活.

基于以上研究，下文中设置开口方环与总波导间距G=90 nm，则开口方环谐振腔将不能被入射光波直接激发.

设置枝节高度H=140 nm，构建出开口方环与带枝节直波导耦合谐振腔模型如下图4左边所示.

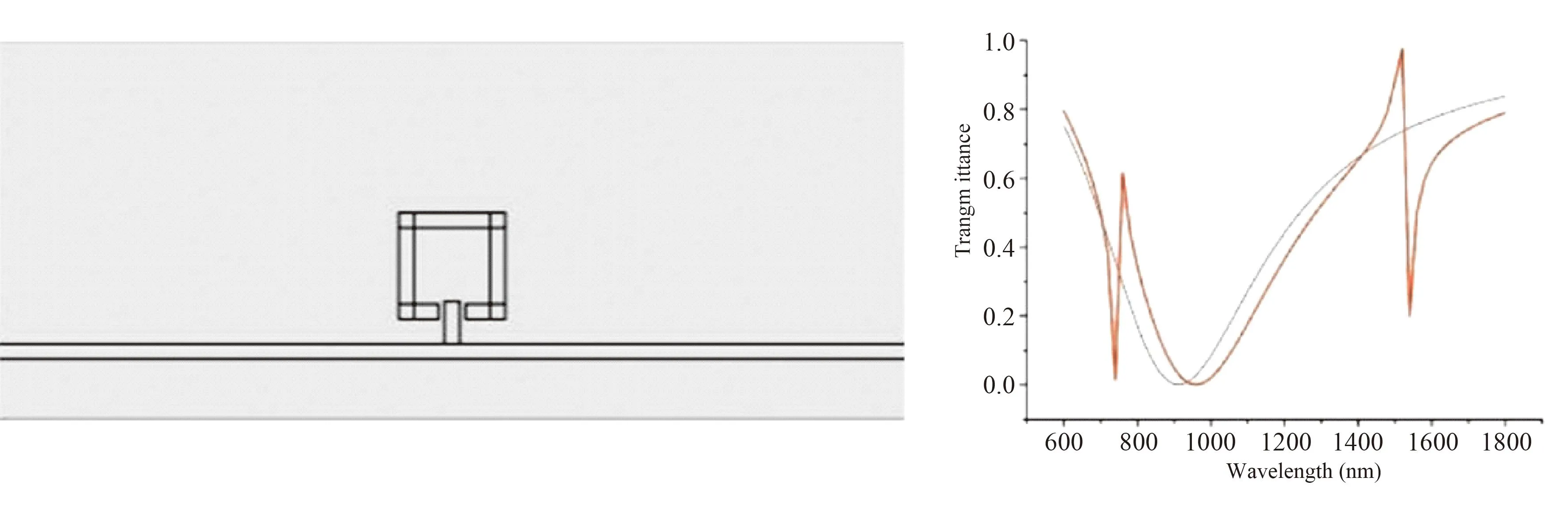
图4 开口方环与带枝节直波导谐振腔结构(左边)及其产生的传输谱(右边)Fig. 4 The open square ring and straight waveguide resonator structure with branches (left)and the resulting transmission spectrum (right)

图4右边中黑色实线为带枝节直波导的传输谱，红色曲线表示的是开口方环与带枝节直波导谐振腔耦合的传输谱. 由于枝节与直波导相连，可以轻易与直波导耦合，形成图中黑色与红色都有的传输谷，其有着很好的阻带特性，且该传输谷的阻带较宽，是一种连续态的传输状态，这种状态与开口方环的特定窄离散态发生耦合，形成如图4中右边红色曲线所对应的两个边沿陡峭的反对称透射峰的Fano谐振的曲线，Fano谐振反对称透射峰发生的位置大致在λ=746 nm和1521 nm.

为了探究Fano谐振透射谱变化的内在机理，找出图4中右边红色曲线传输谱中的拐点，即图中左侧传输波谷、左侧透射波峰、中间传输波谷、右侧透射波峰和右侧传输波谷分别对应波长λ=739 nm，746 nm，950 nm，1521 nm和1534 nm处的磁场分布如下图5所示.

由于中间传输波谷与图中黑色曲线的传输波谷即枝节的传输波谷相近，为了与Fano谐振产生的传输波谷区分，暂时将中间传输波谷称作枝节传输波谷. 由图5可以看出，在左侧传输波谷(λ=739 nm)处在直波导的前半段与枝节和开口方环存在大量能量，而直波导的后半段仅存在少量能量；在左侧透射波峰(λ=746 nm)处有大量磁场能量处于开口方环中，枝节上几乎不存在能量，直波导存在部分能量；在枝节传输波谷(λ=950 nm)处，发生了耦合现象，大量的磁场能量集中在直波导的前半段和枝节中，只有少量的能量存在于开口方环，直波导的后半段几乎没有能量；在右侧传射波峰(λ=1521 nm)处，能量分布几乎与左侧传输波峰相同；在右侧传输波谷(λ=1534 nm)处，磁场能量主要存在于开口环谐振腔内，直波导的前半段存在少量能量，枝节内与直波导后半段几乎没有能量分布，因此只有少部分能量传输.

当开口方环谐振腔与带枝节直波导的距离G=90 nm保持不变，改变H从110 nm到170 nm，带枝节的直波导与开口方环谐振腔侧耦合波导的传输谱变化如下图6所示.

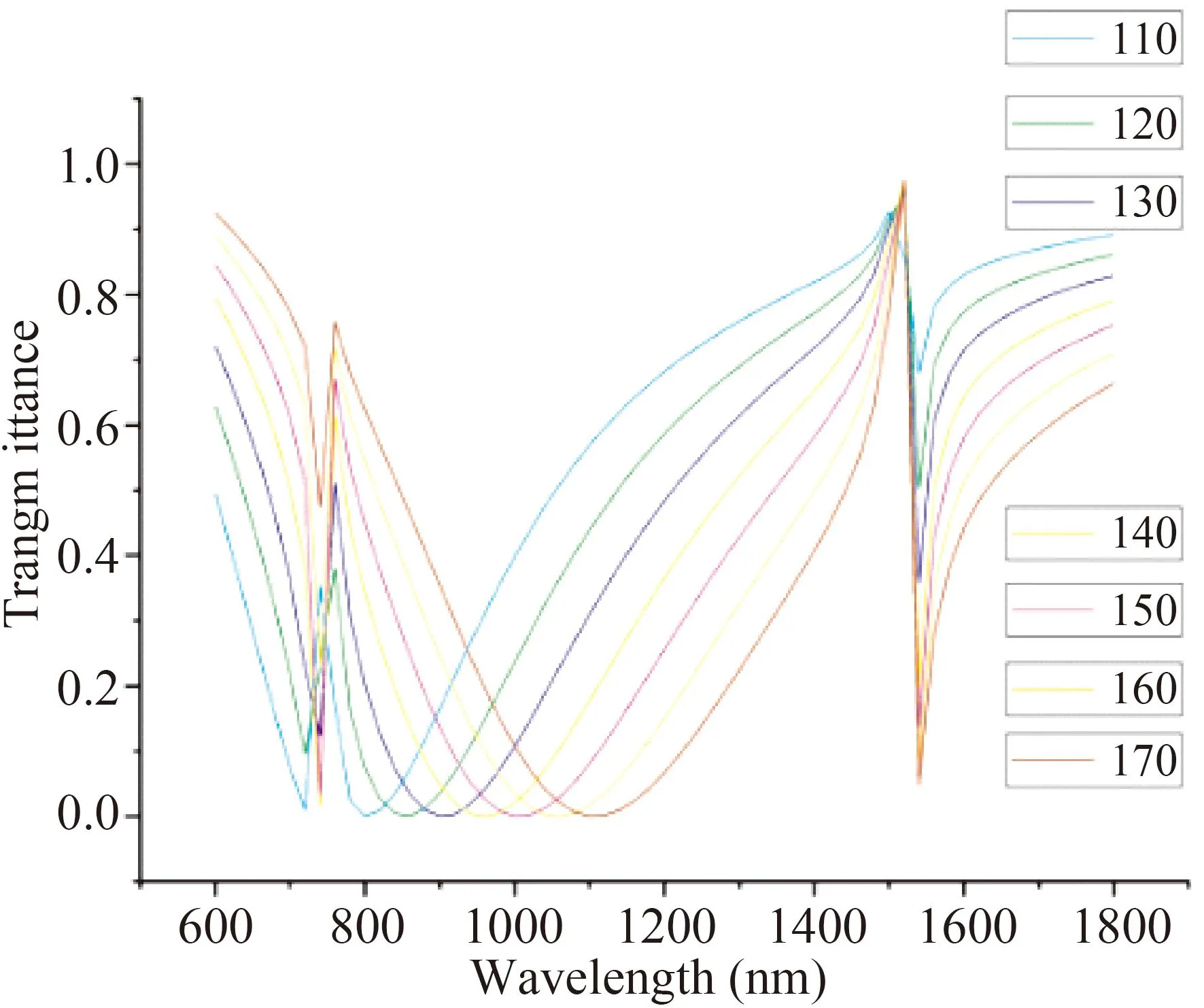
图6 随枝节高度 H的变化开口方环与带枝节的直波导谐振腔耦合传输谱Fig. 6 Coupled transmission spectra between open square ring and straight waveguide resonator with branches of different heights H.

图6表示开口方环与多个不同枝节高度的直波导谐振腔耦合的传输谱曲线，横坐标为波长，纵坐标为透射率. 图中的曲线所示当枝节高度由H=110 nm开始，每次增加10 nm，直到H=170 nm时的带枝节与开口方环谐振腔的直波导传输谱. 青色曲线为H=110 nm，绿色曲线为H=120 nm，蓝色曲线为H=130 nm，黄色曲线为H=140 nm，紫色曲线为H=150 nm，棕色曲线为H=160 nm，深棕色曲线为H=170 nm. 由图中可以看出，随着H增大，枝节传输谷的位置向长波长移动，这使得传输谱的左侧透明窗口变宽且不对称性增强，而右侧透明窗口基本上不随枝节高度H增大而变化.且左侧谐振随H的增大而增强，直至H=140 nm时左侧谐振达到最强，之后随着H的增大而减弱，甚至可能完全消失.

为了验证左侧谐振是否会完全消失，再次改变枝节高度，选取当枝节高度分别为H=200 nm和H=210 nm时，得到带枝节的直波导与开口方环谐振腔侧耦合波导的传输谱如下图7左边和右边所示.

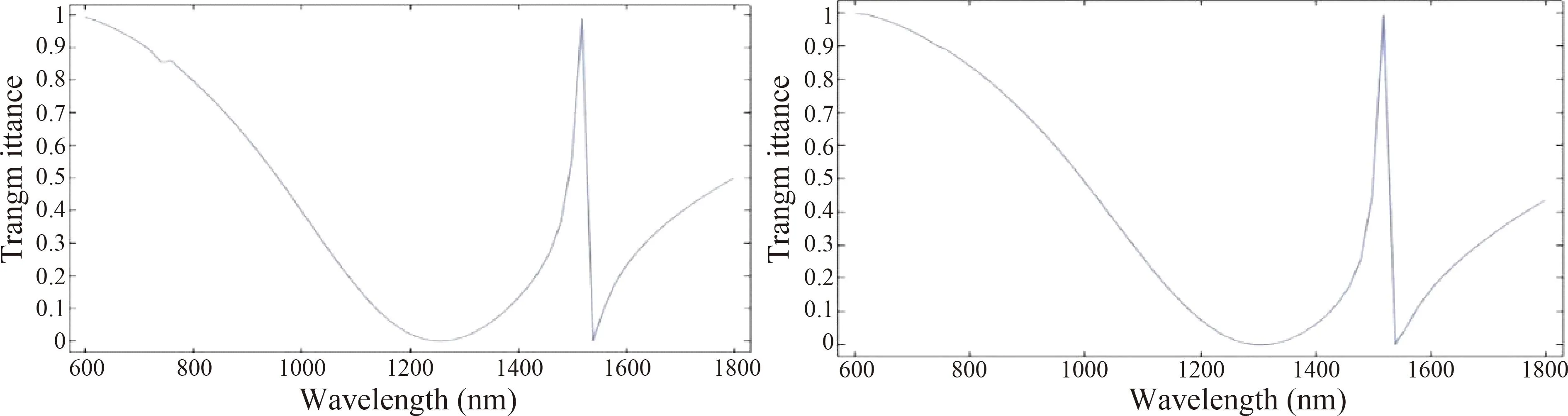
图7 开口方环与带枝节直波导谐振腔侧耦合传输谱(H=200 nm(左)H=210 nm(右))Fig.7 Side coupling transmission spectra of open square ring and straight waveguide resonator with branches (H=200 nm (left)H=210 nm (right))

由图7可以看出，当H=200 nm时左侧Fano谐振还存在，但已经十分微弱，当H=210 nm左边谐振完全消失. 而右侧Fano谐振与上面图形相比基本没有变化. 可以看出右侧Fano谐振不随H值而变化，具有很好的稳定性. 基于此，下面尝试将MIM结构的Fano谐振应用于折射率传感器领域.

3 带枝节的开口方环谐振腔传感器设计

折射率传感器需要有相对稳定的图像变化规律，因此带枝节的直波导与开口方环谐振腔是否可以应用于传感器领域还需进行检测，根据以上研究得到的信息该结构的传输谱中右侧的Fano谐振相对稳定，因此我们将右侧的Fano谐振作为主要的研究波段.

设置参数化扫描，因为仅观测Fano谐振的变化，所以将波长设置在1500 nm～1700 nm之间，同时改变介质折射率n，设定介质折射率n在(1～1.07)之间，基于有限元仿真得到不同介质折射率的传输谱如下图8所示.

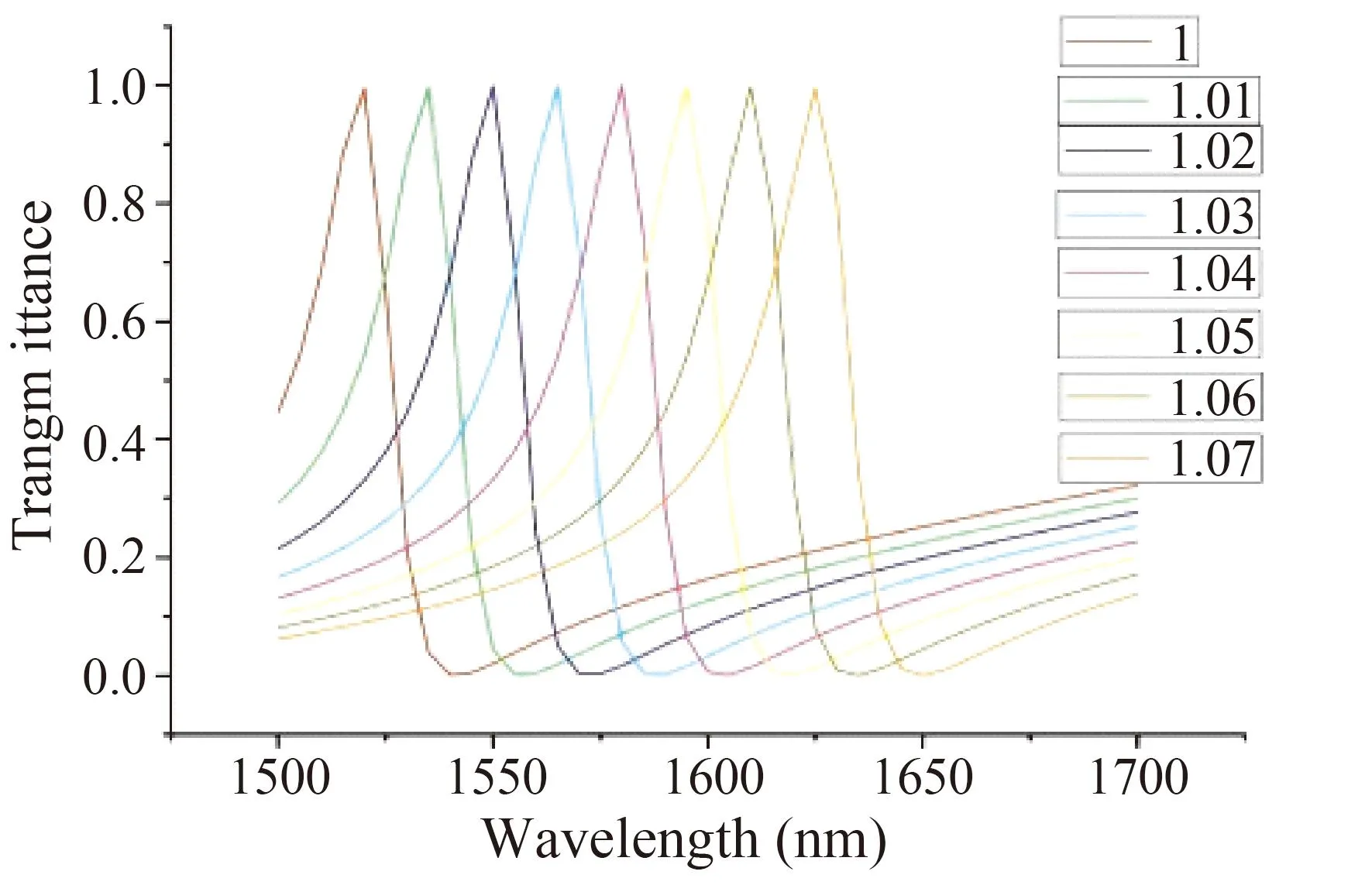
图8 带枝节的直波导与开口方环谐振腔侧耦合波导随介质折射率变化的传输谱Fig. 8 The propagation spectra of a straight waveguide with branches and a side-coupled waveguide with an open square ring resonator as a function of the refractive index

图8中横坐标为传输光波的波长，纵坐标为传输率. 图中可以看出各Fano谐振传输率曲线都呈现相同趋势变化，只是基于折射率变化下的曲线平移. 据此可以根据Fano谐振的位置大致确定填充介质的折射率，可以制作一个折射率传感器.

灵敏度S是衡量折射率传感器性能的重要指标，其表达式为[12]：

(2)

式中，Δλ为共振峰波长的偏移量，Δn为空气折射率的变化量．

品质因数(FOM)也是衡量传感器性能的重要指标，其表达式为[13]：

(3)

式中S为折射率传感器的灵敏度，FWHM 为共振峰的半峰全宽. FOM 数值越大，说明传感器的性能越好.

图9是开口方环与带枝节直波导谐振腔侧耦合波导Fano共振峰随折射率变化图，横坐标为折射率改变量，纵坐标为Fano共振透射峰改变量. 其中黑色方块为模拟得到的值，红色直线是拟合直线，可以看出Fano共振峰移动改变量与折射率变化量成非常好的线性关系，这为折射率传感器的应用提供了可能性. 该直线的斜率即为传感器的灵敏度S. 线性拟合可以得到该结构的灵敏度S为1496 nm/RIU，FOM=60.1.

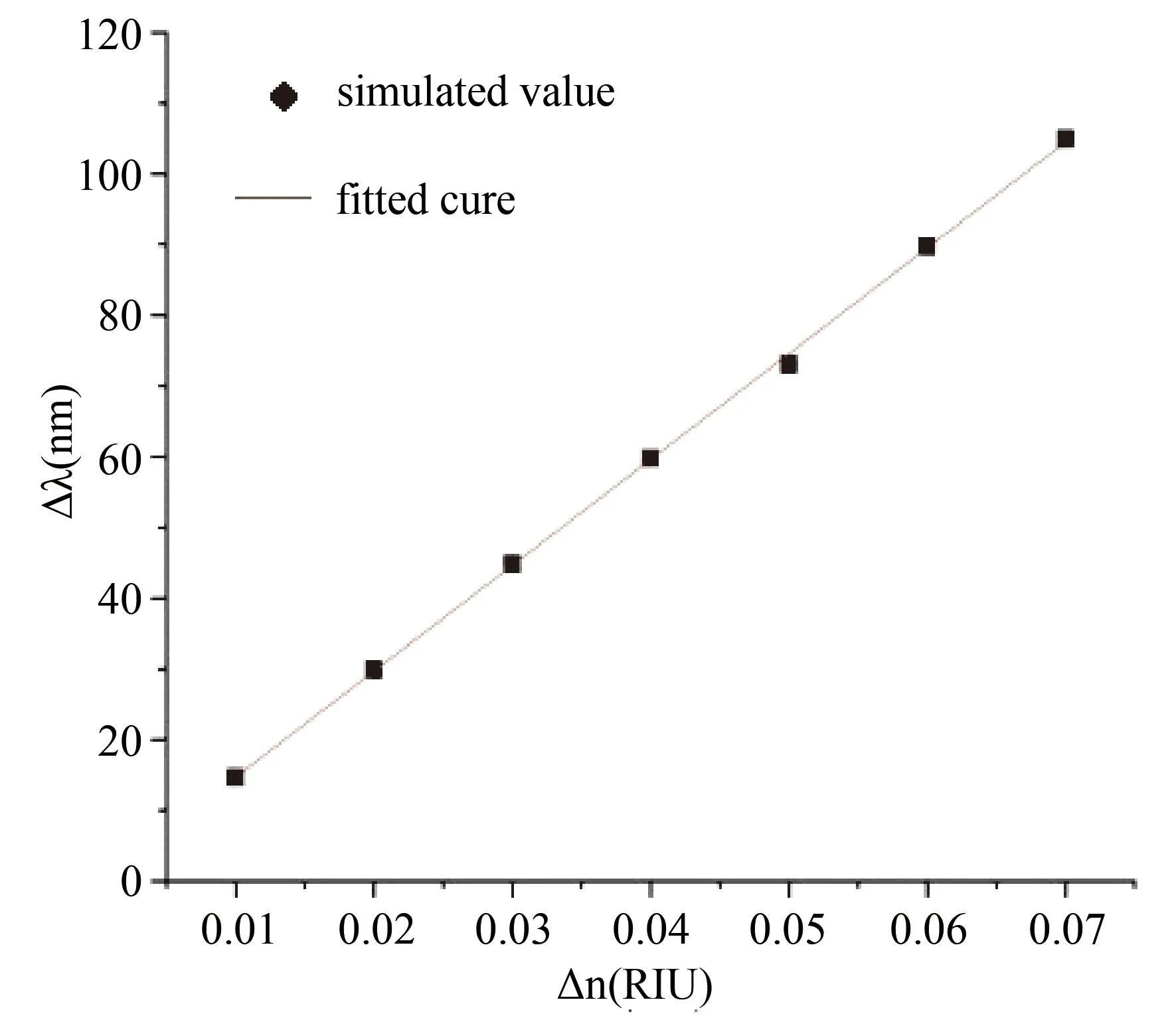
图9 开口方环与带枝节直波导谐振腔侧耦合波导Fano共振峰随折射率变化图Fig. 9 Variation of Fano formant of side-coupled waveguide with square ring and straight waveguide resonator with branches as a function of refractive index

4 结 论

本文基于MIM结构的Fano谐振原理，构建了带开口方环与有枝节直波导的谐振腔. 采用有限元法分析了该波导结构的透射谱线对结构参数的依赖关系. 结果表明：在波导与方环宽度w=50 nm，方环外边长l=350 nm，方环开口的长度B=90 nm，枝节高度H=140 nm时，开口方环与有枝节直波导的谐振腔结构中可以产生中心波长分别为λ=746 nm和1521 nm纵向及横向一阶谐振模式，两种谐振模耦合，将产生具有反对称线型的双重Fano共振透射峰. 进一步研究表明：其中左侧谐振峰值先随枝节高度增高而升高，至H=140 nm达到最大值，随后谐振峰值随枝节高度增高而缓慢减弱，直至消失. 而右侧谐振峰的高度几乎不受枝节高度H变化的影响. 受到枝节高度H影响最大的是传输谷. 随着枝节高度的增大，枝节谐振腔的传输谷向长波长的方向移动，而另两个传输谷基本保持不变. 当枝节高度为210 nm时，左边Fano谐振消失，只剩下右边的谐振，且谐振峰值基本保持不变. 设置参数化扫描，观测Fano谐振的变化，在波长1500 nm～1700 nm之间，设置最佳参数，经拟合计算得到该谐振耦合腔可以作为一个灵敏度S约为1496 nm/RIU，FOM=60.1的折射率传感器. 本文所设计的结构用作折射率传感器不仅具有很高的实际应用价值，还为设计新型亚波长纳米传感器提供了设计思路与理论参考. 该结构为片上集成的纳米级折射率传感器设计提供了有效依据.