凸近似避障及采样区优化的智能车辆轨迹规划

张宜旭，田国富，王海涛

沈阳工业大学 机械工程学院，沈阳 110870

自动驾驶是当前汽车开发技术的重点，而轨迹规划作为车辆系统的关键组成部分[1]，其理论方法最早出现在机器人领域[2]，智能汽车将其优化改进，以符合车辆模型并应对复杂交通环境下的行驶问题。自动驾驶中的路径规划分为两类：即基于高精地图下的全局路径规划和基于车辆周边环境变化的局部路径规划（轨迹规划）[3]，二者有许多相通的地方。

目前，常用的全局路径规划方法主要有基于采样的方法（随机采样、确定性采样等）、基于搜索的方法等。其中，Dijkstra 算法[4]与A*算法[5]为常用的经典搜索方法。如Bohren 等[6]采用Dijkstra 算法实现路径规划，但生成曲线不够平滑，需二次处理；王红卫等[7]根据A*方法进行改进，用以解决曲线转折频繁问题，但曲率不够连续。局部路径规划算法主要有人工势场法[8]、神经网络法等。如刘梓林[9]等基于人工势场法和点云数据进行道路规划，但效果受车辆尺寸影响较大。

快速拓展随机树（rapidly-exploring random trees，RRT）等采样方法为当前研究的热点，但缺点为生成的轨迹不连续[10]。为解决上述问题，冯来春等[11]通过限制RRT 采样区域来对结果进行优化；Jeon 等[12]基于RRT*算法，通过设计边界约束生成车辆轨迹。另外，利用多项式方法生成采样轨迹能够很好地解决该缺点，Werling等[13]基于Frenet坐标系通过采样和多项式拟合规划车辆行驶轨迹；张荣辉等[14]通过多项式方法生成多车换道轨迹簇。

为解决智能车辆避障轨迹规划时面临的采样区域划分问题，提出基于凸近似避障原理及采样区域优化的智能车辆轨迹规划方法：首先，引入凸近似避障原理[15-16]，通过本车与障碍物的位置及体积关系，得到轨迹可行域范围；对采样区域进行划分：将采样区域分为静态采样区、动态采样区、动态、静态障碍物采样区。采用“动态规划（DP）+二次规划（QP）”思想求解轨迹：首先利用多项式轨迹对采样点依次连接，建立动态规划代价函数并筛选得到粗略轨迹；构造二次规划的等式与不等式约束，对粗略轨迹进行平滑从而得到最优轨迹。

1 Frenet坐标系及转换关系

Frenet 坐标系以参考线（reference line）为基准，将车辆的平面运动解耦为纵向和横向的独立运动，并用(s,l)描述。其坐标系及参数如图1和文献[17]所示。

以(x0,y0)作为参考线起点，并将参考线均匀离散为一定数量的点，当点的数量足够密时，则纵向位移s近似为：

至此，完成了由直角坐标(xh,yh)向(s,l)坐标的转换。同理，可将道路环境中其他障碍物用同样方法进行转换[17]。

2 车辆轨迹规划算法模型

2.1 凸近似的局部避障原理

凸近似避障原理实际是由多个凸多边形构成的车辆安全行驶区域。对自车和障碍车做如下定义：

（1）令自车质心位置为p0=[x0,y0]T，另外设置向量dk∈R2，k=1,2,…,r。由于车辆为矩形，因此可将自车包含在多边形p0+conv{d1,d2,…,dr} 中。显然，当dr=0 时，则自车将简化为一个点。

（2）令障碍车的参考点表示为qi∈R2，i=1,2,…,M。其中，M为障碍物数量。设p0,q1,q2,…,qM∈R2，p0≠qi，i=1,2,…,M，故可以得到凸多边形区域P：

式中：

当i=1,2,…,M时，p0存在于凸多边形p中，qi不在凸多边形p中，最终形成如图2 所示的车辆行驶安全区域。

在实际行车过程中需要考虑障碍车外形尺寸，因此，车辆安全行驶空间应较凸空间相对减小。如图3所示。

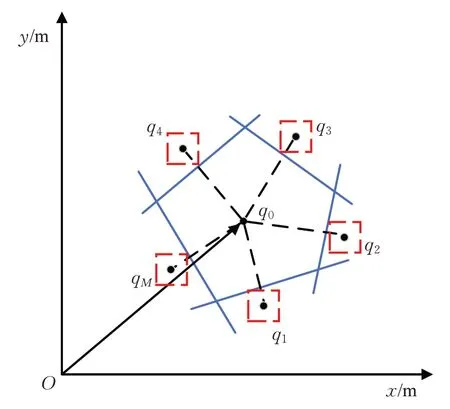
图3 去除障碍物的凸空间示意图Fig.3 Schematic diagram of convex space for removing obstacles

凸近似避障原理通过本车与障碍车的质心距离及方向，构建出车辆安全行驶区域。以车辆避障为例，其安全行驶区域如图4所示。

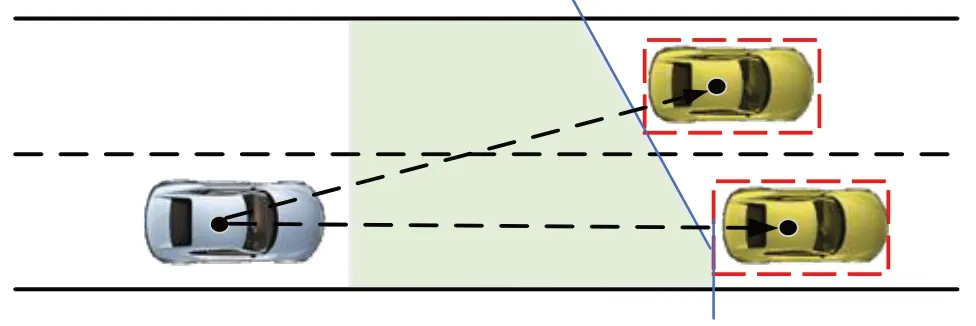
图4 避障可行域示意图Fig.4 Schematic diagram of obstacle avoidance feasible domain

本车通过雷达与传感器，测得两者质心之间的方向与距离。考虑到障碍车的外形尺寸，故其所占据的区域皆为危险区域（图4中红色框所示）。另外，车辆通过高精度地图获取道路边界，进一步限制该可行域范围，最终其可行凸空间如图4灰色区域所示。

另外，可对障碍物外形所占据的区域设置一个膨胀系数q，进一步保证其行驶安全性。同理，对于多障碍物，应用此方法同样可得到可行域。

2.2 问题建模

一般而言，车辆的行驶轨迹可以近似看成一系列离散点，因此，轨迹规划可以看作离散点(x,y)的规划，速度规划可以看作到达每个离散点的时间。因此，轨迹规划可以看作在三维空间(x,y,t)内找到在约束下的最优离散点。如下式：

式中，z为优化目标，即轨迹点序列，有p个不等式约束和q个等式约束。

为保证车辆行驶安全性和应对突发状况，轨迹规划应满足实时性要求，因此可设置算法以合适的频率执行。为了减小问题运算规模，优化算法运行时间，可使用交替优化[18]思路将原本(s,l,t)三个维度的优化问题转换为两个二维的S-L 与S-T 优化问题，分别对应轨迹规划与速度规划。

另外，轨迹规划与跟踪算法应考虑合适的车辆运动学或动力学模型，使轨迹完全符合车辆实际运行情况，因此可采用文献[19]所展示的简化后的车辆模型。

3 车辆采样区设计

3.1 采样区定义

在Frenet 坐标系下对空间进行离散采样的区域称为采样区。按照文献[20]，当本车探测到前方障碍物并相距一定距离后，本车开始采样，其采样区始终为距车辆前方一定长度S的整个路面区域。如图5所示。

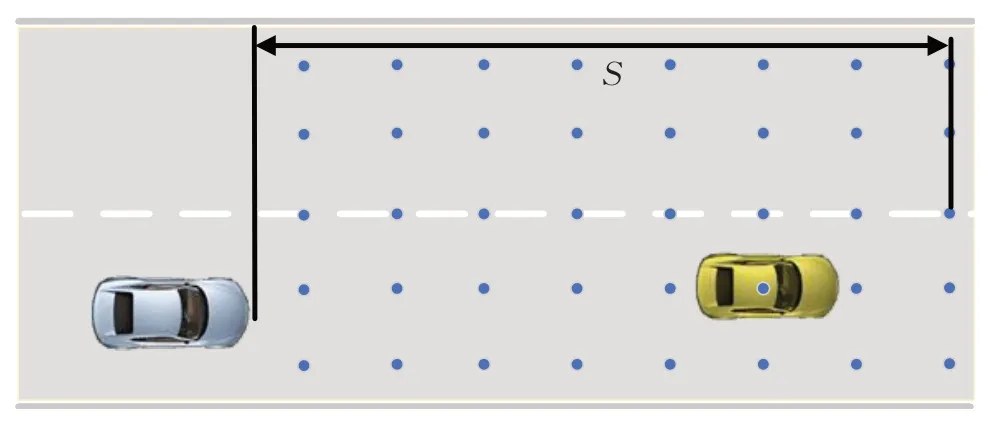
图5 传统采样区Fig.5 Conventional sampling area

由于车辆在行驶过程中，尤其是在高速情况下，其横向变化量应保持在较小范围内以维持车辆行驶稳定性。并且，当相距前方障碍物较远距离时，本车不需要过大的横向位移去进行避障。因此，在图5所示的传统采样区的基础上，可将纵向上距本车较近且横向上距本车较远的采样点舍去，为保证避障的安全性，同时稍微增加其采样距离S。而当本车逐渐逼近障碍物时，采样点数应逐渐增密，从而保证最优避障轨迹。

根据采样点数的变化情况，可将采样区划分为动态采样区与静态采样区两部分。并且在障碍物附近设置障碍物采样区，且始终包含在静态采样区内。

以车辆左换道为例，其采样区划分如图6所示。

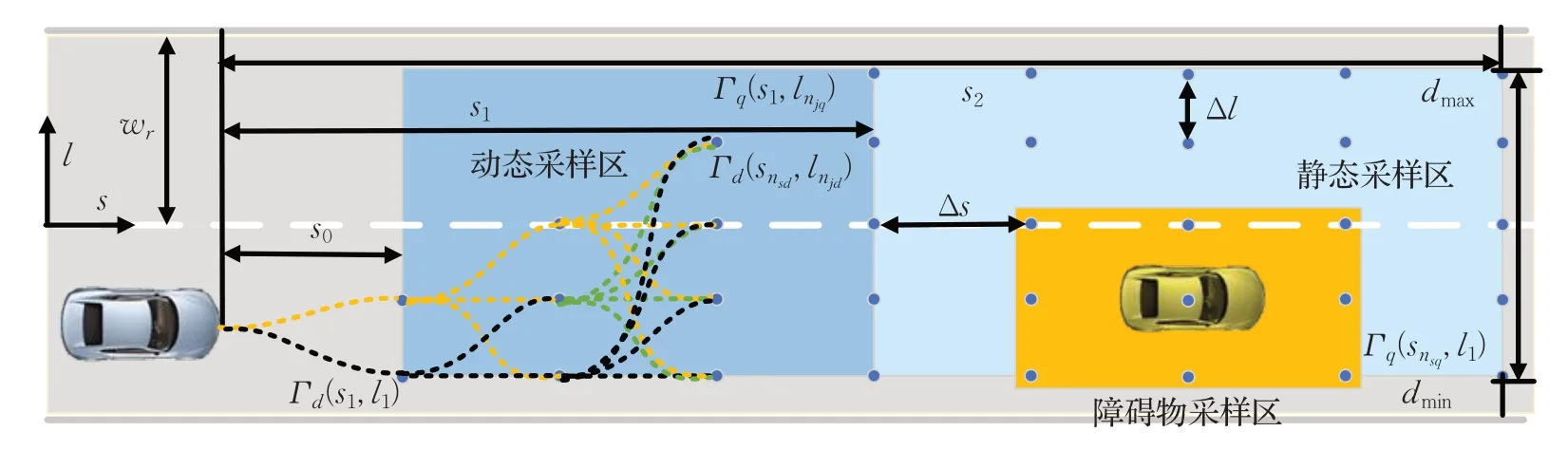
图6 采样区定义Fig.6 Sampling area definition

式中，nsd、njd表示动态采样区内的纵向、横向采样点个数，nsq、njq表示静态采样区内的纵向、横向采样点个数。s0、s1、s2表示采样区边界距本车车头之间的距离。以道路中心线为零位置，dmax、dmin分别表示采样宽度的两侧边界。

为确保车辆不会超出道路边界，则：

式中，wr为车道线宽度，w为自车车宽。

等间隔的离散点表示为：

式中，s(k+1)、l(k+1)分别表示在第k+1 点的s、l坐标，s(k)、l(k)分别表示在第k点的s、l坐标，Δs与Δl分别为相邻采样点的纵向间隔与横向间隔。

3.2 动态采样区与静态采样区

动、静态采样区逐渐过渡过程如图7所示。

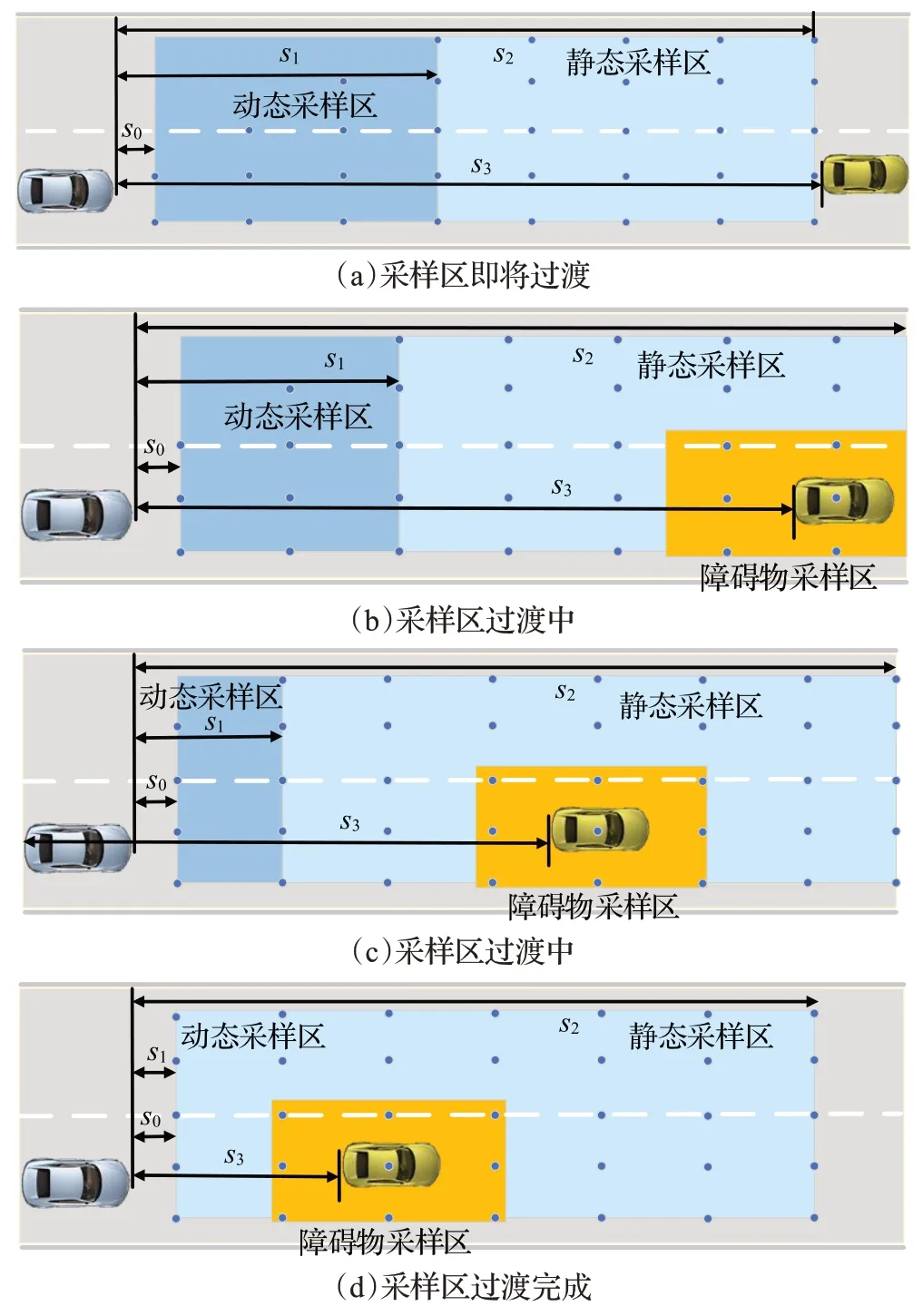
图7 采样区过渡Fig.7 Sampling area transition

图7（a）为本车采样初始阶段，由于障碍物并未进入采样区内，即障碍物距离s3大于采样区长度s2，本车并不需要进行避障求解，此时动态采样区与动态采样区未产生过渡，故此时动态采样区面积最大。采样区长度s2由采样点纵向间隔Δs及采样点总列数nL决定，根据3.1节，有：

式中，s0为本车车头距第一列采样点的纵向距离，采样点总列数nL=nsd+nsq。

根据图7，采样区内采样点的最大行数nH为：

另外，由于动态采样区内采样点数量随着本车距障碍物的距离的降低而逐渐增加，因此，可设置动态采样区内相邻两列的采样点的个数相差1，如图7所示，故动态采样区采样点随障碍物的接近逐渐增加一行可形成对静态采样区的过渡。

根据图7（a），此时动态采样区其右边界s1为：

应将障碍物始终包含在静态采样区内，该区域内采样点数足够多，以保证可求得最优解。有：

式中，δ1、δ2为纵向间隔系数，用以保证障碍物与静态采样区左边界的距离大小。二者相差越大，则距离越大。

根据图7 与式（11），随着障碍物的逼近，两采样区间进行过渡，采样点数量逐渐增多，直至s1=s0时，采样点数量达到最大。

3.3 障碍物采样区

为简化运算，可在障碍物附近设置障碍物采样区，根据距离代价函数，将区域内满足代价大小的采样点选择性忽略。

一般而言，道路障碍物分为静态、动态障碍物两种，应根据不同情况分别设置障碍物采样区。

3.3.1 静态障碍物采样区

在自然坐标系下，若障碍物速度vobs满足：

可将其视为静态障碍物。式中vmax为动、静态障碍物的速度边界。另外，设置障碍物距离代价函数：

式中，k为距离代价常数，d1、d2为距离常数，xiq,jq为静态采样区内采样点Γq(siq,ljq)对障碍物质心(s0,l0)的距离，对采样点做遍历：

3.3.2 动态障碍物采样区

相对于静态障碍物，动态障碍物与本车的两次相遇（本车头部与障碍物尾部、本车尾部与障碍物头部）之间的行驶范围皆为危险区域，因此可将该区域作为静态障碍物进行处理：

首先对动态障碍物进行筛选：

式中，vs为本车车速。当满足上述情况时，本车与障碍物距离逐渐降低。在该过程中，动态采样区与静态采样区进行正常过渡，其动态障碍物采样区按照3.3.1 节的方法进行计算，使得障碍物质心始终包围在应舍去的采样点区域内，正如图7 所示。由于障碍物向前运动，因此障碍物采样点随障碍物质心进行更新。

当本车与障碍物的距离代价满足一定条件时，本车执行换道操作。此刻二者关系如图8（a）所示。

图8 超车过程Fig.8 Overtaking process

图8（a）中黑色采样点为按照3.3.1小节的方法计算出的障碍物采样点。另外，在未来采样时刻，由于障碍物向前运动，障碍物采样区内采样点个数应在此基础上随着障碍物运动方向逐渐增加，直至本车二次换道绕过障碍物。

图8（a）中障碍物采样点位置及相对于障碍物质心(s0,l0)代价已知，本车对其记录。设置算法计算频率为fM，则每隔秒，本车对采样区进行重新遍历计算。

由于障碍物的运动，障碍物质心坐标由上一个采样时刻的(s0,l0)变为(s1,l1)（正如图8（a）（b）所示），此时根据采样点与障碍物质心坐标间的距离代价，其障碍物采样区域在障碍物前进方向递增一列（正如图8（b）中绿色采样点），此时上一时刻所记录的障碍物采样点（图8（b）中黑色采样点）代价以及当前时刻所递增的采样点代价在当前时刻得到更新，对于某个重复的采样点，其代价有：

为保证本车在相邻车道的行驶安全以及在第二次换道过程中避免被障碍物追及，可在障碍物前方设置长度为L的障碍物区域，将该区域内所包括的采样点作为障碍物采样点，如图8（c）中橘黄色采样点所示，有：

其中，n=1,2,…,n。其n值受障碍物速度影响，若障碍物速度越高，为保证足够安全，n取值越大，障碍物前方采样点越多。由图8（c）所示，n=1。

其每列的采样点个数以障碍物中心为参考，对称分布。有：

式中，w为障碍物宽度，n1为每列障碍物采样点个数，应取满足上式的最小整数。如图8（c）所示，其值为3。

至此，动态障碍物与本车的两次相遇过程之间障碍物行驶区域，以及障碍物前方长度为L的区域已作静态障碍物处理，利用上节对静态障碍物的处理办法，将此类采样点从整体中剔除，为下文实现对动态障碍物的避障提供条件。

4 车辆轨迹规划

采用“动态规划+二次规划”的思想。首先根据Δs与Δl确定采样点的分布并利用多项式轨迹进行连接，通过构建动态规划目标函数对轨迹进行筛选，从而得到粗糙换道轨迹。之后利用二次规划理论对粗糙轨迹进行平滑，从而得到符合车辆运动特性的换道轨迹。

4.1 基于五次多项式的车辆运动轨迹

首先，应需要选择合适的多项式轨迹对采样点进行连接。在Frenet坐标系下，车辆轨迹信息为：

其中，自变量为纵向位移s，因变量为横向位移l。设车辆准备换道时刻其质心为(s0,l0)，根据坐标系转换原理及车辆传感器，有：

式中，θ为车辆航向角。假设在换道时刻，本车与采样点的关系如图9所示。

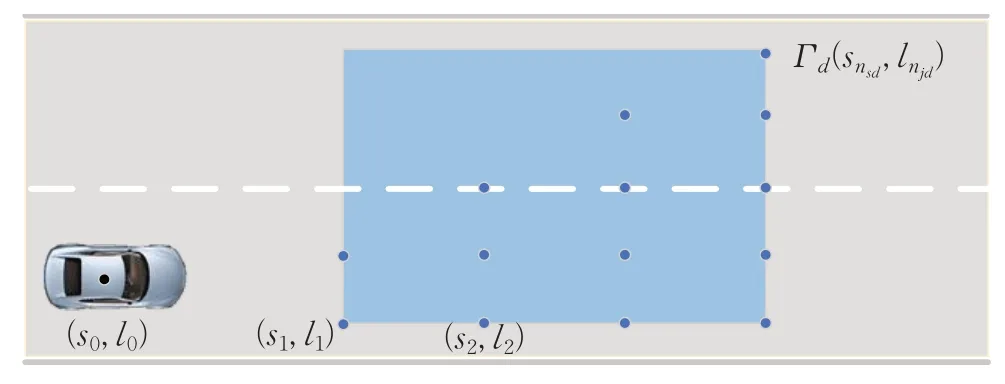
图9 本车及其采样点Fig.9 This vehicle and sampling points

为保证车辆行驶稳定性，则本车在相距最近的采样点处的侧向速度与加速度应为零，则位姿信息为：

同理，根据图9，在另外采样点的位姿信息有：

以此类推，可得到每个采样点处的位姿信息。因此，若对相邻两列中的两个采样点做平滑轨迹连接时，其轨迹信息应满足如上6个条件。因此应选择5次多项式轨迹，其未知项系数的个数为6，其一般形式为：

按照此方法，将相邻两列的采样点进行遍历，形成如图6所示的轨迹束。

4.2 车辆轨迹的动态规划

当规划出轨迹束之后，应从中筛选出一条最优轨迹，因此，可通过设立合适的动态规划目标函数实现。

（1）轨迹应保持平滑，防止车辆跟踪时发生抖动，因此其轨迹平滑代价如下：

（2）本车应尽量在车道中心行驶，防止相邻车道的其他车辆对本车的影响。因此，设置参考线距离代价：

式中，w4为偏移权重系数，li为轨迹的横向位移，lref为道路中心线的横向位移，一般作为参考线，其值为0。

因此，两者代价之和可作为动态规划目标函数：

由于轨迹连接相邻两列的采样点，且采样点为多列，故轨迹为分段短轨迹，如图10所示。应采用合适方法对其进行连接，组成一条能够避障且代价函数最小的长轨迹。

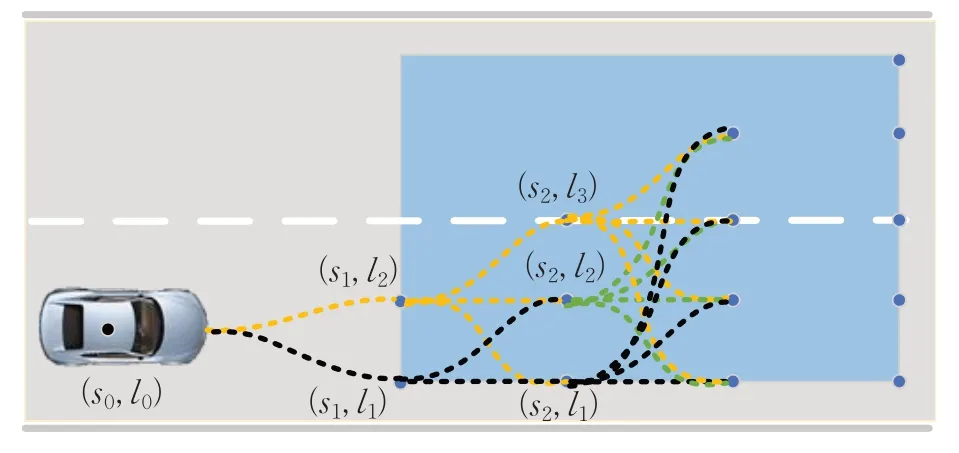
图10 分段短轨迹示意图Fig.10 Schematic diagram of piecewise short trajectory

首先，对于其某个终点采样点（如图10中的(s2,l3)），从(s0,l0)出发，其轨迹连接方式有：

最终，对轨迹束进行遍历筛选，选取其小值进行短轨迹拼接，从而得到最优长轨迹。如图11所示。

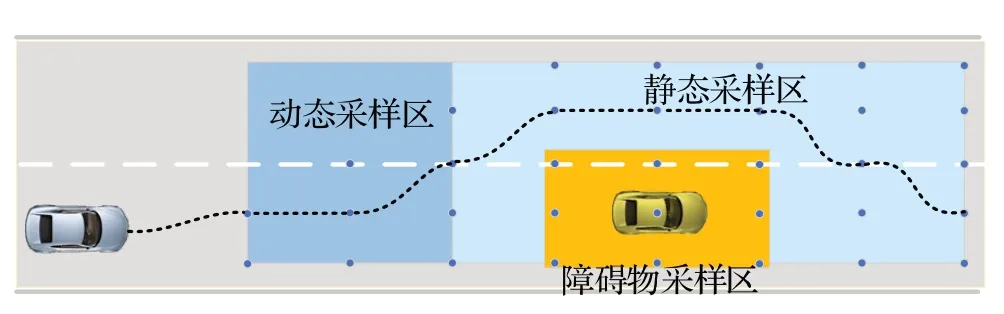
图11 最优长轨迹Fig.11 Optimal length trajectory

4.3 车辆轨迹的二次规划

4.3.1 二次规划目标函数构造

当动态规划筛选出粗略轨迹之后，可利用二次规划进行平滑。

二次规划（QP）是应用非常广泛的非线性规划问题。其标准形式定义为：

式中，X为待求解变量；H为Hessian 矩阵；f为梯度向量。若H矩阵为半正定或正定，则该问题称为凸二次规划问题。

首先设置合适的目标函数以求得最优轨迹，目标函数由如下三部分组成：

（1）平滑性

（2）靠近道路中心线

与式（25）类似，本车应尽量在车道中心行驶，故轨迹应靠近道路中心。式中lmax、lmin分别为道路上下边界，li为轨迹横向位移，wmid为权重。

（3）轨迹终点状态约束

至此，二次规划目标函数为：

对该式进行标准化转换。设二次规划优化变量为：

梯度向量f为：

至此，将目标函数转换为如式（29）所示的标准形式。

4.3.2 二次规划约束条件的构造

转换成矩阵形式，有：

优化变量为式（34）所示，根据式（38），有：

至此，完成目标函数的等式约束条件。

另外，在规划出粗略凸空间之后，由于车辆有形状与体积，因此每个边界点碰撞情况都不同，如图12所示。

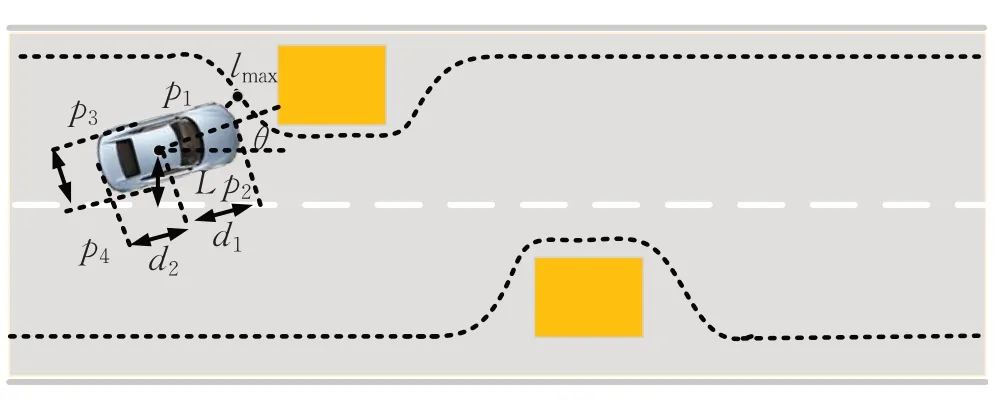
图12 车辆碰撞情况图Fig.12 Vehicle collision diagram

图12中，p1、p2、p3、p4为车辆四个边角点；d1、d2为质心距车头、车尾之间的距离；L为质心距参考轨迹的横向距离；w为车辆宽度；θ为车辆行驶方向与参考轨迹的夹角。此时：

式中，lp1、lp2、lp3、lp4为车辆边角点距参考轨迹的纵向距离，将上式进行简化，令sinθ≈tanθ≈l′，cosθ≈1。

另外，如图12 所示，当车辆接近左前方障碍物时，p1边角点会首先碰撞，此时p1点与距该点横向的障碍物边界距离lmax为零。为保证车辆行驶安全，应：

同理，当车辆靠近右前方障碍物时，有：

综合可得：

优化变量为式（34）所示，根据式（43）可得：

式中，A=O8n×3n;b=O8n×1;其中A(8i-7:8i;3i-2:3i)=As；b(8i-7:8i;1)=bs；i=2,3,…,n。至此，完成目标函数的不等式约束条件。

综上，通过matlab 中的quadprog 求解器，通过以上约束条件，结合车辆的纵向位移s，可计算出一条可供车辆行驶的最优轨迹。如图13所示。

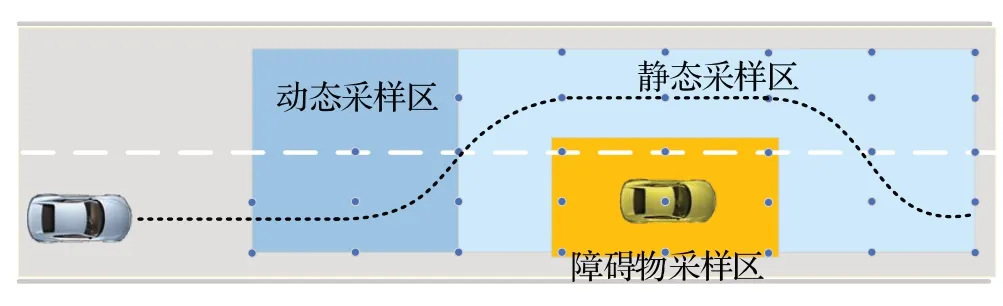
图13 车辆二次规划最优轨迹Fig.13 Optimal trajectory of vehicle quadratic programming

对比图13与图11，通过二次规划之后，其轨迹较为平滑，符合车辆跟踪条件。另外，平滑程度与目标函数内的权重系数有关，若权重系数越高，则轨迹越平滑，但求解速度会变慢。因此，应合理选取其权重系数。最后，求解出的最优轨迹通过坐标系转换原理转换至全局坐标系下供车辆跟踪，实现车辆的避障。

5 多场景仿真验证

为验证本方法的有效性，可通过搭建Prescan-Carsim-Matlab/Simulink联合仿真平台进行验证。其中：Prescan用来构建道路行驶环境，设置汽车、行人等障碍物变化；Carsim 用来设置车辆本身配置等系统参数；Matlab/Simulink用来搭建系统算法。

为更直观地观察方法的优劣，搭建与文献[17]参数相同的方法做对比，在相同场景下观察二者避障轨迹规划效果。本方法仿真参数如表1所示。

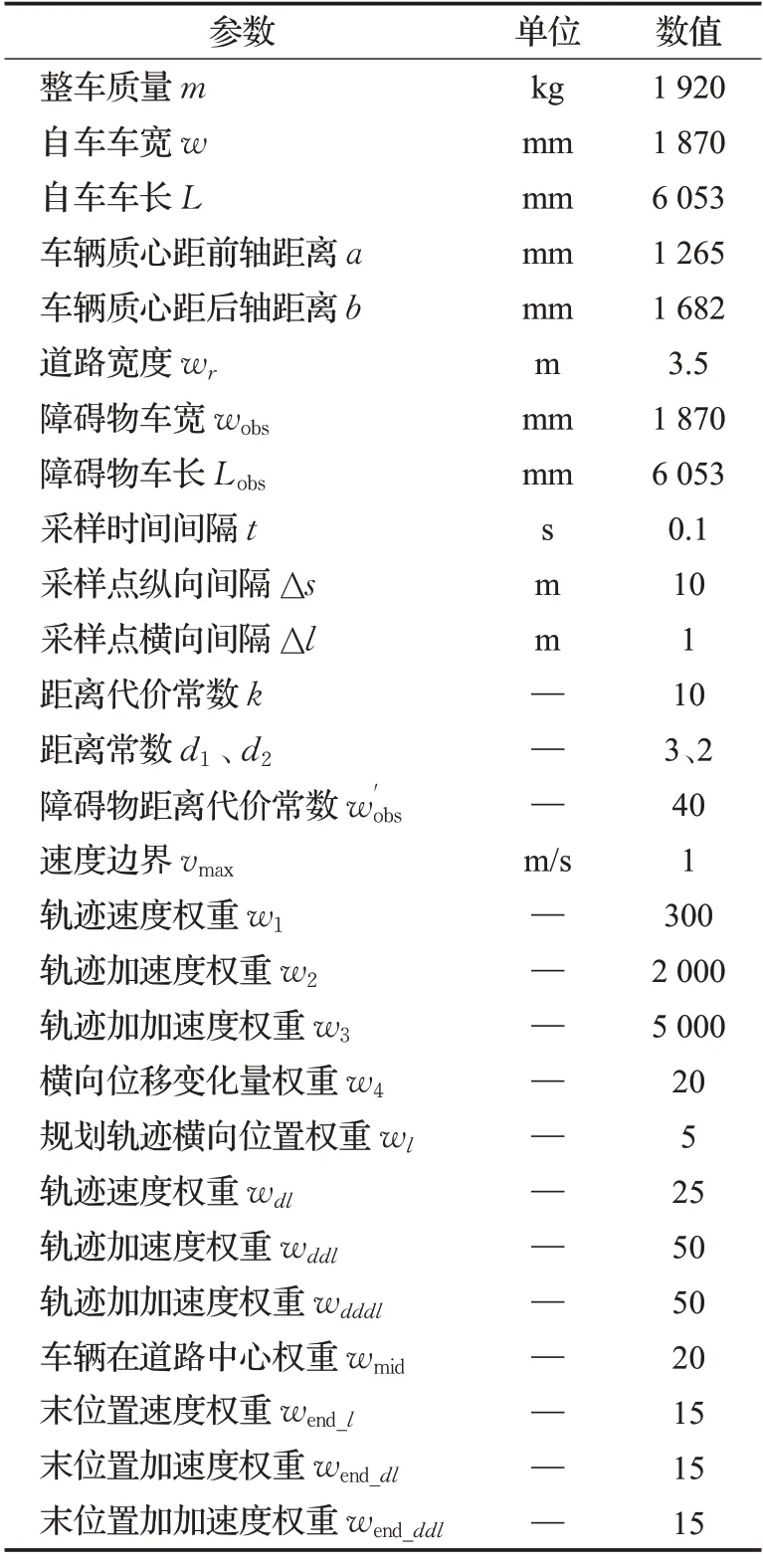
表1 仿真参数Table 1 Simulation parameters

本文采用同向笔直双车道仿真场景，该道路通过道路边界及中心线三组离散点拟合而成。设计三种场景对本车进行验证：即本车分别对静态障碍物、低速障碍物、动态障碍物这三种场景的避障操作。

5.1 静态障碍物仿真验证

智能车通过该场景时的轨迹如图14 所示，其中蓝色线表示自车按本文方法在当前时刻所规划的最优轨迹，绿色线为文献[17]的方法所规划的最优轨迹。

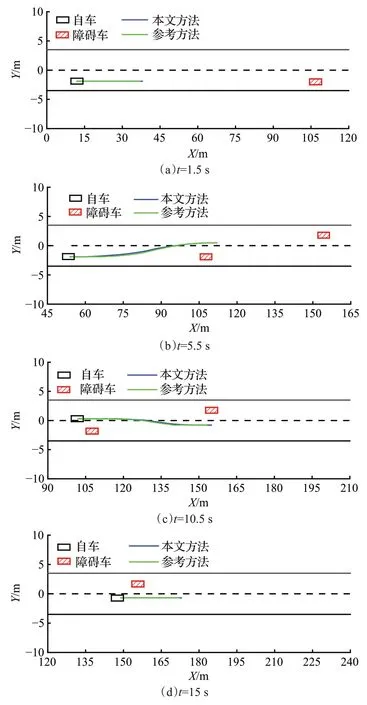
图14 静态障碍物避障过程Fig.14 Static obstacle avoidance process

设定本车行驶速度始终为10 m/s，从t=0 s 仿真开始阶段，自车向正前方运动；在t=1.5 s 时，车辆前方障碍物由于距离较远，未对本车轨迹产生影响；在t=5.5 s时，车辆已探测到前方障碍物，这两种方法皆只规划出对车辆最近的障碍物的避障轨迹；在t=10.5 s 时，在越过第一个障碍物之后，接着对下一个障碍物进行避障轨迹规划；在t=15 s时，车辆继续前行，避障完成。由图14可知，此两种方法所规划出的轨迹相差不大。

5.2 低速障碍物仿真验证

设定障碍车车速为0.9 m/s，对于本文方法而言，由于其速度不高，可按照静态障碍物处理。参考方法未牵扯到对动态障碍物的避障操作，但可通过提高其碰撞损失权重，从而增加规划的轨迹对障碍物的距离以保证其安全性。其避障过程如图15所示。

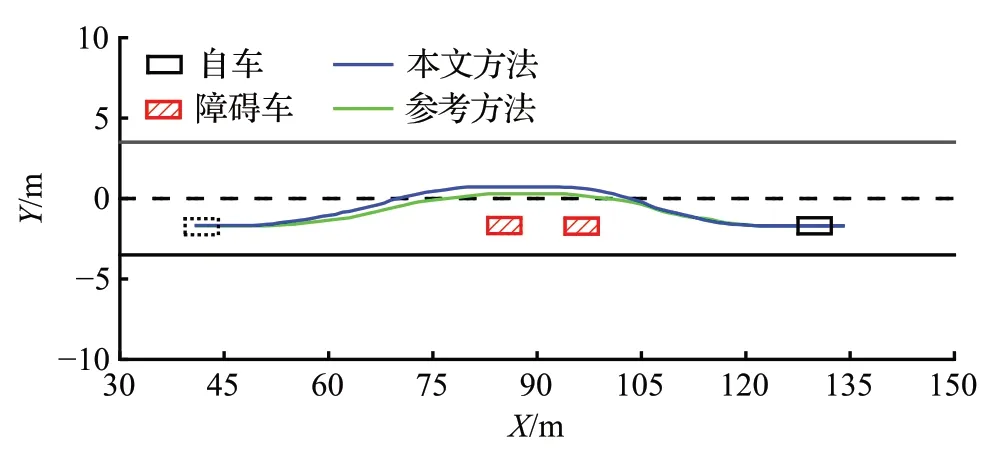
图15 低速障碍物避障过程Fig.15 Low speed obstacle avoidance process

黑色、红色虚线矩形框表示分别表示本车与障碍车开始避障时刻的位置，当换道结束时刻，障碍物位置由红色矩形框所示，本车位置由最右方黑色矩形框所示。

由图15 可知，两种方法在两次换道阶段轨迹相差不大，但本文方法在相邻车道上距障碍物的纵向距离比参考方法较远，其安全性更高。而对于参考方法来说，合适的碰撞损失权重能提高其碰撞安全性。

5.3 动态障碍物仿真验证

（1）障碍物做匀速运动

设定障碍车匀速运动的车速为6 m/s，由于其速度高，故本方法应按照动态障碍物处理，另外，参考方法应选择合适的碰撞损失权重对其进行避障。该过程如图16所示。

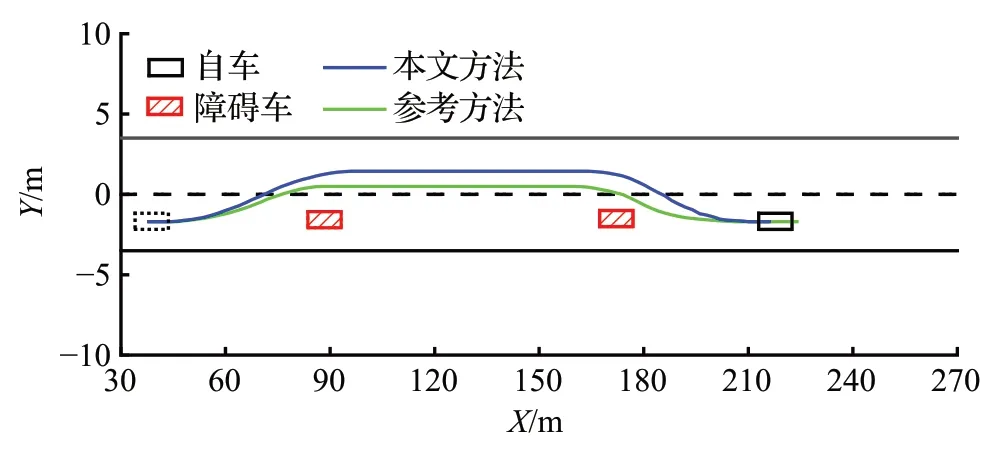
图16 匀速障碍物避障过程Fig.16 Constant speed obstacle avoidance process

（2）障碍物变速运动运动

设定障碍物前10 s 做速度为6 m/s 的匀速运动，之后保持静止。其避障过程如图17（a）。

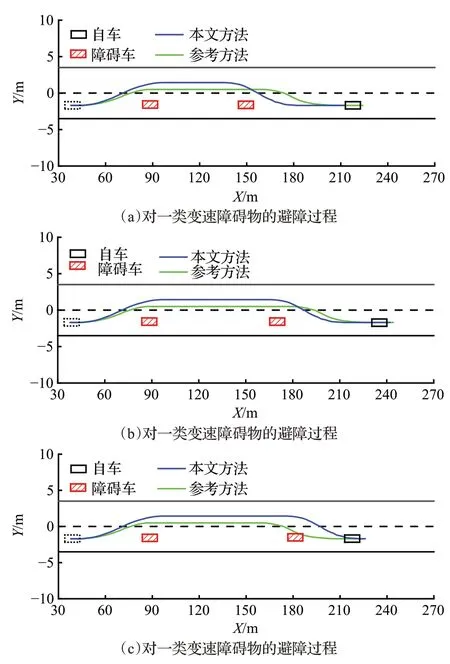
图17 变速障碍物避障过程Fig.17 Variable speed obstacle avoidance process

设定障碍物前10 s 做速度为6 m/s 的匀速运动，之后以1 m/s2的加速度做匀减速运动。其避障过程如图17（b）。

设定障碍物前10 s 做速度为5 m/s 的匀速运动，之后以1 m/s2的加速度做匀加速运动。其避障过程如图17（c）。

对于匀速障碍物而言，由图16所示，两种方法皆能避过障碍物，但参考方法与障碍物距离较低，不能保证换道安全性。

对于变速运动障碍物，由图17（a）所示，本文方法参考方法未能及时处理先运动后静止的障碍物，因此在二次换道时刻，参考方法距障碍物距离过远，不利于车辆通行效率，另外，在相邻车道行驶过程中，距离障碍物过近。

对于先匀速后减速的障碍物如图17（b）所示，与图17（a）类似，参考方法在二次换道段距障碍物稍远，在相邻车道段距障碍物过近。

对于先匀速后加速的障碍物，如图17（c）所示，参考方法在二次换道段与障碍物相撞，且在相邻车道行驶段距障碍物过近。

综上，对于静态障碍物而言，二者效果相差不大。对于动态障碍物的避障，本文方法优于参考方法。

6 结论

针对结构化道路下做匀速运动的智能车辆避障轨迹规划问题，以及基于采样的轨迹规划方法未将采样环境做区域划分问题，提出基于凸近似避障原理及采样区域优化的智能车辆轨迹规划方法，并与文献[17]方法进行对比。仿真结果表明，该方法能够有效地得到平滑轨迹并避开障碍物。