基于多孔特征约束的舱段对接姿态识别方法*

谭宏泽，李志杰，季 薇，于 博，王怀明

（1.北华航天工业学院，廊坊 065000；2.燕京理工学院，廊坊 065201）

随着大型机械产品装配技术开始数字化、智能化发展，位姿测量技术成为大型产品对接系统的关键技术，取代传统的人工对接方式是必然的趋势[1]。视觉测量系统设备搭建方便、相机价格合理以及计算机性能提高，因此，基于视觉的位姿测量方法在大型舱段装配中被广泛运用[2]。由于舱段的尺寸大以及相机的视场局限性，舱段对接阶段通常借助靶标等辅助工具作为舱段位姿的测量特征点[3]，但靶标在安装时存在定位误差。对于飞机、航天器等大型舱段以及端面上的孔和销的协调准确度和轴线有严格精度要求[4]，因此，目前大型部件装配会选择部件上的装配孔作为关键特征，通过多个装配孔来拟合出大型部件的空间位姿或直接利用装配孔的位姿实现大型部件的装配。

目前，最广泛的舱段对接方式是点集匹配，利用舱段上的对接孔和对接销的位置关系来解算出拟合舱段的位置矢量，但很多情况下只考虑了孔和销的圆心位置约束，而忽略了孔和销的姿态方向约束，这会导致在对接中两舱段轴向匹配存在较大偏差。

针对大型舱段姿态估计以及舱段对接的问题，国内外有不少研究。哈尔滨工业大学的宋兴君[5]借助跟踪靶标来估计舱段的姿态，以及利用测量转换光笔来测量对接销和对接孔的姿态；西安电子科技大学的徐康力[6]利用舱段端面的局部销孔对接来完成两个舱段的相对转角测量，通过舱段上局部的销孔匹配实现舱段的匹配；陈栋等[7]通过激光跟踪仪测量舱段上的关键特征投影点的空间坐标，构建舱段端面方程，解算端面法向量为舱段端面的姿态方向；何晓煦等[8]提出了基于LM迭代的最小二乘法对飞机大部件位姿估计，利用飞机大部件上的几个点来拟合部件的整体姿态；王青等[9]提出了基于对接孔协调准确度的飞机大部件位姿优化算法，其中建立了装配姿态评价的最优化数学模型，使得孔轴方向的误差最小；秦宇等[10]提出了几何分析法和小旋量模型来求解姿态。

在大型舱段制造过程中存在舱段端面上的装配孔制造误差，也会使装配孔的空间姿态与舱段整体姿态不一致，即装配孔的轴向和舱段轴向存在偏差。因此，当舱段端面的装配孔系中每个孔的姿态均不同时，若装配孔逐个匹配并调整姿态，很难保证舱段对接精度。因此，能拟合出舱段的最佳姿态可提高舱段对接的精度。本文提出了多孔约束的舱段整体姿态估计方法，首先通过双目视觉系统获取装配孔的姿态，之后建立姿态优化模型，该模型是求一个投影向量，使得若干个装配孔的姿态矢量投影在该投影向量上的模和最大，采用遗传算法（Genetic algorithm，GA）对模型求解，从而实现舱段整体姿态方向估计。

1 装配孔姿态分析

大型舱段在装配过程中需要考虑舱体上定位孔销、螺栓孔销等装配孔销的对接协调问题，其中包括位置匹配、孔轴线对合等问题，因此会出现以下4种对接情况：（1）舱段端面上装配孔销的位置匹配和装配孔销轴线对合均存在较大偏差； （2）舱段端面上装配孔销的位置匹配偏差满足精度需求，但装配孔销轴线对合存在较大偏差； （3）舱段端面上装配孔销的位置匹配存在较大偏差，但装配孔销轴线对合偏差满足精度需求； （4）舱段端面上装配孔销的位置匹配和装配孔销的轴线对合偏差满足精度需求。

在第4种情况下，舱段存在较高的同轴度且具备较好的对接条件；而第3种情况下，只需要考虑装配孔销的位置匹配精度就能实现舱段的位姿匹配；第1和第2种情况下，由于在装配过程中两个对接舱段间每对装配孔销具备较高的同轴度，而不同的装配孔销的同轴度偏差要求不同。因装配孔销系中逐个确保轴线对合的偏差小，以及装配孔销在调整轴线方向时会导致其他装配孔销的轴线对合准确度不够，使其他装配孔销的同轴度偏差产生冗余。当舱段整体的同轴度高时，可以保证舱段对接面上装配孔销系的匹配误差小，即所有装配孔销的轴线方向偏差小。因此，对于舱段对接问题，首先应解决的是舱段的姿态方向估计的问题。

为了解决这个问题，本文通过采集舱段端面上的装配孔边缘图像来拟合二维椭圆信息，从而通过立体匹配方式获取孔的位置以及轴线方向，即孔的姿态方向，利用各个装配孔的姿态方向拟合出舱段的姿态方向，通过调整舱段整体姿态来保证装配孔销系姿态匹配的准确度。

2 装配孔的位姿解算

2.1 位姿参数标识

图1所示为基于双目视觉的大型舱段对接方式，无靶标的情况下，以舱段端面上的装配孔为特征点，实现舱段的对接。以左相机坐标系作为世界坐标系，本文视舱段端面上的装配孔以及舱段本身为互不影响的独立刚体。待测物的位姿可以用待测坐标系相对于世界坐标系的变换矩阵来表示，也可由圆心三维坐标 （x，y，z）T来表示位置，以及由姿态角 （α，β）T或姿态向量 （vx、vy、vz）T来表示姿态，若待测坐标系的0点为 （x，y，z）T，待测坐标系相对于世界坐标系OwXwYwZw的姿态角为 （α，β）T，其中待测坐标系中的下标type为坐标系的类型，H为装配孔，A为舱段，上标i为当type为H时，第i个装配孔的坐标系，α为俯仰角，β为偏航角。那么，装配孔与舱段作为待测物，其位姿均可以表示为其中，描述待测坐标系相对于世界坐标系的平移向量；描述待测物的位置，即装配孔和舱段端面的圆心位置。本文采用XYZ欧拉角以及ZA=（vxA，vyA，vzA）来描述舱段姿态，其中ZA为姿态方向单位矢量，可表示为

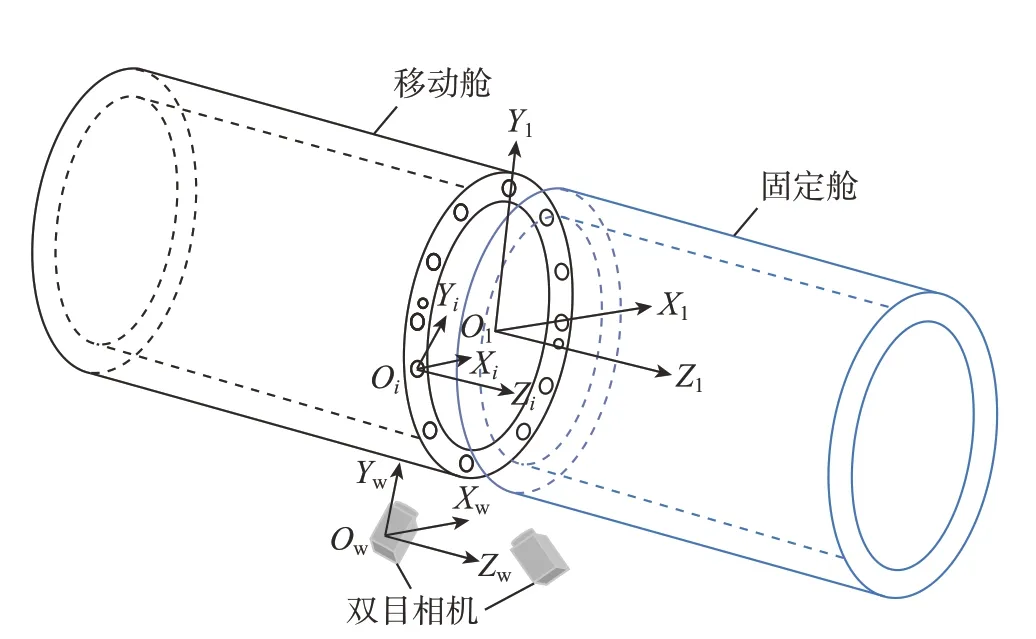
图1 舱段对接示意图Fig.1 Schematic diagram of cabin docking

2.2 装配孔的特征提取以及位姿求解

通过图2所示的双目视觉测量系统对孔进行位姿测量，利用双目视觉下形成椭圆锥模型来解算孔的位姿信息，即孔的圆心（x，y，z）T和姿态方向

图2 双目视觉测量系统Fig.2 Binocular vision measurement system

为保证获取到舱段端面上多个装配孔的位姿，可以设立多组双目视觉测量系统。利用射影几何的原理，建立双目椭圆锥体模型，如图3所示，进而求得装配孔的位姿。

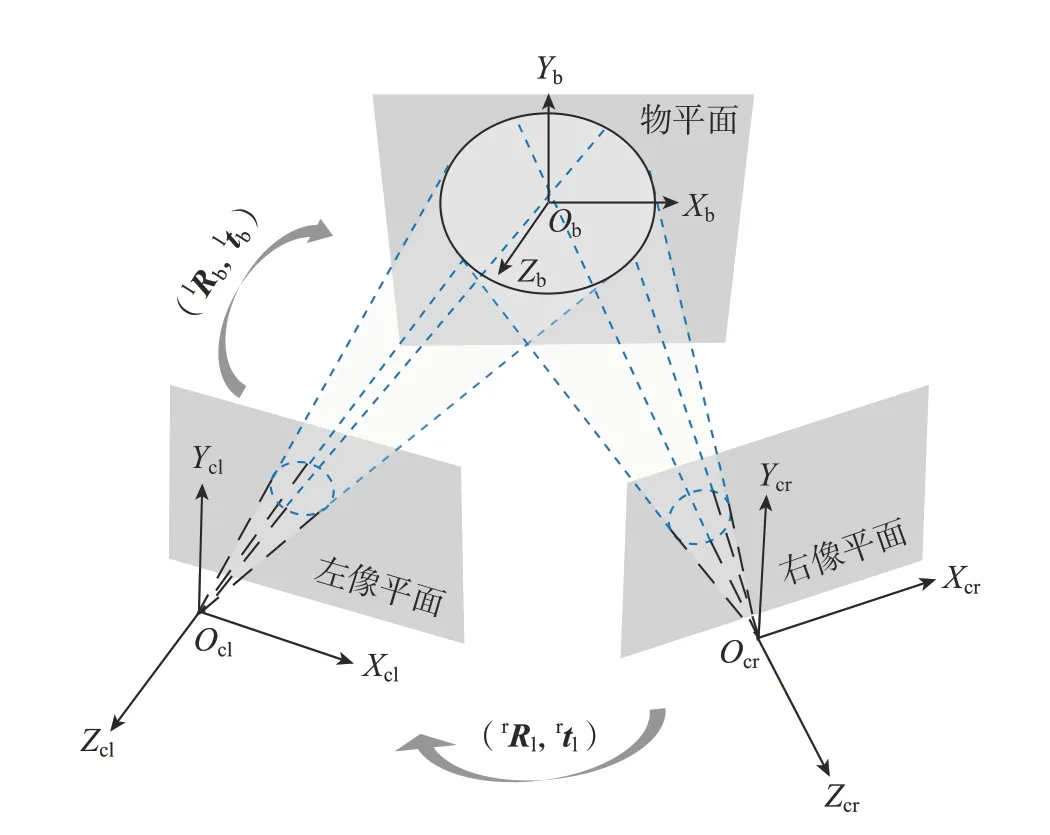
图3 双目椭圆锥面模型Fig.3 Binocular elliptical cone model

由于部分装配孔销 （如定位孔销）的轴线与孔面的垂直度较高，因此，通过获取装配孔的端面圆心以及端面法向量能够表示孔的轴线方向。获得装配孔的姿态信息，需要拟合出由双目视觉系统拍摄到的图像椭圆二维信息，在成像坐标系下椭圆表示为

用二次型表示为

因此，第i个装配孔对应的二维椭圆可以通过矢量表示Ellii=（Ai，Bi，Ci，Di，Ei，Fi）。为了获得矢量Ellii，需对图像进行预处理并提取一系列特征边缘像素点，通过这些像素点拟合椭圆。为了避免逐个处理像素点不能构成椭圆的情况发生，将像素点构成弧段进行批量处理，通过弧段匹配来达到像素点拟合椭圆的效果。因此，像素点pjk、弧段Arcij以及椭圆Ellii的关系为

式中，pjk[xjkyjk]T表示第j个弧段的第k个像素点。对图像进行预处理，通过双边滤波去噪以及Canny算子得到像素点pjk，再通过对LSD[11]轻量处理后提取弧段Arcij；以特征数和Pascal定理等射影不变量进行弧段匹配，构成弧段组系，即

式中，Wm={Arcm1，Arcm2，Arcm3，…，Arcmj}，m为弧段组的总数，可见Wm可以表示为一个椭圆，通过非迭代最小二乘法拟合出椭圆Ellim=（Am，Bm，Cm，Dm，Em，Fm），从而得到一组候选椭圆集。

候选椭圆集中存在重复以及虚假的椭圆，需将这些椭圆剔除。通过均值漂移聚类 （MeanShift）的方法实现椭圆去重。所谓虚假椭圆，指的是两个椭圆当中存在同一个弧段，故其中一个椭圆必定是假的。对虚假椭圆的剔除，本文采用Topsis熵权方法实现椭圆真假评估，首先，对弧段对应椭圆集进行归类，即

式（6）表示这些椭圆均包含了弧段Arcij；通过Topsis评价法来评估椭圆的真假性，首先设两个评估指标，分别为弧段Arcmj上像素点pjk落在椭圆Ellii上的比例µm及椭圆Ellim在边缘图上的重合率εm；通过熵权法来决定两个指标的权重v1、v2；计算Topsis的最佳距离和最差距离。

计算每个候选椭圆的评分

从每个弧段Arcmj对应的椭圆集{Ellimj}选出评分最高的椭圆，加入椭圆集Wfinal；对椭圆集Wfinal进行最后的筛选，保留存在同一弧段约束的评分高椭圆，最终得到的椭圆集{Elli1，Elli2，Elli3，…，Ellin}为舱段端面上的装配孔的二维椭圆信息集，其中n为装配孔的个数。

根据式（3）构建左右空间圆锥面方程。

式中，Ptype=（xtype，ytype，ztype）T，下标type为cl时表示在左相机坐标下的坐标，type为cr时表示在右坐标系下的坐标；Fl、Fr为左右相机的内参；Gli和Gri为第i个装配孔对应的椭圆二次型。令Ml=FlTGliFl和Mr=，用于表示左、右椭圆锥面的系数矩阵，将空间圆锥面方程转化到待测坐标系下。

其中，PHi为第i个装配孔所在的待测坐标系下的坐标；Qi为代表第i个装配孔在世界坐标系下的位姿；最终构建两个圆锥面相交形成的相贯线方程。

式中，ZiH的x分量为sinαcosβ，y分量为-sinβ，z分量为cosαsinβ，联立标准空间圆方程，求得装配孔的圆心位置

3 舱段姿态拟合模型建立

在舱段对接中，首要问题是确定舱段整体姿态方向，两个舱段姿态方向保持在同一个轴线后，在同轴方向上旋转舱段即可实现对合孔的匹配。从上一节内容中可以得到装配孔的位姿，其中包括位置和姿态，本文仅研究舱段姿态估计问题，通过装配孔系的姿态集来估计舱段整体姿态，为了方便分析，将装配孔的姿态方向采用单位矢量并以世界坐标系原点为起点，如图4所示，矢量（i=1，2，3，…，n）为装配孔在世界坐标系下的姿态方向。

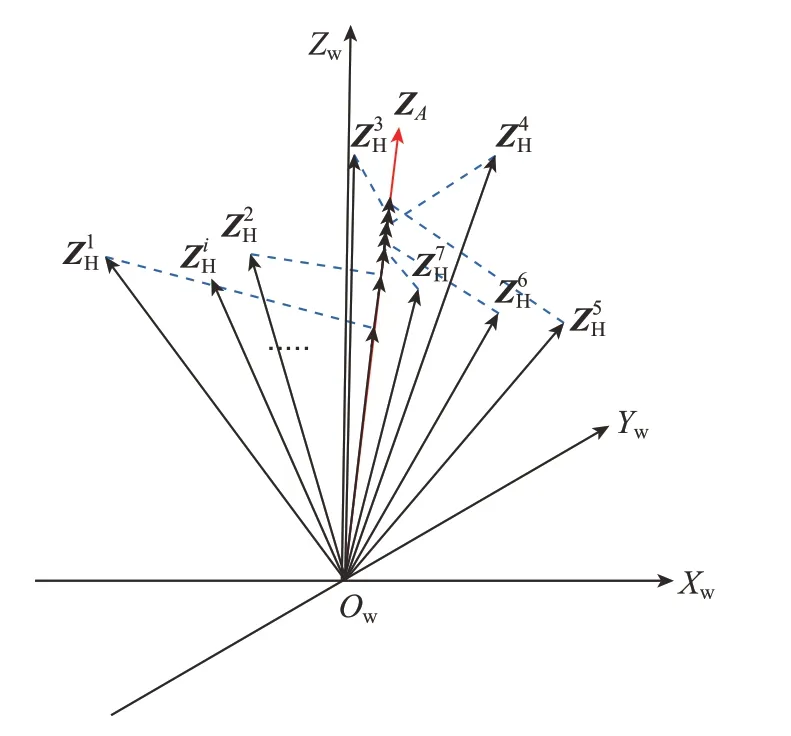
图4 最佳投影模型Fig.4 Optimal projection model

由于制造误差，加上每个装配孔的加工精度要求往往不同，导致孔的姿态与舱段端面姿态存在较小偏差，无法保证孔的姿态方向与舱段的姿态方向一致，故本文利用若干个装配孔来拟合舱段的姿态，采用投影寻踪的思想，将舱段姿态估计问题转化为求解最优的姿态方向ZA，使得装配孔的姿态方向ZiH投影在ZA上的模和长最大且拟合值ZA与理论值Zth的误差最小，则姿态估计问题的优化目标可表示为

式中，F（vxA，vyA，vzA）为装配孔投影在舱段的拟合姿态方向ZA（vxA，vyA，vzA）上的最大投影模长和；为第i个装配孔的姿态方向ZiH投影在舱段拟合姿态方向ZA的投影模长，其中，

式中，由于ZA与ZiH均设为单位矢量 （即|ZiH|=1、|ZA|=1），故

由于最佳投影方向具有聚集性，取值必定在所有待测装配孔姿态方向之间，因此，可以将F（vxA，vyA，vzA）描述为

式中，n为装配孔的个数，min （） 和max （） 分别代表自变量x和y的最小值和最大值。利用GA求解舱段姿态最优模型F（vxA，vyA，vzA），从而求得舱段的拟合姿态方向ZA。

下一步求拟合值ZA和理论值Zth之间的误差，本文利用欧氏距离来计算ZA和Zth的三维矢量方向的偏差，即

4 遗传算法求解模型

GA是一个全局搜索最优解的智能算法，通过模拟生物遗传进化的过程来得到最优值，其主要步骤包括编码、交叉变异、选择等操作。

4.1 种群初始化

本文采用实数编码对自变量基因vxA、vyA、vzA进行编码，最佳投影向量必定会在所有螺丝钉法向量的取值范围内，即

式中，rands为[-1，1]之间的随机数；rand为[0，1]之间的随机数。

由于3个染色体之间存在等式约束，即vx2A++vz2A=1，故对上述编码进一步优化，故

该优化模型为最大值问题，是建立在求得的最佳投影向量为单位向量的基础上，当种群中某个体的目标函数值对应的向量的模大于或小于1时，该目标函数值是不可行的，为了确保算法求得解的精度更高，引入罚函数法进一步约束处理，即

式中，e为惩罚度；M为惩罚因子，默认值为1。

程序会随机生成N个初始编码染色体，即N个初始种群个体，均满足优化函数中的所有约束。

4.2 种群个体适应度的设置

种群个体适应度对于求解最优值十分重要，它决定了种群个体遗传给下一代的概率。求最佳投影的优化函数为非线性求模和最大的问题，则适应度函数可为

式中，maxF为fit（F（vxA，vyA，vzA））的最大估计值。

4.3 种群进化过程

本文采用单点交叉的方式对两个配对的染色体交换部分基因，进而形成两个新的个体，之后按照一定的变异概率对染色体变异，变异是必不可少的一步，可以加强GA的局部优化的能力，再通过一对一置换机制进行父子选择，存在下面4种情况：（1）当父子代的惩罚度均小于10-15且子代的适应度比父代适应度好的时候才替换掉，即fit（a）＞fit（b），选择个体b； （2）当父代的惩罚度小于10-15而子代的惩罚度大于10-15时，选择父代； （3）当子代的惩罚度小于10-15而父代的惩罚度大于10-15时，选择子代； （4）当父子代均大于10-15时，选择适应度好的个体，即若fit（a） ＞fit（b），选择个体b，若fit（b）＞fit（a），选择个体a。采用这种选择方式是为了保证群体的多样性，最后计算新种群的目标函数的值，重复进行整个遗传过程直到迭代结束。

5 试验与分析

为了验证算法的有效性，对实际舱段对接建立结构模型，如图5所示，轴1与轴2存在一定的角度偏差，在这种情况下研究舱段姿态估计问题。本试验对结构模型右侧舱段作1∶1的实体还原，搭建了双目视觉测量系统试验平台，主要包括试验舱段模型以及两个CCD相机、位姿调整平台，如图6所示，主要采集试验舱段上的2个定位孔以及12个装配孔。

图5 结构对接模型Fig.5 Structural docking model

图6 测量试验平台Fig.6 Measurement test platform

通过双目测量系统测量出每个孔的姿态方向，本文仅讨论舱段在小距离范围内的偏转，即姿态角∝∈[-3°，3°]，根据试验舱段的尺寸大小以及千分尺的精度要求，位姿调整平台选择千分尺进给，符合试验测量精度，进给量为43″/刻度，初始位置为0°，沿Y轴每进给50刻度即0.5790°，对舱段模型采集一次图像，总共采集了11帧图像。在MATLAB环境下使用GA算法进行计算，取种群个数size=200，迭代次数N=100，变异概率p=1/3。

对其中一帧图像建立姿态优化模型并通过MATLAB进行仿真处理，图7呈现了优化函数在约束下的有界光滑曲面切片，其中颜色表示F（vx，vy，vz）的值，表示舱段上装配孔系的单位姿态向量的模长和，当F逐渐趋近于理想值时，在约束范围内会收敛于某一姿态 （vx，vy，vz），故最佳投影模型存在最优解且具有唯一性。

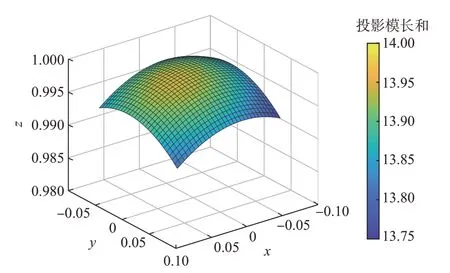
图7 优化模型切片图Fig.7 Optimized model slice plot

观察图8可以看出，GA算法最终都会收敛，逐步趋近于理想值，会在13.90左右停止。曲线上出现大于理想值的峰值，峰值所表示的姿态方向的模大于1，不满足最大值的要求。

图8 GA迭代结果Fig.8 GA iteration results

为了验证算法的正确性，本文将拟合出的舱段姿态方向与理论姿态方向进行对比分析，对比结果如表1所示，从试验结果可以看出，本方法拟合出的舱段姿态方向与理论姿态方向的姿态偏差最大不超过0.00903，平均误差为0.0048。拟合出一个姿态结果平均用时为0.782 s。拟合值ZA和理论值Zth的欧氏距离进行误差分析，如图9所示，最大误差不超过0.00045，平均误差为0.00008。

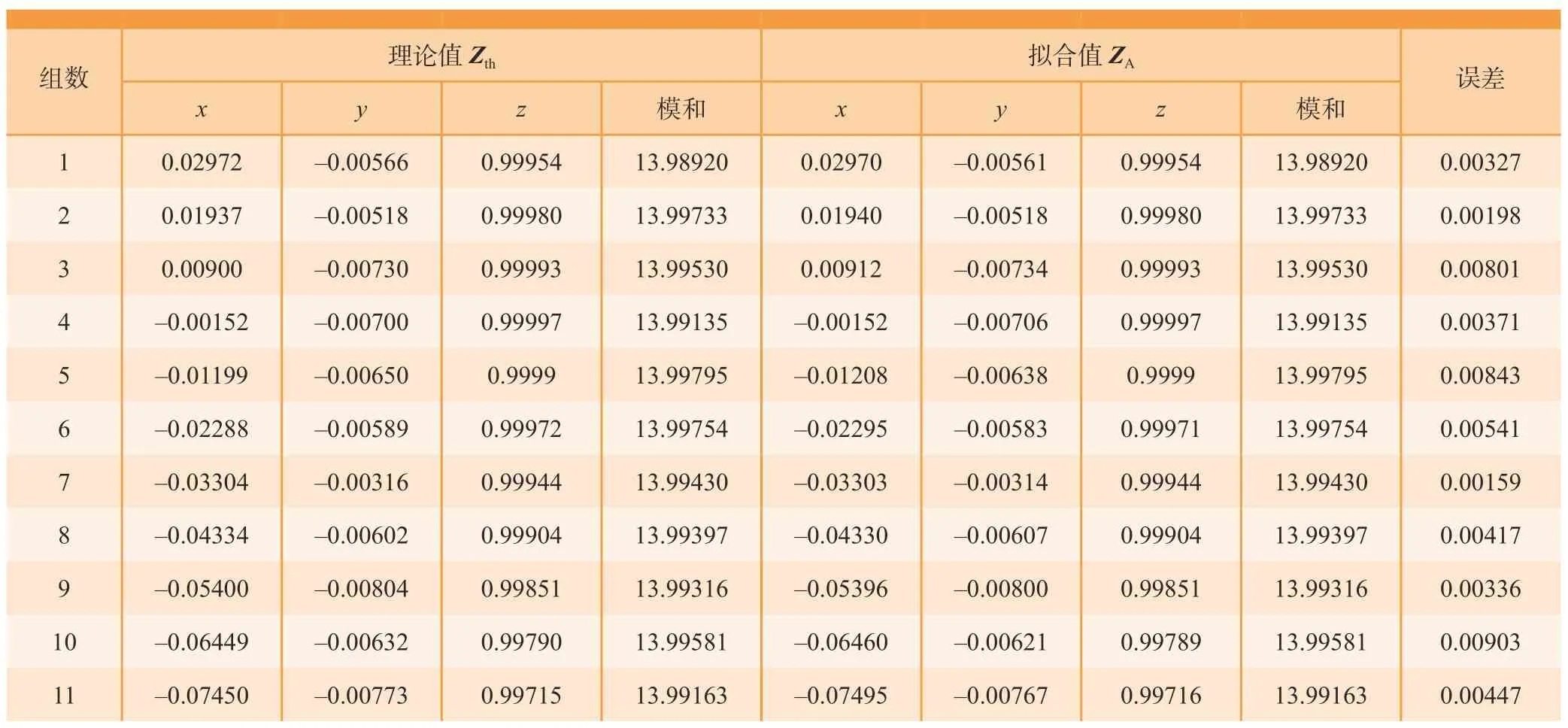
表1 姿态的理论值、拟合值以及误差Table 1 Theoretical values and fitted values of attitudes and erors

图9 拟合值与理论值的欧氏距离Fig.9 Euclidean distances of fitted values and theoetical values

已采集的11帧图像通过本算法计算得到姿态角，以姿态调整平台调整的姿态角为真实值，进行对比并精度评价。表2中的帧数序号1～11分别表示从幅值不断增加所对应的固定姿态的测量参数以及真实值的对比。随幅值变化，姿态角绝对误差变化曲线如图10所示，仿真曲线表明，随着幅值逐渐减小，绝对误差呈现减小趋势，这是因为舱段端面逐渐进入左相机的最佳视场角，定位精度相对高。本算法求得姿态角的绝对误差均值为0.0115°，绝对误差不超过0.0265°，相对误差为1.92%，满足姿态测量的精度要求。随着幅值增大，求解精度影响较小，姿态误差浮动在很小的范围内。

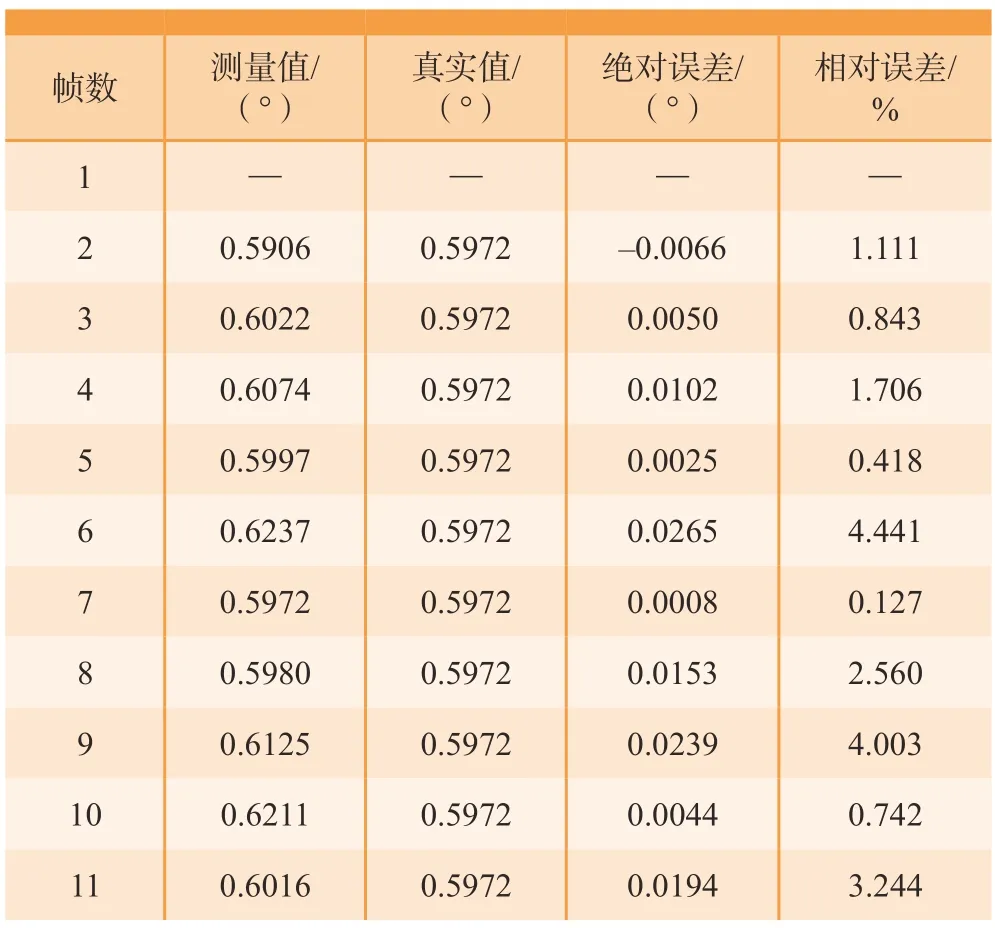
表2 姿态角测量结果Table 2 Measurement results of attitude angles

图10 姿态角绝对误差Fig.10 Errors of attitude angle

11帧图像采集均沿着Y轴方向，表示当幅值不断增加时，姿态满足线性变化，通过MATLAB进行姿态仿真，如图11所示，姿态变化呈线性分布。

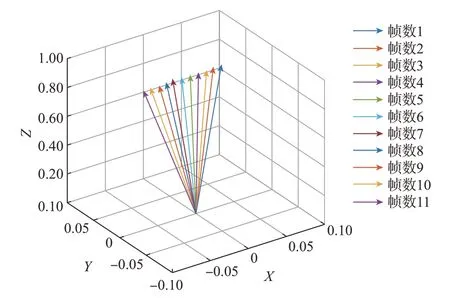
图11 姿态变化分布Fig.11 Attitude change distribution

为更好说明提出方法的有效性，分别沿着位姿调整平台的X轴、Z轴方向每移动1 mm采集一次图像，共采集5帧图像，同样，以调整平台移动的相对姿态作为真实值，与本算法计算的位姿进行对比并分析。由于调整平台的姿态角不发生调整，姿态保持不变。测量结果如表3和4所示。

表3 沿X轴的测量结果Table 3 Measurements along the X-axis

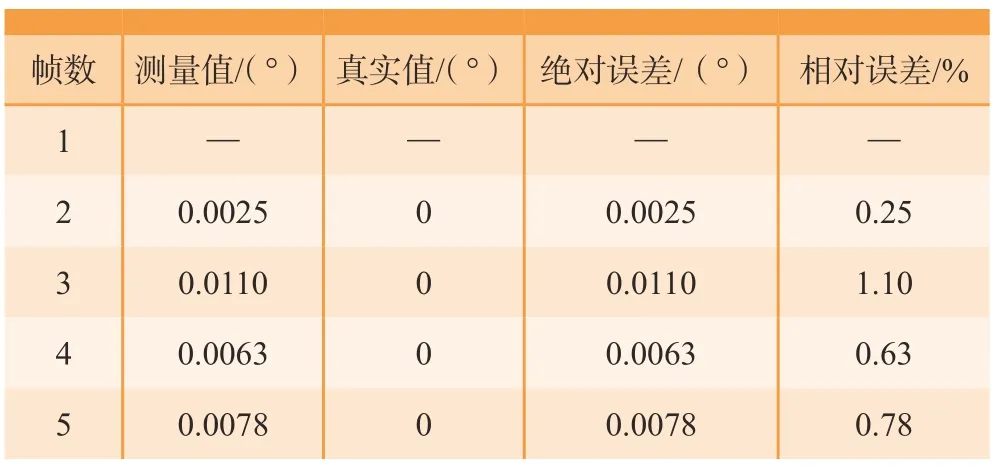
表4 沿Z轴的测量结果Table 4 Measurements along the Z-axis

从表3和4中可以看出，沿X轴平移的姿态角误差不超过0.0186°，绝对误差平均值为0.0089°，相对误差平均值为0.89%；沿Z轴平移的姿态角误差不超过0.0110°，绝对误差平均值为0.0069°，相对误差平均值为0.69%。在平移方向上相对姿态的误差均不超过1%，说明本方法的解算位姿的精度较高。

6 总体框架

本文通过双目视觉测量系统获取装配孔的位姿。双目视觉测量的框架如图12所示，主要分为椭圆特征提取、特征孔位姿测量以及舱段姿态拟合3个功能模块。

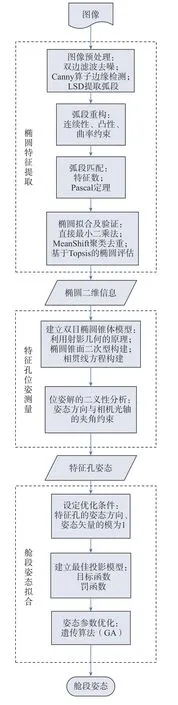
图12 双目视觉测量框架Fig.12 Binocular vision measurement framework

（1）椭圆特征提取。首先对双目相机进行标定，获取相机的内外参数，相机采集舱段上的装配孔图像，之后对图像进行处理。主要对图像去噪以及边缘检测等预处理，提取弧段并进行弧段匹配，根据最终的弧段组拟合椭圆，从而经过一系列的去伪工作后获得装配孔的二维信息。

（2）特征孔位姿测量。利用射影几何的原理，建立双目椭圆锥体模型，实现二维椭圆信息向三维空间转换，得到装配孔的空间三维位姿信息，该模型得到的位姿解存在二义性，通过光轴与实际装配孔的姿态方向的约束消除二义性，得到最终的姿态解。

（3）根据若干个装配孔的姿态方向存在公共投影向量的特点，建立数学优化模型，通过GA求解模型的最优解，从而求得舱段的姿态方向。

7 结论

本文针对大型舱段的整体姿态测量问题，提出了基于最佳投影的多孔拟合舱段姿态的方法。

（1）通过双目测量系统求得舱段上装配孔姿态的前提下进行讨论，并将所有姿态方向进行单位化。建立最佳投影方向数学模型，采用GA来求得该数学模型的最优解，拟合出的舱段最优姿态与装配孔姿态的残差最小。

（2）以试验舱段模具为例，进行多组对比试验，经过对比分析验证了本文方法的可行性，姿态角偏差的绝对误差为1.92%，满足姿态测量的精度要求。

（3）本文方法可以有效解决导弹、航天器等大型舱段产品的对接装配中姿态调整的问题，具有远大的应用前景。